Categorical data Norminal scale Ordinal scale Continuous data








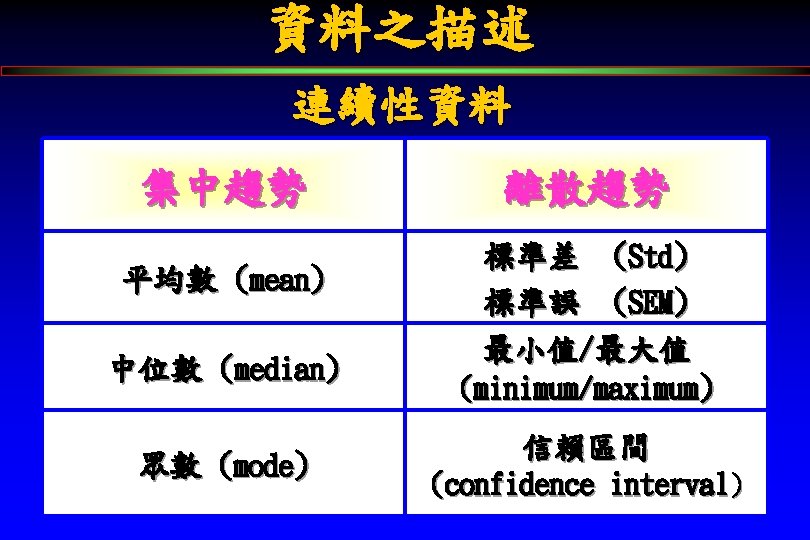





















- Slides: 57









資料之屬性 分類資料(Categorical data) 類別尺度(Norminal scale) 序位尺度(Ordinal scale ) 連續資料(Continuous data) 等距尺度(Interval scale) 比率尺度(Ratio scale )









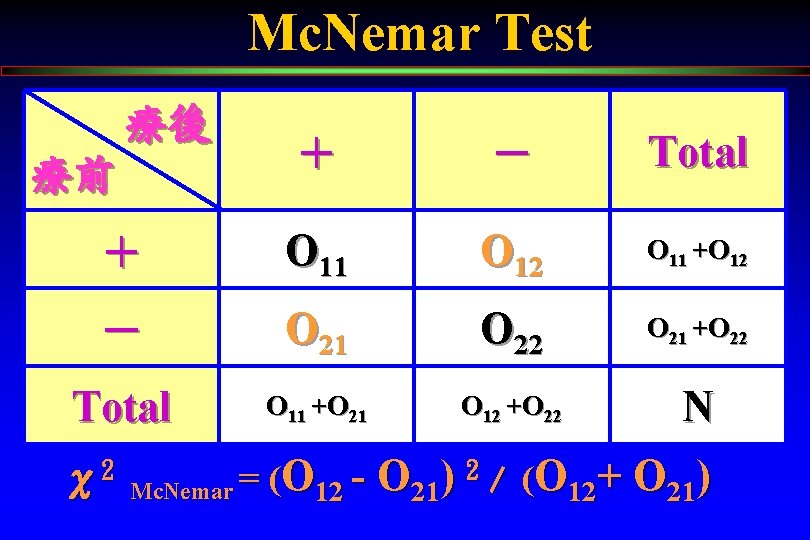
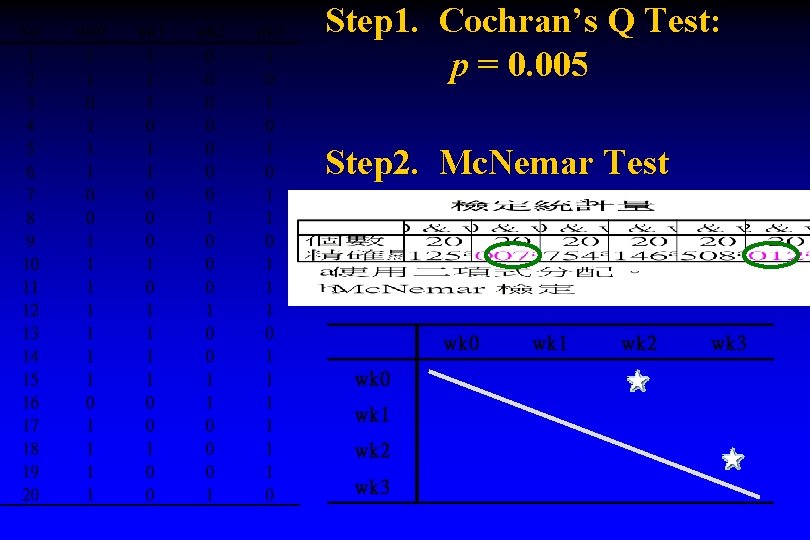
Mc. Nemar Test 療後 + - Total + O 11 O 12 O 11 +O 12 - O 21 O 22 O 21 +O 22 Total O 11 +O 21 O 12 +O 22 N 療前 χ2 2 / (O + O ) = ( O O ) Mc. Nemar 12 21

Step 1. Cochran’s Q Test: p = 0. 005 Step 2. Mc. Nemar Test

類別性資料之檢定(二) 兩組類別變數( 2 × 2 Table) Fisher’s exact test (Expectation<5) Yate’s correction of contingency (Expectation>5) 三組以上類別變數( m ×n Table m, n≧ 2) Pearson Chi-Square test 血型類型是否因性別不同而有差異

2 χ 疾病 變數 + Test - Total + O 11(E 11) O 12 (E 12) a - O 21 (E 21) O 22 (E 22) b Total χ2 (1) = c d N 2 / (E ) 〕 〔 ( O – E ) ij ij

2 χ Test 觀察值( Oij ) O 11 , O 12 , O 21 , O 22 期望值( Expectation: E ij ) E 11 = ( a × c ) / N E 12 = ( a × d ) / N E 21 = ( c × b ) / N E 22 = ( d × b ) / N

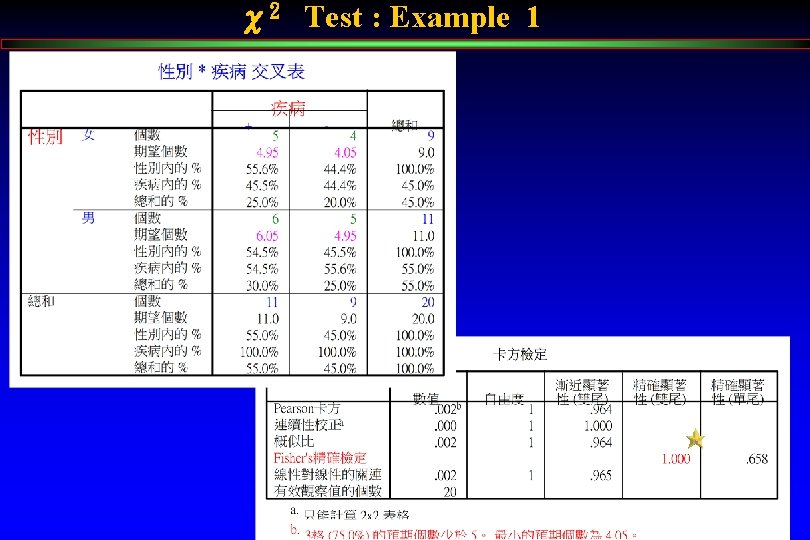
χ2 Test : Example 1

χ2 Test : Example 2

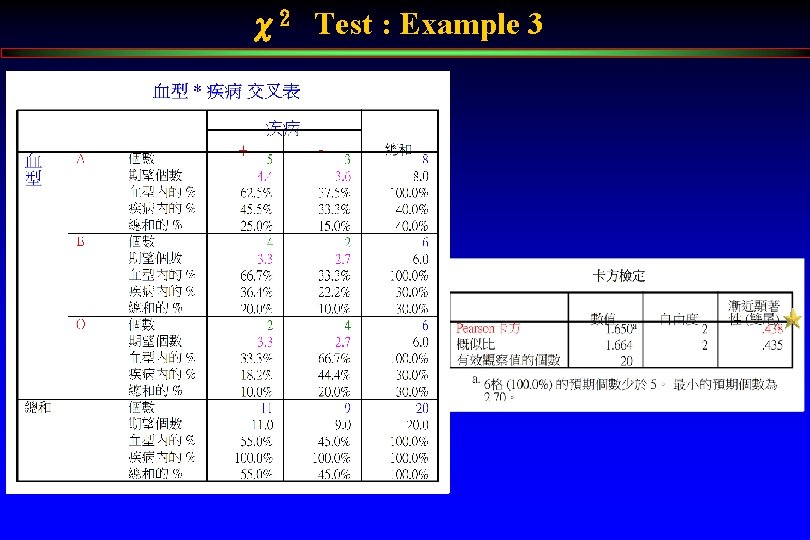
χ2 Test : Example 3


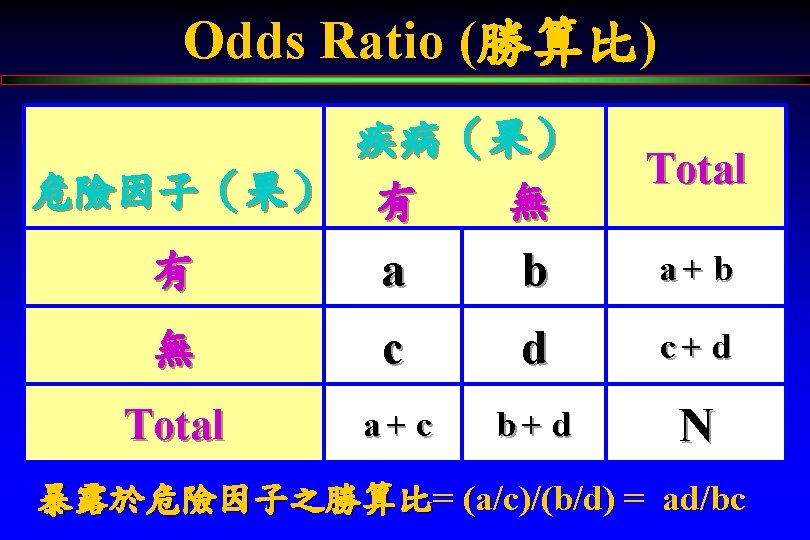
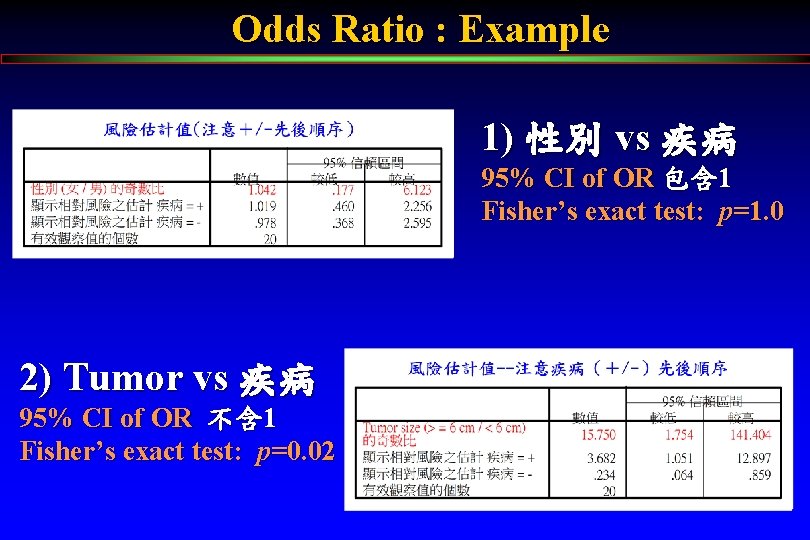
Odds Ratio : Example 1) 性別 vs 疾病 95% CI of OR 包含 1 Fisher’s exact test: p=1. 0 2) Tumor vs 疾病 95% CI of OR 不含 1 Fisher’s exact test: p=0. 02

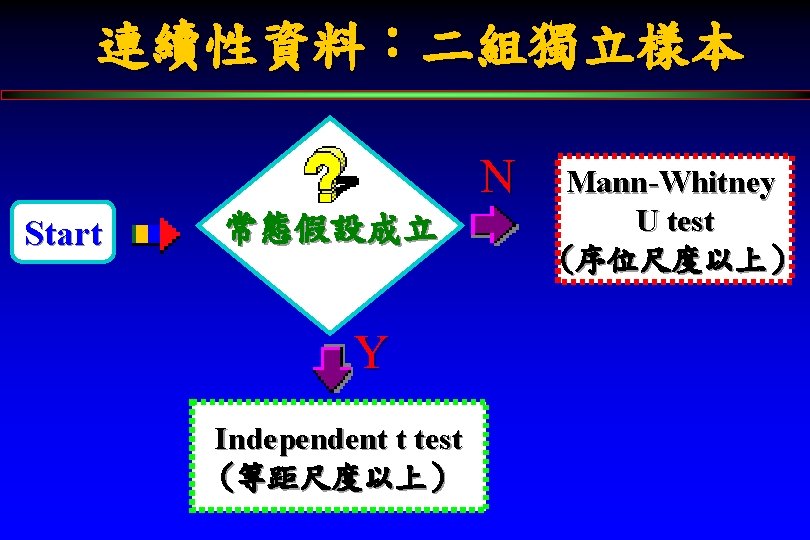
連續性資料之檢定(一) 二組獨立樣本資料 Independent t test (Parametric test) Mann-Whitney U test (Nonparametric test) 三組以上獨立樣本 ANOVA (One-way, Two-way) Kruskal-Wallis test (Nonparametric test )

連續性資料之檢定(二) 成對/二組相關樣本資料 Paired t test (Parametric test) Wilcoxon Signed-Rank test (Nonparametric test) 三組以上相關樣本 ANOVA (單因子重複量數變異數分析) Friedman test (Nonparametric test )

Post-Hoc Comparison ( 事後檢定 ) LSD (最小顯著差距) Scheffe Bonferroni Tukey 聯合信賴區間 H 0: μ 1=μ 2=…=μk




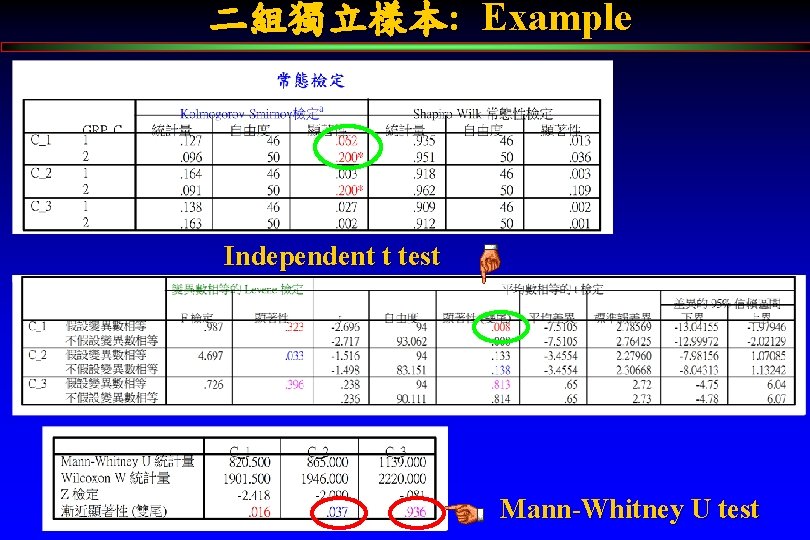
二組獨立樣本: Example Independent t test Mann-Whitney U test

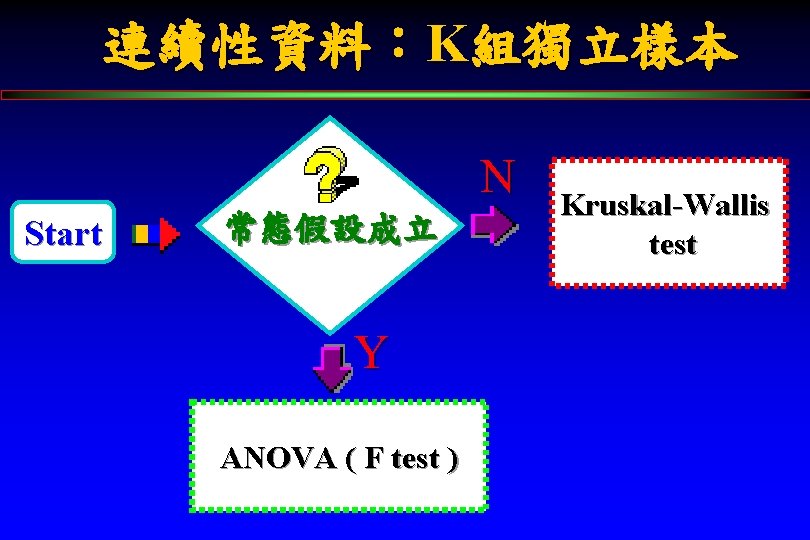
連續性資料:K組獨立樣本 N Start 常態假設成立 Y ANOVA ( F test ) Kruskal-Wallis test

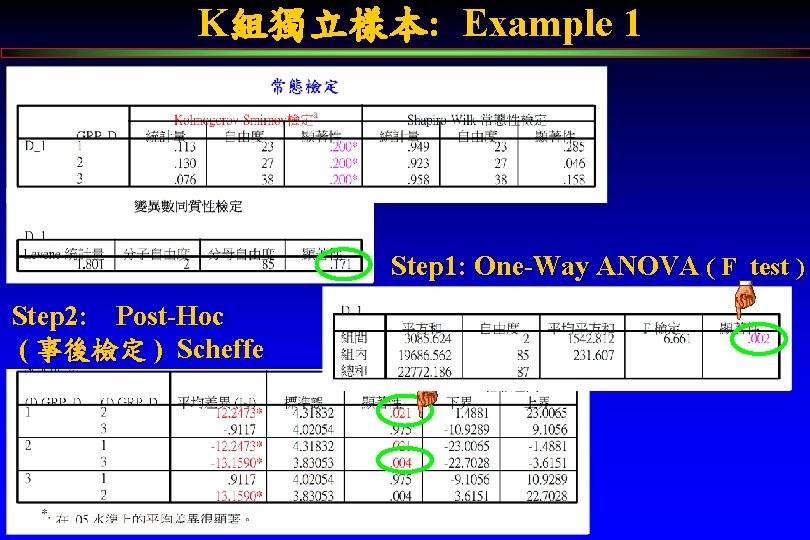
K組獨立樣本: Example 1 變異數同質性檢定 Step 1: One-Way ANOVA ( F test ) Step 2: Post-Hoc ( 事後檢定 ) Scheffe

K組獨立樣本: Example 2 Step 1: Kruskal-Wallis test Step 2: Post-Hoc Mann-Whitney U test

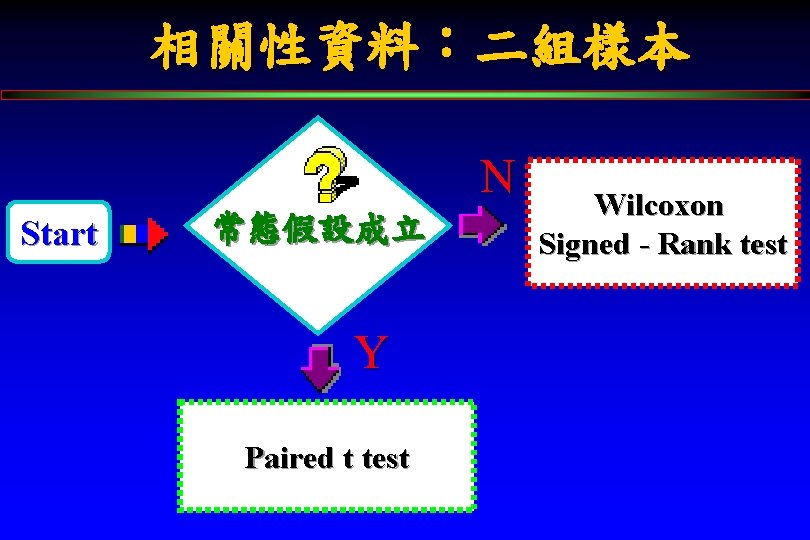
相關性資料:二組樣本 N Start 常態假設成立 Y Paired t test Wilcoxon Signed - Rank test

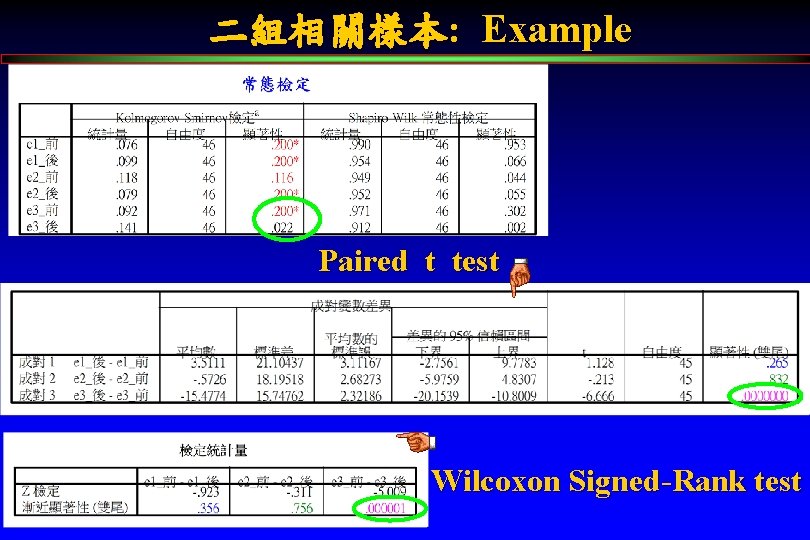
二組相關樣本: Example Paired t test Wilcoxon Signed-Rank test

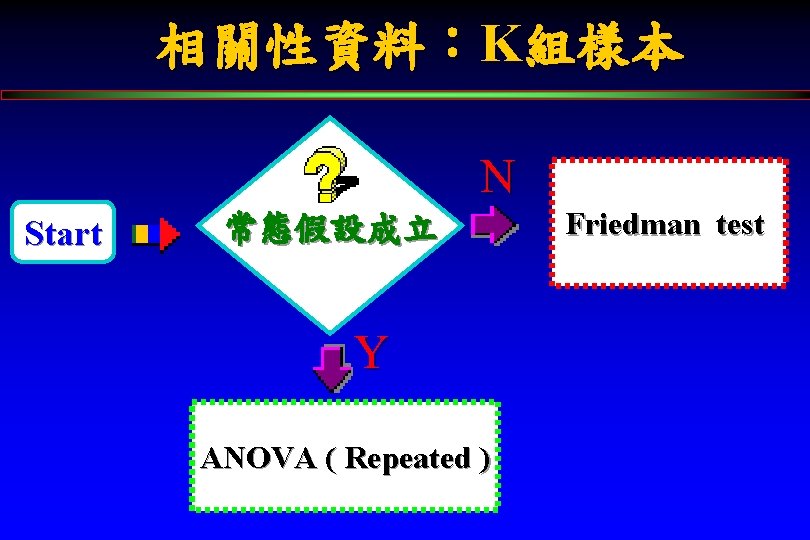
相關性資料:K組樣本 N Start 常態假設成立 Y ANOVA ( Repeated ) Friedman test

K組相關樣本: Example I Step 1: Friedman test Step 2: Post Hoc Wilcoxon Signed-Rank test

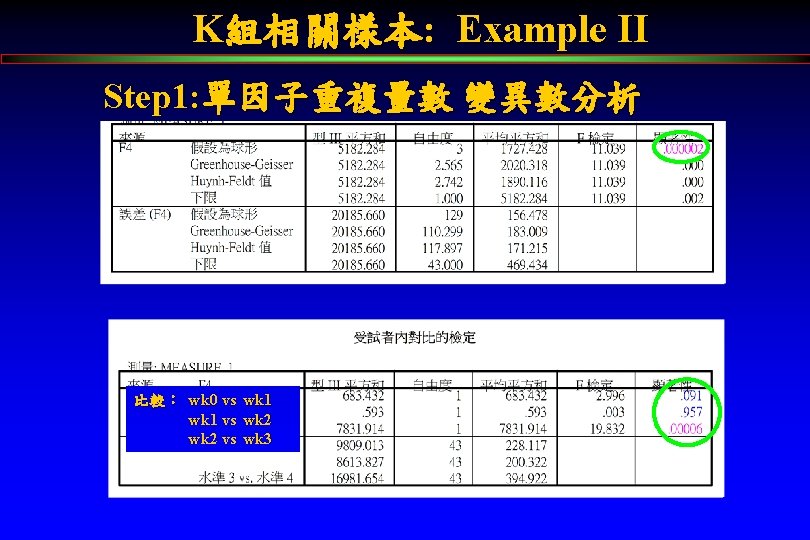
K組相關樣本: Example II Step 1: 單因子重複量數 變異數分析 比較: wk 0 vs wk 1 vs wk 2 vs wk 1 wk 2 wk 3



Linear Regression vs Logistic Regression 比較 Multiple Regression 因變數 Y必須為連續性資料 自變數 注意 事項 可為連續性或類別資料需以虛擬變數 表示(Dummy variable) K個水準的類別資料需設 K-1個虛擬自變數 Ex: 性別(0/1) 1個 血型(A/B/O/AB) 3個 x 1 x 2 x 3 A: ( 0 0 0 ) B: ( 1 0 0 ) O: ( 0 1 0 ) AB: ( 0 0 1 ) Logistic Regression Y必須為類別性資料(是/否) 可為連續性或類別資料需設定參考組 Odds Ratio 95% CI of Odds Ratio P value (Wald statistic) Accuracy of model=85. 9% Nagelkerke R 2

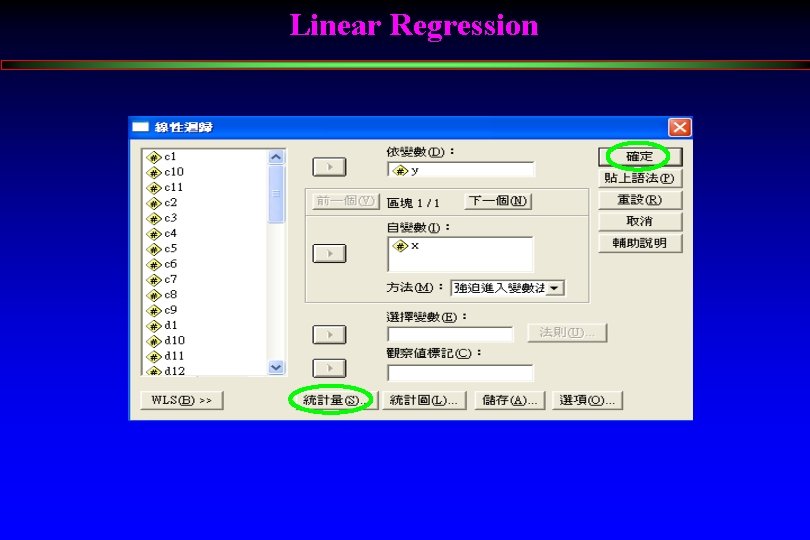
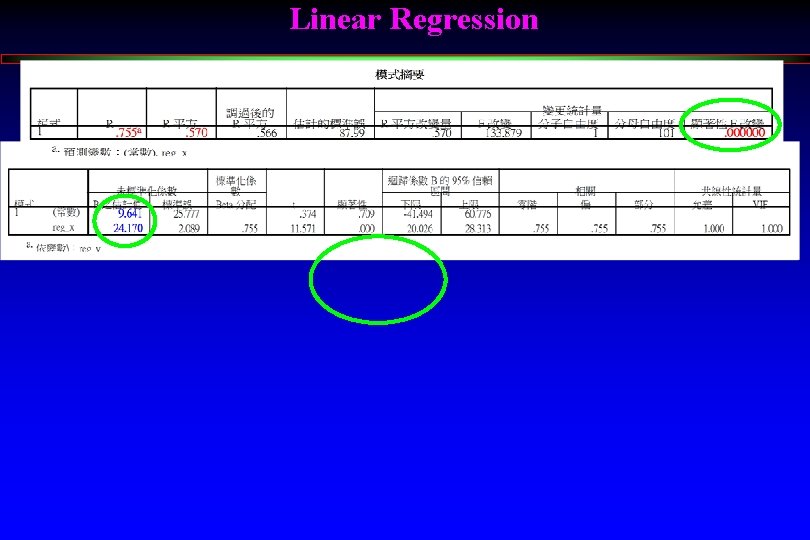
Linear Regression

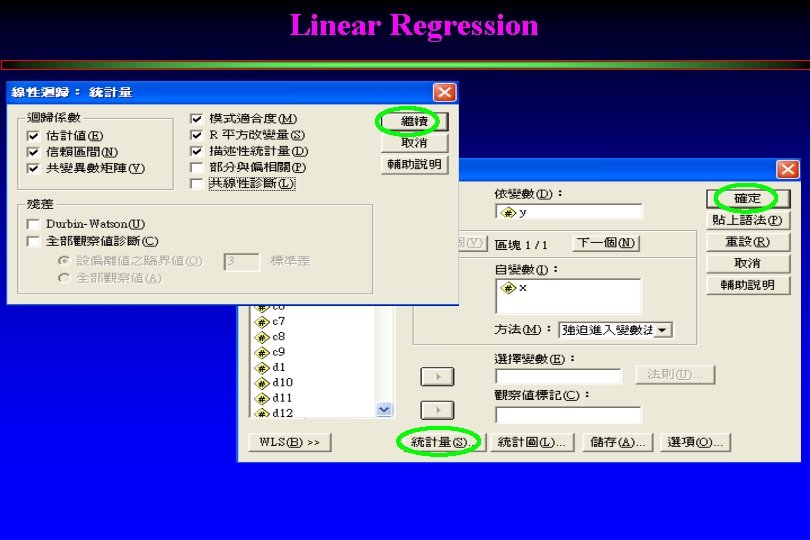
Linear Regression

Linear Regression

Linear Regression

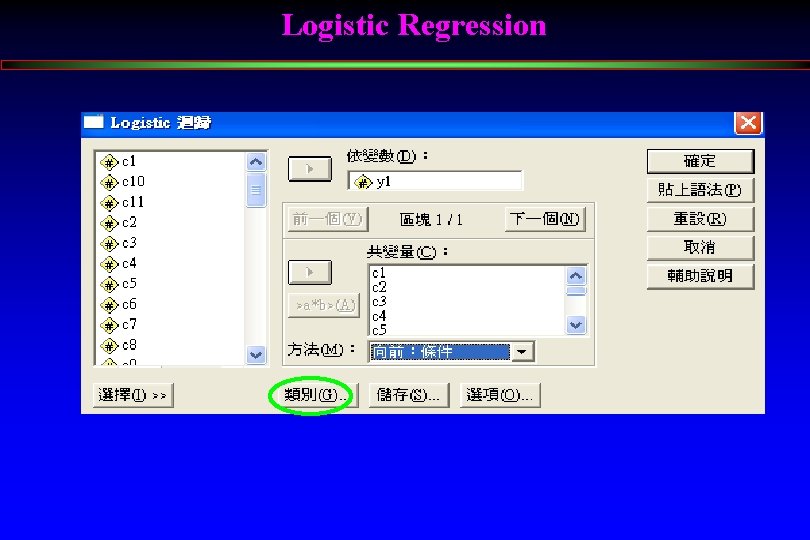
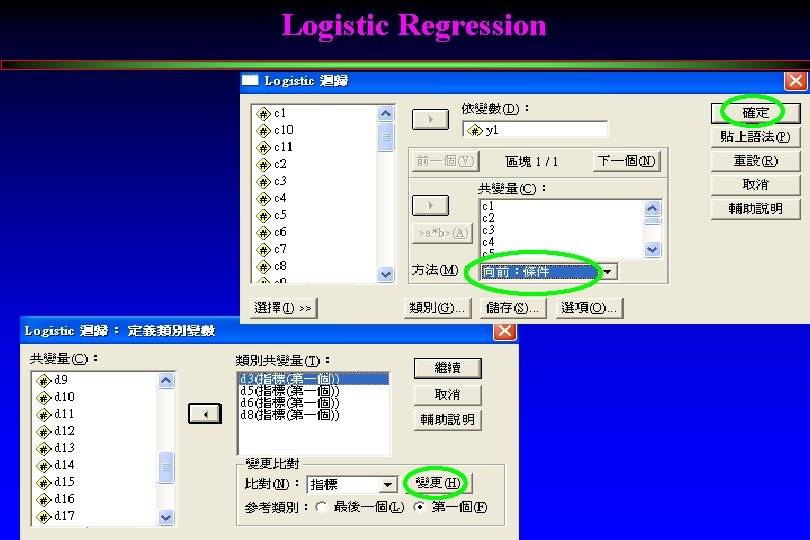
Logistic Regression

Logistic Regression

Logistic Regression

Logistic Regression

Logistic Regression

Logistic Regression

其他常用之統計分析法 信度分析 Logistic Regression 單變量/多變量線性迴歸 Kaplan-Meier Survival analysis Cox proportional-harzard model

Thank You For Your Attention !