CASLCommon Algebraic Specification Language Anis Yousefi Ph D

CASL-Common Algebraic Specification Language Anis Yousefi Ph. D. Candidate Department of Computing & Software Mc. Master University yousea 2@mcmaster. ca

Outline o Introduction o CASL’s Basic Specifications o CASL’s Structured Specifications o CASL’s Architectural Specifications o Tools & Case Study 2

The Common Algebraic Specification Language o Common n n o Co. FI: the international common framework initiative Designed to replace existing algebraic languages and provide a standard Algebraic Specification n Programs as algebraic structures Data Values + Functions Specification in terms of axiom 3

CASL Layers o Basic (Unstructured) Specifications n o Structured Specifications n o Naming, Parameterization, etc. Architectural Specifications n o Specifications in terms of signatures and sentences Reusable implementation units Libraries of named specifications 4

Basic Specifications o Declaration of symbols + set of axioms and constraints (restricting the interpretations of the declared symbols) Σ Class of Σ-Models satisfy o M ╞═ SP Symbols Interpretations of Σ which the axioms and constraints of the specifications : “Model M satisfies specification SP” or “M is a model of SP” 5

Specifications and Institutions o o To develop concepts of a spec language independent of the underlying logical system I = (Sign, Sen, Mod, ╞═) n n n Sign: category of signatures Sen: set of sentences for each signature Senσ : sentence translation map Mod: category of models for each signature Modσ : model reduction functor ╞═ : satisfaction relations for each signature (whether a sentence holds in a model or not) 6

Notations o o o o Σ = (S, F) σ : Σ Σ’ Sign: category of signatures Sen(Σ): set of sentences for signature Σ Senσ : Sen(Σ) Sen(Σ’) Mod(Σ): set of models for signature Σ Modσ : Mod(Σ’) Mod(Σ) ╞═Σ |Mod(Σ)| Sen(Σ) 7

Discussion on signatures o o o Signatures define (non-logical) symbols used in sentences & interpreted in models Signature Morphisms allow to extend signatures, change notations, … Signature Morphisms lead to translation of sentences & models such that satisfaction is preserved 8

Logic o o o Institutions + Entailment System Extending institutions with proof-theoretic entailment relations compatible with semantic entailment LOG = (Sign, Sen, Mod, ╞═, ├─) ├─ Σ P(Sen(Σ)) Sen(Σ) (derivation rules) o Soundness: if Γ├─Σ φ then Γ╞═Σ φ o Completeness: if Γ╞═Σ φ then Γ├─Σ φ 9

CASL’s Basic Specifications o o Adds sub-sorting, partiality, first order logic & induction To add sub-sorts n n Many-sorted institutions with partial functions, FOL, sort generation constraints Constructing sub-sorted institutions from manysorted institutions 10

Many-Sorted Institutions o I = (Sign, Sen, Mod, ╞═) n n n Sign: category of many-sorted signatures Sen: set of many-sorted sentences for each signature Senσ : sentence translation map Mod: category of many-sorted models for each signature Modσ : model reduction functor ╞═ : satisfaction relation for each signature 11

Many-Sorted Signature o Σ = (S, TF, P) n n o S: set of sorts TF: total function symbols PF: partial function symbols P: predicates Signature Morphism 12

Many-Sorted Σ-Models o M = (MS, TFM, PM) n MS: a family of non-empty carrier sets indexed by sort s in S, for each sort in Σ n TFM: Mw Ms , for each TF in Σ Mw: Cartesian product of Ms for sorts in the domain of TF n PFM: Mw ? Ms , for each PF in Σ n PM Mw , for each P in Σ 13

Many-Sorted Σ-Sentences o o o Closed many-sorted first-order formulae (no variables) Sort generation constraint over Σ Σ X T Many-Sorted Atomic ΣFormulae Many-Sorted First-Order Formulae n Variables X over Σ n Terms T: X + applications of Σ-functions over X 14

Many-Sorted First-Order Formulae o o Many-Sorted Atomic Σ-Formulae n Application of a predicate symbol to terms n Existential equation n Strong equation n Assertion def t: defining value of term t Many-Sorted First-Order Formulae n Add formula “false” and closing under implication and universal quantification 15

Sort Generation Constraint Over Σ o A given set of sorts is generated by a given set of functions o Along with a signature morphism that allows translation o o ({nat}, {0; suc}, id) 16

Satisfaction of sentences o o o P(t 1, …, tn) is satisfied if the value of t 1 to tn is defined and give a tuple belonging to PM “def t” is satisfied if the value of t is defined is satisfied if values of t 1 and t 2 are defined and equal or both values are undefined A sort-generation constraint is satisfied if the carriers of the sorts in are generated by the function symbols in from the values in the carriers ╞═ ╞═ of sorts not in. Then 17

Entailment System o Rules of derivation 18

Soundness and Completeness o Soundness: n o CASL institutions equipped with the provided entailment system is sound Completeness: n it is complete if sort generation constraints are not used. 19

Sub-Sorting in CASL o o Injective embedding between carriers (not necessarily as inclusions) Allows for more general models in which values of a sub-sort and super-sort are represented differently n Integers (represented as 32 -bit words) and Reals (represented using floating-point representation) 20

Sub-sorted Institutions o o o A category of sub-sorted signatures is defined A functor from this category into the category of many-sorted signatures is defined The notations of models, sentences, and satisfaction is borrowed from the manysorted institutions via this functor 21

Sub-sorted Signature o o Σ = (S, TF, P, ≤) ≤: reflexive and transitive relation on set of sorts Sub-sorted signature morphism: manysorted signature morphism that preserves “≤” and “overloading relations” between functions Overloading relation n n Shared sub-sort in their domain Shared super-sort in their range 22

Constructing Sub-Sorted Signatures from Many-Sorted Signatures s s’ o o em: embedding o pr: projection o o em pr in: membership predicate for each pair of sorts s ≤ s’ Construction ^ is a functor from category of sub-sorted signatures into the category of many-sorted signatures 23

Sub-Sorted Models o Many-sorted models satisfying some axioms n n n n Embedding functions are injective. The embedding of a sort into itself is the identity function. All compositions of embedding functions between the same two sorts are equal functions. Projection functions are injective when defined. Embedding followed by projection is identity. Membership in a sub-sort holds just when the projection to the sub-sort is defined. Embedding is compatible with those functions and predicates that are in the overloading relations. 24

Sub-Sorted Sentences o o Sub-sorted Σ-sentences are ordinary manysorted sentences for Translation of sentences along a sub-sorted signature morphism σ is ordinary manysorted translation along 25

Satisfaction and proofs o o Reuse satisfaction conditions from manysorted Proof calculus can borrowed from the many -sorted case Φ├─Σφ o Φ U Ax(Σ)├─^Σφ Soundness and completeness follow from the many-sorted case 26

Structured Specifications o 27

Structured Specifications o o o SPEC 1 and SPEC 2 (Union): Combines specifications (re-use) SPEC 1 with Symbol Mapping (Translation) : Renaming of symbols SPEC 1 hide Symbol List (Reduction): Hiding symbols SPEC 1 Then SPEC 2 (Extension): Enriching models by declaring new symbols and asserting their properties and/or specializing the interpretation of already declared symbols Free {SPEC}: Restricting to free data-types 28

Naming, Parameterization, & Views o o o Name to refer to the specification Generic specifications: parameters Instantiation: providing an argument for each parameter + a fitting morphism from the parameter to the argument Fitting may also be achieved by use of named views between the parameter and argument specifications view VN : SP to SP’ = Symbol Mapping o 29
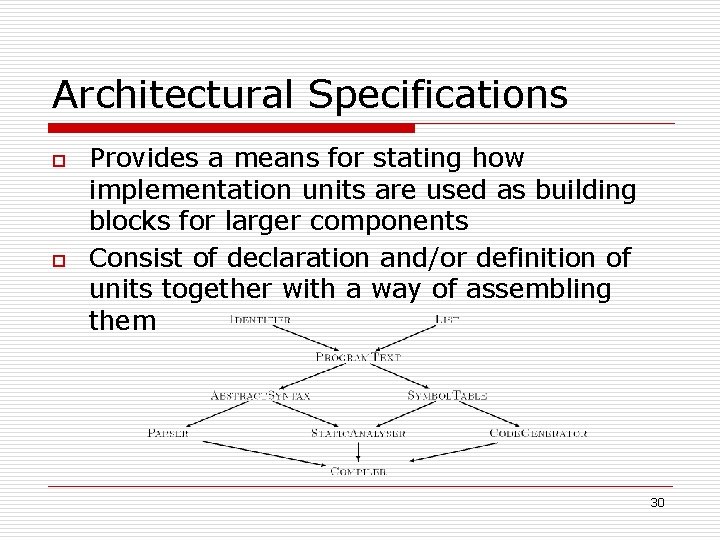
Architectural Specifications o o Provides a means for stating how implementation units are used as building blocks for larger components Consist of declaration and/or definition of units together with a way of assembling them 30
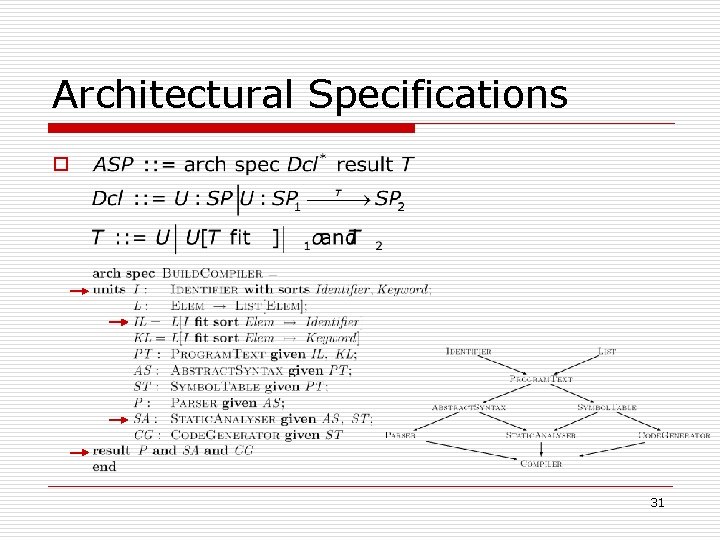
Architectural Specifications o 31

Architectural Specifications Keywords o given: imported units o with: renaming (mapping of symbols) o o o hide/reveal: unit reduction (hide some symbols in unit) and: amalgamation of units fit: fitting an argument to the corresponding formal argument for the generic unit, via a signature morphism in the same 32

Specification Refinement o Fixes some expected properties but says nothing about implementation o Model class becomes smaller and smaller o Techniques: n n Views: model class inclusion Refinement R 1 = SP 1 refined to SP 2 Refinement R 1 = SP 1 refined to arch spec ASP Reducing to implementation of smaller specifications via an architectural specification 33

Tools o o o Hets: The Heterogeneous Tool Set Support for all layers of CASL + CASL sublanguages and extensions Parsing, analysis, proof Supporting multiple logics Hets web-based interface: http: //www. informatik. uni-bremen. de/cgibin/cgiwrap/maeder/hets. cgi Other tools: CASL consistency checker, CASLto. PVS, CATS, HOL-CASL 34
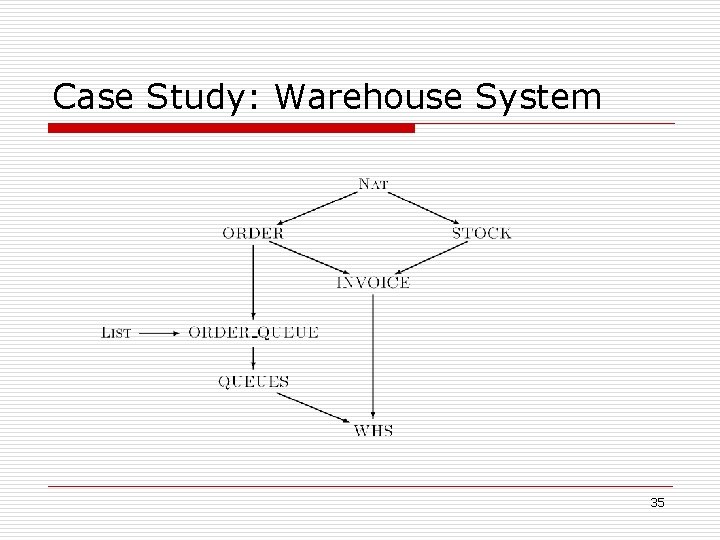
Case Study: Warehouse System 35

Case Study: Warehouse System 36
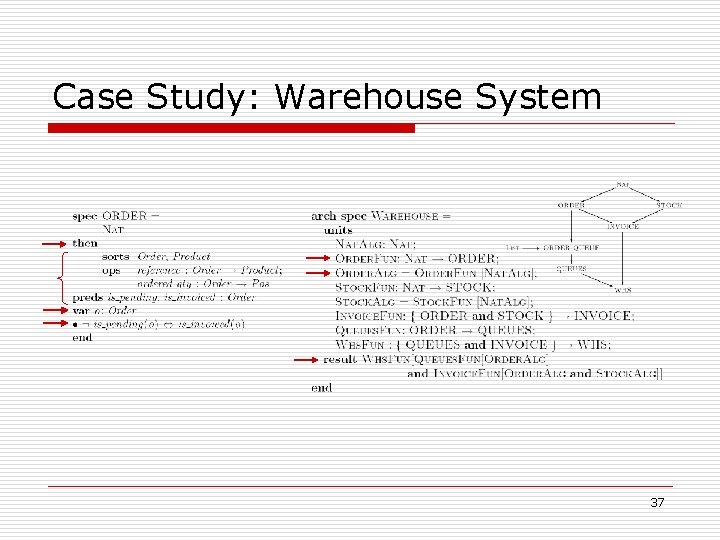
Case Study: Warehouse System 37

Conclusion o o o CASL is a complex specification language that provides formal semantics and proof calculus for all its constructs Orthogonal layers Basic specs: writing theories in a specific logic Structured and architectural specs: logic independent semantics Tool support 38

References o o o T. Mossakowski, A. Haxthausen, D. Sannella and A. Tarlecki. CASL -- the Common Algebraic Specification Language: semantics and proof theory. Computing and Informatics 22: 285 -321 (2003). An extended version of this paper appeared in the book Logics of Specification Languages, 241 --298, D. Bjørner and M. Henson eds. , Springer (2008). P. D. Mosses and M. Bidoit. Casl – The Common Algebraic Specification Language: User Manual, volume 2900 of Lecture Notes in Computer Science, Springer, 2004. P. D. Mosses (ed. ). Casl – The Common Algebraic Specification Language: Reference Manual, volume 2960 of Lecture Notes in Computer Science, Springer, 2004. Hets is available from http: //www. informatik. unibremen. de/agbkb/forschung/formal_methods/Co. FI/hets/. R. Khedri, Formal Methods for Software Specification and Development, Mc. Master University. 39
- Slides: 39