Cascade control of unstable systems with application to

Cascade control of unstable systems with application to stabilization of slug flow Espen Storkaas and Sigurd Skogestad Dep. of Chemical Engineering Norwegian University of Science and Technology Presented at Ad. Chem’ 03 Hong Kong 1

Outline • Unstable systems • Properties of stabilizing control loop • Effect of stabilized poles on higher level control loops • Application to Anti Slug Control 2

Unstable systems • G(s)=C(s. I-A)-1 B+D, unstable if |λi(A)|>0 for any i • Feedback stabilization of G(s) requires active use of inputs – Lower bandwidth limit – Lower limit on H 2 - and H∞-norms of KS = K(I+GK)-1 • Unstable (RHP) zeros and time delay imposes upper limit on bandwidth – Incompatible bandwidth requirements => stabilizing control impossible 3

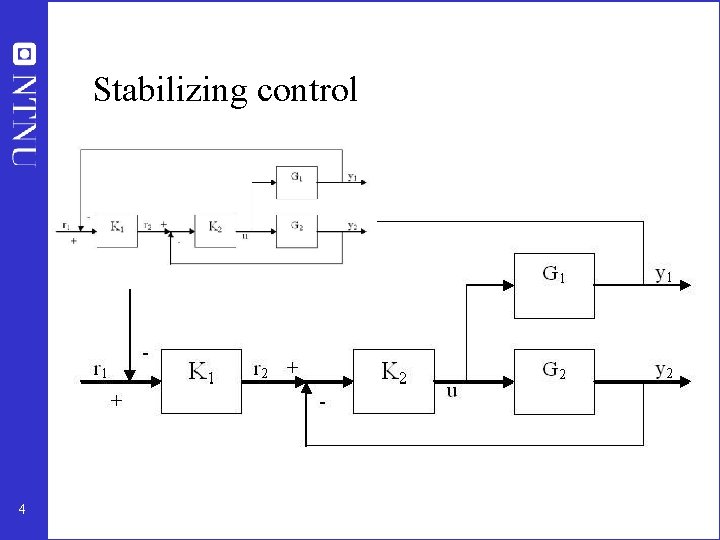
Stabilizing control • • 4 G 2 unstable with RHP poles pi stabilized by K 2 Internal stability S 2=(1+G 2 K 2)-1 contains unstable poles of G 2 as zeros Process as seen from primary layer: G=G 1 S 2 K 2

Effect of stabilizing control on primary control layer Case 1: Unstable poles of G 2 detectable in y 1 – Same unstable poles in G 1 and G 2 • No effect of unstable poles in G 2 on primary control layer – Zeros in S 2 in G=G 1 S 2 K 2 cancelled by poles in G 1 • Bandwidth limitations only from G 1 5

Effect of stabilizing control on primary control layer Case 2 : Unstable poles of G 2 not detectable in y 1 • Unstable poles in G 2 affects the primary loop as RHP zeros in G=G 1 S 2 K 2 • Bandwidth limitation due to unstable G 2: ωB 1<min(pi 2) • May be benificial to operate at faster instabilities 6

Example – Anti Slug Control Experiments performed by the Multiphase Laboratory, NTNU 7

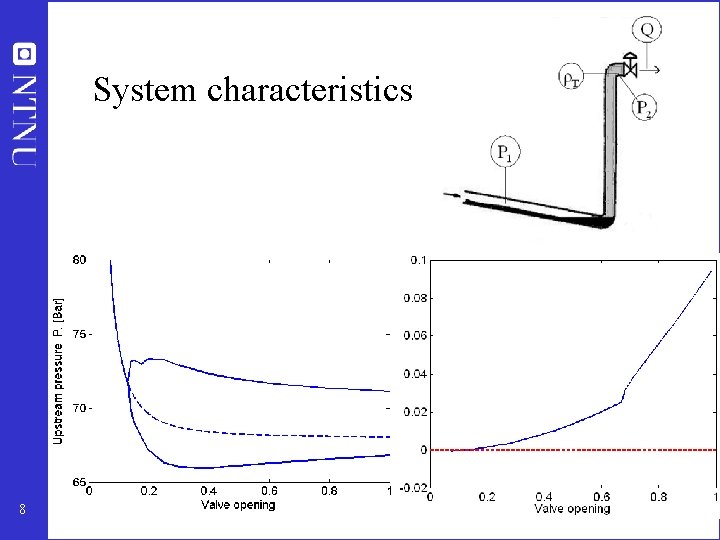
System characteristics 8

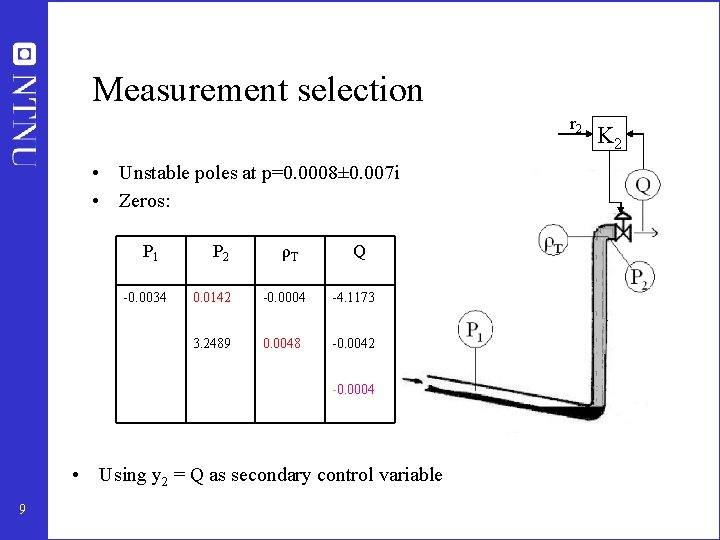
Measurement selection r 2 • Unstable poles at p=0. 0008± 0. 007 i • Zeros: P 1 -0. 0034 P 2 ρT Q 0. 0142 -0. 0004 -4. 1173 3. 2489 0. 0048 -0. 0042 -0. 0004 • Using y 2 = Q as secondary control variable 9 K 2

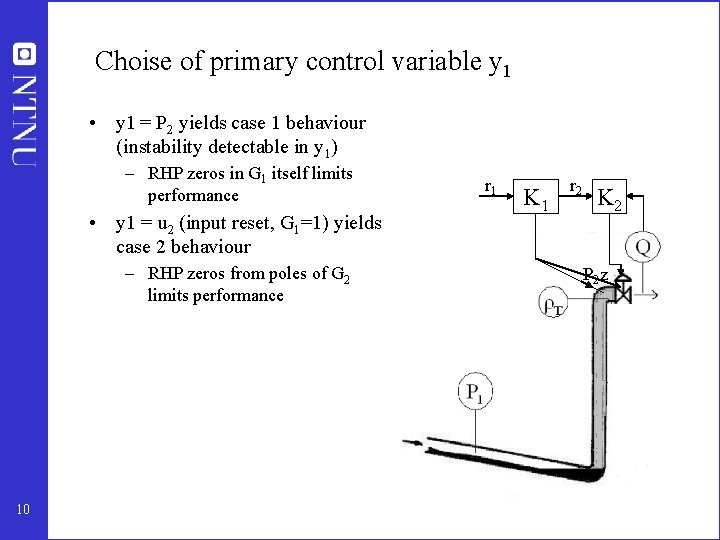
Choise of primary control variable y 1 • y 1 = P 2 yields case 1 behaviour (instability detectable in y 1) – RHP zeros in G 1 itself limits performance • y 1 = u 2 (input reset, G 1=1) yields case 2 behaviour – RHP zeros from poles of G 2 limits performance 10 r 1 K 1 r 2 K 2 P 2 z

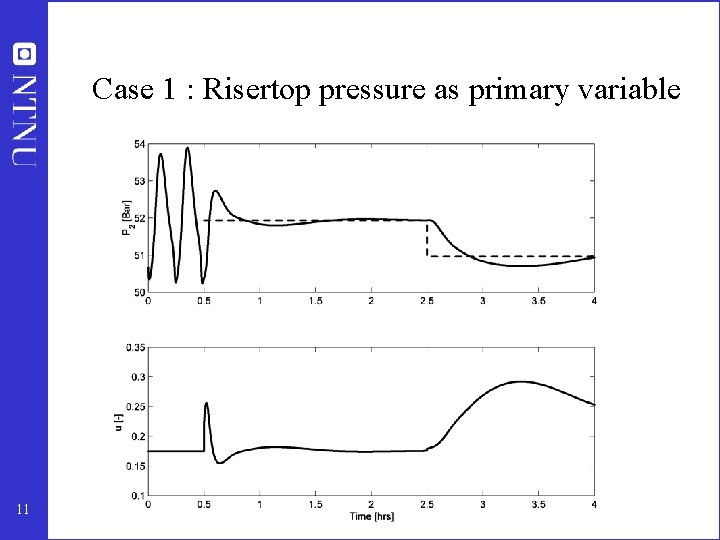
Case 1 : Risertop pressure as primary variable 11

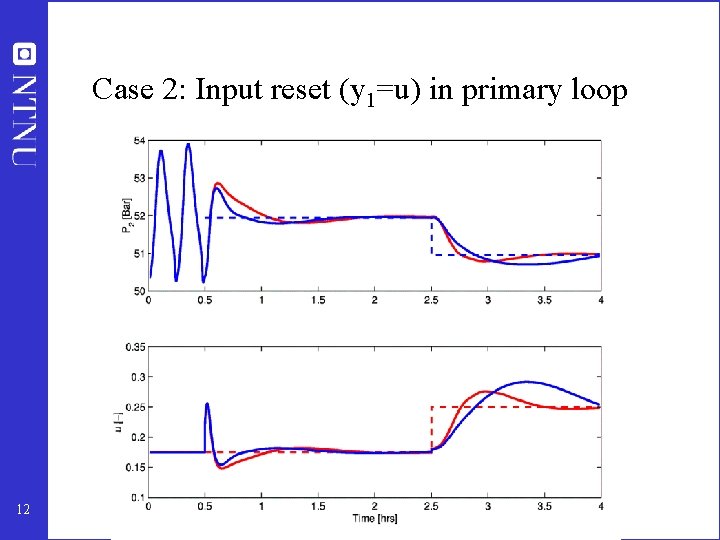
Case 2: Input reset (y 1=u) in primary loop 12

Conclusions • Stabilizied poles will affect the higher level control loops as unstable zeros when unstable poles are not detectable in primary control variables • May be beneficial to operate at faster instabilities if fast responses are needed for the primary control objective • Problem illustrated with stabilization of severe slugging 13

Acknowledgements • Norwegian Research Council for finacial support • ABB and Statoil for supervision and collaboration 14