CAS LX 502 9 a Formal semantics Functions

![S N VP [S N VP]M = true iff [N]M [VP]M, otherwise false S S N VP [S N VP]M = true iff [N]M [VP]M, otherwise false S](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-2.jpg)






![Generalizing our semantics S • M=<U, F> • [Bond]M = F(Bond) = Bond N Generalizing our semantics S • M=<U, F> • [Bond]M = F(Bond) = Bond N](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-9.jpg)
![Generalizing our semantics S • Pass-Up: [b a]M = [a]M N VP • What Generalizing our semantics S • Pass-Up: [b a]M = [a]M N VP • What](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-10.jpg)
![Generalizing our semantics • Functional application: [g a b ]M = [b]M ( [a]M Generalizing our semantics • Functional application: [g a b ]M = [b]M ( [a]M](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-12.jpg)


![argument [ return value ] • x [ x is boring in M argument [ return value ] • x [ x is boring in M](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-16.jpg)
![argument [ return value ] • Change-machine($n-bill) = 4 n quarters. • Change-machine argument [ return value ] • Change-machine($n-bill) = 4 n quarters. • Change-machine](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-17.jpg)
![value argument [ return value ] • Square = n [ n n ] value argument [ return value ] • Square = n [ n n ]](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-18.jpg)
![value argument [ return value ] • Strictly speaking, there’s an intermediate step, which value argument [ return value ] • Strictly speaking, there’s an intermediate step, which](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-19.jpg)
![value argument [ return value ] • One last piece of terminology: Instances of value argument [ return value ] • One last piece of terminology: Instances of](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-20.jpg)

![Like, totally. • What we want [VP]M to be is a function that is Like, totally. • What we want [VP]M to be is a function that is](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-22.jpg)
![Like, totally. • If [Vt] is of type <e, t>>, it is a function Like, totally. • If [Vt] is of type <e, t>>, it is a function](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-23.jpg)

![Like, totally. • [like]M = y [ x [ x likes y in M Like, totally. • [like]M = y [ x [ x likes y in M](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-25.jpg)
![Like, totally. • [like]M = y [ x [ x likes y in M Like, totally. • [like]M = y [ x [ x likes y in M](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-26.jpg)
![x [ x likes Loren in M ] Like, totally. • [VP]M = x [ x likes Loren in M ] Like, totally. • [VP]M =](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-27.jpg)



![and • [and]M = y [ x [ x y ] ] S • and • [and]M = y [ x [ x y ] ] S •](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-32.jpg)


- Slides: 34

CAS LX 502 9 a. Formal semantics Functions and lambda notation
![S N VP S N VPM true iff NM VPM otherwise false S S N VP [S N VP]M = true iff [N]M [VP]M, otherwise false S](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-2.jpg)
S N VP [S N VP]M = true iff [N]M [VP]M, otherwise false S S Conj S S Neg S VP Vt N VP Vi N Pavarotti, … Vi is boring, … Vt likes Conj and, … [S S 1 Conj S 2]M = [Conj]M ( < [S 1]M, [S 2]M > ) [S Neg S´]M = [Neg]M ( [S´]M ). [VP Vt N]M = {x : < x, [N]M > [Vt]M } [Pavarotti]M = F(Pavarotti) [is boring]M = {x: x is boring in M} [likes]M = { <x, y> : x likes y in M } [and]M = {<<true, true>, <true, false>, …} Neg it is not the [iintct]M = {<true, false>, <false, true>} case that

Semantic type • The entire semantics that we are creating here depends on two types of things, individuals and truth values. • We can label individuals as being of type “e” (traditional, think “entity”), and truth values as being of type “t”. • In these terms, names like Bond are of type <e>, and sentences like Bond is hungry are of type <t>.

A formal system of semantic types • <e> is a basic type. • <t> is a basic type. • If a and b are types, <a, b> is a type. • <a, b> is a function that takes something of type a and returns something of type b. • <e, t> is a type. <<e, t>, <e, t>>> is a type. • <e, t, e> is not, nor is <<e, t>>.

Functions • A function transforms one thing into another. • We can define the squaring function as a function that takes a number and gives back that number multiplied with itself • Square(n) = n n • This is a function from numbers to numbers. It takes a number, it gives back a number.

Functions • A function doesn’t need to give back the same kind of thing it gets. Usually, the thing it gives back depends on the thing it gets, but it doesn’t need to be of the same type. • Change-machine($n-bill) = 4 n quarters. • This is a function from bills to quarters.

<e, t> functions • An intransitive verb like is boring can be viewed as a function from individuals to truth values. Given an individual x, it will return true if x is boring, or false if x is not boring. • Boring(x) = true if x is boring; false otherwise. • This is a function from individuals (type <e>) to truth values (type <t>). That is, it has type <e, t>.

Generalizing our semantics • By using this idea that the semantic value of a node in our sentence structure can be a function, we can greatly simplify our semantic rules, basically down to two general rules, and then the lexical rules that tell us specifically what things like is hungry or Bond mean. S N Bond VP Vi is hungry
![Generalizing our semantics S MU F BondM FBond Bond N Generalizing our semantics S • M=<U, F> • [Bond]M = F(Bond) = Bond N](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-9.jpg)
Generalizing our semantics S • M=<U, F> • [Bond]M = F(Bond) = Bond N VP • Type: <e> • [is hungry]M = F(is hungry) = the function f such that, given an individual x, it returns true if x is hungry in M, false otherwise. Bond Vi is hungry • Type: <e, t> The function f such that, given an individual x, it returns true if x is hungry in M, false otherwise
![Generalizing our semantics S PassUp b aM aM N VP What Generalizing our semantics S • Pass-Up: [b a]M = [a]M N VP • What](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-10.jpg)
Generalizing our semantics S • Pass-Up: [b a]M = [a]M N VP • What this says is that if a node b contains nothing else but a node a, then the semantic value of b is going to be exactly the same as the semantic value of a. • So [N]M = [Bond]M = Bond. • [VP]M = [Vi]M = [is hungry]M. Bond Vi is hungry The function f such that, given an individual x, it returns true if x is hungry in M, false otherwise

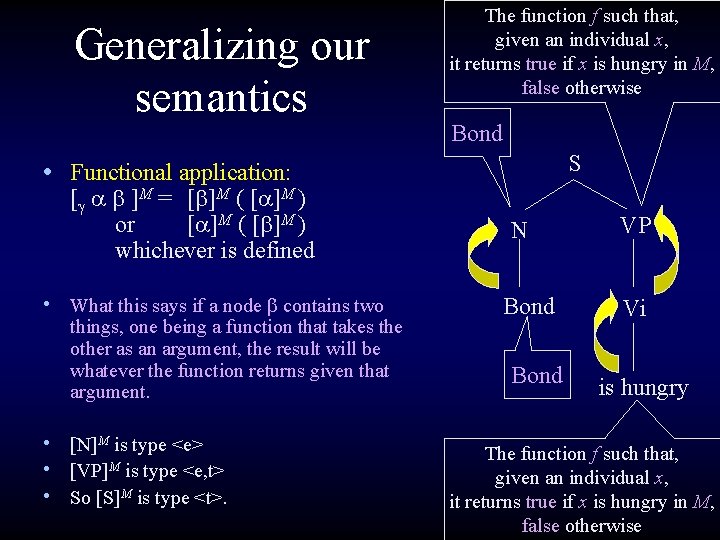
Generalizing our semantics The function f such that, given an individual x, it returns true if x is hungry in M, false otherwise Bond S • Functional application: [g a b ]M = [b]M ( [a]M ) or [a]M ( [b]M ) whichever is defined • What this says if a node b contains two things, one being a function that takes the other as an argument, the result will be whatever the function returns given that argument. • [N]M is type <e> • [VP]M is type <e, t> • So [S]M is type <t>. N Bond VP Vi is hungry The function f such that, given an individual x, it returns true if x is hungry in M, false otherwise
![Generalizing our semantics Functional application g a b M bM aM Generalizing our semantics • Functional application: [g a b ]M = [b]M ( [a]M](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-12.jpg)
Generalizing our semantics • Functional application: [g a b ]M = [b]M ( [a]M ) or [a]M ( [b]M ) whichever is defined • [S]M = [S N VP]M = [VP]M ( [N]M ) • [VP]M is the function such that given an individual x, it returns true if x is hungry in M, false otherwise. • [N]M is the individual Bond. The function f such that, given an individual x, it returns true if x is hungry in M, false otherwise Bond S N Bond VP Vi is hungry The function f such that, given an individual x, it returns true if x is hungry in M, false otherwise

Generalizing our semantics The function f such that, given an individual x, it returns true if x is hungry in M, false otherwise Bond S • Functional application: [g a b ]M = [b]M ( [a]M ) or [a]M ( [b]M ) whichever is defined • [S]M = [S N VP]M = [VP]M ( [N]M ) • So, [S]M is true if Bond is hungry in M, false otherwise. N Bond VP Vi is hungry The function f such that, given an individual x, it returns true if x is hungry in M, false otherwise

Writing functions • So, if we think of everything in terms of functions and arguments, then these two rules, Functional application and Pass-up, will be the only semantic rules we need. • So far, our notation for writing functions is clunky. • [is boring]M = that function f such that, given an individual x, f returns true if x is boring in M, and false otherwise. • It would be nice if we could write that function directly somehow.

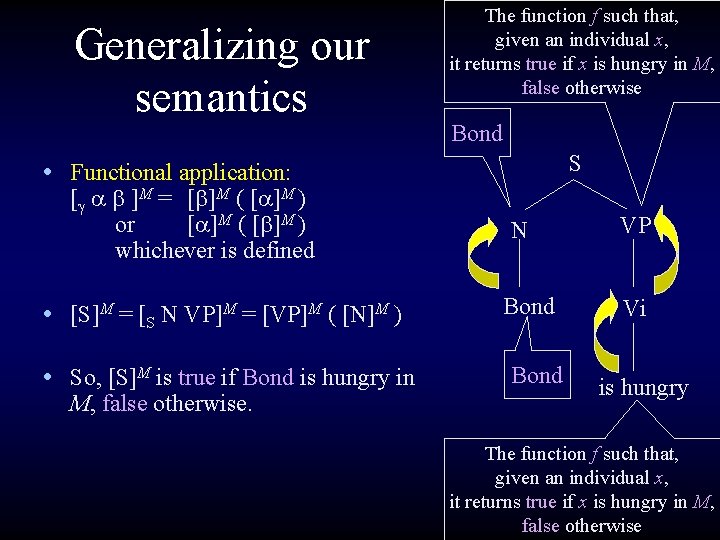
Enter the • Happily, there is a way to write functions like this directly, using lambda notation. • The structure of a function written in lambda notation is: argument [ return value ] • So, for [is boring]M, we can write this: • x [ x is boring in M ] • This is the function such that, given an individual x, returns true if x is boring in M and false otherwise.
![argument return value x x is boring in M argument [ return value ] • x [ x is boring in M](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-16.jpg)
argument [ return value ] • x [ x is boring in M ] • The idea here is that x is boring in M is either true (if x is boring in M) or false (if x is not boring in M), and so whatever truth value x is boring in M has will be what this function returns. • This is a function of type <e, t>.
![argument return value Changemachinenbill 4 n quarters Changemachine argument [ return value ] • Change-machine($n-bill) = 4 n quarters. • Change-machine](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-17.jpg)
argument [ return value ] • Change-machine($n-bill) = 4 n quarters. • Change-machine = $n-bill [ 4 n quarters ] • Square = n [ n n ] • Not very complicated, just a short way to write “that function f such that, given argument, returns return value. ”
![value argument return value Square n n n value argument [ return value ] • Square = n [ n n ]](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-18.jpg)
value argument [ return value ] • Square = n [ n n ] • Square(3) = 3 3 = 9 • Square(4) = 4 4 = 16. • To evaluate a function, we take the value and substitute it in for the argument within the return value. If we give it a 3, and the argument is n, then we replace all of the ns with 3 s and evaluate the return value.
![value argument return value Strictly speaking theres an intermediate step which value argument [ return value ] • Strictly speaking, there’s an intermediate step, which](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-19.jpg)
value argument [ return value ] • Strictly speaking, there’s an intermediate step, which is written like so: • Square = n [ n n ] • Square(3) = 3 n [ n n ] = 3 3 = 9 • Square(4) = 4 n [ n n ] = 4 4 = 16. • What value argument [ return value ] means is: Replace every instance of argument within return value with value, then evaluate return value. • This operation goes by the name lambda conversion.
![value argument return value One last piece of terminology Instances of value argument [ return value ] • One last piece of terminology: Instances of](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-20.jpg)
value argument [ return value ] • One last piece of terminology: Instances of argument within return value are said to be variables that bound by the lambda operator. • Triple = n [ 3 n ] Lambda operator Bound variable

Like, totally. • Transitive verbs, such as like, are • • ultimately relations between S individuals. Yet, our syntax produces structures VP N like this, where VP has only likes and Loren in it. Vt N We know that [S]M needs to be a truth Bond value, it needs to be of type <t>. We know that [N]M is an individual likes Loren (Bond), type <e>. Given the way Functional Application works, [VP]M needs to be a function of type <e, t>.
![Like totally What we want VPM to be is a function that is Like, totally. • What we want [VP]M to be is a function that is](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-22.jpg)
Like, totally. • What we want [VP]M to be is a function that is true of all Loren-likers, such that the whole sentence will be true if Bond is a Loren-liker. S N • So, what is [VP]M? Well, that too has Vt two parts. We know that it needs to be of type <e, t>. We know that one component Bond (N) is an individual of type <e>. So we likes need [Vt] to be something that takes an individual, type <e>, and returns a predicate, type <e, t>. • That is, [Vt] must be type <e, t>>. VP N Loren
![Like totally If Vt is of type e t it is a function Like, totally. • If [Vt] is of type <e, t>>, it is a function](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-23.jpg)
Like, totally. • If [Vt] is of type <e, t>>, it is a function that takes an individual and returns a function, specifically a function from individuals to truth values. S VP N • The particular function we need it to return is the one that is true of Lorenlikers. • So, how do we write that? • Well, argument [ return value ] Bond Vt N likes Loren

Like, totally. • What we’re aiming for is something that will work out to: S • x [ x is a Loren-liker in M ] • But we want to derive x is a Loren-liker in M from like and Loren. (That is, from [Vt]M and [N]M). We know what [N]M is, Bond it’s Loren. So, what’s [Vt]M ? • [like]M = y [ x [ x likes y in M ] ] VP N Vt N likes Loren
![Like totally likeM y x x likes y in M Like, totally. • [like]M = y [ x [ x likes y in M](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-25.jpg)
Like, totally. • [like]M = y [ x [ x likes y in M ] ] Bond S • That is, [like]M is the function that, given an individual y, returns the function that, given an individual x, is true if x likes y in M. • So, what is [VP]M ? Well, it contains Vt and N, and [Vt]M is a function of type <e, t>> that takes an argument of type <e>. [N]M is of type <e>. So, [VP]M = [Vt]M ( [N]M ). Loren VP N Bond y [ x [ x likes y in M ] ] Vt N likes Loren
![Like totally likeM y x x likes y in M Like, totally. • [like]M = y [ x [ x likes y in M](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-26.jpg)
Like, totally. • [like]M = y [ x [ x likes y in M ] ] Bond S • [VP]M = [Vt]M ( [N]M ) Loren VP N • [VP]M = Loren y [ x [ x likes y in M ] ] Bond • …and lambda conversion gives us… • = x [ x likes Loren in M ] y [ x [ x likes y in M ] ] Vt N likes Loren
![x x likes Loren in M Like totally VPM x [ x likes Loren in M ] Like, totally. • [VP]M =](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-27.jpg)
x [ x likes Loren in M ] Like, totally. • [VP]M = x [ x likes Loren in M ] Bond S • Then, we evaluate [S]M. It has two constituents, one a function of type <e, t>, the other an individual of type <e>. Apply Functional Application. • [S]M = [VP]M ( [N]M Loren Bond ) VP N = Bond x [ x likes Loren in M ] = Bond likes Loren in M y [ x [ x likes y in M ] ] Vt N likes Loren

Formal finishing touches • Strictly speaking, we still fudged a bit when we said that • [like]M = y [ x [ x likes y in M ] ] • Really, what we mean is: • [like]M = y [ x [ <x, y> F(like) ] ] • Since F(like) is the set of pairs <liker, likee> where liker and likee are drawn from U.

Generalized semantics • We now have a relatively simple semantic theory. Each node in the (syntactic) structure has a semantic value. If the node has a sister, one of them is a function and one of them is an argument, and the semantic value of both together is whatever the function yields, given the argument (Functional Application). If a node has no sisters, its parent node just has the same semantic value (Pass-up). • The semantic values of the lexical items reflects this structure. So the semantic value of names will be of type <e>, that of intransitive verbs will be of type <e, t>, that of transitive verbs will be of type <e, t>>.

Remaining loose ends • Functional Application only allows for two daughters, but our conjunction rules yield structures will three. We need to change this so that Functional Application will work. • The simplest approach is just to treat and or as if they are something like transitive predicates. That is, type <t, t>>.

Conj. P S • Instead of S S Conj S, we can do this in two steps: S S Conj. P and Conj. P Conj S • Then, we define [and]M as a function that takes a truth value and returns a truth value: <t, t>> S Conj S and S Conj. P S Conj and S
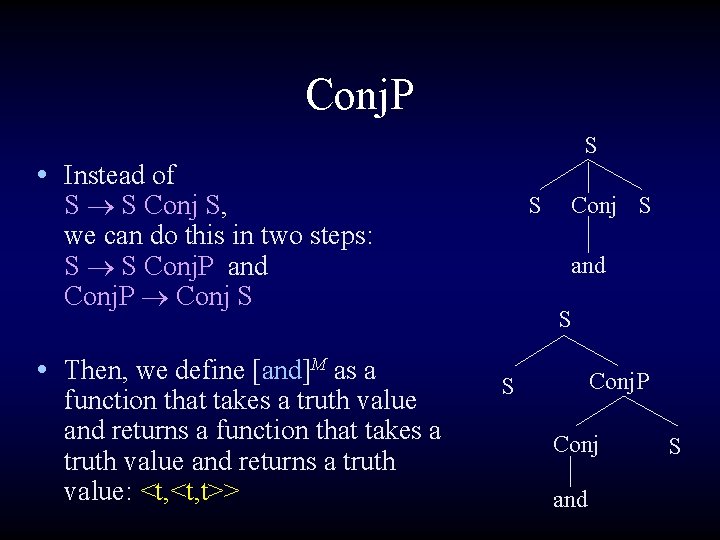
![and andM y x x y S and • [and]M = y [ x [ x y ] ] S •](https://slidetodoc.com/presentation_image/2ce80ccd6bde86fcfa39bb2e59e46298/image-32.jpg)
and • [and]M = y [ x [ x y ] ] S • [Conj. P]M = [Conj]M ( [S 2]M ) = [S 2]M y [ x [ x y ] ] = x [ x [S 2]M ] • [S]M = [Conj. P]M ( [S 1]M ) = [S 1]M x [ x [S 2]M ] = [S 1]M [S 2]M Conj. P S 1 Conj and S 2

S N VP S Neg S S S Conj. P Conj S VP Vt N VP Vi N Pavarotti, … Vi is boring, … Vt likes Conj and, … Neg it is not the case that Pass-Up: [b a]M = [a]M Functional application: [g a b ]M = [b]M ( [a]M ) or [a]M ( [b]M ) whichever is defined [Pavarotti]M = F(Pavarotti) [is boring]M = x [ x F(is boring) ] [likes]M = y [ x [ <x, y> F(likes) ] ] [and]M = y [ x [ x y ] ] [iintct]M = x [ x ]
