Cartesian Schemes Combined with a CutCell Method Evaluated

Cartesian Schemes Combined with a Cut-Cell Method, Evaluated with Richardson Extrapolation D. N. Vedder Prof. Dr. Ir. P. Wesseling Dr. Ir. C. Vuik Prof. W. Shyy

Overview • • • Computational Aero. Acoustics Spatial discretization Time integration Cut-Cell method Testcase • • Richardson extrapolation Interpolation Results Conclusions

Computational Aero. Acoustics • Sound modelled as an inviscid fluid phenomena Euler equations • Acoustic waves are small disturbances Linearized Euler equations:

Computational Aero. Acoustics Dispersion relation • A relation between angular frequency and wavenumber. • Easily determined by Fourier transforms

Spatial discretization OPC • Optimized-Prefactored-Compact scheme 1. Compact scheme xj-2 xj-1 xj xj+1 xj+2 Fourier transforms and Taylor series

Spatial discretization OPC • Taylor series Fourth order gives two equations, this leaves one free parameter.

Spatial discretization OPC • Fourier transforms Theorems:

Spatial discretization OPC

Spatial discretization OPC Optimization over free parameter:

Spatial discretization OPC 2. Prefactored compact scheme Determined by

Spatial discretization OPC 3. Equivalent with compact scheme Advantages: 1. Tridiagonal system two bidiagonal systems (upper and lower triangular) 2. Stencil needs less points

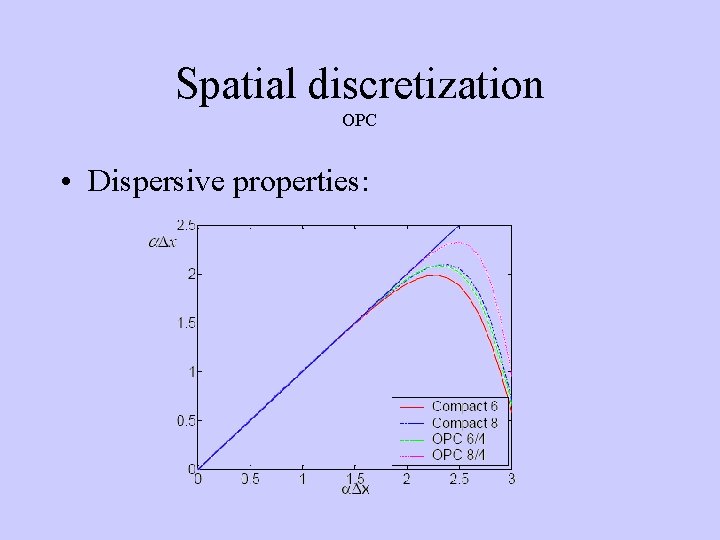
Spatial discretization OPC • Dispersive properties:

Time Integration LDDRK • Low-Dissipation-and-Dispersion Runge. Kutta scheme

Time Integration LDDRK • Taylor series • Fourier transforms • Optimization • Alternating schemes

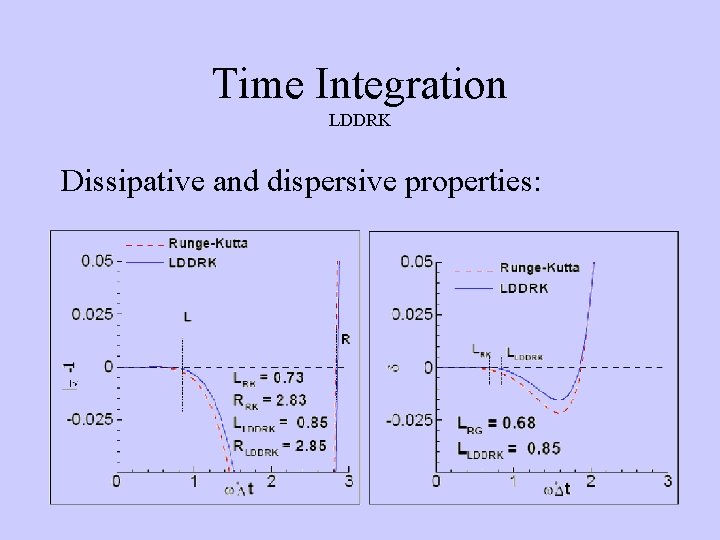
Time Integration LDDRK Dissipative and dispersive properties:

Cut-Cell Method • Cartesian grid • Boundary implementation • Cut-cell method: – Cut cells can be merged – Cut cells can be independent

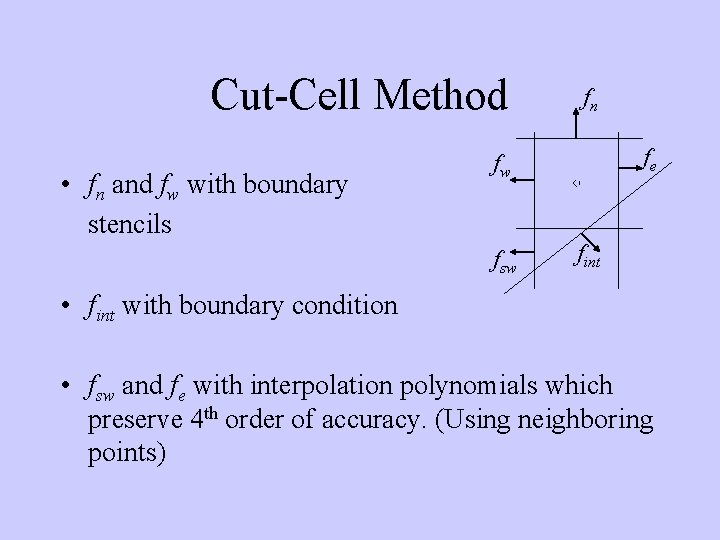
Cut-Cell Method • fn and fw with boundary stencils fn fe fw fsw fint • fint with boundary condition • fsw and fe with interpolation polynomials which preserve 4 th order of accuracy. (Using neighboring points)

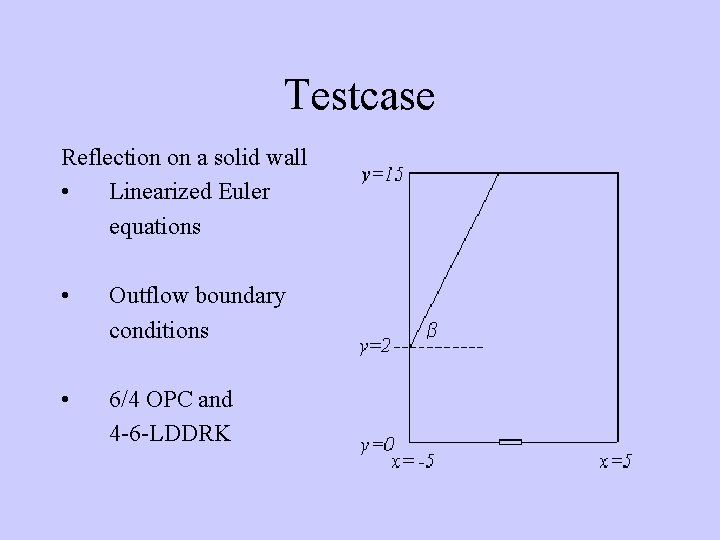
Testcase Reflection on a solid wall • Linearized Euler equations • Outflow boundary conditions • 6/4 OPC and 4 -6 -LDDRK

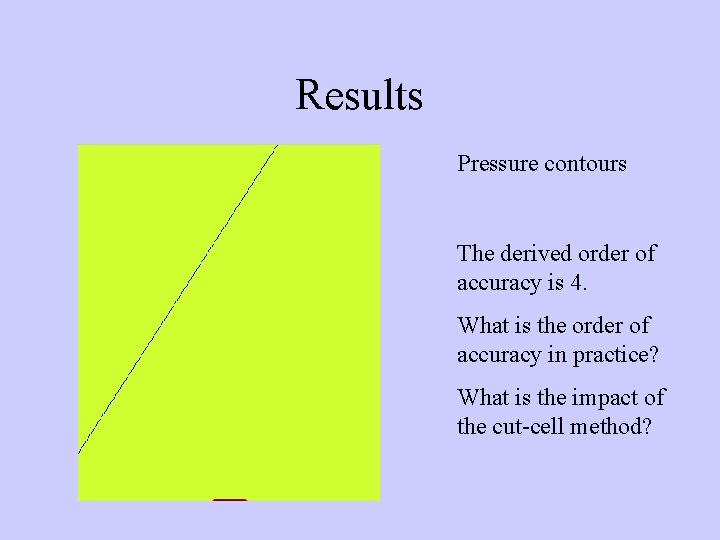
Results Pressure contours The derived order of accuracy is 4. What is the order of accuracy in practice? What is the impact of the cut-cell method?

Richardson extrapolation Determining the order of accuracy Assumption:

Richardson extrapolation Three numerical solutions needed Pointwise approach interpolation to a common grid needed

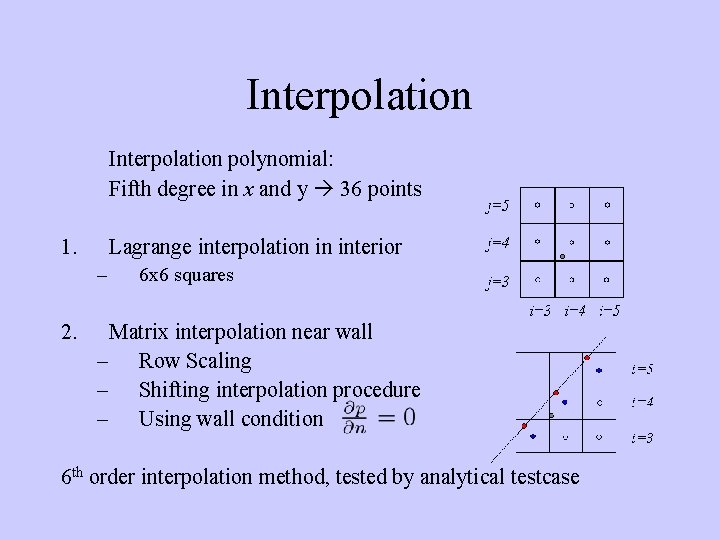
Interpolation polynomial: Fifth degree in x and y 36 points 1. Lagrange interpolation in interior – 2. 6 x 6 squares Matrix interpolation near wall – Row Scaling – Shifting interpolation procedure – Using wall condition 6 th order interpolation method, tested by analytical testcase

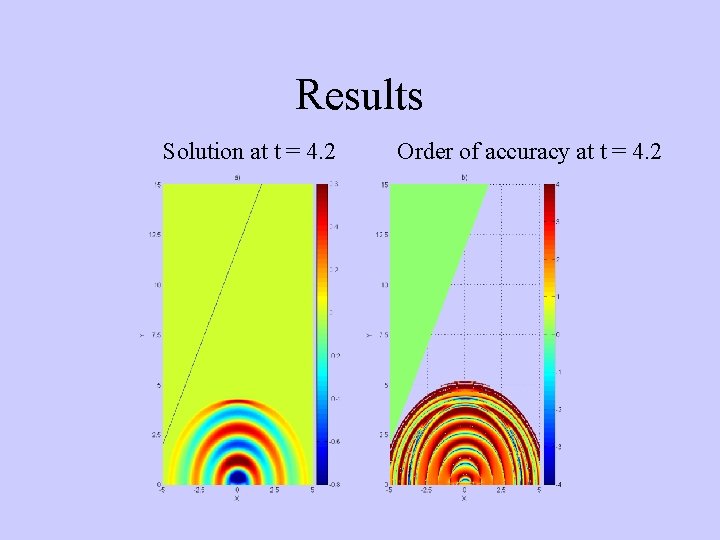
Results Solution at t = 4. 2 Order of accuracy at t = 4. 2

Results (cont) Impact of boundary condition and filter • Boundary condition • Filter for removing high frequency noise

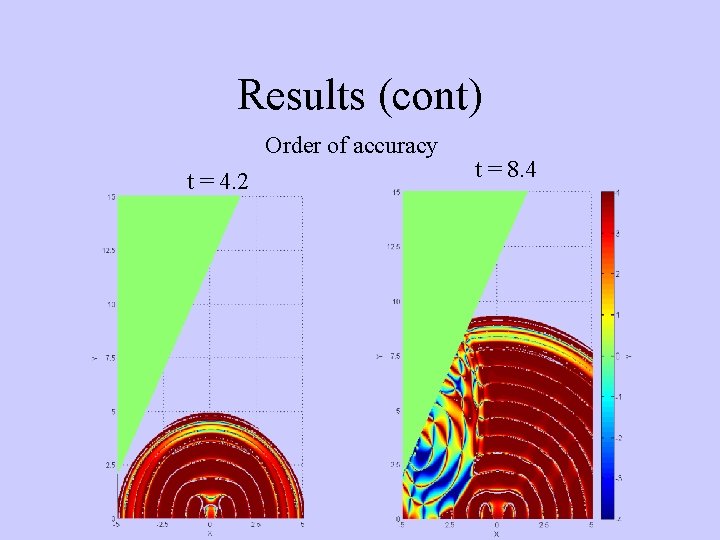
Results (cont) Order of accuracy t = 4. 2 t = 8. 4

Results (cont) Impact of outflow condition • Outflow boundary condition • Replace by solid wall

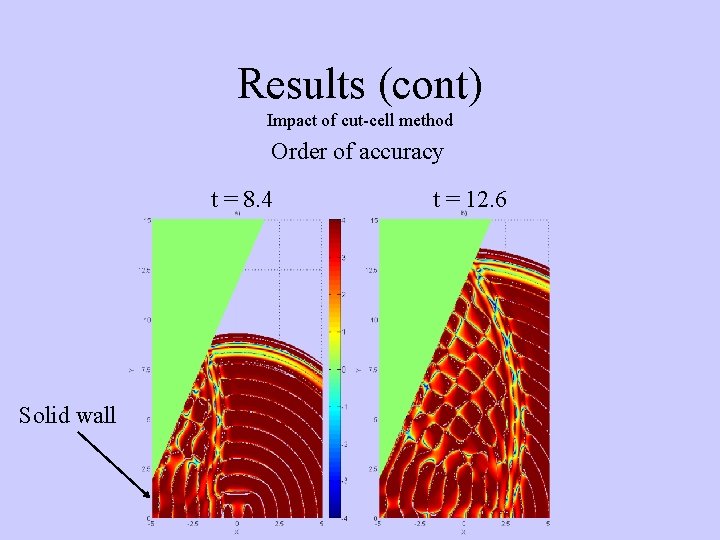
Results (cont) Impact of cut-cell method Order of accuracy t = 8. 4 Solid wall t = 12. 6

Results (cont) fn Impact of cut-cell method • Interpolation method used for fsw and fe fsw • Tested by analytical testcase • Results obtained with three norms – Order of accuracy about 0!! fe fw fint

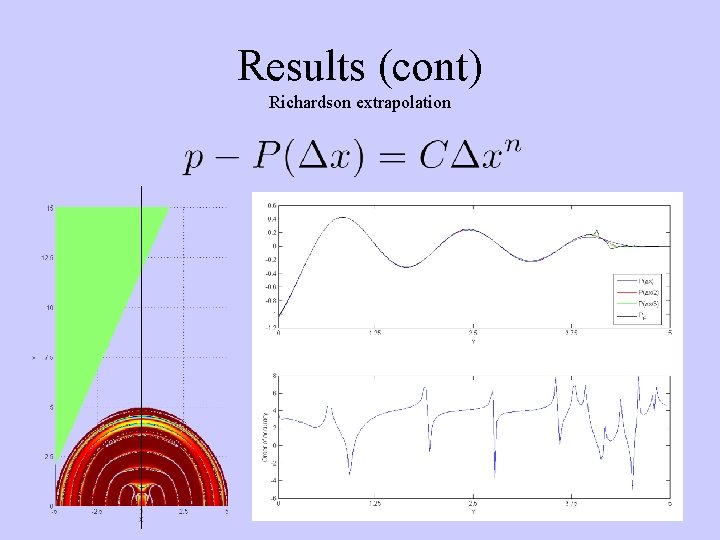
Results (cont) Richardson extrapolation

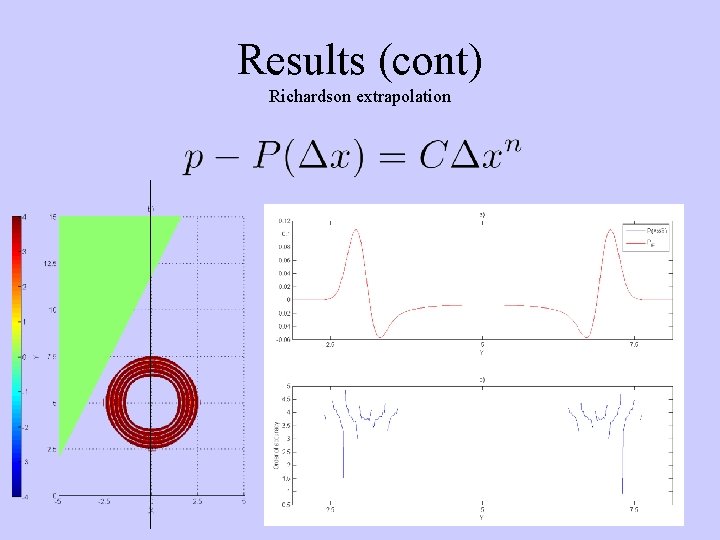
Results (cont) Richardson extrapolation

Conclusions • Interpolation to common grid – 6 th order to preserve accuracy of numerical solution • Impact of discontinuities and filter – Negative impact on order of accuracy • Impact of outflow boundary conditions – Can handle waves from only one direction • Impact of cut-cell method – Lower order of accuracy due to interpolation • Richardson extrapolation – Only for “smooth” problems

Questions?