Carry LookAhead Adders ECE 352 Digital System Fundamentals

Carry Look-Ahead Adders ECE 352 Digital System Fundamentals Carry Look-Ahead Adders 1

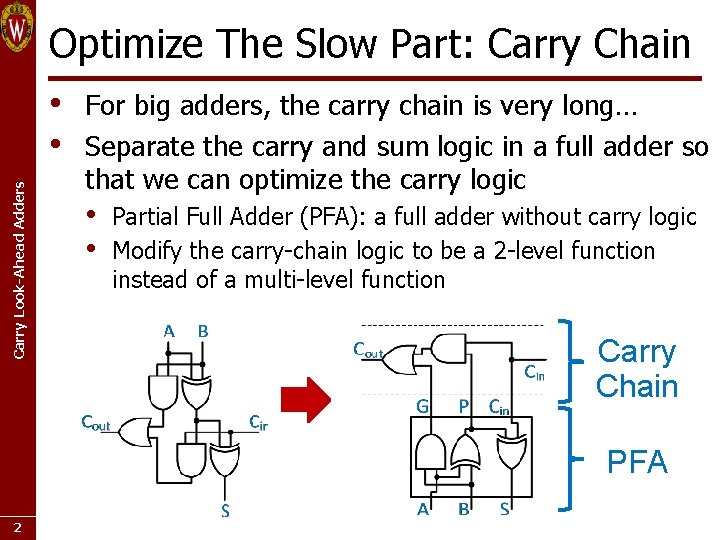
Optimize The Slow Part: Carry Chain Carry Look-Ahead Adders • • For big adders, the carry chain is very long… Separate the carry and sum logic in a full adder so that we can optimize the carry logic • • Partial Full Adder (PFA): a full adder without carry logic Modify the carry-chain logic to be a 2 -level function instead of a multi-level function Carry Chain PFA 2

Carry Look-Ahead Adder (CLA) Carry Look-Ahead Adders • 3 • As usual, can trade area/power for speed • • Multi-level logic (ripple carry) reduces area Flattening carry logic increases speed Make carry logic a 2 -level function of: • • Generate (G) • “Based on the operand values at just this bit position, will the carry-out for this position be 1 regardless of the carry-in? ” Propagate (P) • “Based on the operand values at just this bit position, will the carry-out for this position be equal to the carry-in? ”

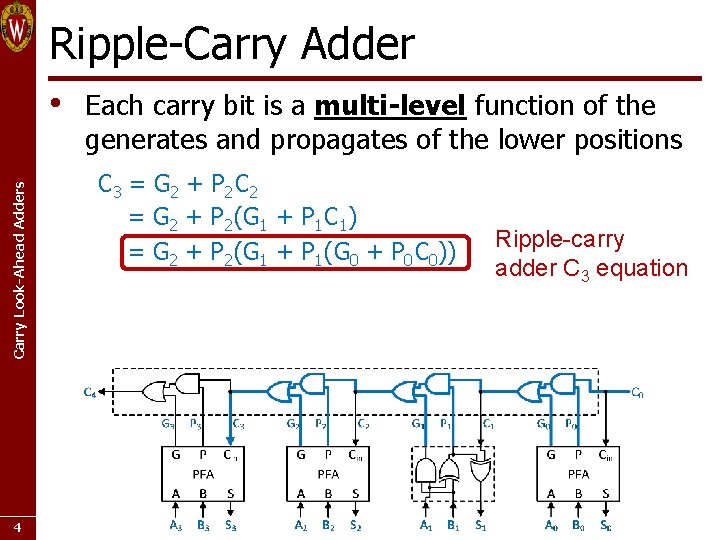
Ripple-Carry Adder Carry Look-Ahead Adders • 4 Each carry bit is a multi-level function of the generates and propagates of the lower positions C 3 = G 2 + P 2 C 2 = G 2 + P 2 (G 1 + P 1 C 1) = G 2 + P 2 (G 1 + P 1 (G 0 + P 0 C 0)) Ripple-carry adder C 3 equation

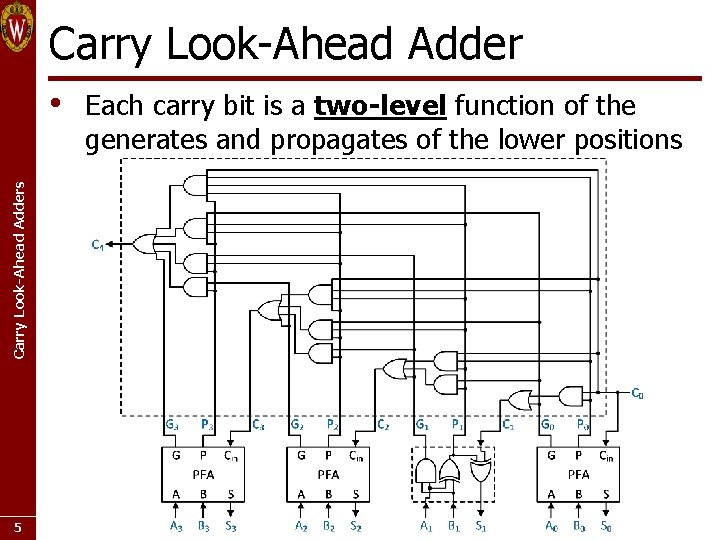
Carry Look-Ahead Adders • 5 Each carry bit is a two-level function of the generates and propagates of the lower positions

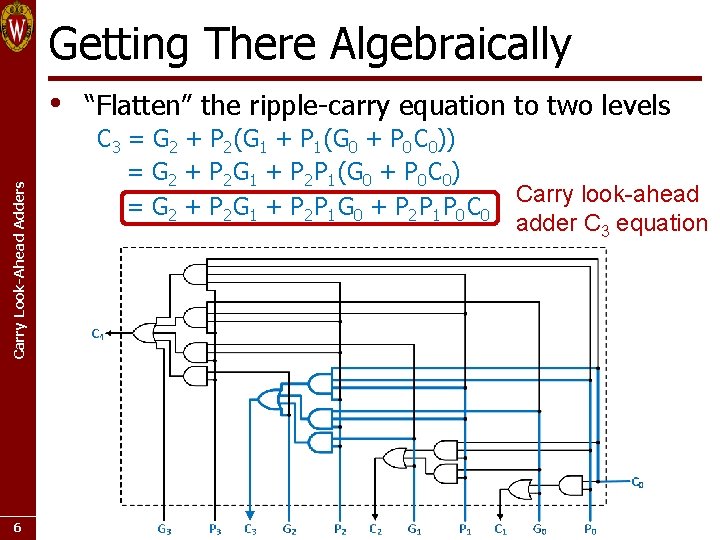
Getting There Algebraically Carry Look-Ahead Adders • 6 “Flatten” the ripple-carry equation to two levels C 3 = G 2 + P 2 (G 1 + P 1 (G 0 + P 0 C 0)) = G 2 + P 2 G 1 + P 2 P 1 (G 0 + P 0 C 0) = G 2 + P 2 G 1 + P 2 P 1 G 0 + P 2 P 1 P 0 Carry look-ahead adder C 3 equation

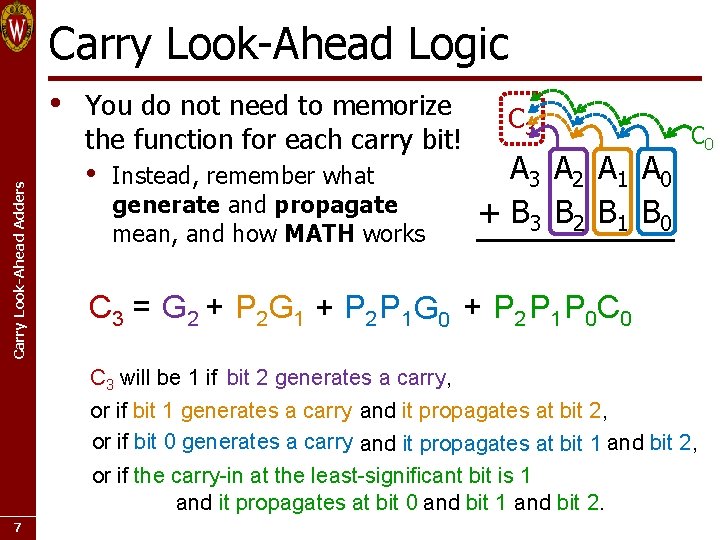
Carry Look-Ahead Logic Carry Look-Ahead Adders • You do not need to memorize the function for each carry bit! • Instead, remember what generate and propagate mean, and how MATH works C 3 A 2 A 1 A 0 + B 3 B 2 B 1 B 0 C 3 = G 2 + P 2 G 1 + P 2 P 1 G 0 + P 2 P 1 P 0 C 3 will be 1 if bit 2 generates a carry, or if bit 1 generates a carry and it propagates at bit 2, or if bit 0 generates a carry and it propagates at bit 1 and bit 2, or if the carry-in at the least-significant bit is 1 and it propagates at bit 0 and bit 1 and bit 2. 7

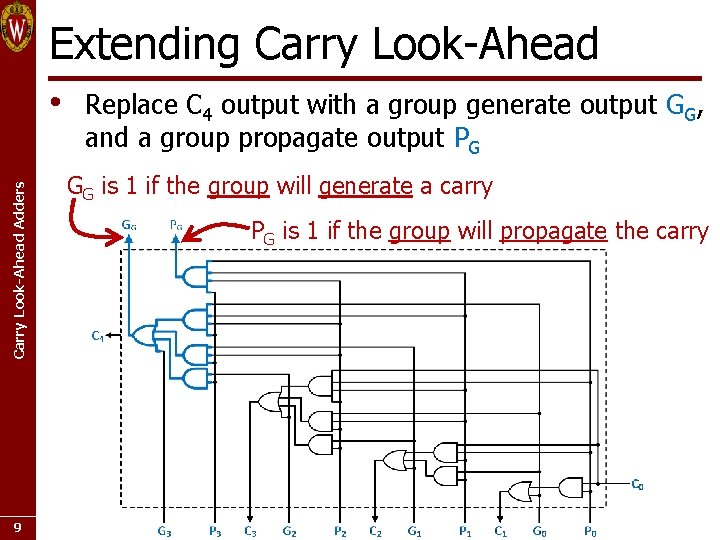
Extending Carry Look-Ahead Adders • • • There is a practical limit on the size of gates… How can we make wider adders? Hierarchy! • • • 8 Higher carry indices require more AND gates and a bigger OR gate Add look-ahead outputs indicating if the 4 -bit group of PFAs generate or propagate a carry to the next group A higher-level look-ahead block uses group generates and propagates to determine carry-ins for each group Same idea as before, but for a group of bits • • “Does this GROUP generate a carry? ” “Does this GROUP propagate a carry? ”

Extending Carry Look-Ahead Adders • 9 Replace C 4 output with a group generate output GG, and a group propagate output PG GG is 1 if the group will generate a carry PG is 1 if the group will propagate the carry

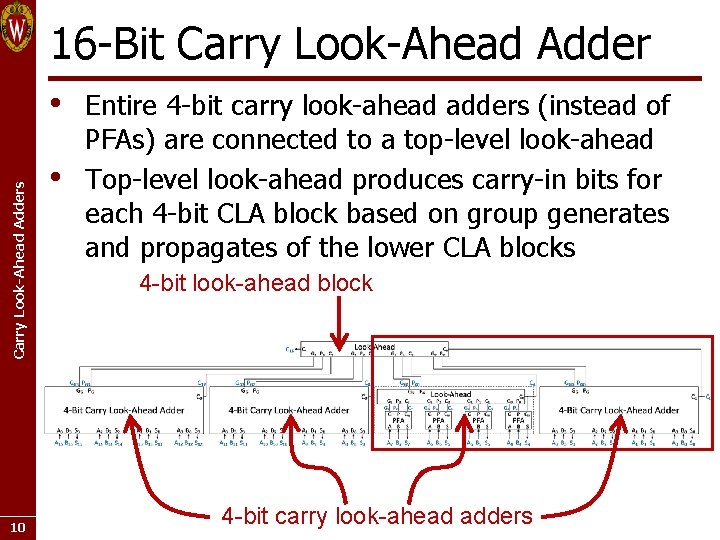
16 -Bit Carry Look-Ahead Adders • 10 • Entire 4 -bit carry look-ahead adders (instead of PFAs) are connected to a top-level look-ahead Top-level look-ahead produces carry-in bits for each 4 -bit CLA block based on group generates and propagates of the lower CLA blocks 4 -bit look-ahead block 4 -bit carry look-ahead adders

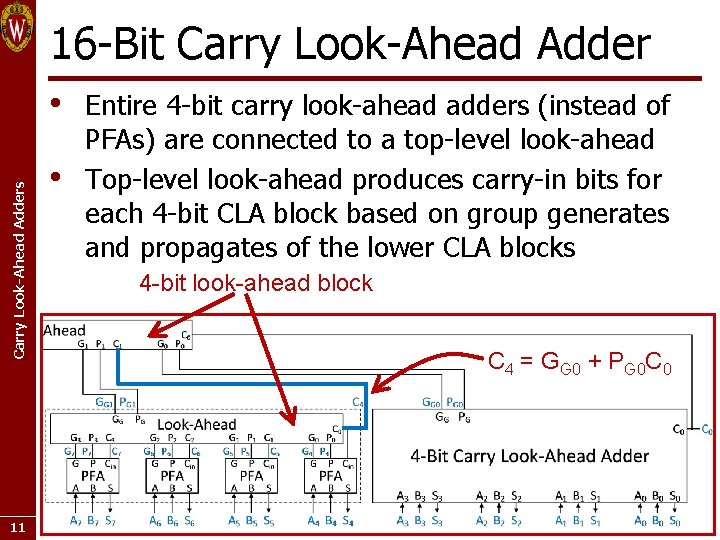
16 -Bit Carry Look-Ahead Adders • 11 • Entire 4 -bit carry look-ahead adders (instead of PFAs) are connected to a top-level look-ahead Top-level look-ahead produces carry-in bits for each 4 -bit CLA block based on group generates and propagates of the lower CLA blocks 4 -bit look-ahead block C 4 = GG 0 + PG 0 C 0

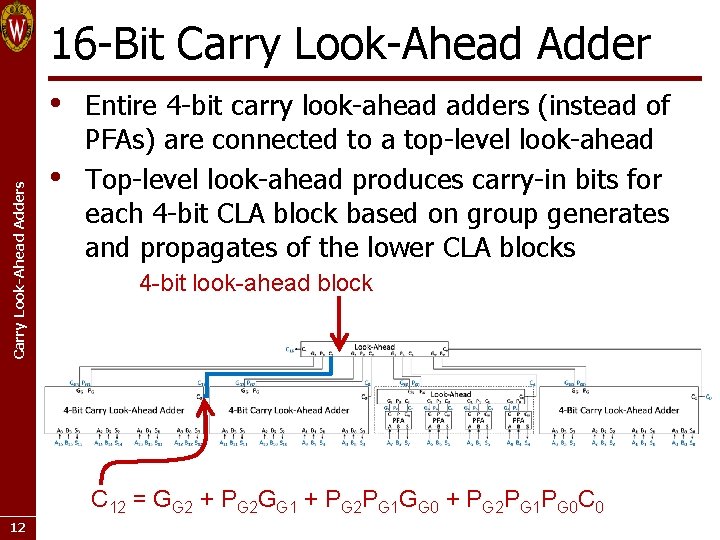
16 -Bit Carry Look-Ahead Adders • • Entire 4 -bit carry look-ahead adders (instead of PFAs) are connected to a top-level look-ahead Top-level look-ahead produces carry-in bits for each 4 -bit CLA block based on group generates and propagates of the lower CLA blocks 4 -bit look-ahead block C 12 = GG 2 + PG 2 GG 1 + PG 2 PG 1 GG 0 + PG 2 PG 1 PG 0 C 0 12

Extending Further… Carry Look-Ahead Adders • • • Each 16 -bit CLA would need a group generate and a group propagate output in its top-level look-ahead • • 13 We can make even larger carry look-ahead adders by adding more levels of hierarchy Build a 64 -bit CLA with four 16 -bit CLAs plus another look-ahead block Does this group of 16 bits generate a carry? Does this group of 16 bits propagate a carry? Hierarchical CLA carry chain is no longer two-level • But far fewer levels than if it were a ripple-carry adder! CLA delay grows more slowly with operand size

Carry Look-Ahead Adders ECE 352 Digital System Fundamentals Carry Look-Ahead Adders 14