Carnegie Mellon Optimized Parallel Distribution Load Flow Solver

Carnegie Mellon Optimized Parallel Distribution Load Flow Solver on Commodity Multi-core CPU Tao Cui (Presenter) Franz Franchetti Dept. of ECE. Carnegie Mellon University Pittsburgh PA tcui@ece. cmu. edu This work is supported by NSF 0931978 & 1116802

Carnegie Mellon Smart Grids Image by Dr. M. Sanchez 2

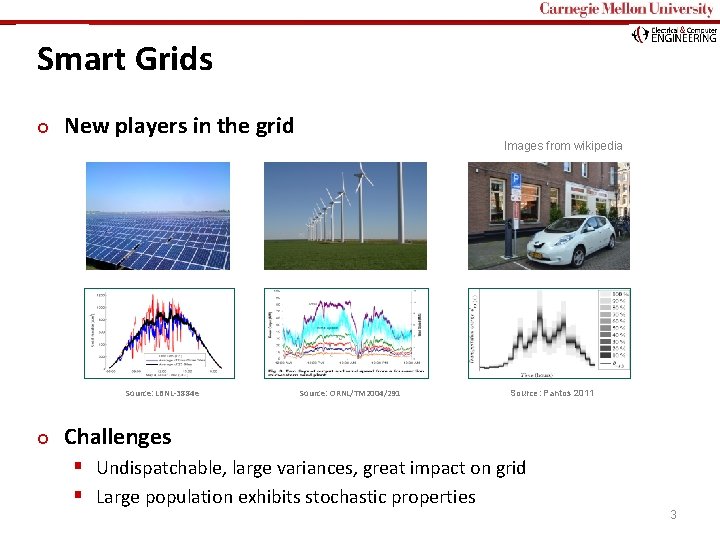
Carnegie Mellon Smart Grids ¢ New players in the grid Source: LBNL-3884 e ¢ Images from wikipedia Source: ORNL/TM 2004/291 Source: Pantos 2011 Challenges § Undispatchable, large variances, great impact on grid § Large population exhibits stochastic properties 3

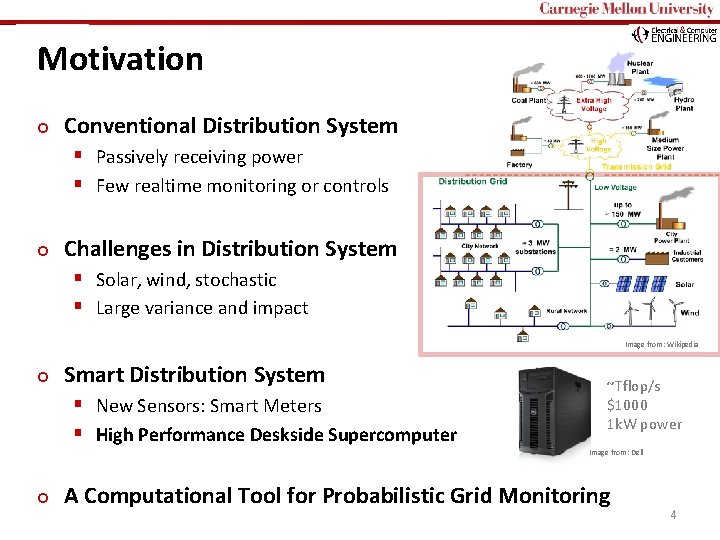
Carnegie Mellon Motivation ¢ Conventional Distribution System § Passively receiving power § Few realtime monitoring or controls ¢ Challenges in Distribution System § Solar, wind, stochastic § Large variance and impact Image from: Wikipedia ¢ Smart Distribution System § New Sensors: Smart Meters § High Performance Deskside Supercomputer ~Tflop/s $1000 1 k. W power Image from: Dell ¢ A Computational Tool for Probabilistic Grid Monitoring 4

Carnegie Mellon Outline ¢ Motivation ¢ Distribution System Load Flow Analysis ¢ Code Optimization ¢ Real Time Implementation ¢ Conclusion 5

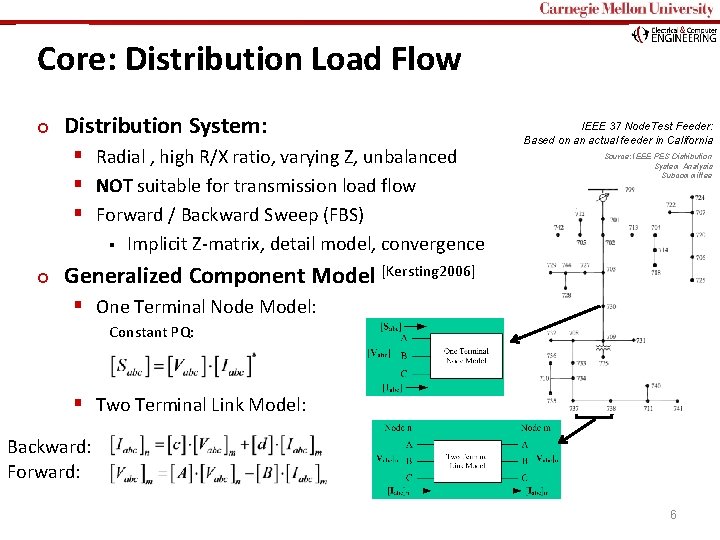
Carnegie Mellon Core: Distribution Load Flow ¢ Distribution System: § Radial , high R/X ratio, varying Z, unbalanced § NOT suitable for transmission load flow § Forward / Backward Sweep (FBS) § ¢ IEEE 37 Node. Test Feeder: Based on an actual feeder in California Source: IEEE PES Distribution System Analysis Subcommittee Implicit Z-matrix, detail model, convergence Generalized Component Model [Kersting 2006] § One Terminal Node Model: Constant PQ: § Two Terminal Link Model: Backward: Forward: 6

Carnegie Mellon Core: Distribution Load Flow ¢ Forward / Backward Sweep [Kersting 2006] Forward Backward IEEE 4 Node Test Feeder Example § Branch current based § Input: substation voltage, load; output: all node voltages § Steps: § § § 1: Initial current = 0, Initial voltage V = V 0; 2: Compute node current In using Node model; 3: Backward: Compute branch current Ib using Link model & KCL; 4: Forward: Update Vk+1 = Vk based on Ib over Link model; 5: Check convergence (|d. S|<Error Limit) stop or go to step 2. 7

Carnegie Mellon Core: Distribution Load Flow ¢ 3 -Phase Voltage on IEEE 37 Nodes Test Feeder Phase A Phase C Phase B 0. 90 ANSI C 84. 1: Nominal: 115, Range A: 110~126 V Range B: 107~127 V Nominal 1. 1 8

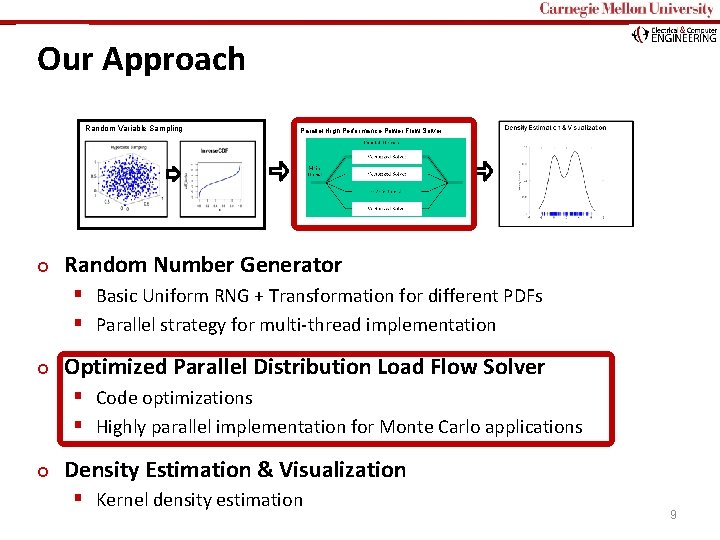
Carnegie Mellon Our Approach Random Variable Sampling ¢ Parallel High Performance Power Flow Solver Random Number Generator § Basic Uniform RNG + Transformation for different PDFs § Parallel strategy for multi-thread implementation ¢ Optimized Parallel Distribution Load Flow Solver § Code optimizations § Highly parallel implementation for Monte Carlo applications ¢ Density Estimation & Visualization § Kernel density estimation 9

Carnegie Mellon Outline ¢ Motivation ¢ Distribution System Load Flow Analysis ¢ Code Optimization ¢ Real Time Implementation ¢ Conclusion 10

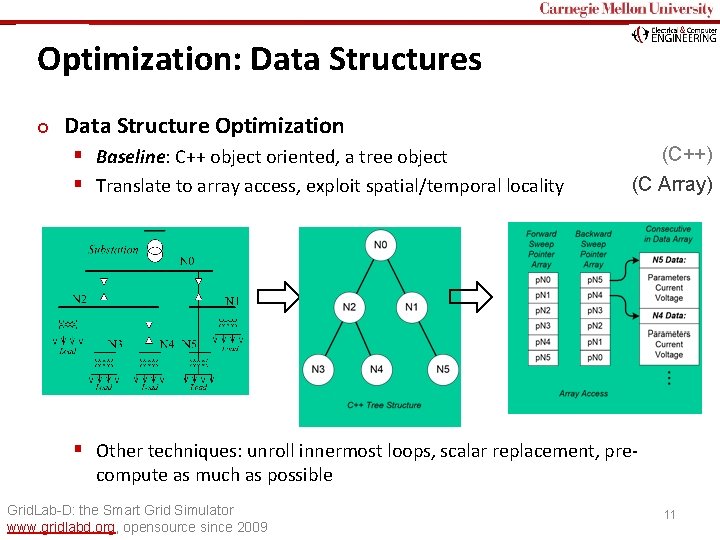
Carnegie Mellon Optimization: Data Structures ¢ Data Structure Optimization § Baseline: C++ object oriented, a tree object § Translate to array access, exploit spatial/temporal locality (C++) (C Array) § Other techniques: unroll innermost loops, scalar replacement, precompute as much as possible Grid. Lab-D: the Smart Grid Simulator www. gridlabd. org, opensource since 2009 11

Carnegie Mellon Optimization: Pattern Based Syntehsis ¢ Algorithm-level Optimization (C Pattern) § Pattern based matrix-vector multiplication For A, B, c, d matrices: § Multi-grounded Cable: diagonal matrix § Ignore shunt & coupling: c = 0, d = I, A = I switch (mat_type){ case real_diag_equal_mat: output[0] = *constant * input[0]; . . . output[5] = *constant * input[5]; break; case imag_diag_equal_mat: output[0] = -*constant * input[3]; output[1] = -*constant * input[4]; output[2] = -*constant * input[5]; output[3] = *constant * input[0]; output[4] = *constant * input[1]; output[5] = *constant * input[2]; break; . . . } … case 1: code 1 case 2: code 2 case N: code N Reduce unnecessary operations Reduce unnecessary storage for better memory access Similar to [Belgin 2009] 12

Carnegie Mellon Data Parallelism (SIMD) ¢ SIMD parallelization xmm 0 § SIMD: Single Instruction Multiple Data vector register xmm 1 vector operation addps xmm 0, xmm 1 SSE: Streaming SIMD Extensions xmm 0 § 128 bit, 4 floats in one register 4 -way SSE example § eg. 4 “fadd” at cost of 1 “addps” AVX: Advanced Vector e. Xtensions (256 bit, 8 floats), Larrabee (512 bit, 16 floats) § Vectorized solver on SIMD level for MCS: (SIMD) § Assumptions & Limitations: converge at same step 13

Carnegie Mellon Variant Synthesis with SPIRAL Symbolic process [Puschel 2005]: § pattern based matrix vector product code … case 1: case 2: case N: SPL Compiler ¢ 14

Carnegie Mellon Multithreading ¢ Multithreading, Run across All CPUs § § Vectorized load flow solver in each thread (Multi-Core) Each thread pinned to a physical core exclusively Fully utilize computation power of Multi-core CPUs Double buffer (automatic load balancing for MCS application) 15

Carnegie Mellon Performance Results: Across Sizes ¢ Performance of Optimized Code, Mass Amount Load Flow Pseudo flop/s: >60 % peak Flop/s: 50% Peak 16

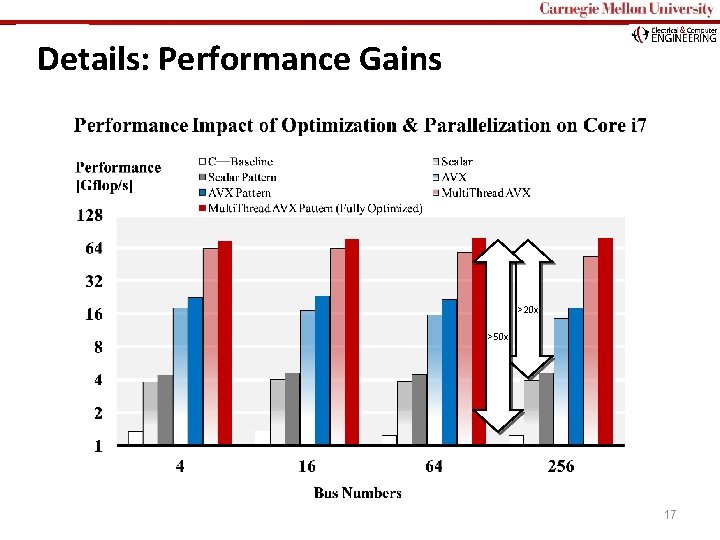
Carnegie Mellon Details: Performance Gains >20 x >50 x 17

Carnegie Mellon Performance Results: Across Machines Problem Size (IEEE Test Feeders) Appro x. flops Approx. Time / Core 2 Extreme Approx. Time / Core i 7 IEEE 37: one iteration 12 K ~ 0. 3 us IEEE 37: one load flow (5 Iter) 60 K ~ 1. 5 us IEEE 37: 1 million load flow 60 G Baseline. C++ ICC –o 3 (~300 x faster then pure Matlab scripts) Comments 0. 01 k. VA error 18 ~<2 s ~<1 s ~ 60 s (>5 hrs Matlab) SCADA Interval:

Carnegie Mellon Accuracy ¢ Convergence of Monte Carlo § Very crude. MCG 59+ICDF, 50 trials with “time(NULL)” seeds ge lta o t: V 738 u O de No on In: Active Power P~ u=0, std=100 kw on Phase A of Node 738, 711, 741 19

Carnegie Mellon Outline ¢ Motivation ¢ Distribution System Load Flow Analysis ¢ Code Optimization ¢ Real Time Implementation ¢ Conclusion 20

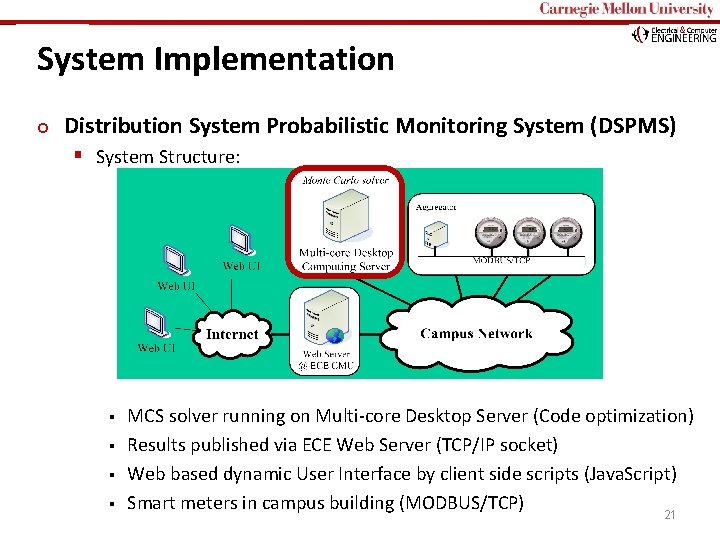
Carnegie Mellon System Implementation ¢ Distribution System Probabilistic Monitoring System (DSPMS) § System Structure: § § MCS solver running on Multi-core Desktop Server (Code optimization) Results published via ECE Web Server (TCP/IP socket) Web based dynamic User Interface by client side scripts (Java. Script) Smart meters in campus building (MODBUS/TCP) 21

Carnegie Mellon System Implementation ¢ Distribution System Probabilistic Monitoring System (DSPMS) § Web Server and User Interface § Link: www. ece. cmu. edu/~tcui/test/Dist. Sim/DSPMS. htm 22

Carnegie Mellon Conclusion ¢ Smart Distribution Network: Impact of renewable and stochastic source: LBNL-3884 e ¢ ¢ Commodity HPC & code optimization: Millions of cases /sec on $1 K class machine Distribution System Probabilistic Monitor: A prove of concept real time application 23

Carnegie Mellon References ¢ ¢ ¢ ¢ [LBNL-3884 E]. Mills, A. Implications of Wide-Area Geographic Diversity for Short-Term Variability of Solar Power, LBNL-3884 E. Lawrence Berkeley National Laboratory, Berkeley, [ORNL/TM 2004/291]. B. Kirby, "Frequency Regulation Basics and Trends, " ORNL/TM 2004/291, Oak Ridge National Laboratory, December 2004. [Pantos 2011]. Miloš Pantoš Stochastic optimal charging of electric-drive vehicles with renewable energy Energy, Volume 36, Issue 11, November 2011 [Ghosh 97]. A. K. Ghosh, D. L. Lubkeman, M. J. Downey, R. H. Jones “Distribution Circuit State Estimation Using a Probabilistic Approach, ” IEEE Transactions on Power Systems, vol. 12, no. 1, pp. 45 -51, 1997 [Belgin 2009]. M. Belgin, G. Back, and C. J. Ribbens, “Pattern-based sparse matrix representation for memory-efficient smvm kernels, ” in Proceedings of the 23 rd international conference on Supercomputing, ser. ICS ’ 09. New York, NY, USA: ACM, 2009, pp. 100– 109. [Puschel 2005]. M. Puschel, J. M. F. Moura, J. Johnson, D. Padua, M. Veloso, B. Singer, J. Xiong, F. Franchetti, A. Gacic, Y. Voronenko, K. Chen, R. W. Johnson, and N. Rizzolo, “SPIRAL: Code generation for DSP transforms, ” Proceedings of the IEEE, special issue on “Program Generation, Optimization, and Adaptation”, vol. 93, no. 2, pp. 232– 275, 2005. [Kersting 2006]. W. Kersting, Distribution system modeling and analysis. CRC, 2006 24

Carnegie Mellon The End Thank You! Q&A 25