Caractersticas de las distribuciones estadsticas Nazira Calleja Estadstica

Características de las distribuciones estadísticas Nazira Calleja

Estadística Propósito del análisis estadístico Poner orden en el caos para: Comunicar de manera clara y concisa un conjunto de datos. Obtener bases para la toma de decisiones.

Distribución de datos

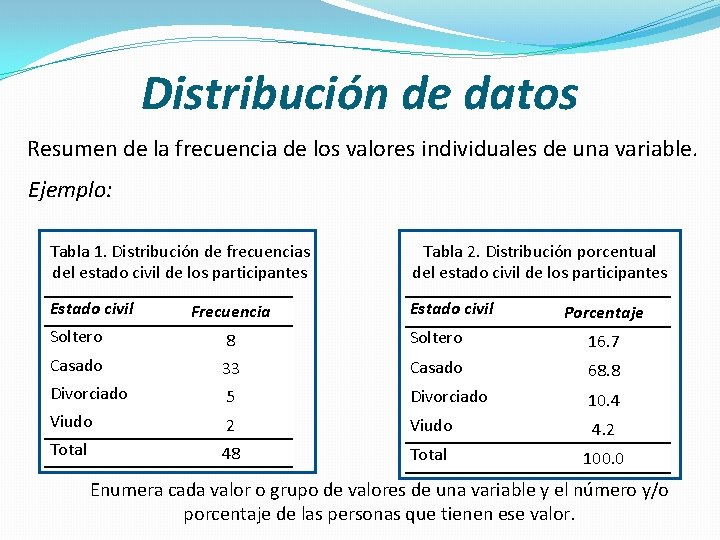
Distribución de datos Resumen de la frecuencia de los valores individuales de una variable. Ejemplo: Tabla 1. Distribución de frecuencias del estado civil de los participantes Tabla 2. Distribución porcentual del estado civil de los participantes Estado civil Frecuencia Porcentaje Soltero 8 Soltero 16. 7 Casado 33 Casado 68. 8 Divorciado 5 Divorciado Viudo 10. 4 2 Viudo Total 4. 2 48 Total 100. 0 Enumera cada valor o grupo de valores de una variable y el número y/o porcentaje de las personas que tienen ese valor.

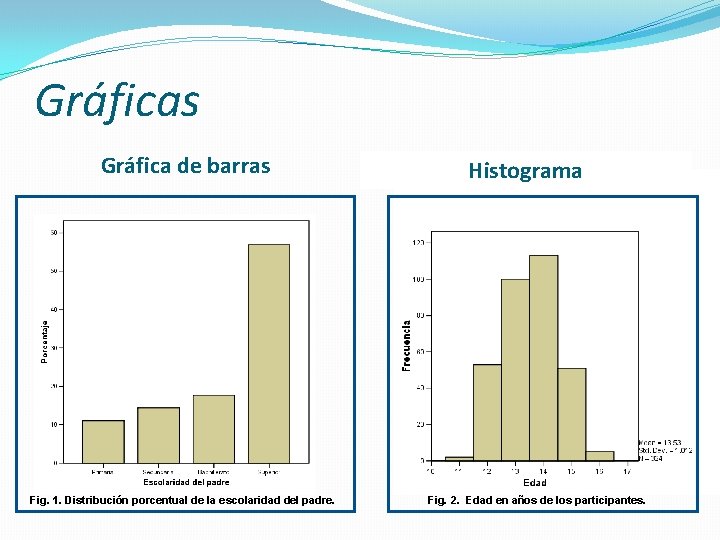
Gráficas Gráfica de barras Fig. 1. Distribución porcentual de la escolaridad del padre. Histograma Fig. 2. Edad en años de los participantes.

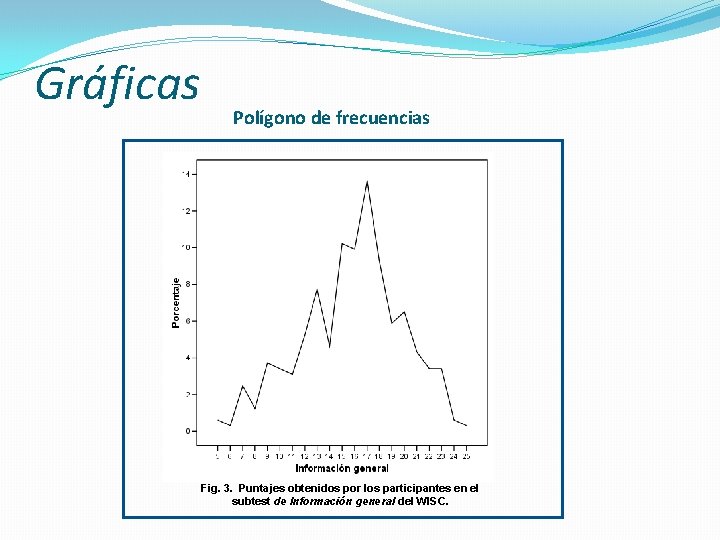
Gráficas Polígono de frecuencias Fig. 3. Puntajes obtenidos por los participantes en el subtest de Información general del WISC.

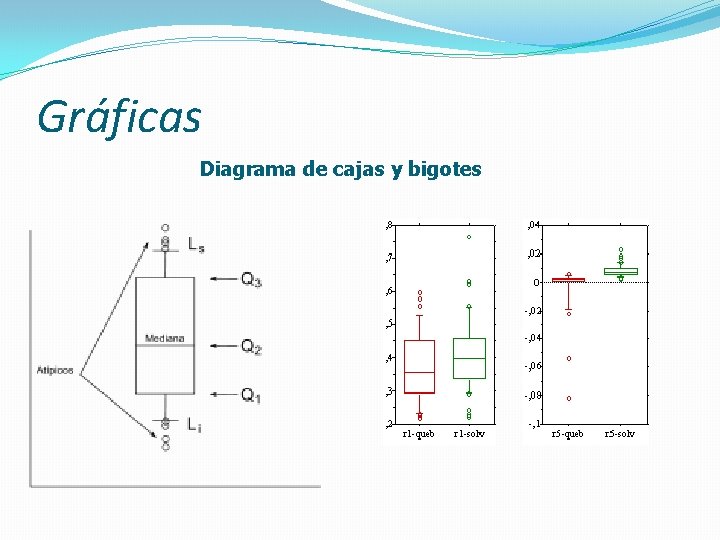
Gráficas Diagrama de cajas y bigotes

Medidas descriptivas

Medidas descriptivas Medidas de síntesis: Índices Indican valores con respecto a Modo Tendencia central los que los datos parecen Mediana agruparse Media Rango Indican la mayor o menor Rango semiintercuartilar concentración de los datos con Dispersión Desviación estándar respecto a las medidas de Varianza tendencia central Coeficiente de variación Posición Dividen un conjunto ordenado Cuartiles de datos en grupos con la Deciles misma cantidad de individuos Percentiles Forma Comparan la forma que tiene Asimetría o sesgo la representación gráfica con la Curtosis o apuntamiento distribución normal.

Población y muestra POBLACIÓN MUESTRA El universo de todos los casos Parámetros Un subconjunto de una población Estadísticos Letras griegas ( , , ) Letras latinas ( , s, r).

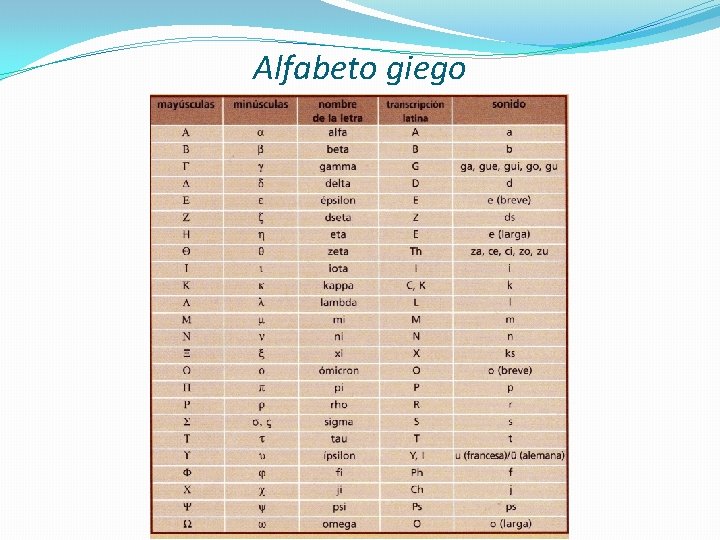
Alfabeto giego

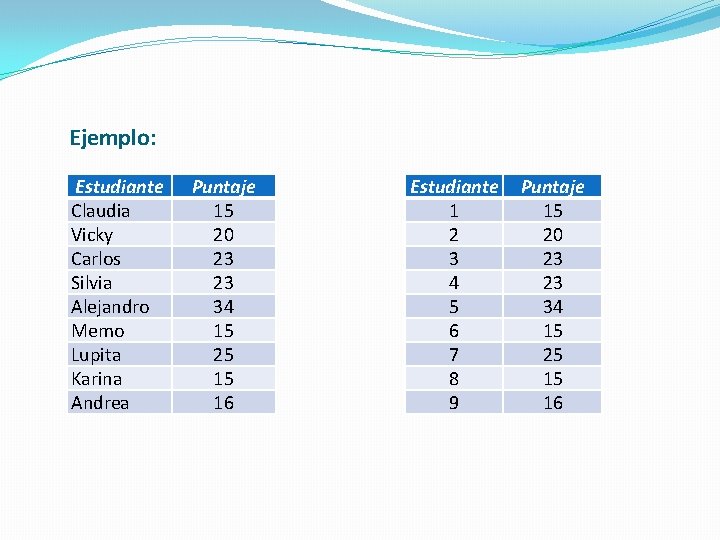
Ejemplo: Estudiante Claudia Vicky Carlos Silvia Alejandro Memo Lupita Karina Andrea Puntaje 15 20 23 23 34 15 25 15 16 Estudiante 1 2 3 4 5 6 7 8 9 Puntaje 15 20 23 23 34 15 25 15 16

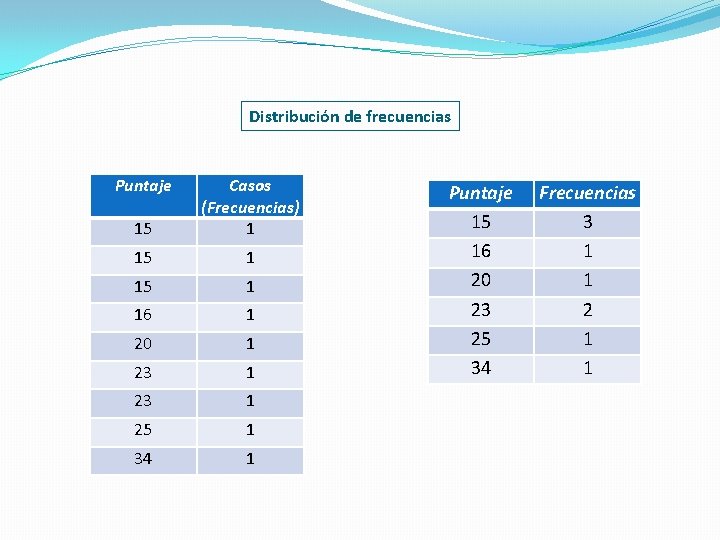
Distribución de frecuencias Puntaje 15 Casos (Frecuencias) 1 15 1 16 1 20 1 23 1 25 1 34 1 Puntaje 15 16 20 23 25 34 Frecuencias 3 1 1 2 1 1

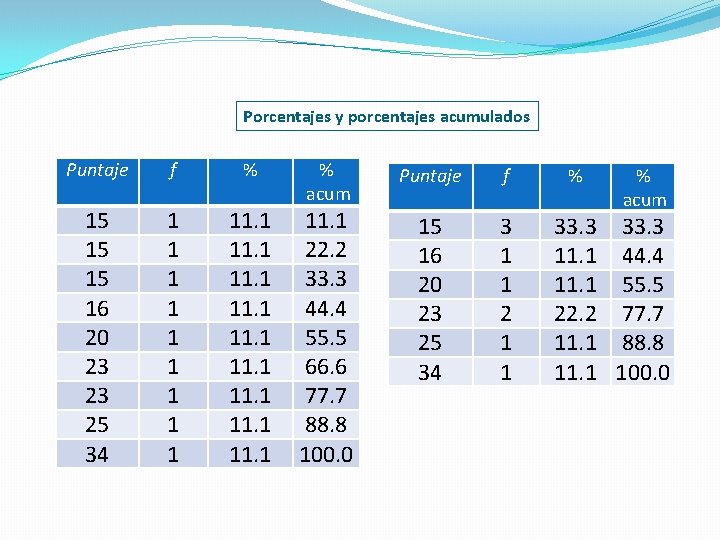
Porcentajes y porcentajes acumulados Puntaje f % 15 15 15 16 20 23 23 25 34 1 1 1 1 11. 1 % acum 11. 1 22. 2 33. 3 44. 4 55. 5 66. 6 77. 7 88. 8 100. 0 Puntaje f 15 16 20 23 25 34 3 1 1 2 1 1 % % acum 33. 3 11. 1 44. 4 11. 1 55. 5 22. 2 77. 7 11. 1 88. 8 11. 1 100. 0

Medidas de tendencia central

Medidas de tendencia central Estimación del "centro" de una distribución de valores. • Modo • Mediana • Media SPSS: Analizar – Estadísticos descriptivos – Frecuencias - Estadísticos

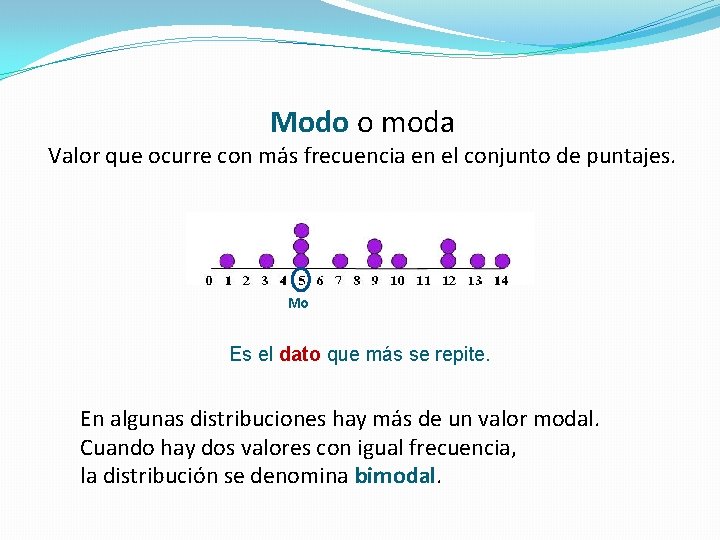
Modo o moda Valor que ocurre con más frecuencia en el conjunto de puntajes. Mo Es el dato que más se repite. En algunas distribuciones hay más de un valor modal. Cuando hay dos valores con igual frecuencia, la distribución se denomina bimodal.

Modo o moda: Valor que ocurre con más frecuencia en el conjunto de puntajes. Cómputo: Enlistar todos los puntajes en orden numérico y contar el número de casos en cada puntaje. Mo = 15 Modo Puntaje 15 16 20 23 25 34 f 3 1 1 2 1 1

Mediana Puntaje que se encuentra exactamente en el centro del conjunto de valores. 10 12 14 16 18 20 22 Mdn = 16 Md Me Mdn Es el dato que ocupa la posición central en un conjunto ordenado de datos.

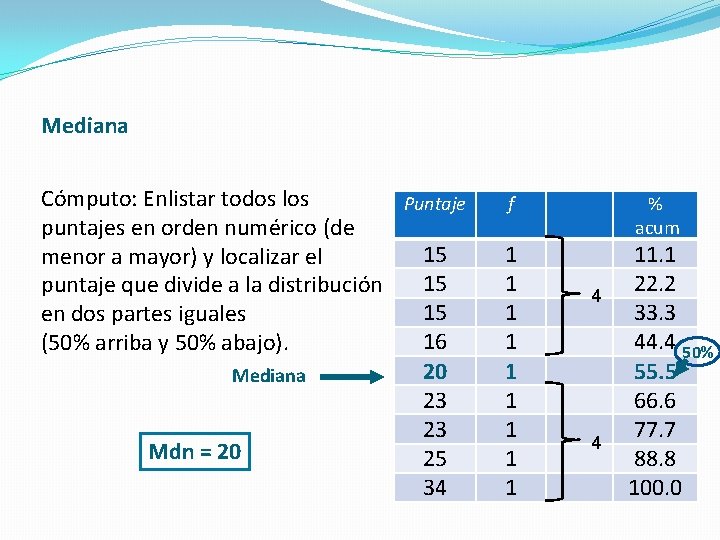
Mediana Cómputo: Enlistar todos los Puntaje puntajes en orden numérico (de 15 menor a mayor) y localizar el 15 puntaje que divide a la distribución 15 en dos partes iguales 16 (50% arriba y 50% abajo). 20 Mediana 23 23 Mdn = 20 25 34 f 1 1 1 1 1 % acum 4 4 11. 1 22. 2 33. 3 44. 4 50% 55. 5 66. 6 77. 7 88. 8 100. 0

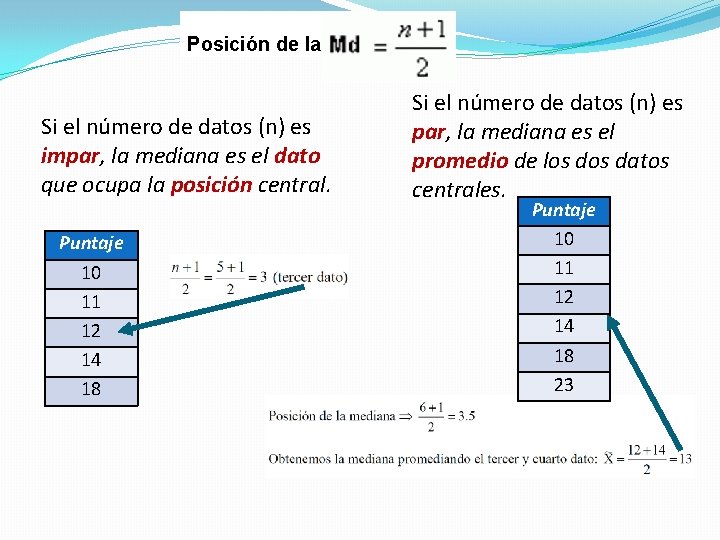
Posición de la Si el número de datos (n) es impar, la mediana es el dato que ocupa la posición central. Puntaje 10 11 12 14 18 Si el número de datos (n) es par, la mediana es el promedio de los datos centrales. Puntaje 10 11 12 14 18 23

Media o promedio Cómputo: sumar los puntajes y dividirles entre el número de casos. Ejemplo: Puntajes obtenidos por 9 estudiantes en un examen: Media = 186 / 9 = 20. 66 Estudiante 1 2 3 4 5 6 7 8 9 Suma Puntaje 15 20 23 23 34 15 25 15 16 186

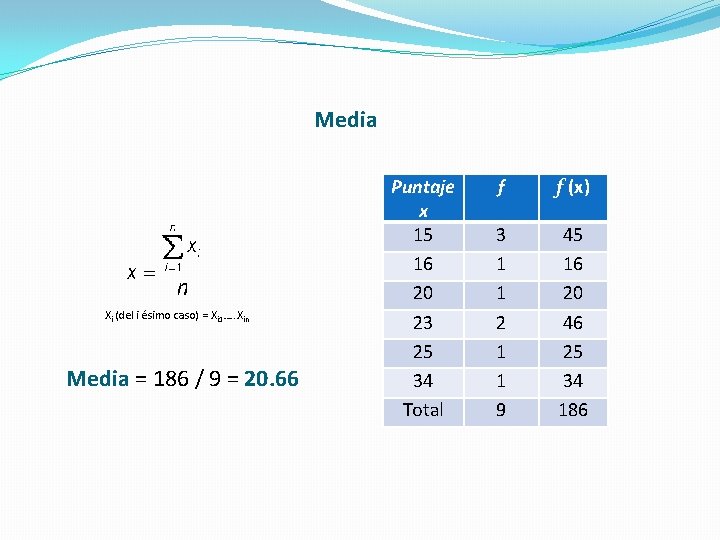
Media Xi (del i ésimo caso) = Xi 1…. . Xin Media = 186 / 9 = 20. 66 Puntaje x 15 16 20 23 25 34 Total f f (x) 3 1 1 2 1 1 9 45 16 20 46 25 34 186

Medidas de dispersión

Medidas de dispersión Dispersión Variabilidad de los valores alrededor de la tendencia central. � Rango intercuartilar � Varianza � Desviación estándar � Coeficiente de variación SPSS: Analizar – Estadísticos descriptivos – Frecuencias - Estadísticos

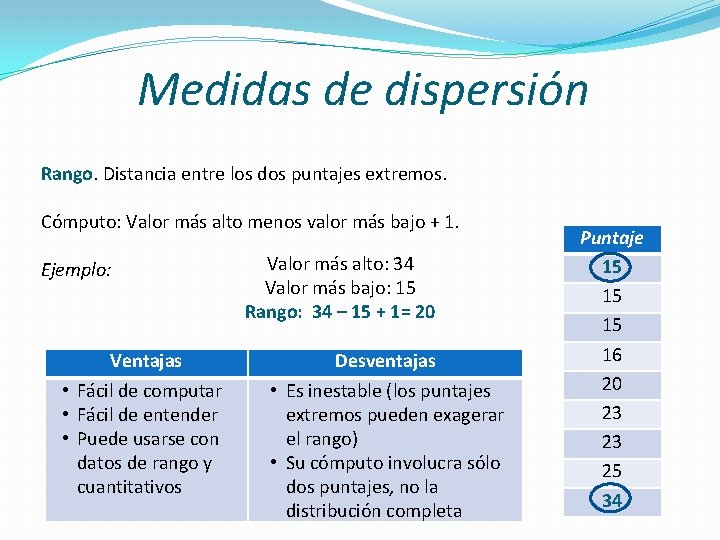
Medidas de dispersión Rango. Distancia entre los dos puntajes extremos. Cómputo: Valor más alto menos valor más bajo + 1. Ejemplo: Ventajas • Fácil de computar • Fácil de entender • Puede usarse con datos de rango y cuantitativos Valor más alto: 34 Valor más bajo: 15 Rango: 34 – 15 + 1= 20 Desventajas • Es inestable (los puntajes extremos pueden exagerar el rango) • Su cómputo involucra sólo dos puntajes, no la distribución completa Puntaje 15 15 15 16 20 23 23 25 34

Desviación estándar: �Medida de dispersión más exacta y detallada. �Muestra la relación que un grupo de valores tiene con la media. �Es la distancia promedio de los puntajes con respecto a la media. �Ayuda a crear una representación más exacta de la distribución Desviación estándar pequeña Grupo de datos donde los puntajes están muy cerca del valor de la media; existe poca variación; corresponde a un rango pequeño Desviación estándar grande Grupo de datos con más variación; gran diferencia entre los puntajes; corresponde a un rango grande

�Cálculo S = desviación estándar Σ = suma de X = puntaje individual M = media de todos los puntajes n = tamaño de la muestra (número de puntajes) [n-1 porque se calcula para una muestra, no para la población] Ejemplo: En una distribución con una media de 80 y una desviación estándar de 10, la dispersión será mucho mayor que si la desviación es de 2.

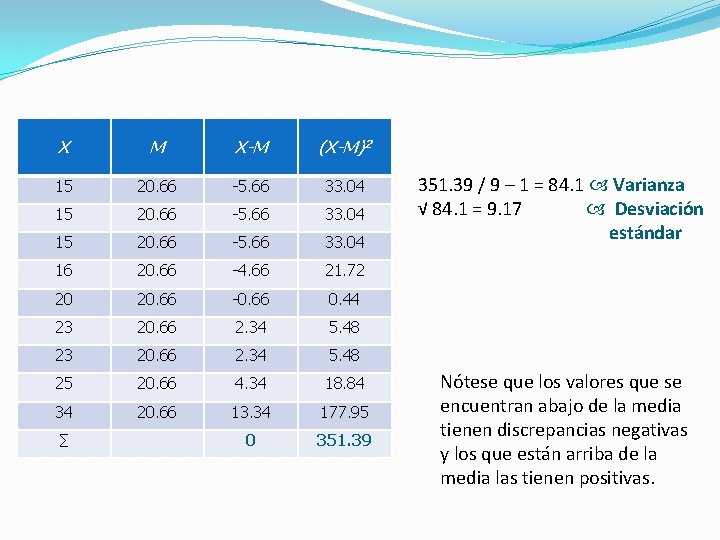
X M X-M (X-M)2 15 20. 66 -5. 66 33. 04 16 20. 66 -4. 66 21. 72 20 20. 66 -0. 66 0. 44 23 20. 66 2. 34 5. 48 25 20. 66 4. 34 18. 84 34 20. 66 13. 34 177. 95 0 351. 39 ∑ 351. 39 / 9 – 1 = 84. 1 Varianza √ 84. 1 = 9. 17 Desviación estándar Nótese que los valores que se encuentran abajo de la media tienen discrepancias negativas y los que están arriba de la media las tienen positivas.

Medidas de posición

Medidas de posición � Cuartiles � Deciles � Centiles SPSS: Analizar – Estadísticos descriptivos – Frecuencias - Estadísticos

Medidas de posición Dividen un conjunto ordenado de datos en grupos con la misma cantidad de individuos. Cuartiles De la misma manera en que la mediana divide a la distribución en dos partes iguales (50% debajo de ese puntaje y 50% arriba), los cuartiles la dividen en cuatro partes iguales (del 25% cada una). Son tres y se denotan: Q 1, Q 2 y Q 3 La Mdn y el Q 2 coinciden en el mismo valor.

Medidas de posición Deciles Dividen a la distribución en diez partes iguales (del 10% cada una). Son 9 y e le denotan D 1, D 2, . . . , D 9. El decil 5 coincide con la Mdn en el mismo valor.

Centiles o percentiles Dividen a la distribución en cien partes iguales (del 1% cada una). Se utilizan en pruebas estandarizadas. Son 99 y se les denota P 1, P 2, . . . , P 99. El percentil 50 coincide con la Mdn, con el Q 2 y con el decil 5 en el mismo valor.

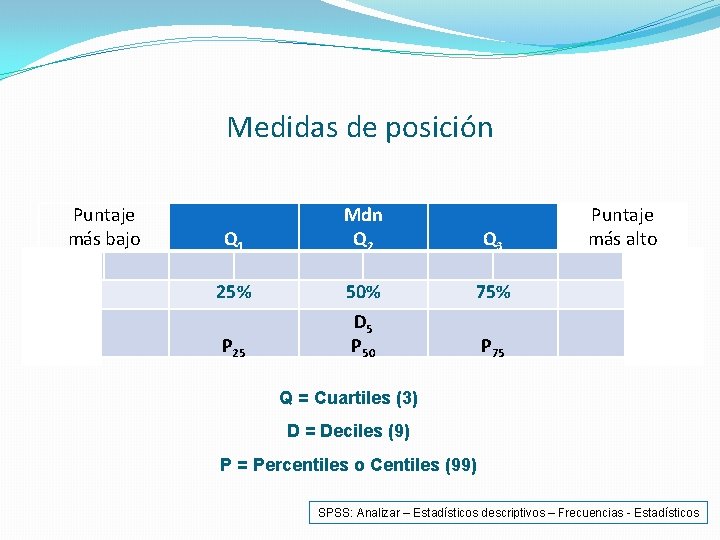
Medidas de posición Puntaje más bajo Q 1 25% P 25 Mdn Q 2 50% D 5 P 50 Q 3 Puntaje más alto 75% P 75 Q = Cuartiles (3) D = Deciles (9) P = Percentiles o Centiles (99) SPSS: Analizar – Estadísticos descriptivos – Frecuencias - Estadísticos

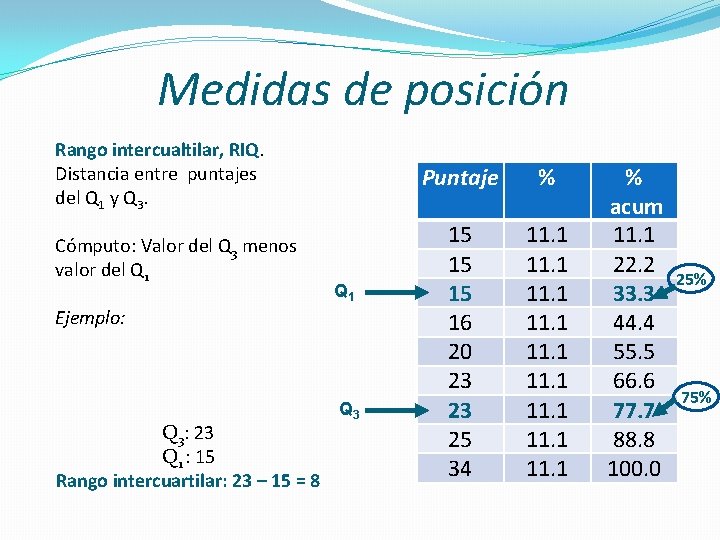
Medidas de posición Rango intercualtilar, RIQ. Distancia entre puntajes del Q 1 y Q 3. Cómputo: Valor del Q 3 menos valor del Q 1 Ejemplo: Q 3: 23 Q 1 : 15 Rango intercuartilar: 23 – 15 = 8 Q 3 Puntaje % 15 15 15 16 20 23 23 25 34 11. 1 11. 1 % acum 11. 1 22. 2 33. 3 44. 4 55. 5 66. 6 77. 7 88. 8 100. 0 25% 75%

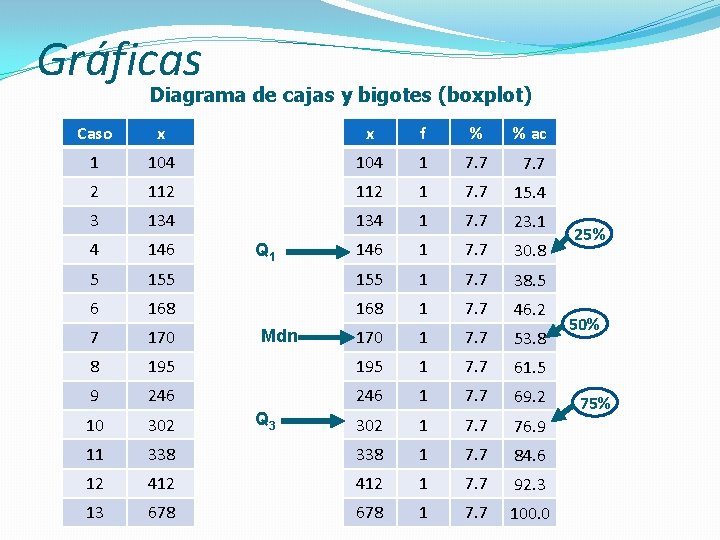
Gráficas Diagrama de cajas y bigotes (boxplot) Caso x x f % % ac 1 104 1 7. 7 112 1 7. 7 15. 4 134 1 7. 7 23. 1 146 1 7. 7 30. 8 2 3 112 Ejemplo: 134 4 146 5 155 1 7. 7 38. 5 6 168 1 7. 7 46. 2 7 170 1 7. 7 53. 8 8 195 1 7. 7 61. 5 9 246 1 7. 7 69. 2 10 302 1 7. 7 76. 9 11 338 1 7. 7 84. 6 12 412 1 7. 7 92. 3 13 678 1 7. 7 100. 0 Q 1 Mdn Q 3 25% 50% 75%

Gráficas Diagrama de cajas y bigotes (boxplot) Atípicos extremos: >Q 3 X 3 Atípicos medios: >Q 3 X 1. 5 y <Q 3 X 3 Límite superior: Q 3 X 1. 5 Rango intercuartilar (50% de la distribución) Límite inferior: Q 1 X 1. 5 Atípicos medios: <Q 1 X 1. 5 y >Q 1 X 3 Atípicos extremos: < Q 1 X 3

Gráficas Diagrama de cajas y bigotes (boxplot) Atípico extremo (outlier) Límite superior Q 1 Rango intercuartilar Mdn Q 3 Límite inferior SPSS: Gráficos - Interactivos

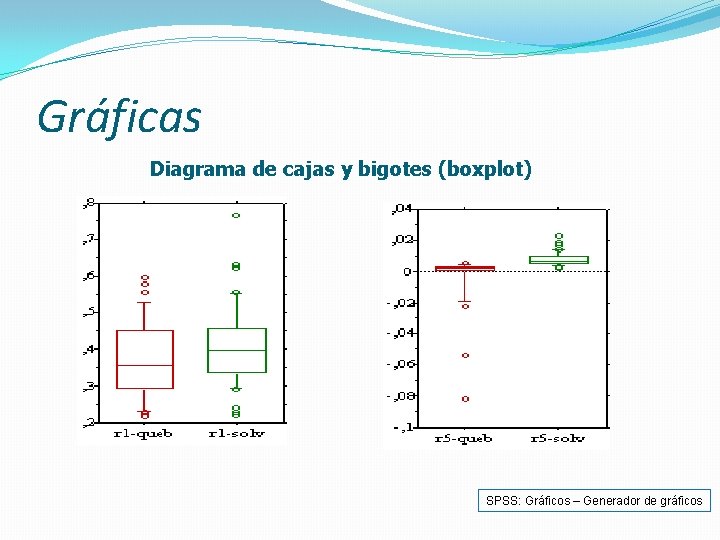
Gráficas Diagrama de cajas y bigotes (boxplot) SPSS: Gráficos – Generador de gráficos

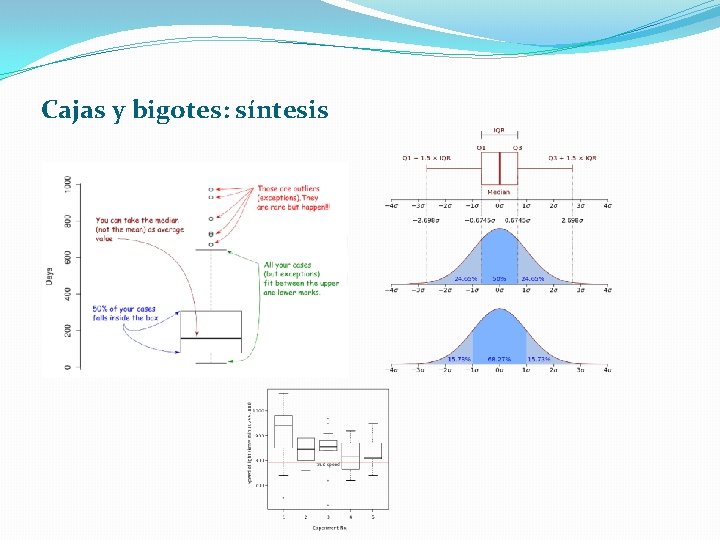
Cajas y bigotes: síntesis

Medidas de forma

Medidas de forma • Asimetría o sesgo • Curtosis SPSS: Analizar – Estadísticos descriptivos – Frecuencias - Estadísticos

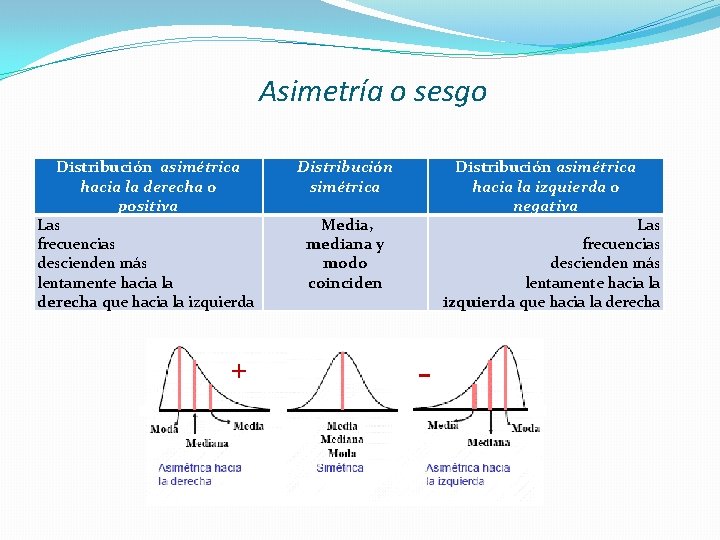
Asimetría o sesgo Distribución asimétrica hacia la derecha o positiva Las frecuencias descienden más lentamente hacia la derecha que hacia la izquierda + Distribución simétrica Distribución asimétrica hacia la izquierda o negativa Media, mediana y modo coinciden Las frecuencias descienden más lentamente hacia la izquierda que hacia la derecha -

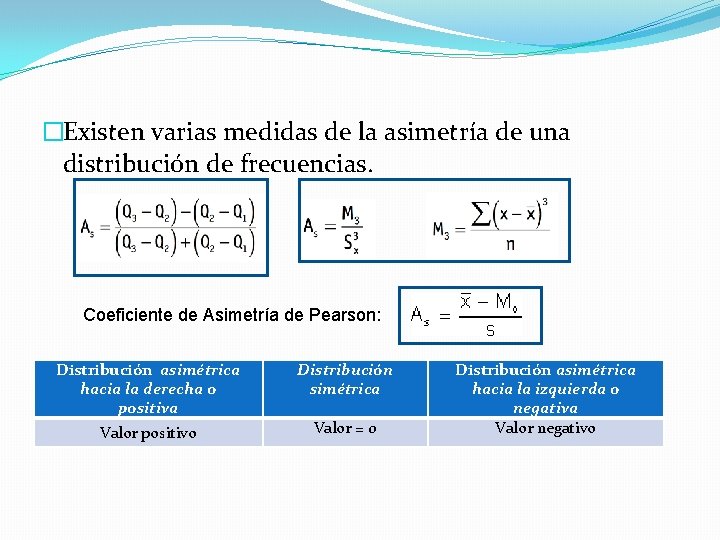
�Existen varias medidas de la asimetría de una distribución de frecuencias. Coeficiente de Asimetría de Pearson: Distribución asimétrica hacia la derecha o positiva Valor positivo Distribución simétrica Valor = 0 Distribución asimétrica hacia la izquierda o negativa Valor negativo

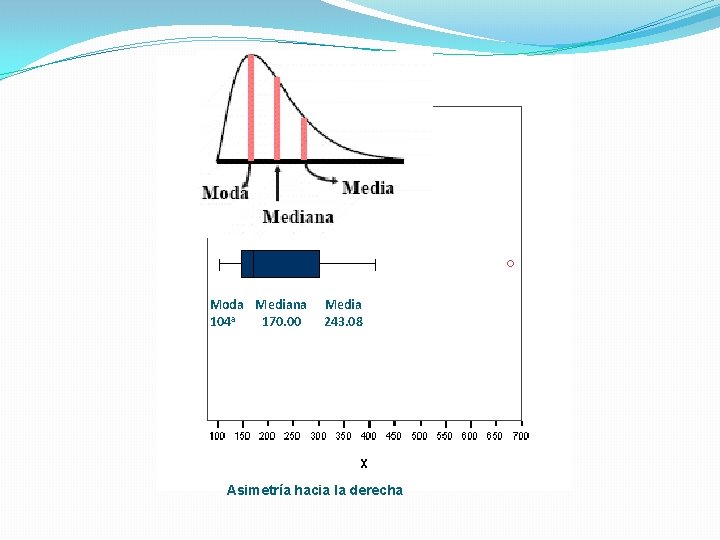
Moda Mediana 104 a 170. 00 Media 243. 08 Asimetría hacia la derecha

Curtosis Distribución leptocúrtica Distribución mesocúrtica Distribución platicúrtica Leptós significa 'fino', 'delgado', 'agudo' Mesós equivale a 'medio', 'mediano' Platýs es 'ancho, 'plano', 'liso' Presenta un elevado grado de concentración alrededor de los valores centrales de la variable Presenta un grado de concentración medio alrededor de los valores centrales de la variable + Presenta un reducido grado de concentración alrededor de los valores centrales de la variable -

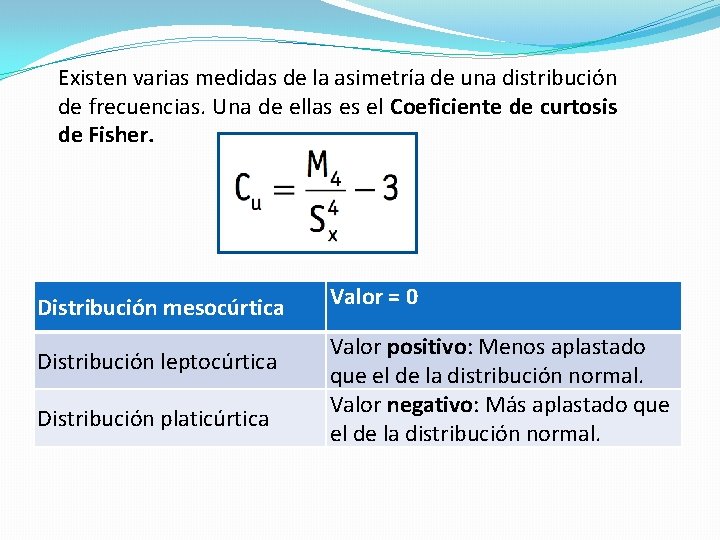
Existen varias medidas de la asimetría de una distribución de frecuencias. Una de ellas es el Coeficiente de curtosis de Fisher. Distribución mesocúrtica Distribución leptocúrtica Distribución platicúrtica Valor = 0 Valor positivo: Menos aplastado que el de la distribución normal. Valor negativo: Más aplastado que el de la distribución normal.