Captulo 1 Nmeros Racionais Fraes v Uma frao

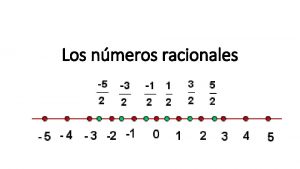
Capítulo 1: Números Racionais

Frações v Uma fração representa o quociente exato de dois números inteiros. numerador Lê-se: “dois terços” denominador É uma fração própria, porque representa um número : 5 menor do que um. Fração própria : 5 Fração irredutível : 2 É uma fração imprópria, porque representa um número : 2 maior do que um.

Numeral misto As frações superiores à unidade (frações impróprias) podem ser representadas sob a forma de uma adição ou sob a forma de numeral misto fraccionário. Para escrever uma fração sob a forma de numeral misto fraccionário: Para escrever um numeral misto na forma de fração:

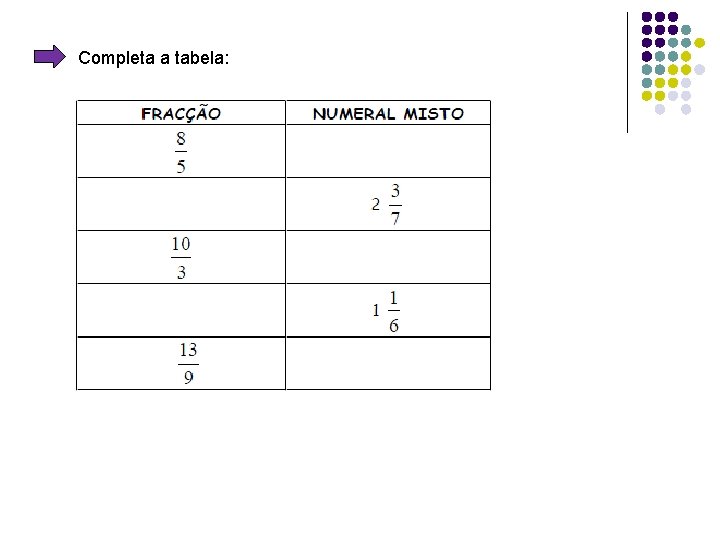
Completa a tabela:

Frações e Dízimas Por vezes, quando se dividem dois números, o quociente é exato e é um número inteiro. 3 é o quociente exacto de 15 por 5 logo é um número inteiro.

Outras vezes, quando se dividem dois números, o quociente é exato e é um número decimal. 0, 75 é o quociente exato de 3 por 4 logo é uma fração equivalente a uma fração decimal que corresponde a uma dízima finita. Outras vezes, quando se dividem dois números, o quociente exato não é um número inteiro nem decimal. 0, 3333 não é o quociente exato de 1 por 3. A única forma de representar o quociente exato de 1 por 3 é na forma de fração. É um fração não equivalente a uma fração decimal

v Uma fração não equivalente a uma fração decimal corresponde a uma dízima infinita periódica de período 3 dízima infinita periódica de período 285714 dízima infinita periódica de período 09 No entanto, há números que não correspondem a dizimas finitas nem infinitas periódicas: dízima infinitas não periódicas (não tem uma sequência de números que se repita)

Conjuntos Numéricos = {números naturais} = {1, 2, 3, 4, …} = { números inteiros relativos} = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …} = {números racionais} Número racional é todo o número que se pode escrever como quociente de números inteiros, com divisor diferente de zero, ou seja, é aquele que pode ser representado por uma dízima finita ou uma dízima infinita periódica.

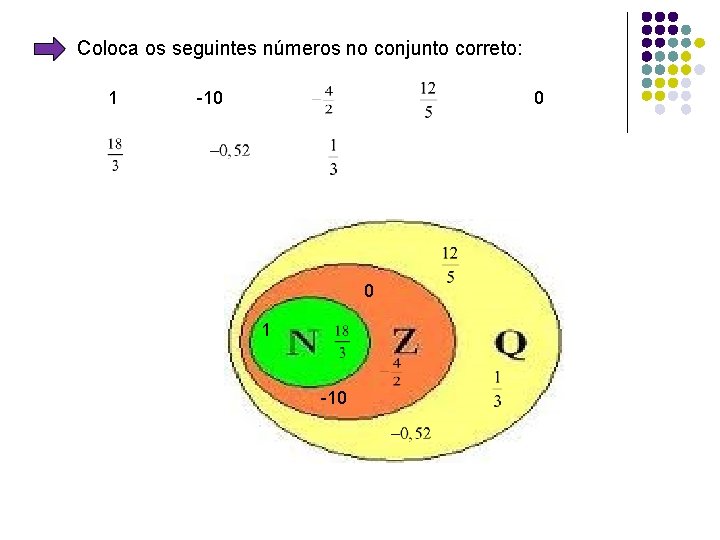
Coloca os seguintes números no conjunto correto: 1 -10 0 0 1 -10

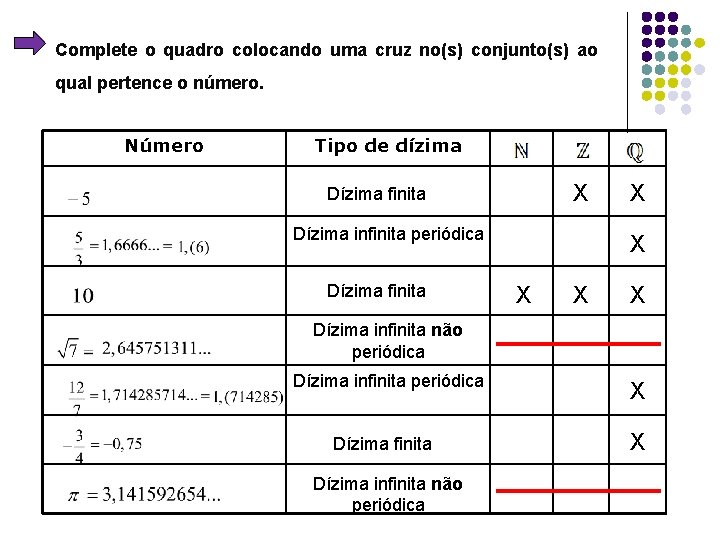
Complete o quadro colocando uma cruz no(s) conjunto(s) ao qual pertence o número. Número Tipo de dízima X Dízima finita Dízima infinita periódica Dízima finita X X X Dízima infinita não periódica Dízima infinita periódica Dízima finita Dízima infinita não periódica X X

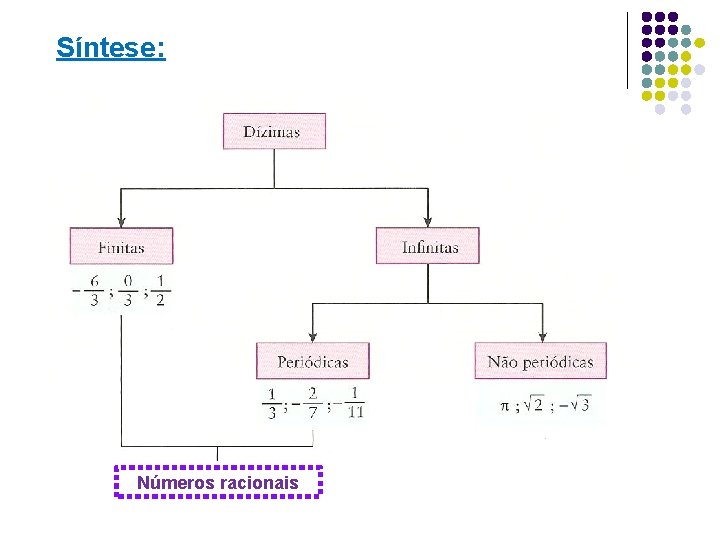
Síntese: Números racionais

Comparação de números racionais 1ª Situação: Comparar com 2, 0947: Então: 2, 0947 2ª Situação: Comparar 5<7 com : 3 > 2 mas como os números são negativos:

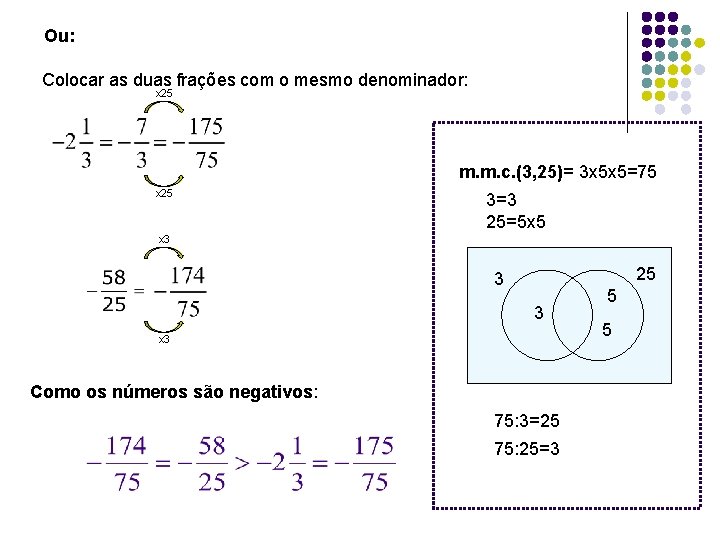
Ou: Colocar as duas frações com o mesmo denominador: x 25 m. m. c. (3, 25)= 3 x 5 x 5=75 x 25 3=3 25=5 x 5 x 3 25 3 3 x 3 Como os números são negativos: 75: 3=25 75: 25=3 5 5

Representação de números racionais § a abcissa do ponto P é -2 e representa-se por P -2 v Também é possível representar um número racional numa reta numérica: A -2, 5 B C Ordena as abcissas dos pontos por ordem crescente: D

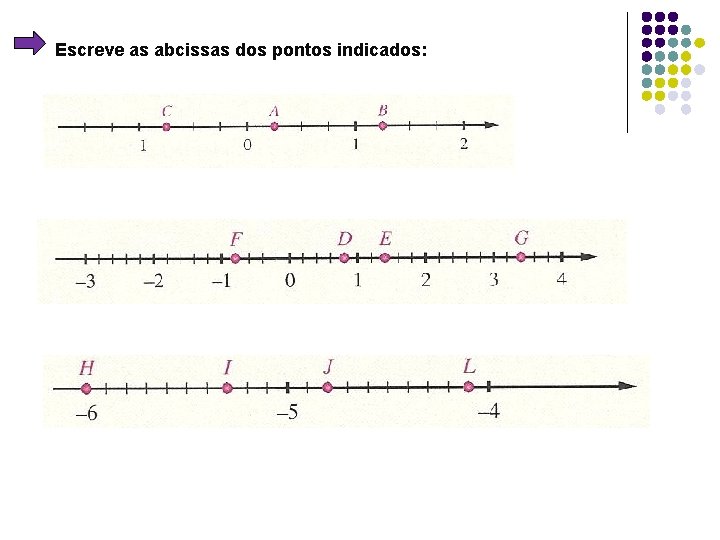
Escreve as abcissas dos pontos indicados:

Adição e Subtração de números racionais Simplificar a escrita desembaraçando de parêntesis 1º Processo: “devo 2, 6 tenho 1, 56”. 2, 6 -1, 56 “fico então ainda a dever” 1, 0 4 1

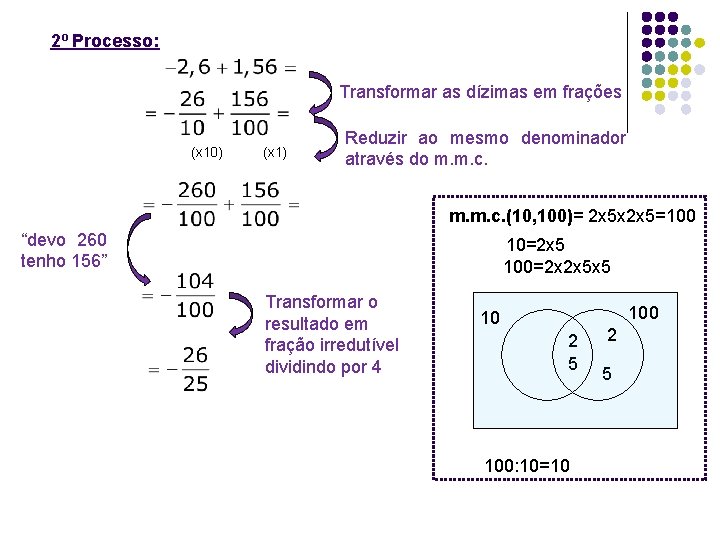
2º Processo: Transformar as dízimas em frações (x 10) (x 1) Reduzir ao mesmo denominador através do m. m. c. (10, 100)= 2 x 5 x 2 x 5=100 “devo 260 tenho 156” 10=2 x 5 100=2 x 2 x 5 x 5 Transformar o resultado em fração irredutível dividindo por 4 100 10 2 5 100: 10=10 2 5

Calcula o valor numérico da expressão: Desembaraçar de parêntesis Transformar as dízimas em frações (x 10) (x 3) : 3 (x 5) (x 10) Reduzir ao mesmo denominador através do m. m. c.

Problema: Ao pequeno-almoço uma família bebe regularmente leite. Num certo dia registou-se o seguinte: • o pai bebeu de litro de leite; • a mãe bebeu de litro de leite; • a Inês bebeu de litro de leite; • o João bebeu de litro de leite; a) Escreve uma expressão que represente a parte do leite que beberam os pais? b) Calcula a parte do leite que a Inês bebeu a mais do que o irmão João? (x 2) (x 1) R: A Inês bebeu mais de litro de leite do que o João.

c) Calcula o valor da seguinte expressão interpreta o resultado no contexto do problema. (x 40) R: (x 8) (x 10) (x 5) representa a parte de litro de leite que sobrou. e

Multiplicação de números racionais Para multiplicar dois números representados por frações multiplicam-se os numeradores e multiplicam-se os denominadores Transformar a dízima em fração Multiplicação de números com: • Sinais iguais • Sinais diferentes + -

Divisão de números racionais Para dividir dois números racionais, multiplica-se o dividendo pelo inverso do divisor. passa a x Inverso do divisor passa a x Transformar a dízima em fração Inverso do divisor

Expressões numéricas com números racionais (x 6) (x 1)

No cálculo de uma expressão numérica, habitualmente, seguem-se os seguintes passos: 1º Efetuam-se as operações dentro de parêntesis; 2º A multiplicação e a divisão têm prioridade sobre a adição e a subtração. 3º Sempre que na expressão numérica apareçam operações de multiplicação e divisão, estas devem-se efetuar pela ordem indicada; 4º Quando a expressão só tiver adições e subtrações, primeiro tiram-se os parêntesis e depois efetuam-se essas operações.

Problema: Um padeiro utiliza pequenos. Com de um saco de farinha de 75 kg para fazer pães do resto da farinha confecionou bolos. Posteriormente com a farinha que sobra distribui por saquinhos de kg. a) Calcula a quantidade de farinha utilizada para os pães pequenos. R: A quantidade de farinha utilizada para os pães foi de 25 kg. b) Calcula a quantidade de farinha utilizada para os bolos. Farinha que sobrou para os bolos R: A quantidade de farinha utilizada nos bolos foi de 12, 5 kg.

c) Quantos saquinhos de farinha conseguiu fazer? R: Consegue fazer 150 saquinhos de kg.

Potências de um número racional “Menos três ao cubo” ou “O cubo de menos três” “Menos dois terços ao quadrado” ou “O quadrado de menos dois terços ” Para passar o expoente a positivo faz-se o inverso da base

Relembrando: v Qualquer número, diferente de zero, elevado a zero é sempre um. v v Uma potência de base negativa e expoente par representa um número positivo. Exemplo: v Uma potência de base negativa e expoente ímpar representa um número negativo. Exemplo: v Uma potência de base positiva, independentemente do expoente, representa sempre um número positivo. Exemplos:

No cálculo de uma expressão numérica com potências, habitualmente, seguem-se os seguintes passos: 1º Calculam-se o valor das potências depois de ter aplicado as regras operatórias das mesmas; 2º Efetuam-se as operações dentro de parêntesis; 3º A multiplicação e a divisão têm prioridade sobre a adição e a subtração. 4º Sempre que na expressão numérica apareçam operações de multiplicação e divisão, estas devem-se efetuar pela ordem indicada; 5º Quando a expressão só tiver adições e subtrações, primeiro tiram-se os parêntesis e depois efectuam-se essas operações.

Expressões numéricas com potências de números racionais (x 8) (x 9) (x 8)

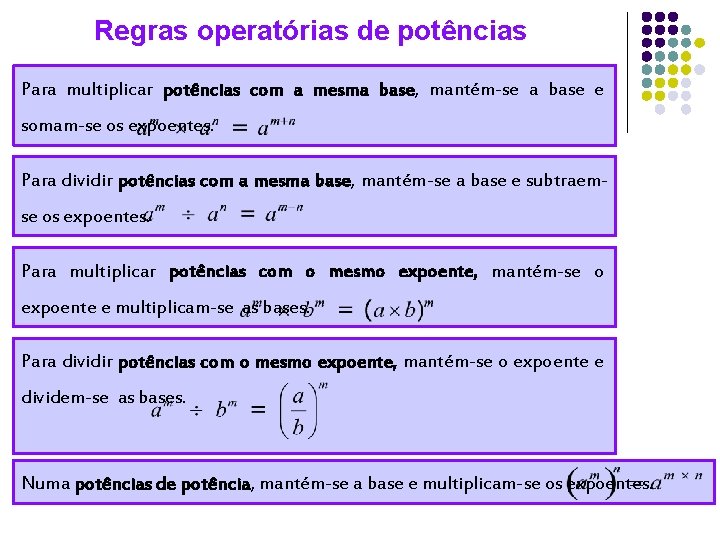
Regras operatórias de potências Para multiplicar potências com a mesma base, mantém-se a base e somam-se os expoentes. Para dividir potências com a mesma base, mantém-se a base e subtraemse os expoentes. Para multiplicar potências com o mesmo expoente, mantém-se o expoente e multiplicam-se as bases. Para dividir potências com o mesmo expoente, mantém-se o expoente e dividem-se as bases. Numa potências de potência, mantém-se a base e multiplicam-se os expoentes.

Exercício: a) j) b) k) c) l) d) m) e) n) f) o) g) p) h) i) q) r)

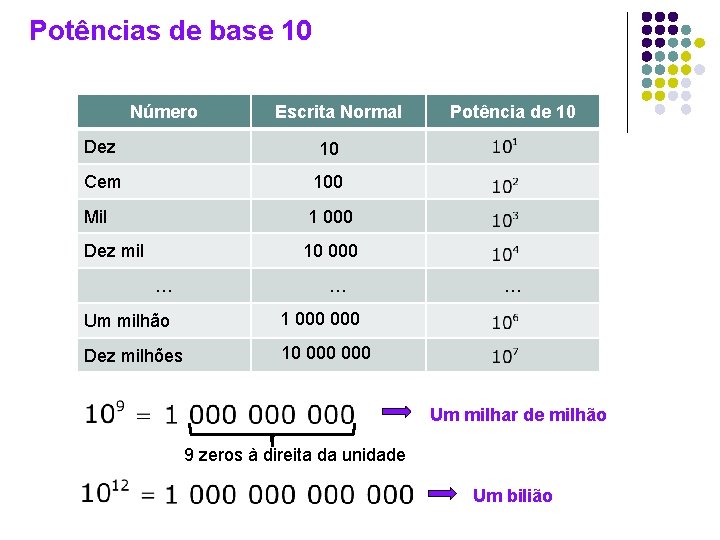
Potências de base 10 Número Escrita Normal Dez 10 Cem 100 Mil 1 000 Dez mil 10 000 … … Um milhão 1 000 Dez milhões 10 000 Potência de 10 … Um milhar de milhão 9 zeros à direita da unidade Um bilião

Classes: Unidades Milhares Milhões Milhares de milhão Bilião Milhares de bilião Trilião Milhares de trilião … Nota Importante: Um milhão Um bilião Um trilião 18 zeros Um quatrilião 24 zeros Um quintilião 30 zeros …

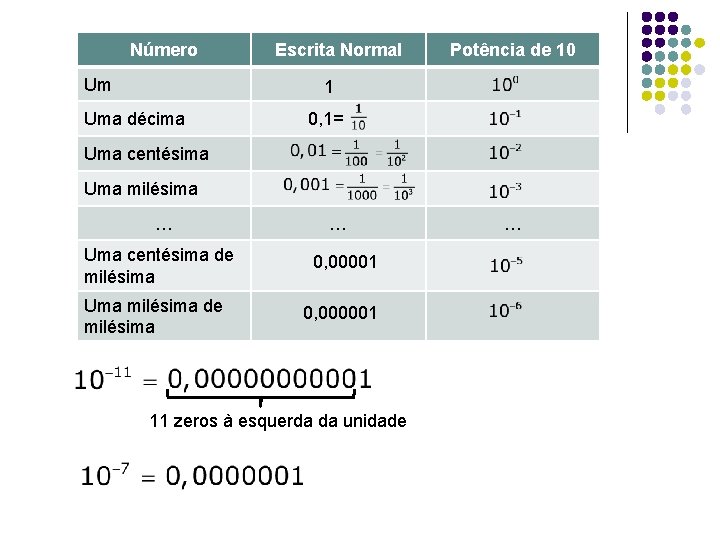
Número Um Escrita Normal Potência de 10 1 Uma décima 0, 1= Uma centésima Uma milésima … Uma centésima de milésima Uma milésima de milésima … 0, 00001 0, 000001 11 zeros à esquerda da unidade …

A vírgula deslocou-se 7 casas para a direita A vírgula deslocou-se 5 casas para a esquerda Se multiplicarmos qualquer número decimal por uma potência de 10 com expoente positivo, a vírgula desloca-se para a direita tantas casas quanto o valor absoluto do expoente. Se multiplicarmos qualquer número decimal por uma potência de 10 com expoente negativo, a vírgula desloca-se para a esquerda tantas casas quanto o valor absoluto do expoente.

Notação Científica Um número positivo está escrito em notação científica se tem a forma , onde a um e é um número inteiro ou decima menor que 10 e maior ou igual é um número inteiro. Na calculadora:

Vantagens: v Os números muito grandes ou muito pequenos podem ser escritos de forma mais abreviada. v Facilita a comparação de números muito grandes ou muito pequenos. v Tornam os cálculos muito mais simples e rápidos.

Comparação de números em notação científica: Distância ao Sol (em Km) Mercúrio Vénus Terra As potências de base 10 têm o mesmo expoente mas 1, 1 < 1, 5 O expoente (7) da potência de base 10 do primeiro número é inferior ao do segundo (8) Para compararmos números escritos em notação científica: Ø Se as potências de base 10 têm expoentes diferentes, é maior o número cuja potência de base 10 tiver expoente maior; Ø Se as potências de base 10 têm expoentes iguais, é maior o número cujo fator entre 1 e 10 for superior.

Notação Científica e Operações Multiplicação: Colocar os nºs em notação científica Aplica-se a propriedade comutativa da multiplicação Escreve-se a resposta em notação científica Exemplo: Um ano-luz (a. l. ) equivale a km. O horizonte do Universo observável dista da Terra. Escreve esta distância em km.

Divisão: Exemplo: Em Química, calcula-se, aproximadamente, a massa (em g) de um átomo de ouro, dividindo por. Qual é, aproximadamente, a massa de um átomo de ouro? R: Um átomo de ouro tem aproximadamente a massa de g.

Sistematizando:

Adição e Subtação: Colocar as potências de 10 com o mesmo expoente Aplica-se a propriedade distributiva Escreve-se a resposta em notação científica

Exemplo: Calcula a diferença, em kg, entre a massa de um átomo de lítio e a massa de um átomo de hidrogénio. Átomo Massa (kg) Lítio Hidrogénio R: Um átomo de lítio tem mais kg que um átomo de hidrogénio.