CAPM I Correlations between stocks Introducing risk of

CAPM I: Correlations between stocks Introducing risk of a stock portfolio The math behind diversification and risk

Random walks n n If you have studied a lot of probability theory, you probably know what a random walk is If you are not familiar with random walks, I will give you a five-minute guide n This is very simplified and not meant to be a rigorous analysis of random walks

Example: A simple random walk n n n It’s 3 am on DP on Halloween night Someone has had too much to drink and is trying to walk home without passing out Due to the lack of sobriety, every step taken is a step to the left or right n This person never walks straight n n 50/50 probability of going left/right What does this look like?

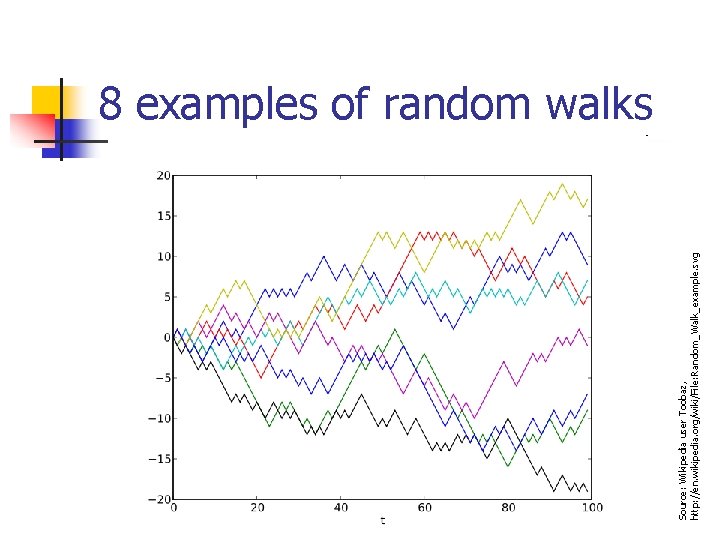
Source: Wikipedia user Toobaz, http: //en. wikipedia. org/wiki/File: Random_Walk_example. svg 8 examples of random walks

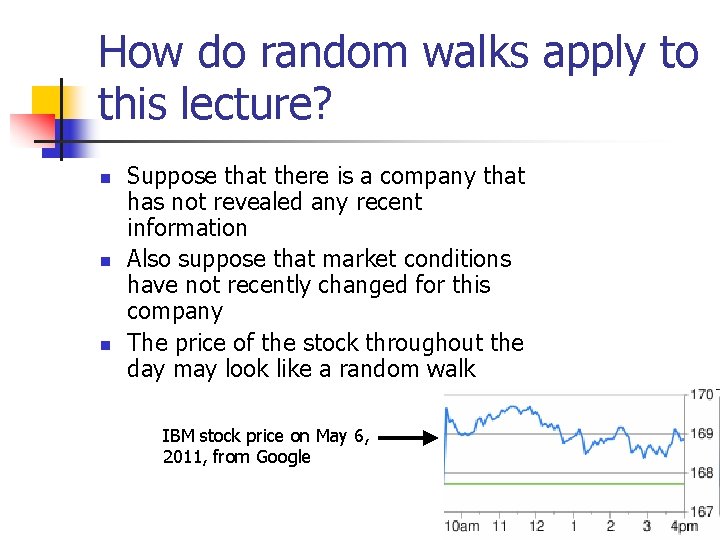
How do random walks apply to this lecture? n n n Suppose that there is a company that has not revealed any recent information Also suppose that market conditions have not recently changed for this company The price of the stock throughout the day may look like a random walk IBM stock price on May 6, 2011, from Google

The random walk hypothesis n Stocks fluctuate up and down like a random walk n n Recall that the previous movements of a stock have no impact on future movements if this hypothesis is true If potential movements in the stock’s price are symmetric in probabilities, we would have the expected future value at any point in time to be the same as the price now

Some do not believe the random walk hypothesis n Some people believe that trends in the stock market are predictable to a degree n n n If you can figure out how the past affects the future, you can buy and sell stocks in such a way as to profit What do you believe? n n n Past fluctuations can help to predict future stock prices Who thinks patterns can be figured out? Who thinks random walks explain better? More on random walk hypothesis in Chapter 14

CAPM n n The last lecture and today’s deal with CAPM What is CAPM? n n n Capital Asset Pricing Model Wikipedia defines it as a model that “is used to determine a theoretically appropriate required rate of return of an asset, if that asset is to be added to an already well-diversified portfolio, given that asset's non -diversifiable risk” Today, we address how we derive CAPM n But first, we want to understand the year 2008 better Wikipedia quote from http: //en. wikipedia. org/wiki/Capital_asset_pricing_model

2008 n n The years 1929 and 2008 will remain years of stock market crashes in people’s minds for centuries 2008 figures n n 37% decrease in stock prices for the year 16. 8% drop just in October

2008: Long-term bonds n When stock prices plummet, many people believe that the risk is too high for the potential reward n n Many people move money from stocks to bonds Price of stocks goes down n Dow Jones as low as 6, 458. 07 on March 9, 2009 Dow Jones is at almost 22, 000 at the beginning of August 2017 Price of long-term bonds goes up n These bondholders benefit from the stock market crash

2008: Other countries n “When the United States sneezes, the world catches a cold” n n An old saying about how much the United States impacts the rest of the world Many other countries’ stock markets are closely tied to US performance n China, India, Russia, and Iceland all experienced drops of >50% in 2008

Iceland n n n Population: ~320, 000 Before the US market crashed, three banks had debt ~6 times the country’s GDP This helped to contribute to a 90% loss in the country’s stock market in 2008 n n Little recovery to the stock market since the crash Due to this crisis, the nation’s currency, the króna, quickly lost more than two-thirds of it value, before stabilizing n n Early 2008: ~95 krónur per euro Early 2012: ~160 krónur per euro

Was the US on a long winning streak before 2008? n From 1942 to 2007, the United States looks like it had a very good times on average n n n Will this always happen? n n n Few years with negative returns No huge stock market crash No 2008 was a sign that despite a government’s best wishes to prevent market crashes, we cannot guarantee that crashes will not happen How can we get a better understanding of risk? We will expand our analysis of stocks n We will see if we can diversify to keep returns high while lowering risk at the same time

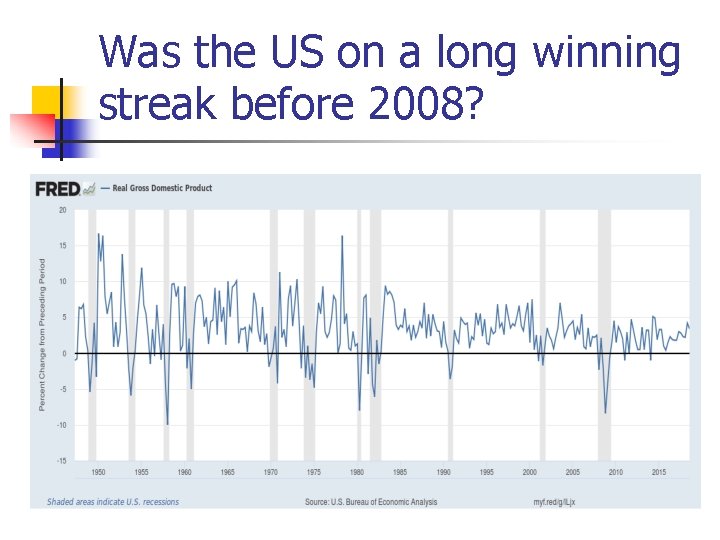
Was the US on a long winning streak before 2008?

Stock portfolios: An introduction n A stock portfolio is a set of two or more stocks that a person holds n n Portfolios could include more than stocks, such as bonds, precious metals, and cash Can stock portfolios help us to reduce overall risk while keeping expected return high?

Eliminating risk n In an ideal world, we would like two risky stocks that have the following characteristics n n High expected returns When one stock has lower-than-expected returns, the other stock has higher-thanexpected returns such that we are guaranteed our high rate of return

Eliminating risk: An example n Suppose that I have two stocks, priced at $100 each n n n Stock A: Expected return of 10% with risk Stock B: Expected return of 10% with risk Assume that Stock A goes up by W% this year n To eliminate risk, Stock B will have to go up by (20 – W )% this year

Numerical example n Stocks A and B both sell for $100 today n n Expected return of 10% for both stocks Suppose that Stock A goes up by $5 this year n Stock B will need to go up by $15 this year to get the 10% return guaranteed to eliminate annual risk n (5 + 15) / 200 = 10%

In the real world n n In the real world, there is no perfect set of stocks that we can buy that guarantees us a constant positive rate of return We can often find two different stocks such that when one stock has less-thanaverage returns, the other is likely to have more-than-average returns

Understanding interaction between two stocks n Covariance and correlation coefficients n n These measures tell us how returns of two different stocks are related to each other One nice feature about correlation coefficients n Normalized such that we always get a number between -1 and 1

Zero correlation/correlation coefficient n Stocks with no correlation on returns will have returns that are completely unrelated to each other

Positive values n When covariance or correlation is positive between two stocks, they tend to have higher-than-average returns at the same time more frequently than those stocks that are uncorrelated

Negative values n When covariance or correlation is negative between two stocks, they tend to have higher-than-average returns at different times more frequently than those stocks that are uncorrelated What about the math? Coming in the next lecture

Variance of a generic portfolio with two assets n n Let XA and XB be the proportions of the total portfolio in assets A and B, respectively Let A and B be the standard deviations of A and B, respectively Let A, B be the covariance between the two assets Recall that the correlation is between -1 and 1

Variance of a generic portfolio with two assets n The variance of a portfolio of the two assets is n n XA 2 + 2 XA XB A, B + XB 2 Notice that a negative covariance leads to some amount of decreased variance of the portfolio (all else constant) n Lower variance lower risk

Lowering risk and getting higher return n In the next lecture, we will see that there are some situations in which we can both increase expected return and lower the standard deviation of a portfolio’s return n See Figure 11. 3 for an example We will derive why this occurs next lecture Look at Figure 11. 4 for a case of eliminating all risk (unrealistic)

An mathematical example of diversification n We will use a two-company world to illustrate that we can find times where diversification is beneficial n n Supertech: A typical company Slowpoke: A “contrarian” company

Supertech and Slowpoke n Supertech n n n Returns closely follow what the market does When times are very good, the stock gets a very high return When times are very bad, the stock loses money n Slowpoke n n n Returns do not coincide with the market as a whole This stock does well in times of recession During normal times, this stock loses money

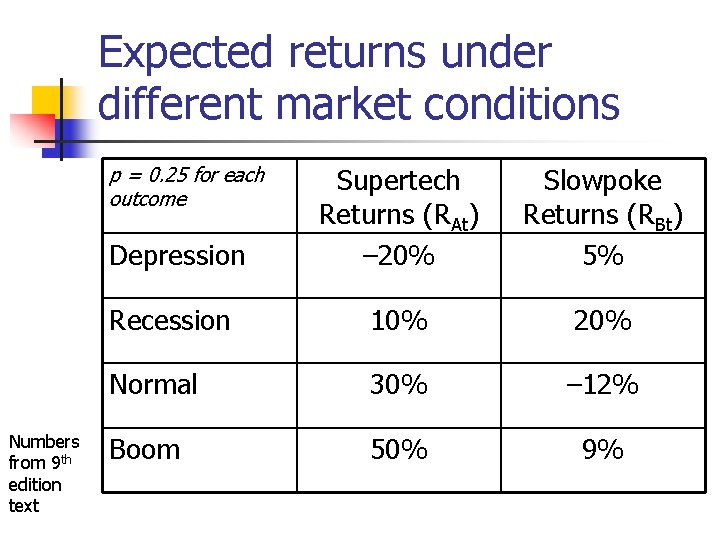
Expected returns under different market conditions p = 0. 25 for each outcome Numbers from 9 th edition text Depression Supertech Returns (RAt) – 20% Slowpoke Returns (RBt) 5% Recession 10% 20% Normal 30% – 12% Boom 50% 9%

Calculating standard deviation of a stock’s returns n There are five steps involved in calculating the standard deviation of the returns of each stock n n n Step 1: Calculate the expected return of the stock Step 2: Find the difference between expected return and actual return for the stock Step 3: Take the square of each number Step 4: Calculate the average squared deviation (this is variance) Step 5: Take the square root of the variance

Step 1: Calculate the expected return of the stock n Supertech n n (– 0. 2 + 0. 1 + 0. 3 + 0. 5) / 4 = 0. 175 = 17. 5% Slowpoke n (0. 05 + 0. 2 – 0. 12 + 0. 09) / 4 = 0. 055 = 5. 5%

Step 2: Difference between expected return and actual return n Supertech n n n Depression: – 0. 2 – 0. 175 = – 0. 375 Recession: 0. 1 – 0. 175 = – 0. 075 Normal: 0. 3 – 0. 175 = 0. 125 Boom: 0. 5 – 0. 175 = 0. 325 Slowpoke n n Depression: 0. 05 – 0. 055 = – 0. 005 Recession: 0. 20 – 0. 055 = 0. 145 Normal: – 0. 12 – 0. 055 = – 0. 175 Boom: 0. 09 – 0. 055 = 0. 035

Step 3: Take the square of each number n Supertech n n n Depression: – 0. 375 0. 140625 Recession: – 0. 075 0. 005625 Normal: 0. 125 0. 015625 Boom: 0. 325 0. 105625 Slowpoke n n Depression: – 0. 005 0. 000025 Recession: 0. 145 0. 021025 Normal: – 0. 175 0. 030625 Boom: 0. 035 0. 001225

Step 4: Calculate the average squared deviation n Supertech n n The average of 0. 140625, 0. 005625, 0. 015625, and 0. 105625 is 0. 066875 Slowpoke n The average of 0. 000025, 0. 021025, 0. 030625, and 0. 001225 is 0. 013225

Step 5: Take the square root of the variance n Supertech n n n sqrt(0. 066875) = 0. 2586 The standard deviation of Supertech’s return is 25. 86% Slowpoke n n sqrt(0. 013225) = 0. 115 The standard deviation of Slowpoke’s return is 11. 5%

Other things to consider n Notice a difference in standard deviation calculation in Chapter 10 vs. Chapter 11 n n In Chapter 10, we divide by the number of data points minus 1 In Chapter 11, we divide by the number of possible outcomes

Other things to consider n We could have a case in which each state of the world occurs with different probabilities n Example: Stock X could have a return of 10% or 5% n n Probability of 10% return is 80% Probability of 5% return is 20%

Stock X: First three steps to find standard deviation n Step 1: Expected return is 0. 1(0. 8) + 0. 05(0. 2) = 0. 09 n n n Notice that we have the weighted average here Step 2: 0. 10 – 0. 09 = 0. 01; 0. 05 – 0. 09 = – 0. 04 Step 3 (square each number): 0. 01 0. 0001; – 0. 04 0. 0016

Standard deviation: Steps 4 and 5 n Just as in Step 1, we have to calculate a weighted average in Step 4 to get variance n n Step 5: Take the square root of the variance to get the standard deviation n n 0. 0001(0. 8) + 0. 0016(0. 2) = 0. 0004 sqrt(0. 0004) = 0. 02 This wraps up part 1 of our mathematical analysis n Covariance, correlation, and portfolio variance will be covered in the next lecture

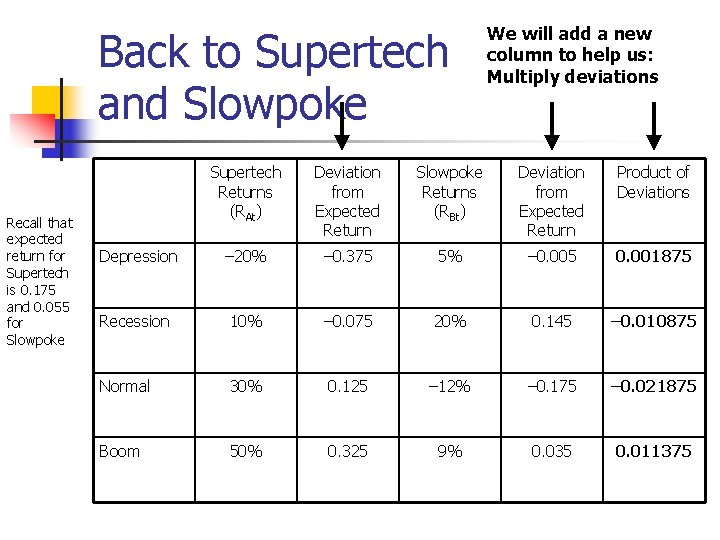
Back to Supertech and Slowpoke Recall that expected return for Supertech is 0. 175 and 0. 055 for Slowpoke We will add a new column to help us: Multiply deviations Supertech Returns (RAt) Deviation from Expected Return Slowpoke Returns (RBt) Deviation from Expected Return Product of Deviations Depression – 20% – 0. 375 5% – 0. 005 0. 001875 Recession 10% – 0. 075 20% 0. 145 – 0. 010875 Normal 30% 0. 125 – 12% – 0. 175 – 0. 021875 Boom 50% 0. 325 9% 0. 035 0. 011375

Finding covariance/correlation n To get covariance, we need to take the average of the numbers in the last column of the previous slide n n n (0. 001875 – 0. 010875 – 0. 021875 + 0. 011375) / 4 – 0. 004875 Correlation (ρ) is the covariance divided by the product of the standard deviation of each stock n n – 0. 004875 / (0. 2585 * 0. 1150) – 0. 1639

Who’s happy in Iceland these days?