CAPITULO III PROGRAMACIN LINEAL Mtodos Cuantitativos I Docente

CAPITULO III PROGRAMACIÒN LINEAL Métodos Cuantitativos I Docente : Ing. Eco. Rodolfo Rojas Gallo

INDICE 3. 1. 3. 2. 3. 3. 3. 4. 3. 5. Concepto Programa Lineal Formulación del programa lineal Ejemplos de formulación de P. L Ejercicios.

3. 1. Concepto La programación lineal es un técnica matemática de planteamiento de problemas de negocios, que emplea el modelo especifico denominado programa lineal. El uso de este modelo facilita la solución de la función objetivo ya que a través del uso de las ecuaciones y gráficos se encuentran primero las variables y luego el resultado final. (Función objetivo)

3. 2. Programa Lineal Modelo matemático que utiliza ecuaciones , inecuaciones , de primer grado para expresar las relaciones entre dos o más variables, y que se encuentran ligadas directamente al objetivo del problema que expresado se conoce como función objetivo de máximo o de mínimo. También el modelo precisa que la variables son mayores o iguales a cero (No negativas)

3. 3. Formulación de un P. L Un programa lineal se plantea del texto del problema, y del cual se extraen la función objetivo ya sea de MAXIMIZACIÒN o de MINIMIZACIÒN, así mismo se establecen las RESTRICCIONES respecto a los recursos o condiciones que nos indiquen en el problema. Por último se indicará que las variables ( X, Y ) son positivas o mayores o iguales a cero

3. 4. Ejemplo de formulaciòn 1. - Una empresa produce dos artículos cuyos precios de venta son 14 y 27 soles respectivamente. La fabricación de ambos pasa por tres procesos con 4000, 3600 y 2900 horas semanales. Para fabricar un artículo A, se requieren 3, 2 y 1 hora en cada proceso. Para el artículo B , se requieren 6, 4 y 2 horas en cada proceso. Se requiere un P. L para MAXIMIZAR el ingreso de la empresa.

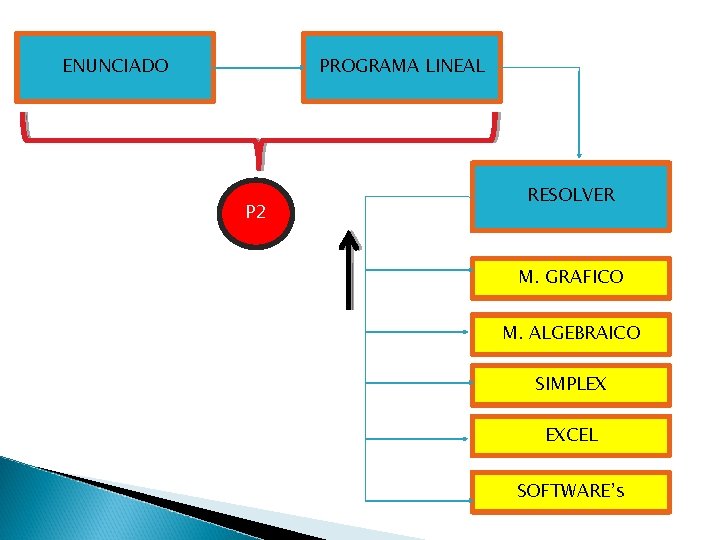
ENUNCIADO PROGRAMA LINEAL P 2 RESOLVER M. GRAFICO M. ALGEBRAICO SIMPLEX EXCEL SOFTWARE’s

FORMULACIÒN Sean : X = Unidades ha producir del artìculo A Y = Unidades ha producir del artìculo B Px = 14, Py = 27 Nos piden MAXIMIZACIÒN de INGRESOS La fabricaciòn pasa por tres procesos con sus respectivos tiempos y disponibilidadesmelaboremos la siguiente tabla AUXILIAR

FORMULACIÒN PROCESO 1 PROCESO 2 PROCESO 3 PRECIOS ARTICULOS A (X) 3 2 1 14 ARIICULOS B (Y) 6 4 2 27 DISPONIBILIDAD 4000 3600 2900

De donde se origino el problema: ◦ Una empresa produce 2 artículos, cuyos precios, son 14 y 27.

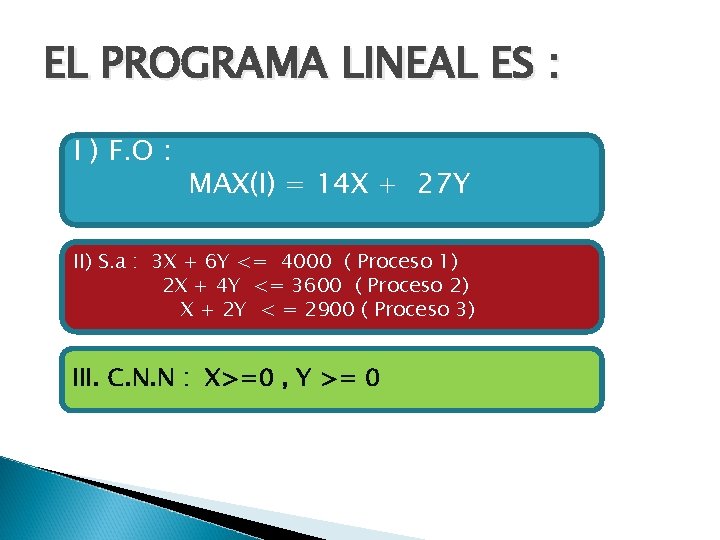
EL PROGRAMA LINEAL ES : I ) F. O : MAX(I) = 14 X + 27 Y II) S. a : 3 X + 6 Y <= 4000 ( Proceso 1) 2 X + 4 Y <= 3600 ( Proceso 2) X + 2 Y < = 2900 ( Proceso 3) III. C. N. N : X>=0 , Y >= 0

3. 5. EJERCICIOS 1. -Un herrero con 80 kgs. de acero y 120 kgs. de aluminio quiere hacer bicicletas de paseo y de montaña que quiere vender, respectivamente a 20. 000 y 15. 000 Bolívares cada una para sacar el máximo beneficio. Para la de paseo empleará 1 kg. De acero y 3 kgs de aluminio, y para la de montaña 2 kgs. de ambos metales. ¿Cuántas bicicletas de paseo y de montaña venderá?

3. 5. EJERCICIOS ◦ Solucion : ◦ Sean : X = cantidad de bicicletas de paseo ha producir ◦ Y = Cantidad de bicicletas de montaña ha producir ◦ Px = 20000 , Py = 15000 ◦ Para el proceso productivo utilizan acero ( 80 Kgs) y aluminio (120 Kgs) ◦ En una tabla podemos resumir el requerimiento unitario para cada tipo de bicicleta según el material

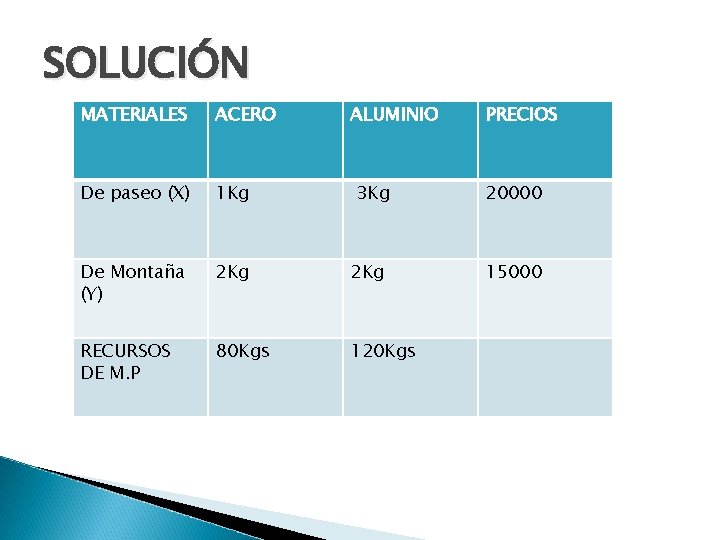
SOLUCIÓN MATERIALES ACERO ALUMINIO De paseo (X) 1 Kg De Montaña (Y) 2 Kg RECURSOS DE M. P 80 Kgs 120 Kgs 3 Kg PRECIOS 20000 15000

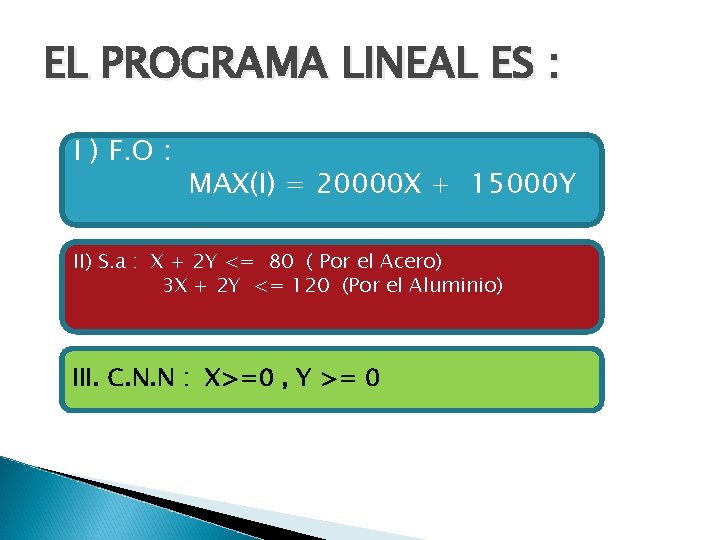
EL PROGRAMA LINEAL ES : I ) F. O : MAX(I) = 20000 X + 15000 Y II) S. a : X + 2 Y <= 80 ( Por el Acero) 3 X + 2 Y <= 120 (Por el Aluminio) III. C. N. N : X>=0 , Y >= 0

3. 5. Ejercicios EJERCICIO 2. -. En un viaje desea transportar al menos 4 Tm. de la mercancía A y un peso de la mercancía B que no sea inferior a la mitad del peso que transporta de A. Sabiendo que cobra 30 pts. /kilo de A y 20 pts. /kilo de B, ¿cómo se debe cargar el camión para obtener la ganancia máxima?

SOLUCIÒN Sean : X = Tns. que transpotarà el camiòn de mercancìa A Y = Tns que trasnportarà el camiòn de l mercancìa B Gx = ganancia por TN de A Gy = Ganancia por TN. De B El camiòn tiene una capacidad màxima de 9 TN Debe transportar por lo menos 4 TN de A Respecto a B , por lo menos debe ser la mitad de A

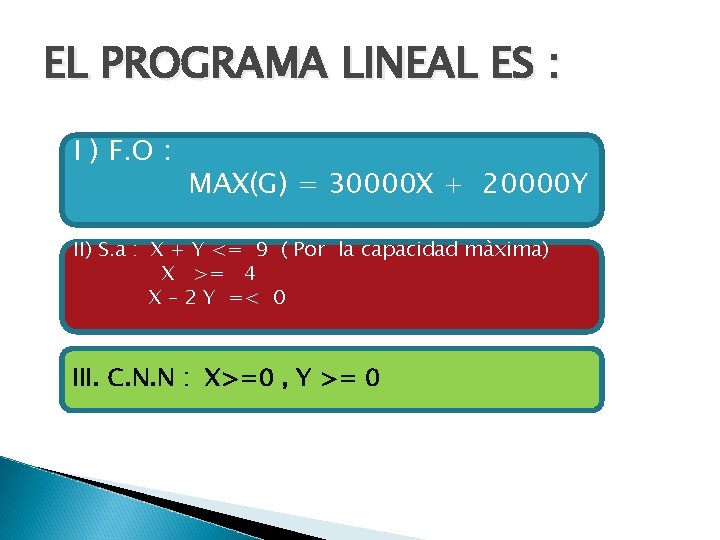
EL PROGRAMA LINEAL ES : I ) F. O : MAX(G) = 30000 X + 20000 Y II) S. a : X + Y <= 9 ( Por la capacidad màxima) X >= 4 X – 2 Y =< 0 III. C. N. N : X>=0 , Y >= 0

3. 5. Ejercicios EJERCICIO 3. -Los 500 alumnos de un colegio van a ir de excursión. La empresa que realiza el viaje dispone de 10 autobuses de 40 plazas y 8 de 50, pero sólo de 11 conductores en ese día. El alquiler de los autobuses pequeños es de 5000 pts. y el de los grandes de 6000 pts. ¿Cuántos autobuses de cada clase convendrá alquilar para que el viaje resulte lo más económico posible?

Ejercicios Sean: X = Cant. de Autobuses de 40, pequeños Y = Cant. de Autobuses de 50, grandes MIN (CT), es el objetivo Px= 5000 Py= 6000 MIN(CT) = 5000 X + 6000 Y La capacidad de los de tipo X, 40 La capacidad de los de tipo Y, 50 La cantidad total de estudiantes es 500

Ejercicios Por lo tanto: 40 X + 50 Y = 500 (Todos los alumnos iran) Se dispone de 11 conductores: X + Y <= 11 Se dispone de 10 buses de tipo X X <= 10 Se dispone de 8 buses de tipo Y Y <= 8

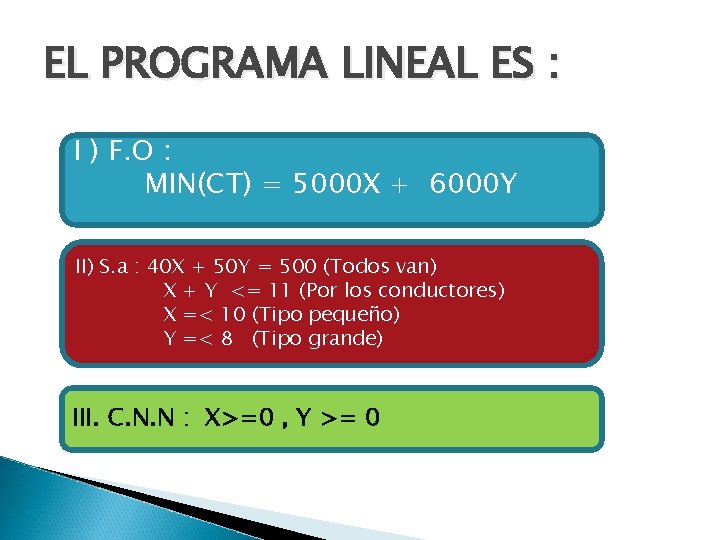
EL PROGRAMA LINEAL ES : I ) F. O : MIN(CT) = 5000 X + 6000 Y II) S. a : 40 X + 50 Y = 500 (Todos van) X + Y <= 11 (Por los conductores) X =< 10 (Tipo pequeño) Y =< 8 (Tipo grande) III. C. N. N : X>=0 , Y >= 0

EJERCICIOS DE PROGRAMACIÓN LINEAL 1. Disponemos de 210. 000 euros para invertir en bolsa. Nos recomiendan dos tipos de acciones. Las del tipo A, que rinden el 10% y las del tipo B, que rinden el 8%. Decidimos invertir un máximo de 130. 000 euros en las del tipo A y como mínimo 60. 000 en las del tipo B. Además queremos que la inversión en las del tipo A sea menor que el doble de la inversión en B. ¿Cuál tiene que ser la distribución de la inversión para obtener el máximo interés anual?

Resolución Sean: X = Dinero invertido en acciones de tipo A Y = Dinero invertido en acciones de tipo B MAX(i); es el objetivo renx = 0. 10 reny = 0. 08 MAX(i) = 0. 10 X + 0. 08 Y Disponemos de 210. 000 euros para invertir en bolsa X + Y = 210000

Resolución Invertimos un máximo de 130. 000 euros en las del tipo A X =< 130000 Invertimos como mínimo 60000 euros en las de tipo B Y => 60000 Queremos que la inversión en las del tipo A sea menor que el doble de la inversión en B X – 2 Y < 0

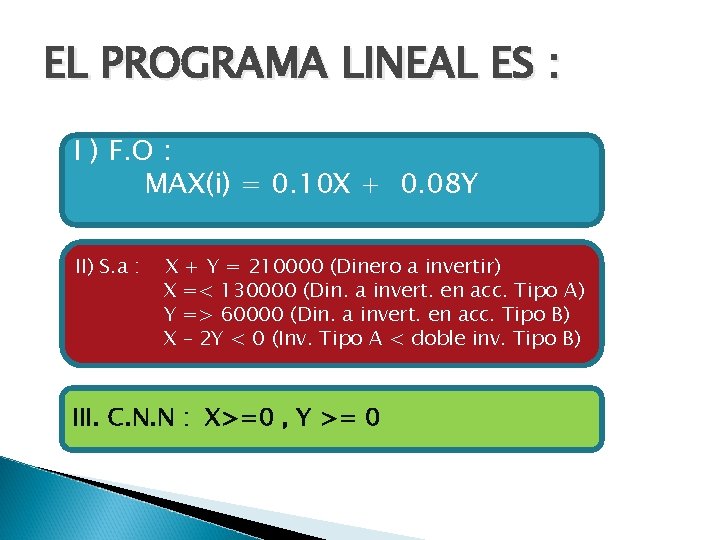
EL PROGRAMA LINEAL ES : I ) F. O : MAX(i) = 0. 10 X + 0. 08 Y II) S. a : X + Y = 210000 (Dinero a invertir) X =< 130000 (Din. a invert. en acc. Tipo A) Y => 60000 (Din. a invert. en acc. Tipo B) X – 2 Y < 0 (Inv. Tipo A < doble inv. Tipo B) III. C. N. N : X>=0 , Y >= 0

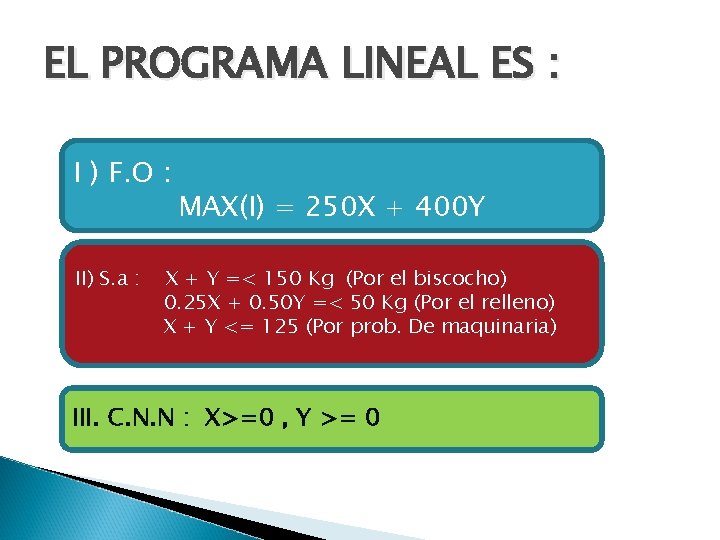
2. En una pastelería se hacen dos tipos de tartas: Vienesa y Real. Cada tarta Vienesa necesita un cuarto de relleno por cada Kg. de bizcocho y produce un beneficio de 250 Pts, mientras que una tarta Real necesita medio Kg. de relleno por cada Kg. de bizcocho y produce 400 Ptas. de beneficio. En la pastelería se pueden hacer diariamente hasta 150 Kg. de bizcocho y 50 Kg. de relleno, aunque por problemas de maquinaria no pueden hacer mas de 125 tartas de cada tipo. ¿Cuántas tartas Vienesas y cuantas Reales deben vender al día para que sea máximo el beneficio?

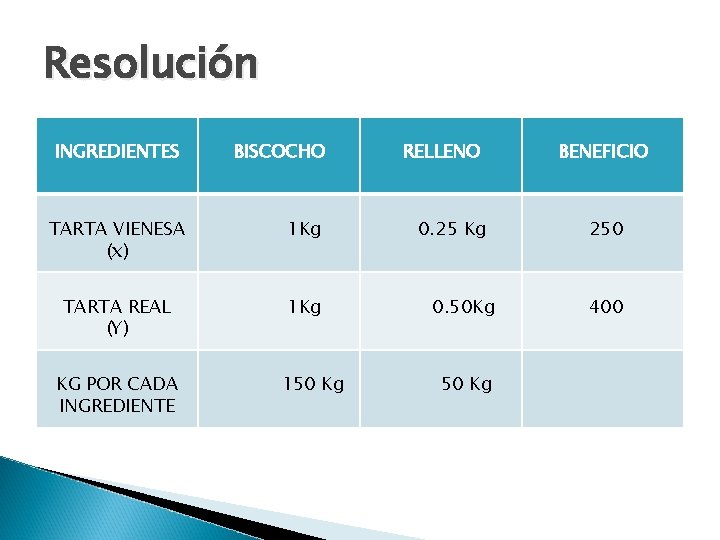
Resolución Sean: X = Número de tartas Vienesa Y = Numero de tartas Real MAX(I); es el objetivo Benx = 250 Ptas. Beny = 400 Ptas. MAX(I) = 250 X + 400 Y En una tabla podemos resumir el requerimiento unitario para cada tipo de tarta:

Resolución INGREDIENTES BISCOCHO TARTA VIENESA (x) 1 Kg TARTA REAL (Y) 1 Kg KG POR CADA INGREDIENTE 150 Kg RELLENO 0. 25 Kg 0. 50 Kg 50 Kg BENEFICIO 250 400

Resolución Por problemas de maquinaria no pueden hacer mas de 125 tartas de cada tipo X <= 125

EL PROGRAMA LINEAL ES : I ) F. O : II) S. a : MAX(I) = 250 X + 400 Y X + Y =< 150 Kg (Por el biscocho) 0. 25 X + 0. 50 Y =< 50 Kg (Por el relleno) X + Y <= 125 (Por prob. De maquinaria) III. C. N. N : X>=0 , Y >= 0

3. Una escuela prepara una excursión para 400 alumnos. La empresa de transporte tiene 8 autocares de 40 plazas y 10 autocares de 50 plazas, pero solo dispone de 9 conductores. El alquiler de un autocar grande cuesta 80 euros y el de uno pequeño, 60 euros. Calcular cuántos de cada tipo hay que utilizar para que la excursión resulte lo mas económica posible para la escuela.

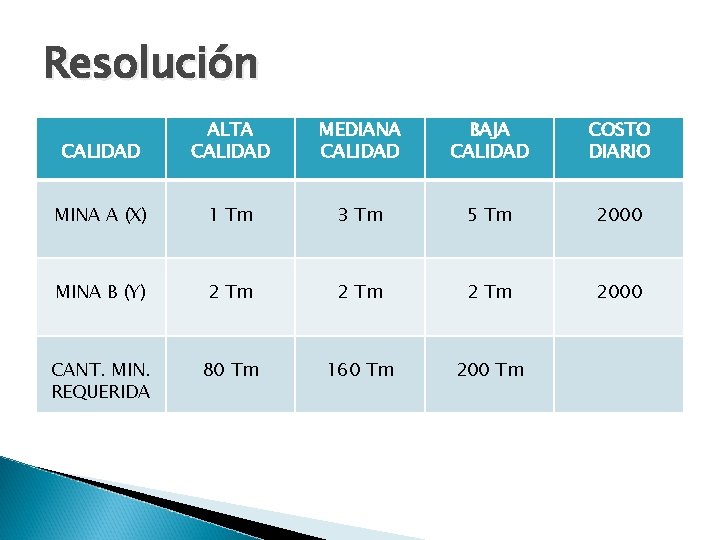
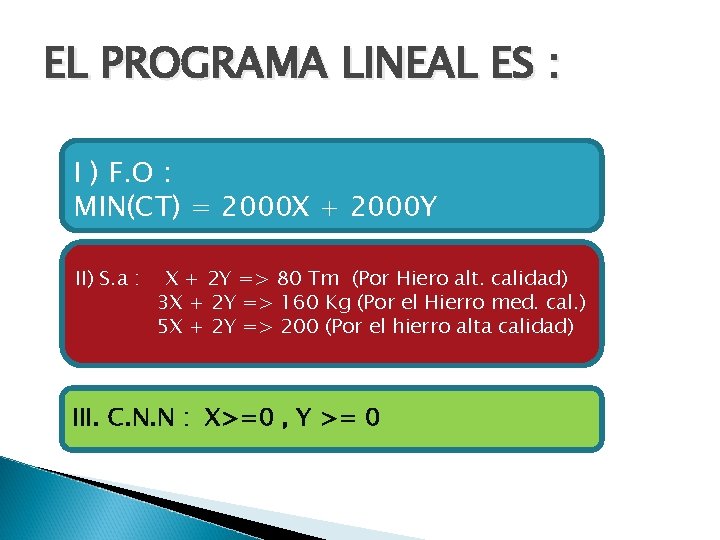
4. -Una compañía posee dos minas: la mina A produce cada día 1 tonelada de hierro de alta calidad, 3 toneladas de calidad media y 5 de baja calidad. La mina B produce cada día 2 toneladas de cada una de las tres calidades. La compañía necesita al menos 80 toneladas de mineral de alta calidad, 160 toneladas de calidad media y 200 de baja calidad. Sabiendo que el coste diario de la operación es de 2000 euros en cada mina ¿cuántos días debe trabajar cada mina para que el coste sea mínimo? .

Resolución Sean: X = Días trabajados en mina A Y = Días trabajados en mina B MIN(CT); es el objetivo Cosx = 2000 euros Cosy = 2000 euros MIN(CT) = 2000 X + 2000 Y Resumimos en una tabla las toneladas de hierro de diferentes calidades producidas en cada mina:

Resolución CALIDAD ALTA CALIDAD MEDIANA CALIDAD BAJA CALIDAD COSTO DIARIO MINA A (X) 1 Tm 3 Tm 5 Tm 2000 MINA B (Y) 2 Tm 2000 CANT. MIN. REQUERIDA 80 Tm 160 Tm 200 Tm

EL PROGRAMA LINEAL ES : I ) F. O : MIN(CT) = 2000 X + 2000 Y II) S. a : X + 2 Y => 80 Tm (Por Hiero alt. calidad) 3 X + 2 Y => 160 Kg (Por el Hierro med. cal. ) 5 X + 2 Y => 200 (Por el hierro alta calidad) III. C. N. N : X>=0 , Y >= 0

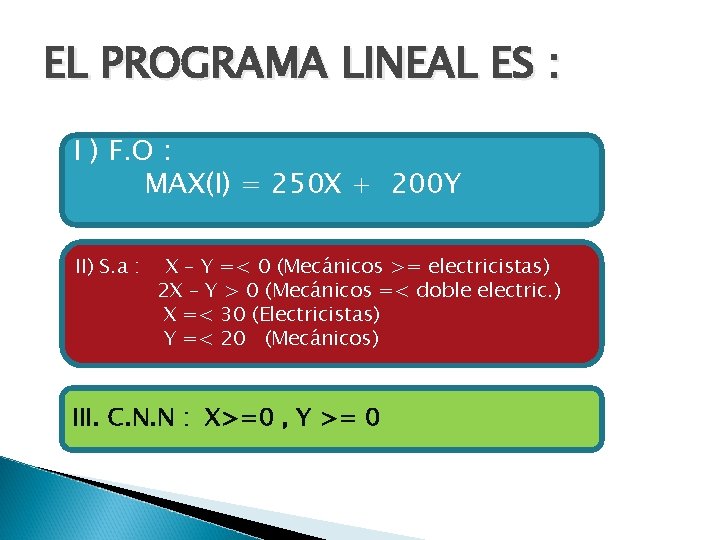
5. Se va a organizar una planta de un taller de automóviles donde van a trabajar electricistas y mecánicos. Por necesidades de mercado, es necesario que haya mayor o igual número de mecánicos que de electricistas y que el número de mecánicos no supere al doble que el de electricistas. En total hay disponibles 30 electricistas y 20 mecánicos. El beneficio de la empresa por jornada es de 250 euros por electricista y 200 euros por mecánico. ¿Cuántos trabajadores de cada clase deben elegirse para obtener el máximo beneficio y cual es este?

Resolución Sean: X = Numero de electricistas Y = Numero de mecánicos MAX(I); es el objetivo Benx = 250 euros Beny = 200 euros MAX(I) = 250 X + 200 Y Es necesario que haya mayor o igual número de mecánicos que de electricistas X – Y =< 0

Resolución El número de mecánicos no supera al doble que el de electricistas 2 X – Y => 0 Hay disponibles 30 electricistas X =< 30 Hay disponibles 20 mecánicos Y =< 20

EL PROGRAMA LINEAL ES : I ) F. O : MAX(I) = 250 X + 200 Y II) S. a : X – Y =< 0 (Mecánicos >= electricistas) 2 X – Y > 0 (Mecánicos =< doble electric. ) X =< 30 (Electricistas) Y =< 20 (Mecánicos) III. C. N. N : X>=0 , Y >= 0

6. Para recorrer un determinado trayecto, una compañía aérea desea ofertar, a lo sumo, 5000 plazas de dos tipos: T(turista) y P(primera). La ganancia correspondiente a cada plaza de tipo T es de 30 euros, mientras que la ganancia del tipo P es de 40 euros. El número de plazas tipo T no puede exceder de 4500 y el del tipo P, debe ser, como máximo, la tercera parte de las del tipo T que se oferten. Calcular cuántas tienen que ofertarse de cada clase para que las ganancias sean máximas.

Resolución Sean: X = Numero de plazas T (Turista) Y = Numero de plazas P (Primera) MAX(I); es el objetivo Ganx = 30 euros Gany = 40 euros MAX(I) = 30 X + 40 Y Hay 5000 plazas, a lo sumo, para los dos tipos: X + Y =< 5000

Resolución Número de plazas tipo T: X =< 4500 Número de plazas tipo P: Debe ser, como máximo, la tercera parte de las del tipo T X – 3 Y =>0

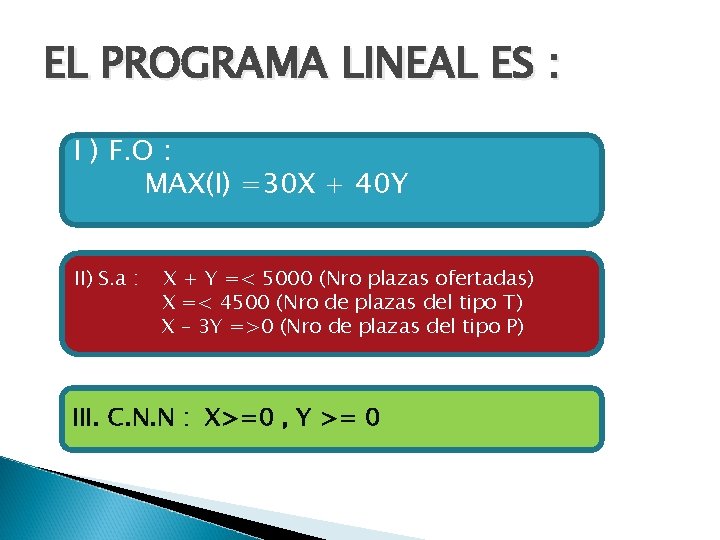
EL PROGRAMA LINEAL ES : I ) F. O : MAX(I) =30 X + 40 Y II) S. a : X + Y =< 5000 (Nro plazas ofertadas) X =< 4500 (Nro de plazas del tipo T) X – 3 Y =>0 (Nro de plazas del tipo P) III. C. N. N : X>=0 , Y >= 0