Capacitors and Inductors Vishal Jethva svbitec wordpress com

Capacitors and Inductors Vishal Jethva svbitec. wordpress. com 1

Chap. 6, Capacitors and Inductors • • • Introduction Capacitors Series and Parallel Capacitors Inductors Series and Parallel Inductors svbitec. wordpress. com 2

6. 1 Introduction • • Resistor: a passive element which dissipates energy only Two important passive linear circuit elements: 1) Capacitor 2) Inductor • Capacitor and inductor can store energy only and they can neither generate nor dissipate energy. svbitec. wordpress. com 3

Michael Faraday (1971 -1867) svbitec. wordpress. com 4

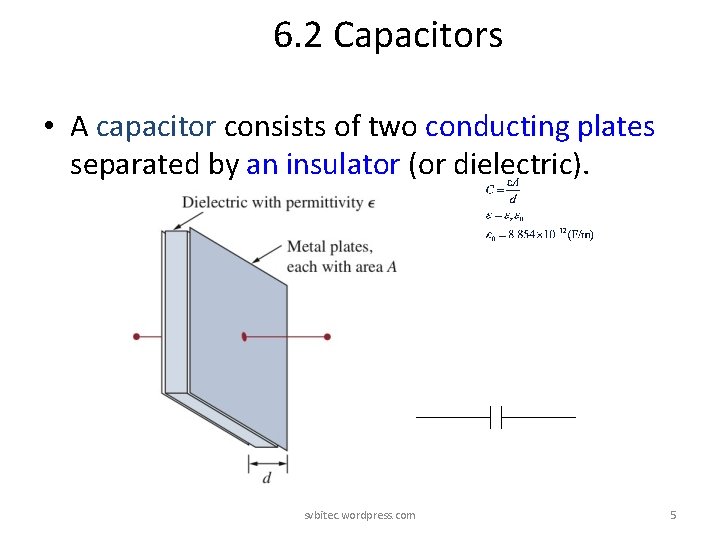
6. 2 Capacitors • A capacitor consists of two conducting plates separated by an insulator (or dielectric). svbitec. wordpress. com 5

• Three factors affecting the value of capacitance: 1. Area: the larger the area, the greater the capacitance. 2. Spacing between the plates: the smaller the spacing, the greater the capacitance. 3. Material permittivity: the higher the permittivity, the greater the capacitance. svbitec. wordpress. com 6

Fig 6. 4 (a) Polyester capacitor, (b) Ceramic capacitor, (c) Electrolytic capacitor svbitec. wordpress. com 7

Fig 6. 5 Variable capacitors svbitec. wordpress. com 8

Fig 6. 3 svbitec. wordpress. com 9

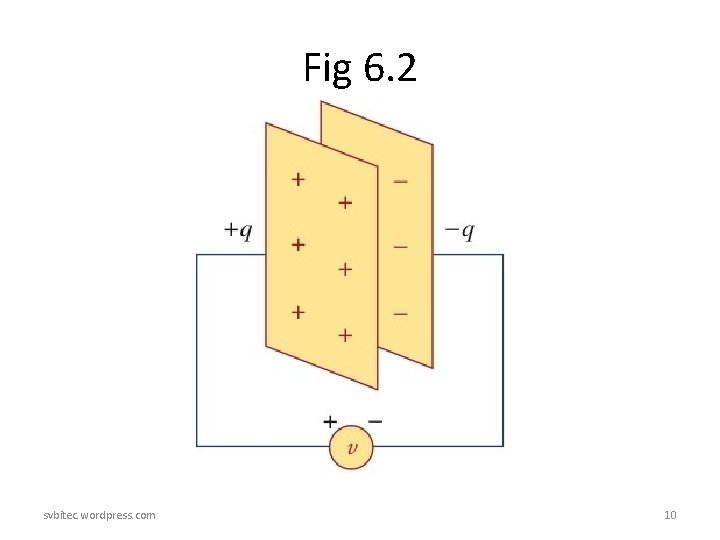
Fig 6. 2 svbitec. wordpress. com 10

Charge in Capacitors • The relation between the charge in plates and the voltage across a capacitor is given below. q Linear Nonlinear v svbitec. wordpress. com 11

Voltage Limit on a Capacitor • Since q=Cv, the plate charge increases as the voltage increases. The electric field intensity between two plates increases. If the voltage across the capacitor is so large that the field intensity is large enough to break down the insulation of the dielectric, the capacitor is out of work. Hence, every practical capacitor has a maximum limit on its operating voltage. svbitec. wordpress. com 12

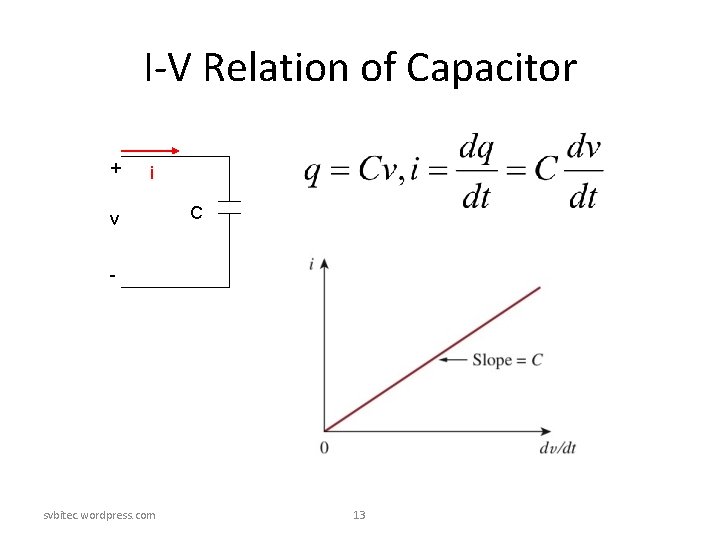
I-V Relation of Capacitor + i v C - svbitec. wordpress. com 13

Physical Meaning + v i C - • when v is a constant voltage, then i=0; a constant voltage across a capacitor creates no current through the capacitor, the capacitor in this case is the same as an open circuit. • If v is abruptly changed, then the current will have an infinite value that is practically impossible. Hence, a capacitor is impossible to have an abrupt change in its voltage except an infinite current is applied. svbitec. wordpress. com 14

Fig 6. 7 • A capacitor is an open circuit to dc. • The voltage on a capacitor cannot change abruptly. Abrupt change svbitec. wordpress. com 15

+ v i C - • The charge on a capacitor is an integration of current through the capacitor. Hence, the memory effect counts. svbitec. wordpress. com 16

Energy Storing in Capacitor + v i C - svbitec. wordpress. com 17

Model of Practical Capacitor svbitec. wordpress. com 18

Example 6. 1 (a) Calculate the charge stored on a 3 -p. F capacitor with 20 V across it. (b) Find the energy stored in the capacitor. svbitec. wordpress. com 19

Example 6. 1 Solution: (a) Since (b) The energy stored is svbitec. wordpress. com 20

Example 6. 2 • The voltage across a 5 - F capacitor is Calculate the current through it. Solution: • By definition, the current is svbitec. wordpress. com 21

Example 6. 3 • Determine the voltage across a 2 - F capacitor if the current through it is Assume that the initial capacitor voltage is zero. Solution: • Since svbitec. wordpress. com 22

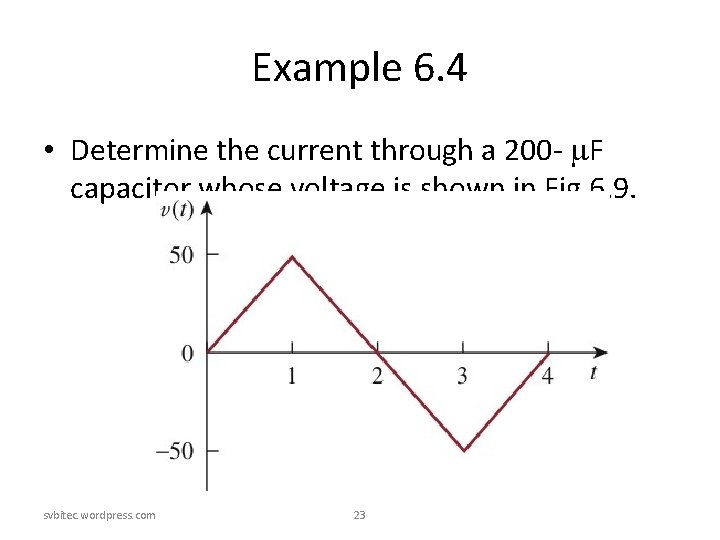
Example 6. 4 • Determine the current through a 200 - F capacitor whose voltage is shown in Fig 6. 9. svbitec. wordpress. com 23

Example 6. 4 Solution: • The voltage waveform can be described mathematically as svbitec. wordpress. com 24

Example 6. 4 • Since i = C dv/dt and C = 200 F, we take the derivative of to obtain • Thus the current waveform is shown in Fig. 6. 10. svbitec. wordpress. com 25

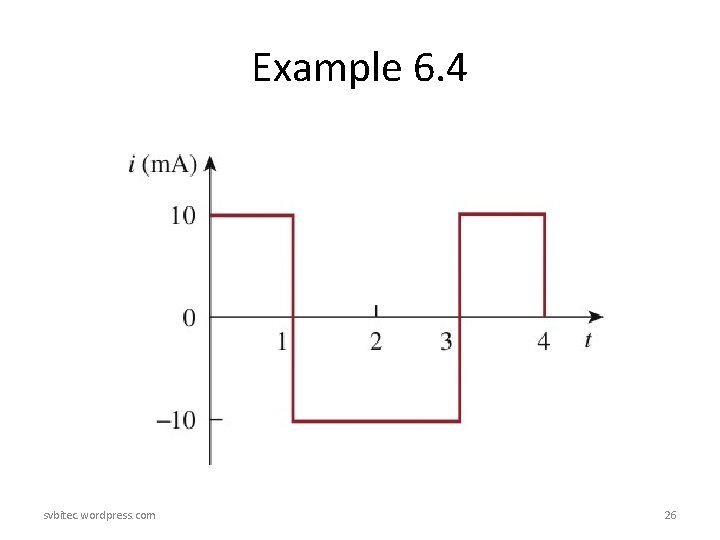
Example 6. 4 svbitec. wordpress. com 26

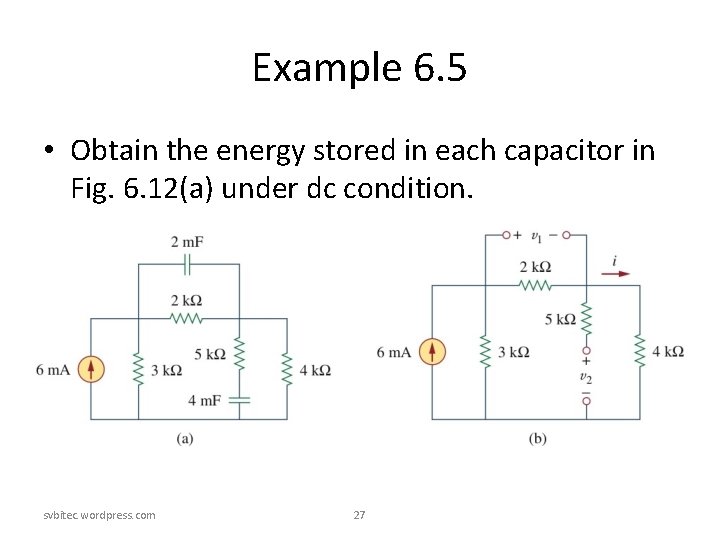
Example 6. 5 • Obtain the energy stored in each capacitor in Fig. 6. 12(a) under dc condition. svbitec. wordpress. com 27

Example 6. 5 Solution: • Under dc condition, we replace each capacitor with an open circuit. By current division, svbitec. wordpress. com 28

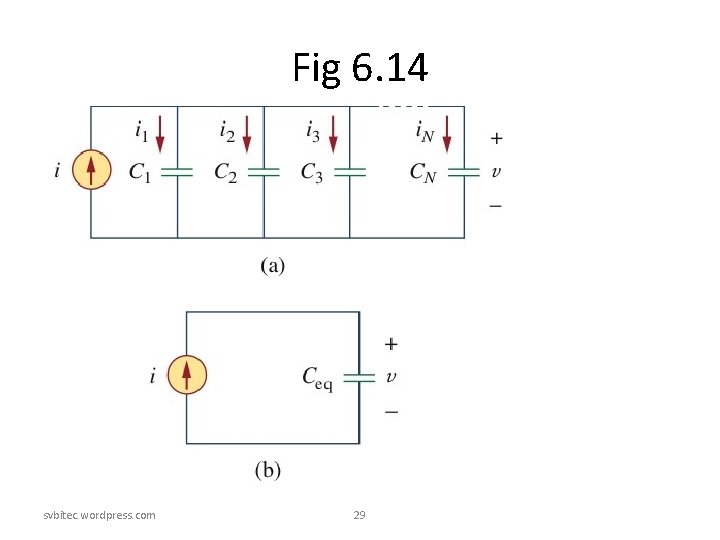
Fig 6. 14 svbitec. wordpress. com 29

6. 3 Series and Parallel Capacitors • The equivalent capacitance of N parallelconnected capacitors is the sum of the individual capacitance. svbitec. wordpress. com 30

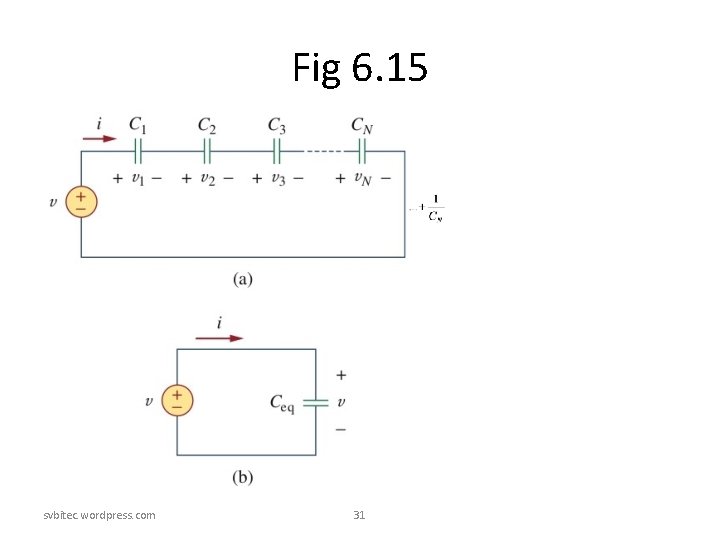
Fig 6. 15 svbitec. wordpress. com 31

Series Capacitors • The equivalent capacitance of series-connected capacitors is the reciprocal of the sum of the reciprocals of the individual capacitances. svbitec. wordpress. com 32

Summary • These results enable us to look the capacitor in this way: 1/C has the equivalent effect as the resistance. The equivalent capacitor of capacitors connected in parallel or series can be obtained via this point of view, so is the Y△ connection and its transformation svbitec. wordpress. com 33

Example 6. 6 • Find the equivalent capacitance seen between terminals a and b of the circuit in Fig 6. 16. svbitec. wordpress. com 34

Example 6. 6 Solution: svbitec. wordpress. com 35

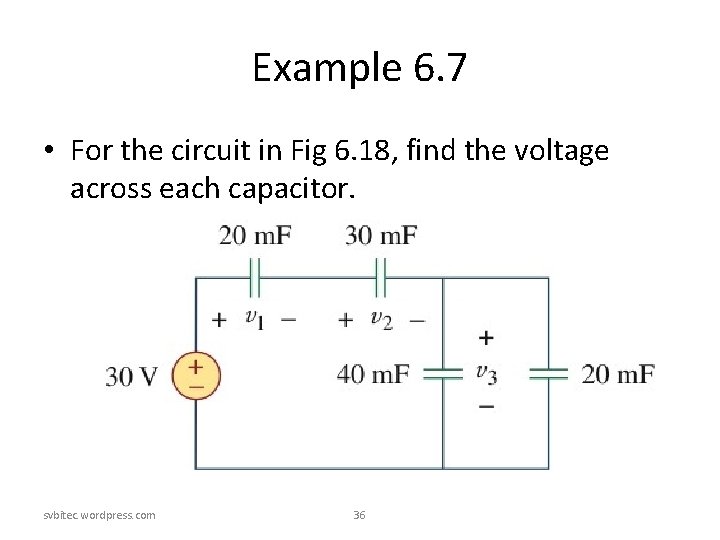
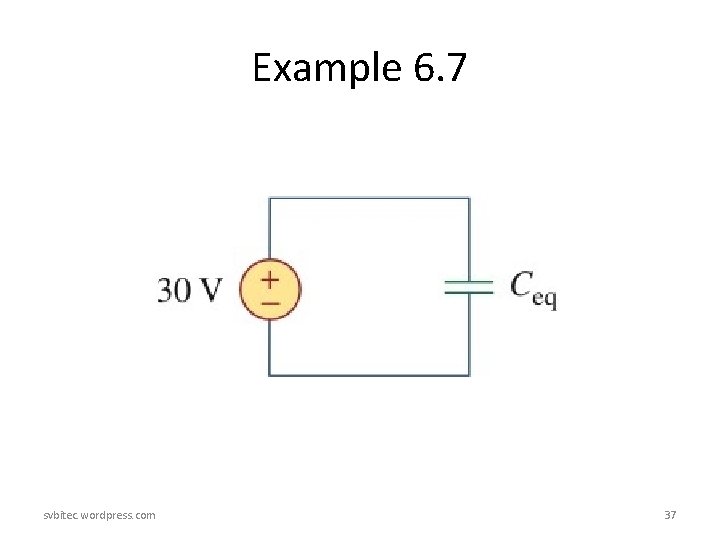
Example 6. 7 • For the circuit in Fig 6. 18, find the voltage across each capacitor. svbitec. wordpress. com 36

Example 6. 7 svbitec. wordpress. com 37

Example 6. 7 Solution: • Two parallel capacitors: • Total charge • This is the charge on the 20 -m. F and 30 -m. F capacitors, because they are in series with the 30 v source. ( A crude way to see this is to imagine that charge acts like current, since i = dq/dt) svbitec. wordpress. com 38

• Therefore, Example 6. 7 • Having determined v 1 and v 2, we now use KVL to determine v 3 by • Alternatively, since the 40 -m. F and 20 -m. F capacitors are in parallel, they have the same voltage v 3 and their combined capacitance is 40+20=60 m. F. svbitec. wordpress. com 39

Joseph Henry (1979 -1878) svbitec. wordpress. com 40

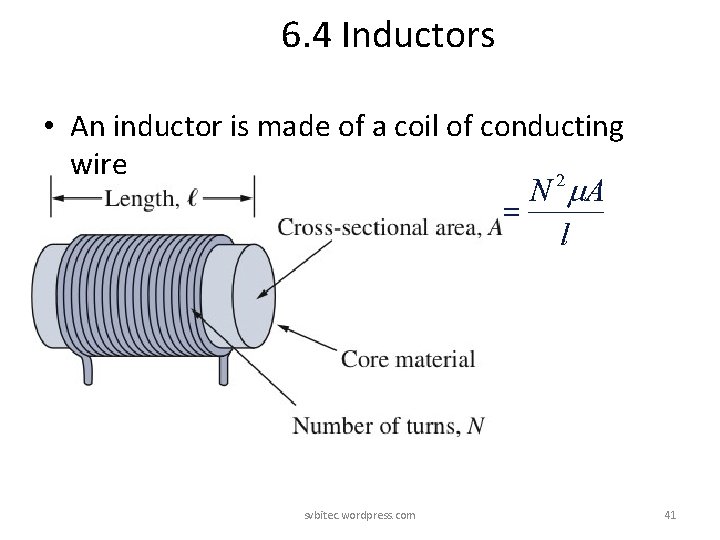
6. 4 Inductors • An inductor is made of a coil of conducting wire svbitec. wordpress. com 41

Fig 6. 22 svbitec. wordpress. com 42

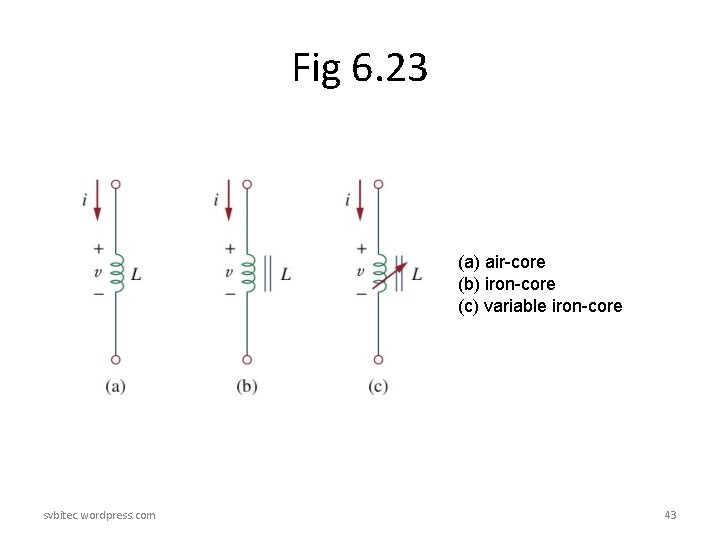
Fig 6. 23 (a) air-core (b) iron-core (c) variable iron-core svbitec. wordpress. com 43

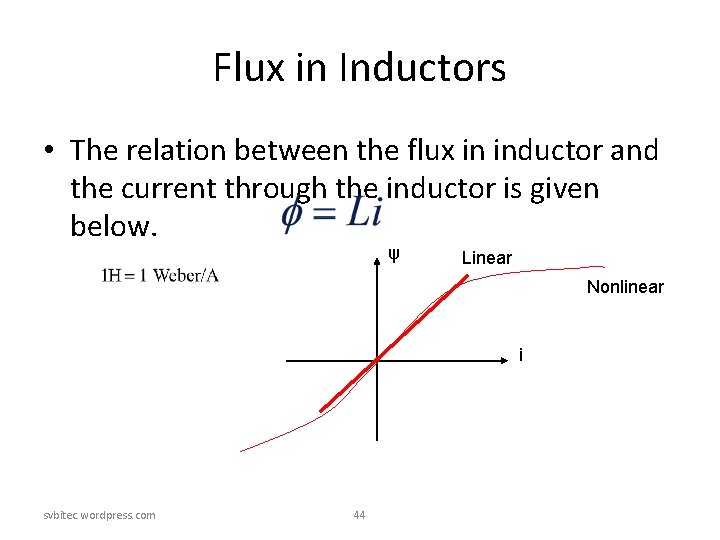
Flux in Inductors • The relation between the flux in inductor and the current through the inductor is given below. ψ Linear Nonlinear i svbitec. wordpress. com 44

Energy Storage Form • An inductor is a passive element designed to store energy in the magnetic field while a capacitor stores energy in the electric field. svbitec. wordpress. com 45

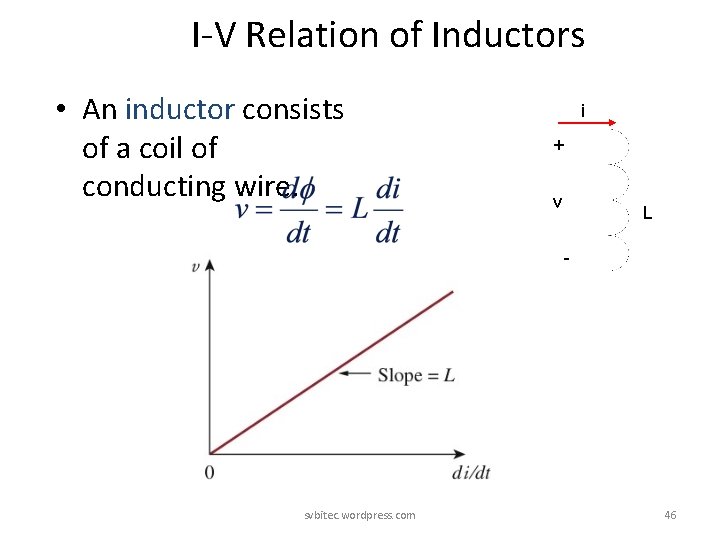
I-V Relation of Inductors • An inductor consists of a coil of conducting wire. i + v L - svbitec. wordpress. com 46

Physical Meaning • When the current through an inductor is a constant, then the voltage across the inductor is zero, same as a short circuit. • No abrupt change of the current through an inductor is possible except an infinite voltage across the inductor is applied. • The inductor can be used to generate a high voltage, for example, used as an igniting element. svbitec. wordpress. com 47

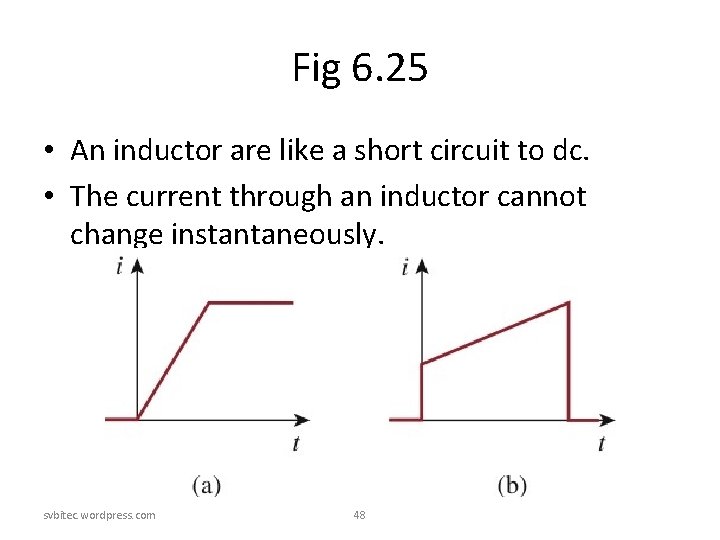
Fig 6. 25 • An inductor are like a short circuit to dc. • The current through an inductor cannot change instantaneously. svbitec. wordpress. com 48

+ v L - svbitec. wordpress. com 49

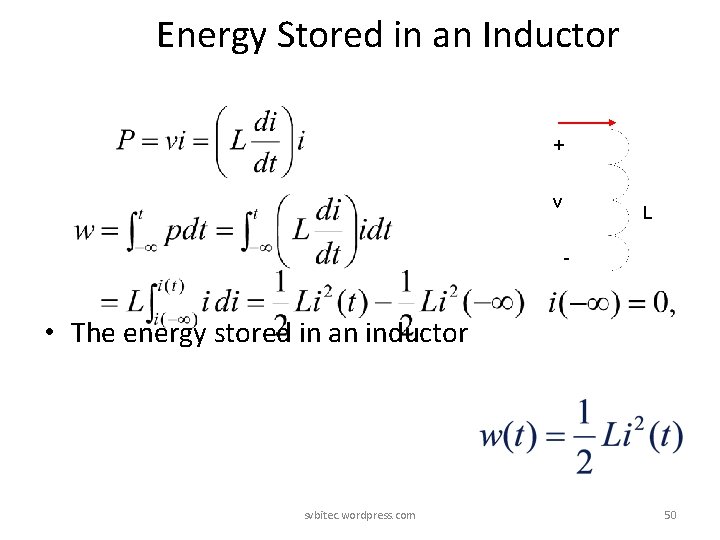
Energy Stored in an Inductor + v L - • The energy stored in an inductor svbitec. wordpress. com 50

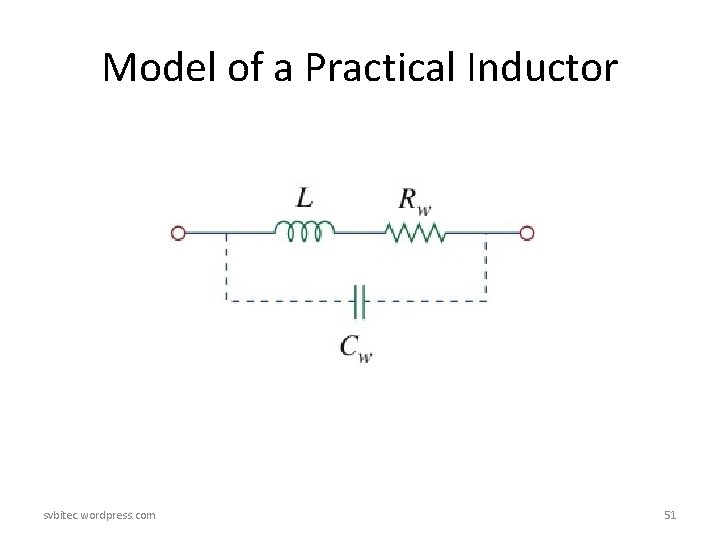
Model of a Practical Inductor svbitec. wordpress. com 51

Example 6. 8 • The current through a 0. 1 -H inductor is i(t) = 10 te-5 t A. Find the voltage across the inductor and the energy stored in it. Solution: svbitec. wordpress. com 52

Example 6. 9 • Find the current through a 5 -H inductor if the voltage across it is Also find the energy stored within 0 < t < 5 s. Assume i(0)=0. Solution: svbitec. wordpress. com 53

Example 6. 9 svbitec. wordpress. com 54

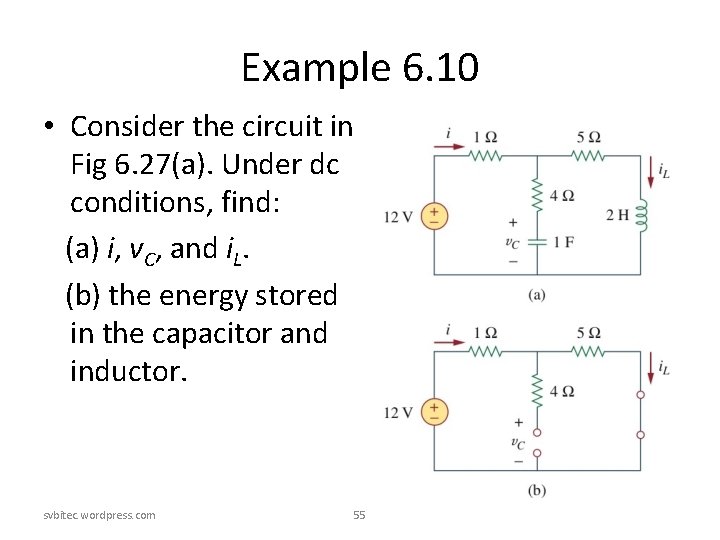
Example 6. 10 • Consider the circuit in Fig 6. 27(a). Under dc conditions, find: (a) i, v. C, and i. L. (b) the energy stored in the capacitor and inductor. svbitec. wordpress. com 55

Example 6. 10 Solution: svbitec. wordpress. com 56

Inductors in Series svbitec. wordpress. com 57

Inductors in Parallel svbitec. wordpress. com 58

6. 5 Series and Parallel Inductors • Applying KVL to the loop, • Substituting vk = Lk di/dt results in svbitec. wordpress. com 59

Parallel Inductors • Using KCL, • But svbitec. wordpress. com 60

• The inductor in various connection has the same effect as the resistor. Hence, the Y-Δ transformation of inductors can be similarly derived. svbitec. wordpress. com 61

Table 6. 1 svbitec. wordpress. com 62

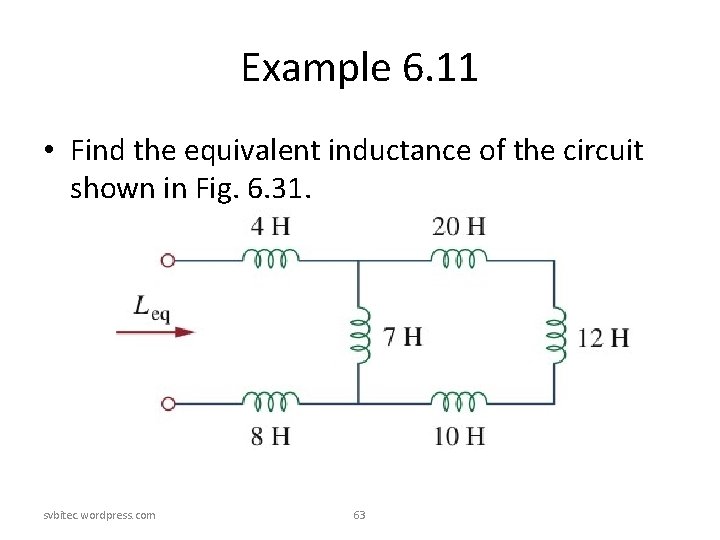
Example 6. 11 • Find the equivalent inductance of the circuit shown in Fig. 6. 31. svbitec. wordpress. com 63

Example 6. 11 • Solution: svbitec. wordpress. com 64

Practice Problem 6. 11 svbitec. wordpress. com 65

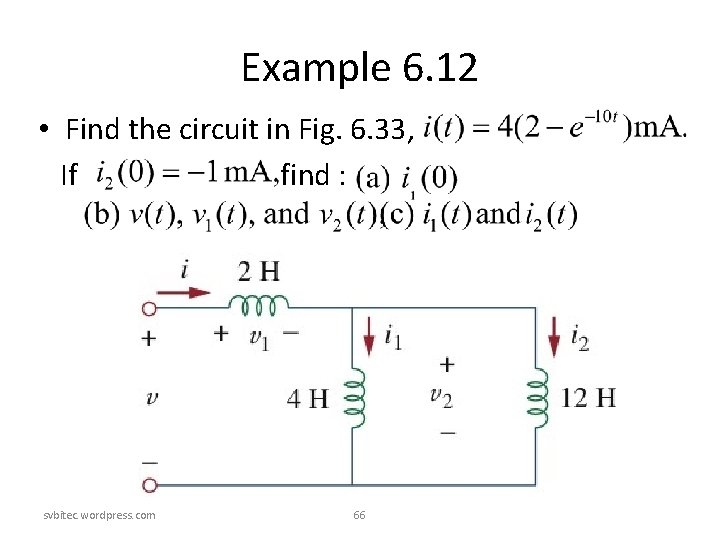
Example 6. 12 • Find the circuit in Fig. 6. 33, If find : svbitec. wordpress. com 66

Example 6. 12 Solution: svbitec. wordpress. com 67

Example 6. 12 svbitec. wordpress. com 68