Capacitors and Capacitance Capacitors are devices that can

Capacitors and Capacitance Capacitors are devices that can store a charge Q at some voltage V. The greater the capacitance, the more charge that can be stored. The equation for capacitance, C, is very simple: Even an isolated conducting sphere has capacitance. We just take the equation for the electric potential of a point charge (which also applies to conducting spheres, and find the above ratio: Q R Michael Faraday

Find the capacitance of “Old Sparky” A capacitance of ~ 20 p. F is not very big. If this Van de Graaf generator could reach 1, 000 V, the total charge on the dome would be only 20 m. C. This is one reason this device is safe. The other is that high voltage causes charge to travel along the surface of objects (such as our bodies).

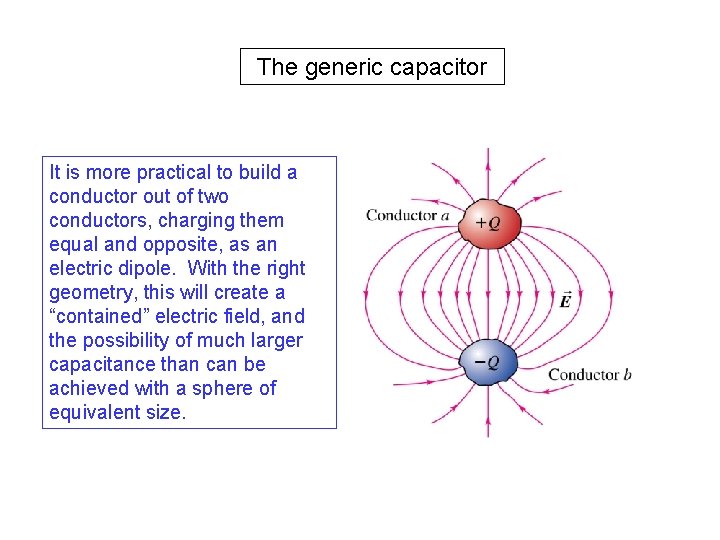
The generic capacitor It is more practical to build a conductor out of two conductors, charging them equal and opposite, as an electric dipole. With the right geometry, this will create a “contained” electric field, and the possibility of much larger capacitance than can be achieved with a sphere of equivalent size.

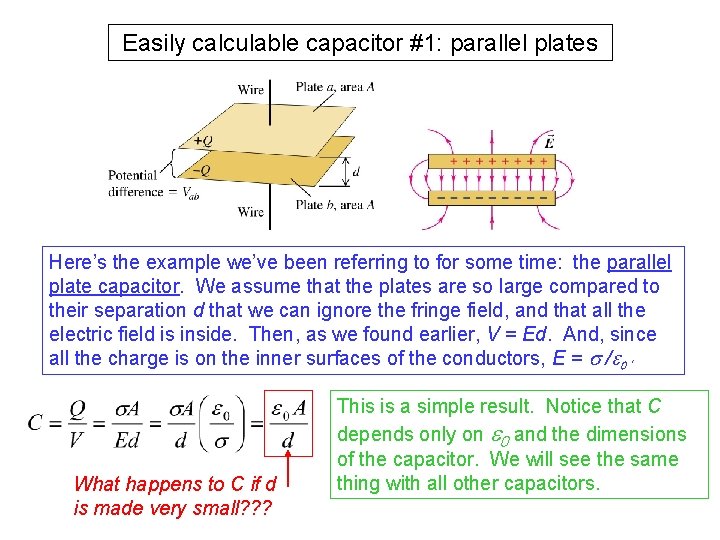
Easily calculable capacitor #1: parallel plates Here’s the example we’ve been referring to for some time: the parallel plate capacitor. We assume that the plates are so large compared to their separation d that we can ignore the fringe field, and that all the electric field is inside. Then, as we found earlier, V = Ed. And, since all the charge is on the inner surfaces of the conductors, E = s /e 0 ‘ What happens to C if d is made very small? ? ? This is a simple result. Notice that C depends only on e 0 and the dimensions of the capacitor. We will see the same thing with all other capacitors.

Calculable capacitor #2: concentric spheres This calculation is also easy. We use the equation for the electric potential of a sphere of a given radius and charge. We apply it once to the inner sphere, and again to the outer, to find the voltage difference between the two. (By Gauss’s Law, the only electric field is between the two spheres. ) Then, the capacitance of a spherical capacitor (in vacuum) is:

Calculable capacitor #3: coaxial infinite cylinders We’ve done most of the work already for this, by finding the difference in electric potential at two different radii in a cylindrically symmetric geometry. We simply use that earlier result for DV, and find C from the basic equation. Notice that to calculate a Q for the capacitance equation, we need to choose a length, L, so that Q = l. L: Capacitance per unit length (in vacuum).

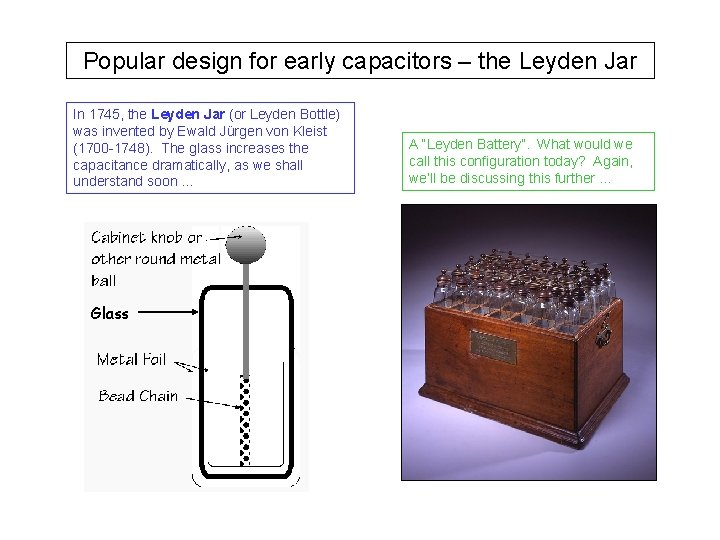
Popular design for early capacitors – the Leyden Jar In 1745, the Leyden Jar (or Leyden Bottle) was invented by Ewald Jürgen von Kleist (1700 -1748). The glass increases the capacitance dramatically, as we shall understand soon … Glass A “Leyden Battery”. What would we call this configuration today? Again, we’ll be discussing this further …

Early charging machines Induction machine invented by James Wimshurst c. 1880. The two disks, with narrow tin-foil strips glued around the rim, are rotated in opposite directions by a system of pulleys and belts. At each side there is a conductor, terminating in metal brushes that rub against the tin-foil sectors. The charge is induced in two jaw collectors and stored in a pair of Leyden jars connected to two sliding electrodes. This machine was highly popular and is still used today for teaching purposes. It worked well even in damp weather and did not reverse polarity. Apart from laboratory demonstrations, it was used for medical treatment and as a high-voltage source for the first X-ray tubes.

By ~ 1905. Large machines!

Modern capacitors: many sizes, shapes, and types http: //en. wikipedia. org/wiki/Capacitor http: //www. sparkmuseum. com/RADIOS. HTM http: //www. uoguelph. ca/~antoon/gadgets/caps. html Capacitor types: (most common types are in red). Metal film: Made from polymer foil with a layer of metal deposited on surface. They have good quality and stability, and are suitable for timer circuits and high frequencies. Mica: Similar to metal film. Often high voltage. Suitable for high frequencies. Paper: Used for high voltages. Glass: Used for high voltages. Stable temperature coefficient in a wide range of temperatures. Ceramic: Chips of altering layers of metal and ceramic. Very common, they find use in low-precision coupling and filtering applications. Good for high frequencies. Electrolytic: Polarized. Similar to metal film in construction, but the electrodes are made of aluminum etched for much higher surface area, and the dielectric is soaked with liquid electrolyte. Can achieve high capacities. Tantalum: Like electrolytic. Polarized. Better performance at higher frequencies. Can tolerate low temperatures. Supercapacitors: Made from carbon aerogel, carbon nanotubes, or highly porous electrode materials. Extremely high capacity. More discussion to come on the subject of dielectrics…

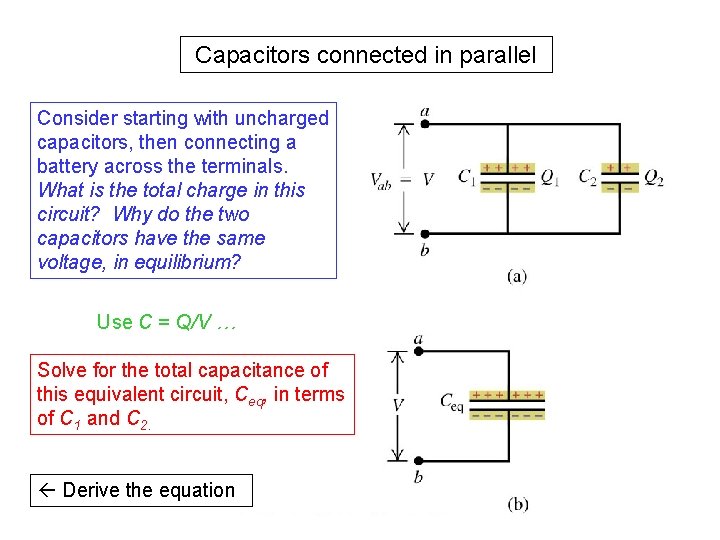
Capacitors connected in parallel Consider starting with uncharged capacitors, then connecting a battery across the terminals. What is the total charge in this circuit? Why do the two capacitors have the same voltage, in equilibrium? Use C = Q/V … Solve for the total capacitance of this equivalent circuit, Ceq, in terms of C 1 and C 2. Derive the equation

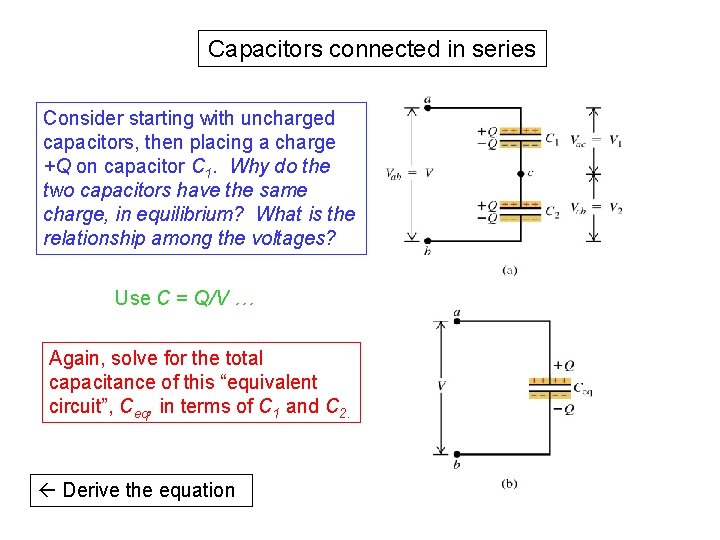
Capacitors connected in series Consider starting with uncharged capacitors, then placing a charge +Q on capacitor C 1. Why do the two capacitors have the same charge, in equilibrium? What is the relationship among the voltages? Use C = Q/V … Again, solve for the total capacitance of this “equivalent circuit”, Ceq, in terms of C 1 and C 2. Derive the equation

Equations for capacitors connected in parallel and in series Parallel: Series:

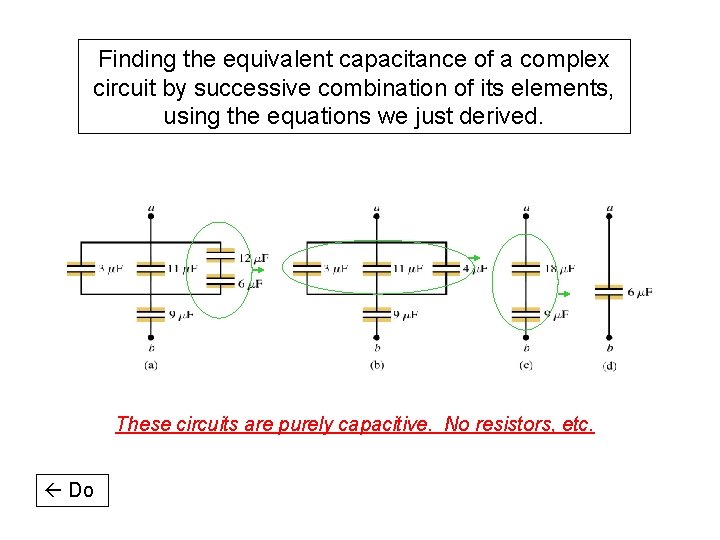
Finding the equivalent capacitance of a complex circuit by successive combination of its elements, using the equations we just derived. These circuits are purely capacitive. No resistors, etc. Do

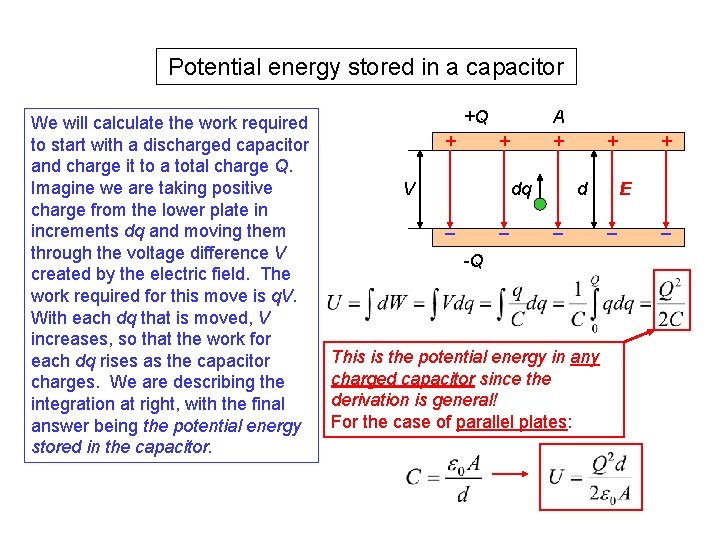
Potential energy stored in a capacitor We will calculate the work required to start with a discharged capacitor and charge it to a total charge Q. Imagine we are taking positive charge from the lower plate in increments dq and moving them through the voltage difference V created by the electric field. The work required for this move is q. V. With each dq that is moved, V increases, so that the work for each dq rises as the capacitor charges. We are describing the integration at right, with the final answer being the potential energy stored in the capacitor. +Q + A + + V dq _ _ + d _ -Q This is the potential energy in any charged capacitor since the derivation is general! For the case of parallel plates: + E _ _

General expressions for potential energy in a capacitor, and energy density of the electric field. There are two other forms of the general expression for the potential energy in a capacitor, derivable from the expression on the last page by using V = Q/C to eliminate one of the three variables, V, Q, or C, from the equation: Where is the energy stored? Amazingly, in the electric field itself! For the parallel plate capacitor, which has a constant electric field, it is easy to calculate the energy in this field, starting from the second form above: The factor (Ad) is the volume of this capacitor. If we divide by this factor, the result will be the energy density, a general formula that applies (point by point) to all electric fields in a vacuum:

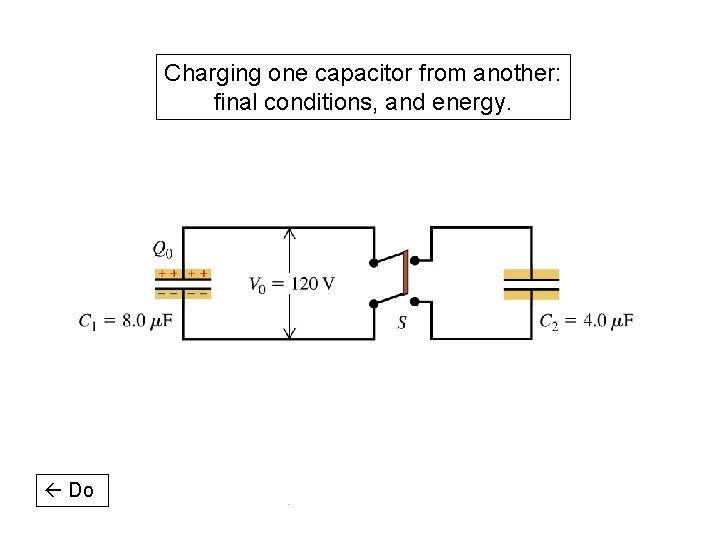
Charging one capacitor from another: final conditions, and energy. Do

Why have we been saying “in a vacuum”? If we fill the volume of any capacitor with a “dielectric” material, we will see the following: C 0 C For the same charge Q, the voltage on the capacitor in vacuum, V 0, will be greater than the voltage, V, on the same capacitor filled with dielectric. Since C = Q/V, the capacitance has been increased by V 0 /V. Very useful, but how does this happen?

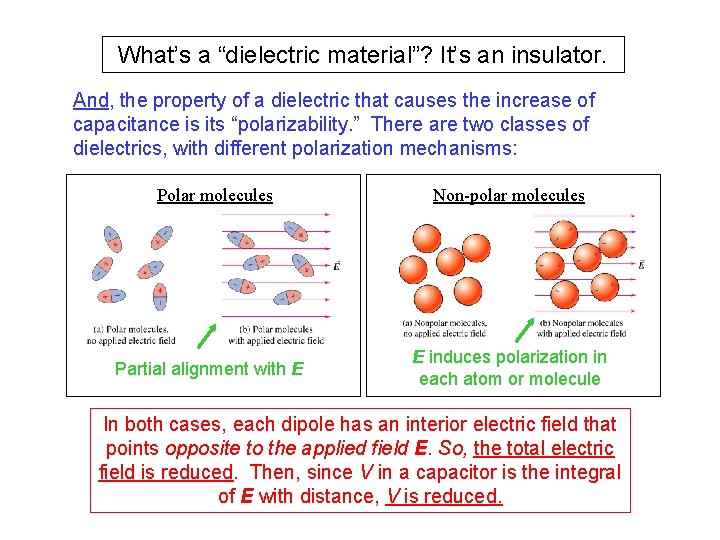
What’s a “dielectric material”? It’s an insulator. And, the property of a dielectric that causes the increase of capacitance is its “polarizability. ” There are two classes of dielectrics, with different polarization mechanisms: Polar molecules Partial alignment with E Non-polar molecules E induces polarization in each atom or molecule In both cases, each dipole has an interior electric field that points opposite to the applied field E. So, the total electric field is reduced. Then, since V in a capacitor is the integral of E with distance, V is reduced.

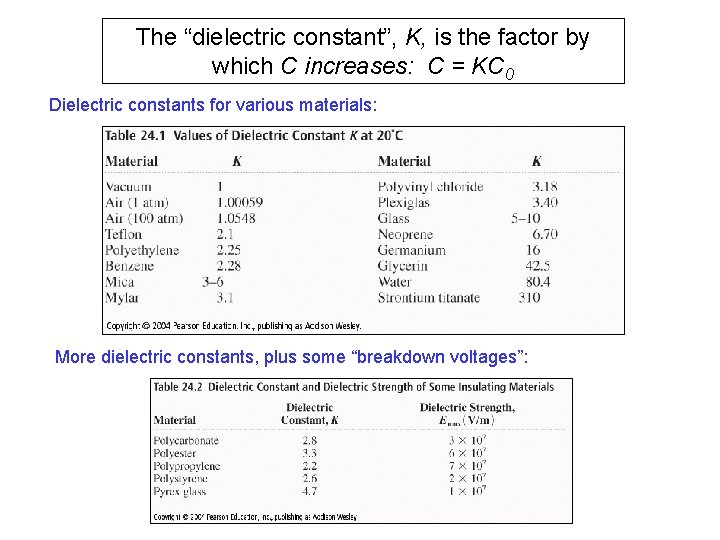
The “dielectric constant”, K, is the factor by which C increases: C = KC 0 Dielectric constants for various materials: More dielectric constants, plus some “breakdown voltages”:

Dielectrics in capacitors: bringing all the physics together First, consider a block of dielectric in an external field E. Essentially, the block is still net neutral inside, but the polarization has induced two surface charge densities, +/- si , with the negative surface charge on the “incoming” face, and the positive on the outgoing. Using the parallel plate capacitor as an example, putting this dielectric in the gap reduces the electric field as follows: (K > 1) The surface charges determine E 0 and E: Put these into the top equation to find si: If K is very large, si is approximatelys ! E 0 E

Dielectrics in capacitors, continued… Recall that e 0 is called the “permittivity of the vacuum”. We can imagine that the polarization of a dielectric changes this factor. So we define a permittivity for the material, e = Ke 0 that takes the polarization into account. Then we can modify the vacuum equations to apply to cases with dielectrics, simply by writing e in place of e 0. Showing how this works for a parallel plate capacitor: We have illustrated this simple replacement e 0 e for a parallel plate capacitor, but it applied to all capacitors, and to all equations involving permittivity.

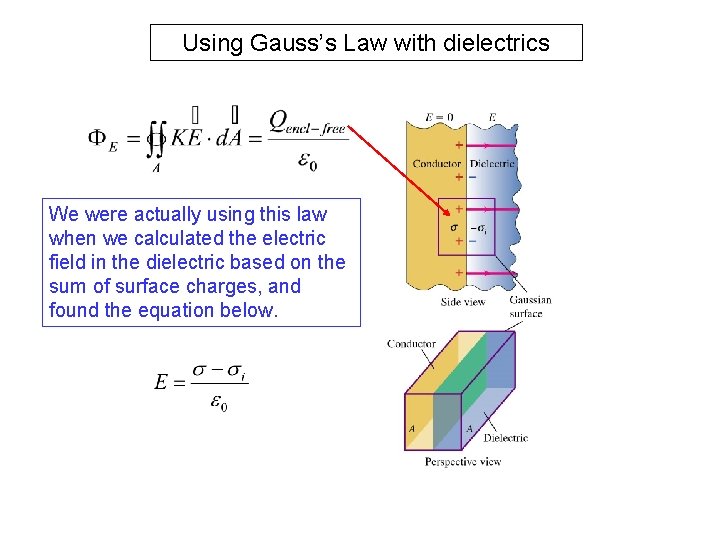
Using Gauss’s Law with dielectrics We were actually using this law when we calculated the electric field in the dielectric based on the sum of surface charges, and found the equation below.

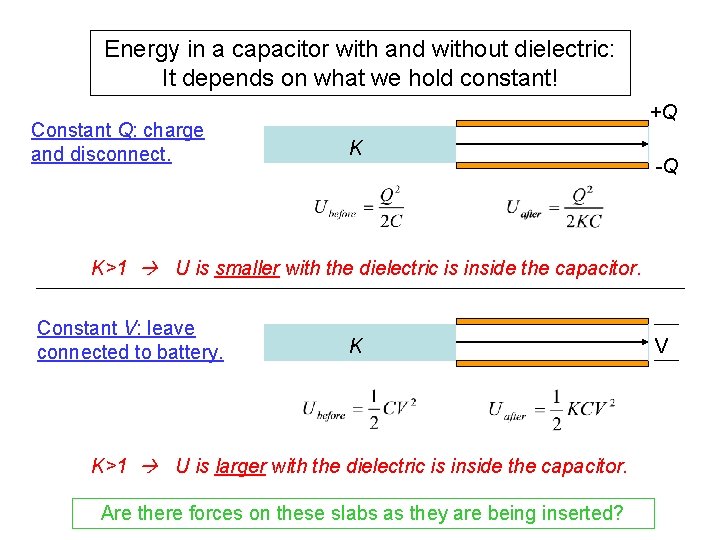
Energy in a capacitor with and without dielectric: It depends on what we hold constant! Constant Q: charge and disconnect. +Q K -Q K>1 U is smaller with the dielectric is inside the capacitor. Constant V: leave connected to battery. K K>1 U is larger with the dielectric is inside the capacitor. Are there forces on these slabs as they are being inserted? V

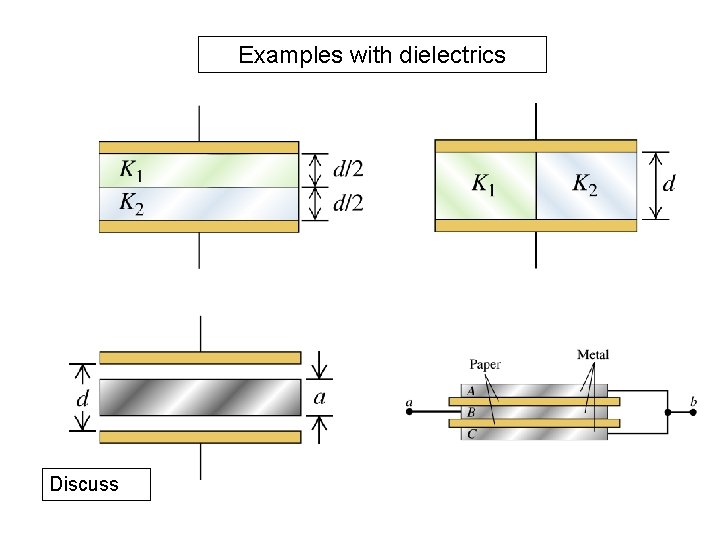
Examples with dielectrics Discuss

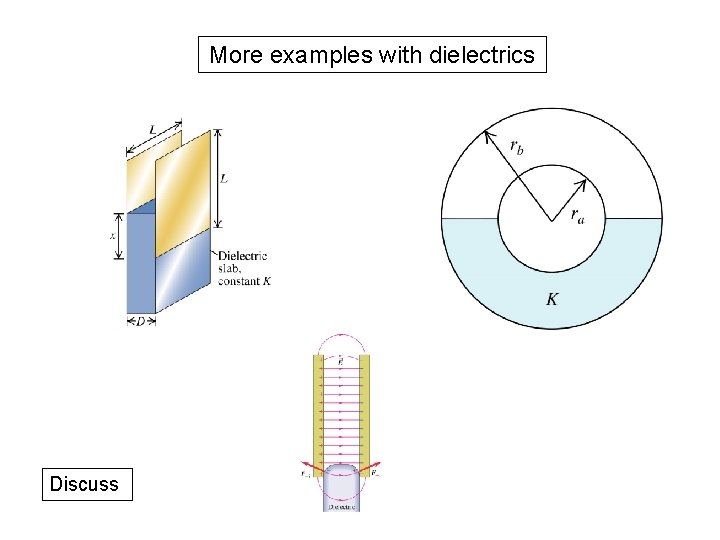
More examples with dielectrics Discuss

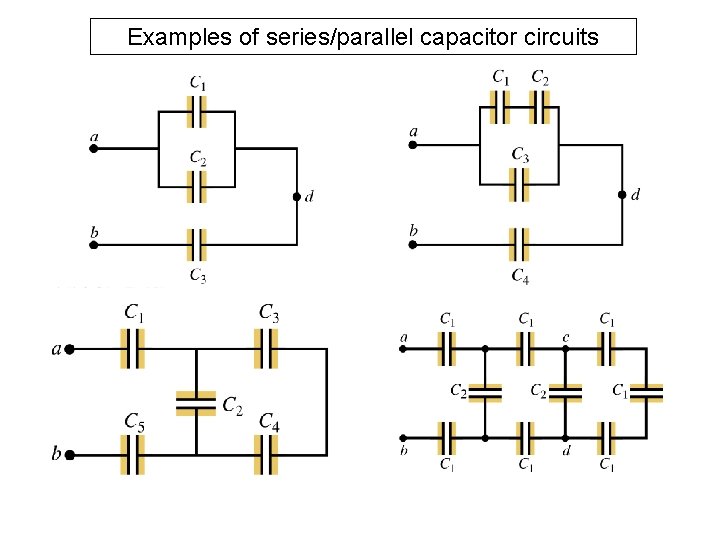
Examples of series/parallel capacitor circuits

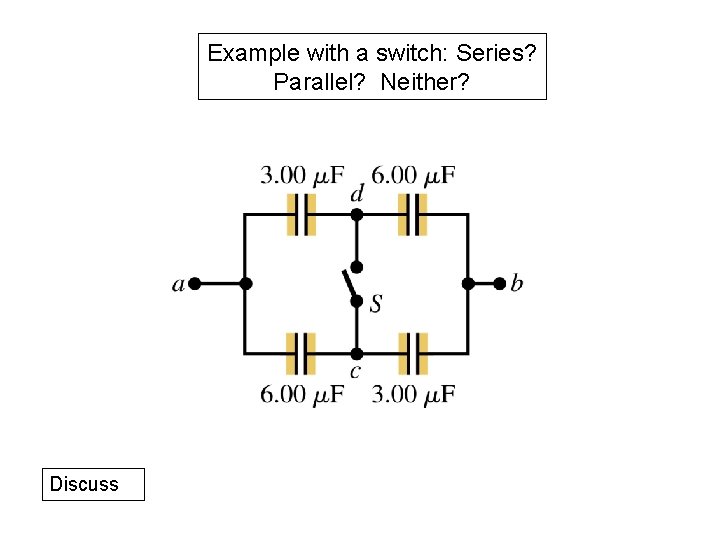
Example with a switch: Series? Parallel? Neither? Discuss

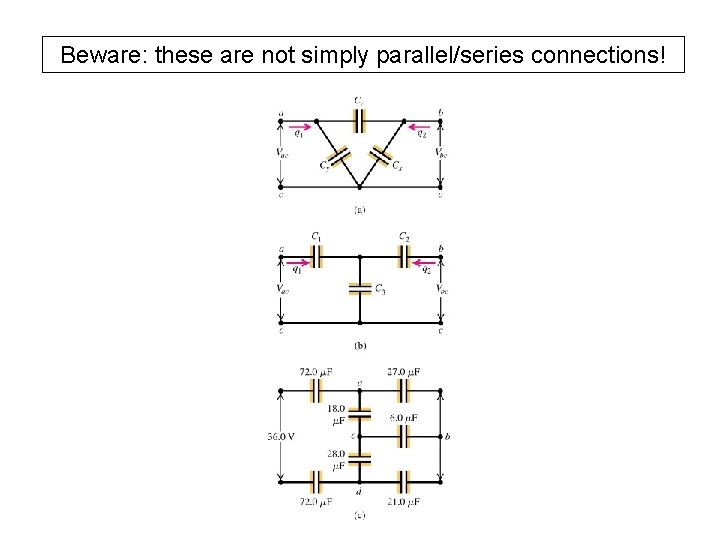
Beware: these are not simply parallel/series connections!