Capacitance The Ability to Store Charge Common Types

Capacitance The Ability to Store Charge

Common Types Electrolytic Tanalum Silver Mica
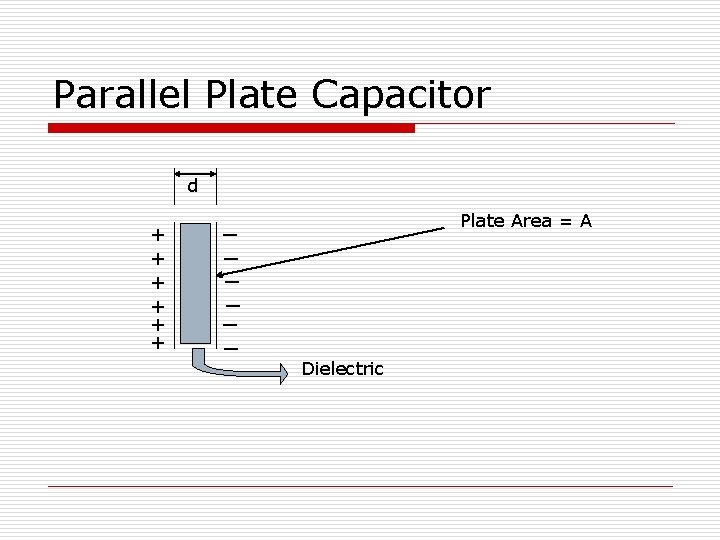
Parallel Plate Capacitor d + + + ― ― ― Plate Area = A Dielectric

Capacitance Depends on… o Separation of the plates (d) o Plate Area (A) [d in m] [A in m 2] o Dielectric Constant (e) [e in C 2/N-m 2]

Capacitance depends on the construction of the capacitor, not on the circuit it is used in.

Alternate Form for C Thus, C = Q/V Recall, V=W/Q

Example o What is the capacitance of a capacitor if the charge is 0. 075 C held at V = 400 V o C = Q/V =0. 075 C/400 V o = 1. 875 X 10 -4 f = 187. 5 mf

Storage of Charge o Charges flow from the wire to one plate of the capacitor. The insulator (dielectric) prevents charges from flowing to the other plate. Charge accumulates. o The accumulated charge attracts opposite charges on the other plate. o The second plate charge pushes opposite charges down the other wire. + + + ― ― ―

Capacitors in DC Circuits o Capacitor in a dc circuit n Capacitor will begin charging and current will flow n When fully charged (Q= CV), current stops o Electric field between plates cancels the field produced by the battery voltage

Dielectric Constant o Many texts give e in terms of a fundamental constant (eo) and a number that depends on the material (K) e = Keo eo = permittivity of free space = 8. 854 X 10 -12 C 2/Nm 2 K = dielectric constant
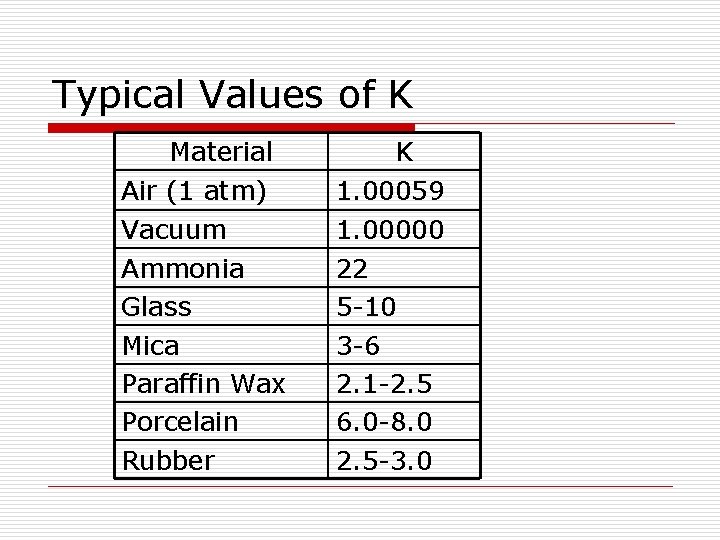
Typical Values of K Material Air (1 atm) K 1. 00059 Vacuum Ammonia Glass Mica Paraffin Wax Porcelain Rubber 1. 00000 22 5 -10 3 -6 2. 1 -2. 5 6. 0 -8. 0 2. 5 -3. 0

Example o Two rectangular sheets of copper foil 16 X 20 cm are separated by a thin layer of paraffin wax 0. 2 mm thick. Calculate the capacitance if the dielectric constant for the wax is 2. 4.

Combining Capacitance o Parallel – plates of the capacitors are at the same voltage as the poles of the battery. Voltage across AA’ = BB’ = E

Parallel Capacitance Q 1 = C 1 E Q 2 = C 2 E Q 3 = C 3 E Total Charge stored is… QT = Q 1 + Q 2 + Q 3 QT = E(C 1 + C 2 + C 3) = CTE CT = C 1 + C 2 + C 3

Series Capacitance The same current flows through each capacitor Current is charge/time, so Q 1 = Q 2 = Q 3 = QT

Series Capacitance o Kirchhoff’s Voltage Law n E = V 1 + V 2 + V 3

Try it o Adding Capacitance

Example Three capacitors of 2. 0, 3. 0, and 5. 0 mf are connected in parallel to a 12 V source. 1. Find the charge on each capacitor. 2. Find the total charge of the combination. 3. Find the total charge if the same three are connected in series to the 12 V source.

Solution (Parallel connection) 1. Q 1 = VC 1 = (12 V)(2. 0 X 10 -6 f) =24 m. C Q 2 = VC 2 = (12 V)(3. 0 X 10 -6 f) =36 m. C Q 3 = VC 3 = (12 V)(5. 0 X 10 -6 f) =60 m. C 2. QT = Q 1 + Q 2 + Q 3 = (24+36+60)m. C = 120 m. C

Solution (part 3) Series connection
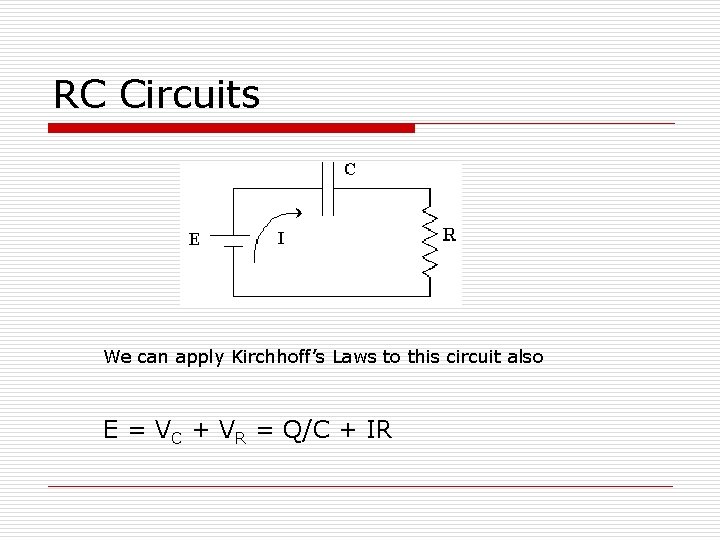
RC Circuits We can apply Kirchhoff’s Laws to this circuit also E = VC + VR = Q/C + IR

Charge Form o For a dc voltage flowing for a time t n I = Q/t n E = Q/C + QR/t = Q(1/C + R/t)

Current Form o Q = It o E = Q/C + IR = It/C + IR = I(t/C + R)

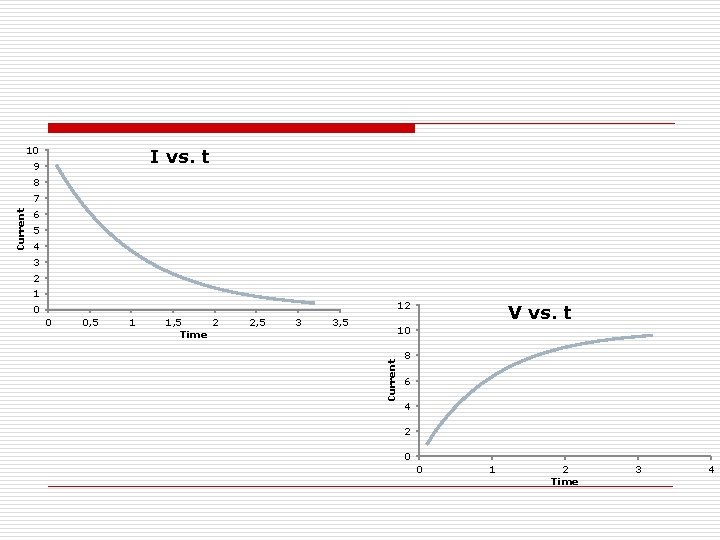
Time dependent forms o Notice that RC must have units of time – most books call this t = RC o Current o Voltage
10 I vs. t 9 8 6 5 4 3 2 1 12 0 0 0, 5 1 1, 5 2 Time 2, 5 3 3, 5 V vs. t 10 Current 7 8 6 4 2 0 0 1 2 Time 3 4

Saving Links o Charging Circuits o RC Circuit Applet
- Slides: 26