Capacitance Chapter 26 Electric Potential of Conductors V

Capacitance Chapter 26

Electric Potential of Conductors V 2 V 1 E=0 • The electric field E is zero within a conductor at equilibrium.

Electric Potential of Conductors V 2 V 1 E=0 • The electric field E is zero within a conductor at equilibrium. • Consequently the conductor has the same electric potential V everywhere inside.

Electric Potential of Conductors V 2 V 1 E=0 • The electric field E is zero within a conductor at equilibrium. • Consequently the conductor has the same electric potential V everywhere inside.

Electric Potential of Conductors V 2 V 1 E=0 • The electric field E is zero within a conductor at equilibrium. • Consequently the conductor has the same electric potential V everywhere inside. • The electric potential depends on how much excess charge has been added to the metal. The relationship between these quantities defines the capacitance.

Capacitance A capacitor consists of two pieces of metal carrying equal and opposite charges Q and –Q.

Capacitance A capacitor consists of two pieces of metal carrying equal and opposite charges Q and –Q. An electric potential difference V develops between the two pieces of metal.

Capacitance A capacitor consists of two pieces of metal carrying equal and opposite charges Q and –Q. An electric potential difference V develops between the two pieces of metal. It turns out that Q and V are proportional. The constant of proportionality is called the capacitance C.

Capacitance A capacitor consists of two pieces of metal carrying equal and opposite charges Q and –Q. An electric potential difference V develops between the two pieces of metal. It turns out that Q and V are proportional. The constant of proportionality is called the capacitance C. Q = CV [Units: Coulomb /Volt = Farad]

Capacitance A capacitor consists of two pieces of metal carrying equal and opposite charges Q and –Q. An electric potential difference V develops between the two pieces of metal. It turns out that Q and V are proportional. The constant of proportionality is called the capacitance C. Q = CV [Units: Coulomb /Volt = Farad] The capacitance C depends on the size and shape of the capacitor, and the material (if any) between them.

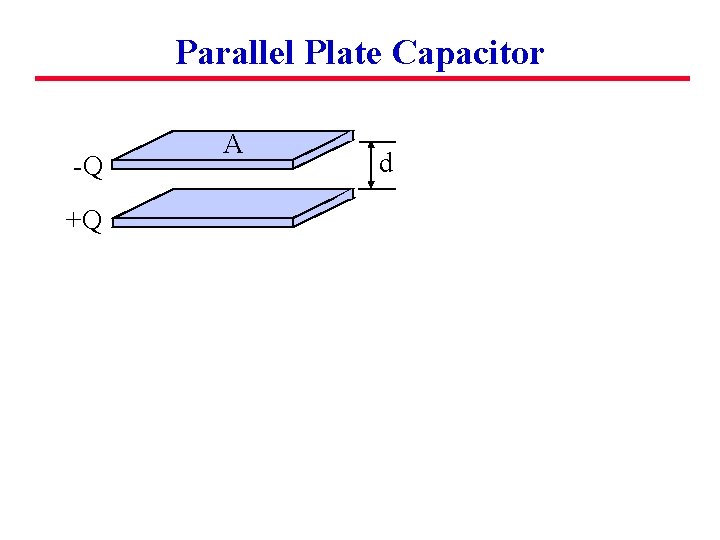
Parallel Plate Capacitor -Q +Q A d

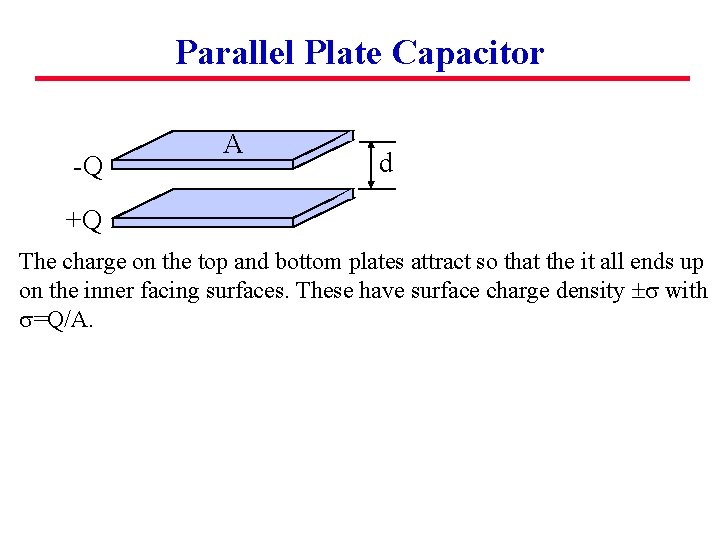
Parallel Plate Capacitor -Q A d +Q The charge on the top and bottom plates attract so that the it all ends up on the inner facing surfaces. These have surface charge density s with s=Q/A.

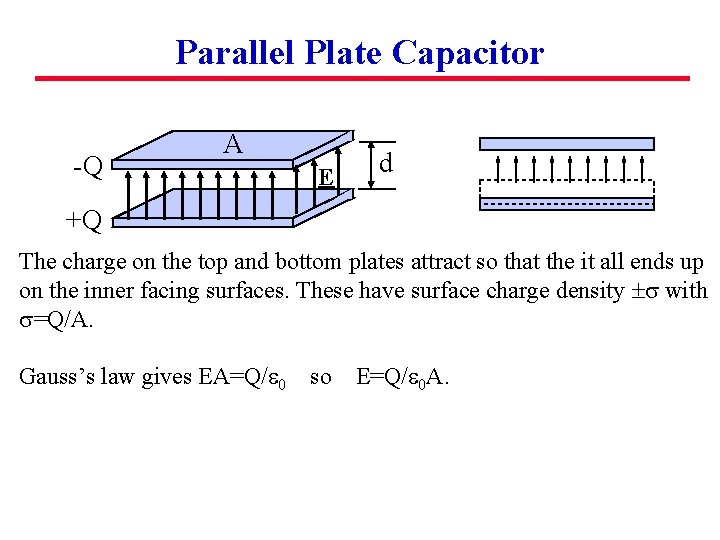
Parallel Plate Capacitor -Q A E d +Q The charge on the top and bottom plates attract so that the it all ends up on the inner facing surfaces. These have surface charge density s with s=Q/A.

Parallel Plate Capacitor -Q A E d +Q The charge on the top and bottom plates attract so that the it all ends up on the inner facing surfaces. These have surface charge density s with s=Q/A. Gauss’s law

Parallel Plate Capacitor -Q A E d +Q The charge on the top and bottom plates attract so that the it all ends up on the inner facing surfaces. These have surface charge density s with s=Q/A. Gauss’s law

Parallel Plate Capacitor -Q A E d +Q The charge on the top and bottom plates attract so that the it all ends up on the inner facing surfaces. These have surface charge density s with s=Q/A. Gauss’s law gives EA=Q/e 0 so E=Q/e 0 A.

Parallel Plate Capacitor -Q A E d +Q The charge on the top and bottom plates attract so that the it all ends up on the inner facing surfaces. These have surface charge density s with s=Q/A. Gauss’s law gives EA=Q/e 0 so E=Q/e 0 A. The potential difference between the two plates is ∆V=∫E·dl = Ed or ∆V = Qd/e 0 A.

Parallel Plate Capacitor -Q A E d +Q The charge on the top and bottom plates attract so that the it all ends up on the inner facing surfaces. These have surface charge density s with s=Q/A. Gauss’s law gives EA=Q/e 0 so E=Q/e 0 A. The potential difference between the two plates is ∆V=∫E·dl = Ed or ∆V = Qd/e 0 A. Turning this about gives Q = (e 0 A/d)∆V i. e. Q=C∆V with C=e 0 A/d.

Parallel Plate Capacitor -Q A E d +Q Q=C∆V with C= e 0 A/d The capacitance is like the capacity of the object to hold charge. Bigger C means the object can hold more charge (at a given ∆V). The capacitance is proportional to the area A (more capacity) and inversely proportional to the separation d (smaller ∆V=Ed for given Q).

How Do You Get Q and -Q? Q -Q

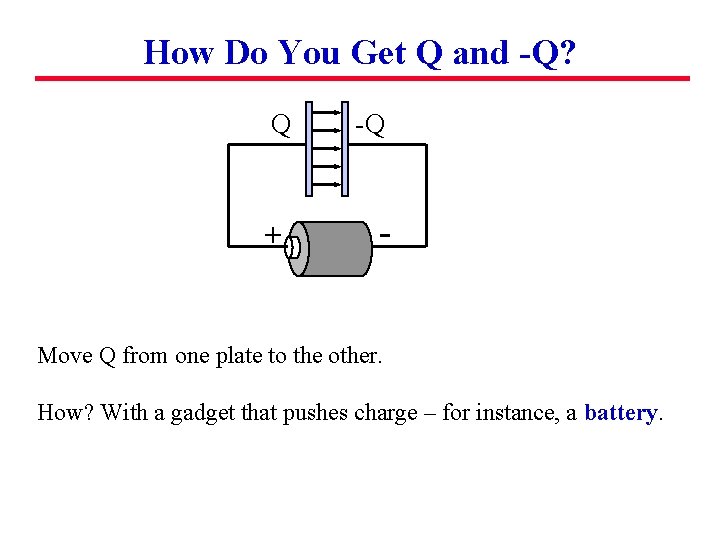
How Do You Get Q and -Q? Q -Q Move Q from one plate to the other. How?

How Do You Get Q and -Q? Q -Q + - Move Q from one plate to the other. How? With a gadget that pushes charge – for instance, a battery.

How Do You Get Q and -Q? Q -Q + - Move Q from one plate to the other. How? With a gadget that pushes charge – for instance, a battery. Hooked to metal plates, a 1. 5 Volt battery moves charge until the potential difference between the plates is also 1. 5 V.

How Do You Get Q and -Q? Q -Q + - Q -Q A battery is like a charge escalator. With just a wire between the plates, the charges making up Q would repel each other and run through the wire to neutralize -Q. But the battery pushes the charges “uphill. ”

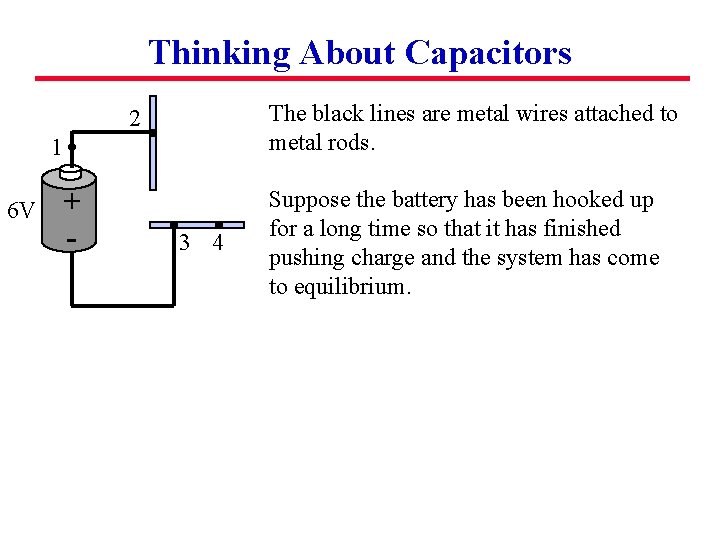
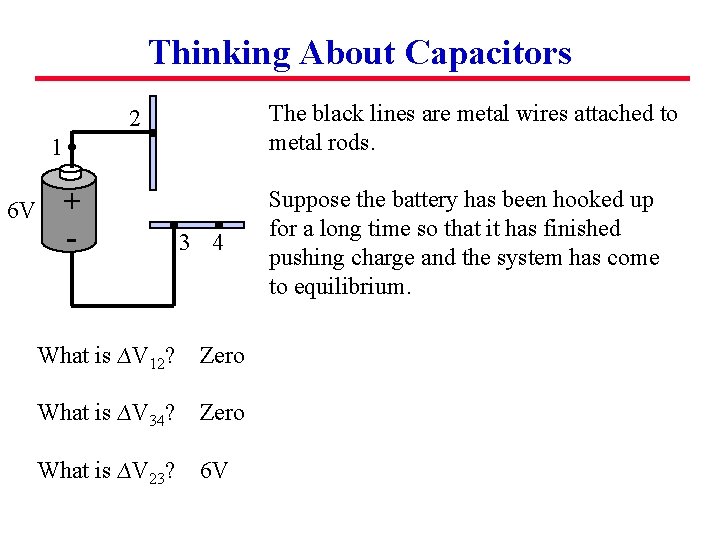
Thinking About Capacitors The black lines are metal wires attached to metal rods. 2 1 + - 6 V 3 4 Suppose the battery has been hooked up for a long time so that it has finished pushing charge and the system has come to equilibrium.

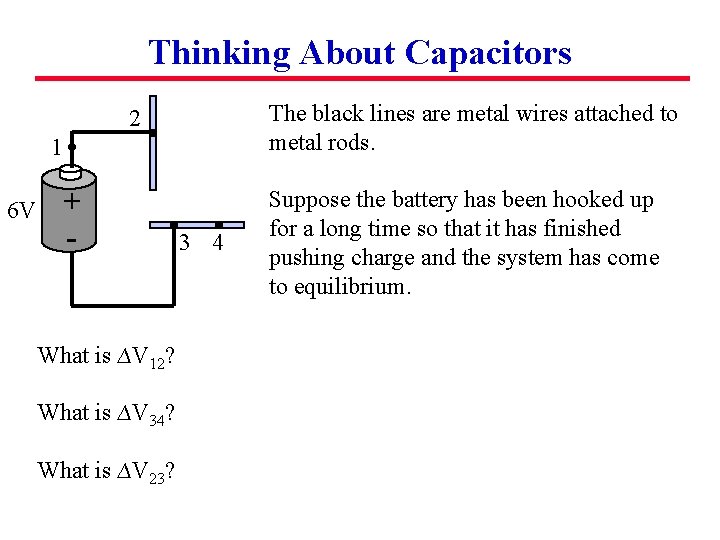
Thinking About Capacitors The black lines are metal wires attached to metal rods. 2 1 + - 6 V What is ∆V 12? What is ∆V 34? What is ∆V 23? 3 4 Suppose the battery has been hooked up for a long time so that it has finished pushing charge and the system has come to equilibrium.

Thinking About Capacitors The black lines are metal wires attached to metal rods. 2 1 + - 6 V 3 4 What is ∆V 12? Zero What is ∆V 34? Zero What is ∆V 23? 6 V Suppose the battery has been hooked up for a long time so that it has finished pushing charge and the system has come to equilibrium.

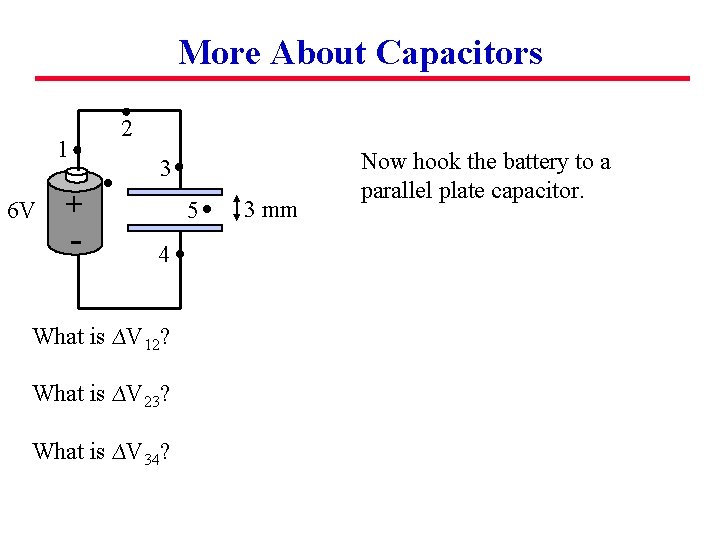
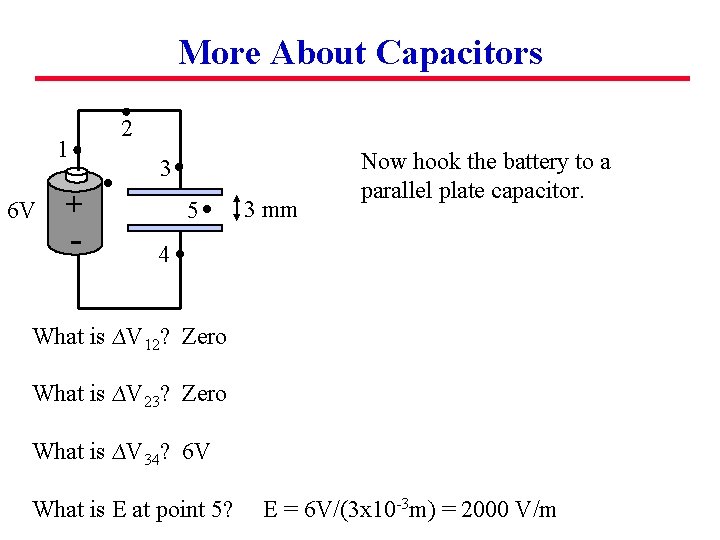
More About Capacitors 2 1 6 V 3 + - 5 4 What is ∆V 12? What is ∆V 23? What is ∆V 34? 3 mm Now hook the battery to a parallel plate capacitor.

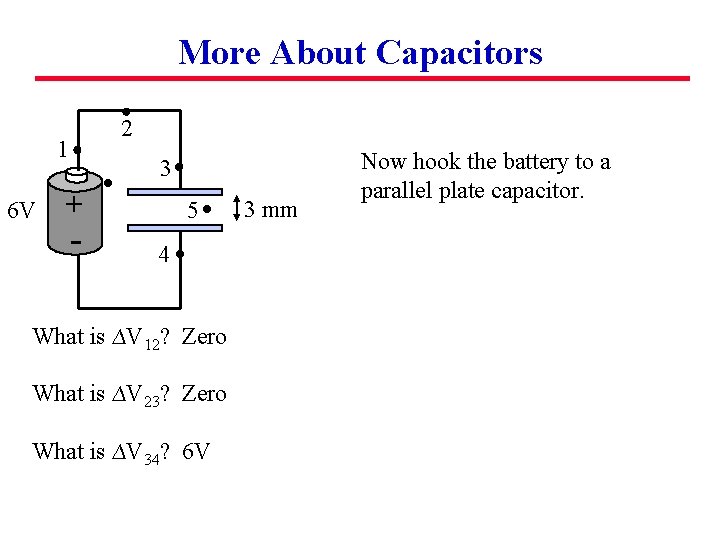
More About Capacitors 2 1 6 V 3 + - 5 4 What is ∆V 12? Zero What is ∆V 23? Zero What is ∆V 34? 6 V 3 mm Now hook the battery to a parallel plate capacitor.

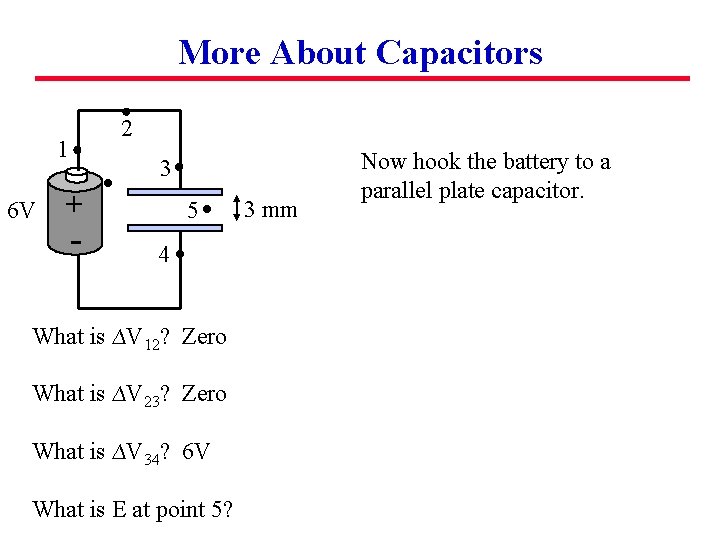
More About Capacitors 2 1 6 V 3 + - 5 4 What is ∆V 12? Zero What is ∆V 23? Zero What is ∆V 34? 6 V What is E at point 5? 3 mm Now hook the battery to a parallel plate capacitor.

More About Capacitors 2 1 6 V 3 + - 5 3 mm Now hook the battery to a parallel plate capacitor. 4 What is ∆V 12? Zero What is ∆V 23? Zero What is ∆V 34? 6 V What is E at point 5? E = 6 V/(3 x 10 -3 m) = 2000 V/m

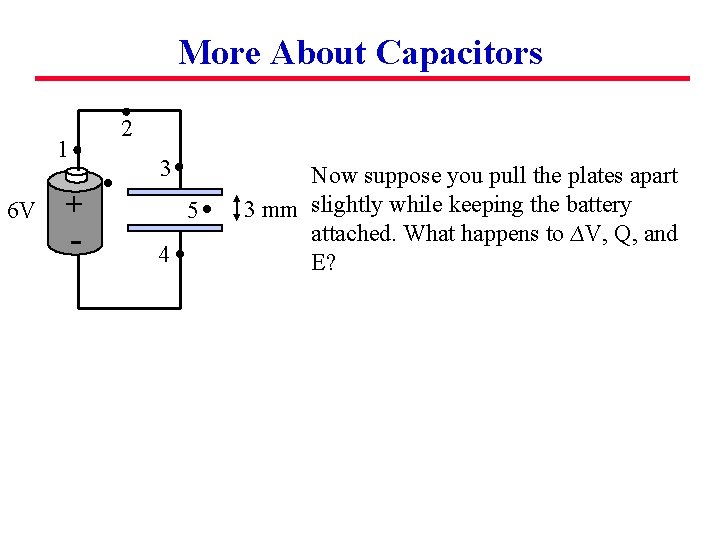
More About Capacitors 2 1 6 V 3 + - 5 4 Now suppose you pull the plates apart 3 mm slightly while keeping the battery attached. What happens to ∆V, Q, and E?

More About Capacitors 2 1 6 V 3 + - 5 4 Now suppose you pull the plates apart 3 mm slightly while keeping the battery attached. What happens to ∆V, Q, and E? ∆V depends on the battery: it stays at 6 V.

More About Capacitors 2 1 6 V 3 + - 5 4 Now suppose you pull the plates apart 3 mm slightly while keeping the battery attached. What happens to ∆V, Q, and E? ∆V depends on the battery: it stays at 6 V. Use Q=C∆V. Here C=e 0 A/d decreases so Q decreases.

More About Capacitors 2 1 6 V 3 + - 5 4 Now suppose you pull the plates apart 3 mm slightly while keeping the battery attached. What happens to ∆V, Q, and E? ∆V depends on the battery: it stays at 6 V. Use Q=C∆V. Here C=e 0 A/d decreases so Q decreases. E= ∆V / (new length) gets smaller.

What Does a Capacitor Do? • Stores electrical charge. • Stores electrical energy. Capacitors are used when a sudden release of energy is needed (such as in a photographic flash). Capacitors are basic elements of electrical circuits both macroscopic (as discrete elements) and microscopic (as parts of integrated circuits).

What Does a Capacitor Do? • Stores electrical charge. • Stores electrical energy. The charge is easy to see. If a certain potential, ∆V, is applied to a capacitor C, it must store a charge Q=C∆V: -Q +Q C ∆V (Symbol for a capacitor)

Energy Stored in a Capacitor • Build the charge up a little at a time, letting the charge q on the plate grow from 0 to Q.

Energy Stored in a Capacitor • Build the charge up a little at a time, letting the charge q on the plate grow from 0 to Q. • When the charge is q the potential is V=q/C.

Energy Stored in a Capacitor • Build the charge up a little at a time, letting the charge q on the plate grow from 0 to Q. • When the charge is q the potential is V=q/C. • Now transfer a little more charge dq.

Energy Stored in a Capacitor • Build the charge up a little at a time, letting the charge q on the plate grow from 0 to Q. • When the charge is q the potential is V=q/C. • Now transfer a little more charge dq. • This requires a work d. W = Vdq = (1/C) q dq.

Energy Stored in a Capacitor • Build the charge up a little at a time, letting the charge q on the plate grow from 0 to Q. • When the charge is q the potential is V=q/C. • Now transfer a little more charge dq. • This requires a work d. W = Vdq = (1/C) q dq. • Integrating q from 0 to Q gives the total stored (potential) electric energy:

Energy Stored in a Capacitor • Build the charge up a little at a time, letting the charge q on the plate grow from 0 to Q. • When the charge is q the potential is V=q/C. • Now transfer a little more charge dq. • This requires a work d. W = Vdq = (1/C) q dq. • Integrating q from 0 to Q gives the total stored (potential) electric energy:

Energy Density +Q ∆V -Q • Look at an energy density, i. e. , energy per unit volume. • For the parallel plate capacitor the volume is Ad, so u. E= U/(Ad) = (1/2 C∆V 2)/Ad • Now also use C = e 0 A/d. Then u. E = (e 0/2)(∆V/d)2 = (e 0/2)E 2

Energy Density +Q V -Q u. E = (e 0/2)(∆V/d)2 = (e 0/2)E 2 • This leads to another way to understand the energy. • We can think of the energy as stored in the FIELD, rather than in the plates. • If an electric field exists, then you can associate an electric potential energy density of (e 0/2)E 2.