Capacitance and Electric Fields Chapter 13 Introduction Capacitors

Capacitance and Electric Fields Chapter 13 § Introduction § Capacitors and Capacitance § Alternating Voltages and Currents § The Effect of a Capacitor’s Dimensions § Electric Fields § Capacitors in Series and Parallel § Voltage and Current § Sinusoidal Voltages and Currents § Energy Stored in a Charged Capacitor § Circuit Symbols Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 1

Introduction 13. 1 § We noted earlier that an electric current represents a flow of charge § A capacitor can store electric charge and can therefore store electrical energy § Capacitors are often used in association with alternating currents and voltages § They are a key component in almost all electronic circuits Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 2

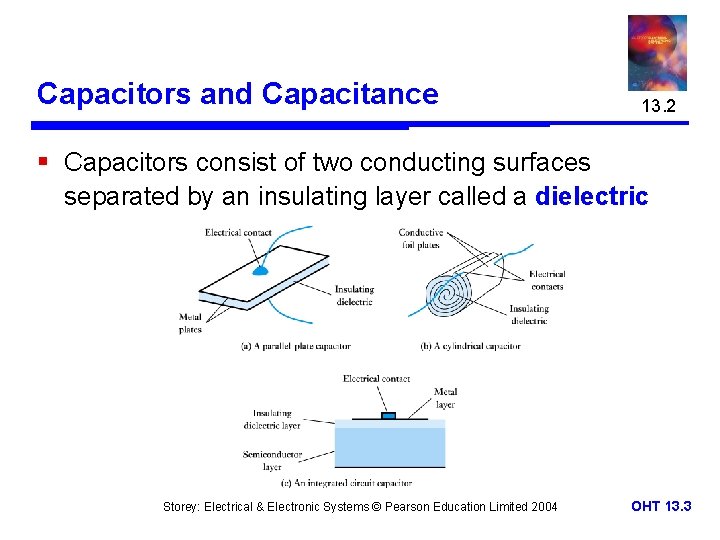
Capacitors and Capacitance 13. 2 § Capacitors consist of two conducting surfaces separated by an insulating layer called a dielectric Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 3

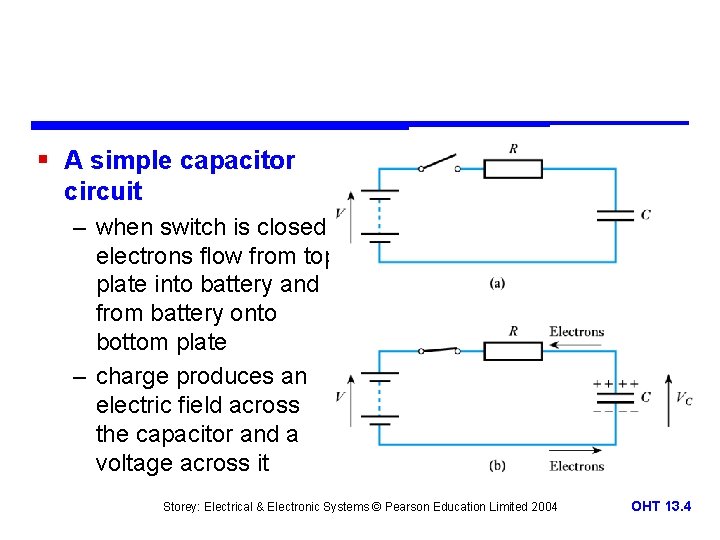
§ A simple capacitor circuit – when switch is closed electrons flow from top plate into battery and from battery onto bottom plate – charge produces an electric field across the capacitor and a voltage across it Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 4

§ For a given capacitor the stored charge q is directly proportional to the voltage across it V § The constant of proportionality is the capacitance C and thus § If the charge is measured in coulombs and the voltage in volts, then the capacitance is in farads Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 5

§ Example – see Example 13. 1 in course text A 10 F capacitor has 10 V across it. What quantity of charge is stored in it? From above Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 6

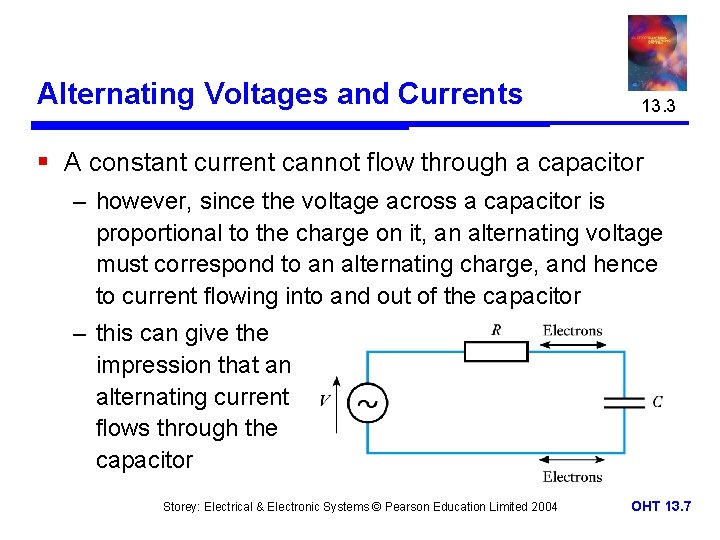
Alternating Voltages and Currents 13. 3 § A constant current cannot flow through a capacitor – however, since the voltage across a capacitor is proportional to the charge on it, an alternating voltage must correspond to an alternating charge, and hence to current flowing into and out of the capacitor – this can give the impression that an alternating current flows through the capacitor Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 7

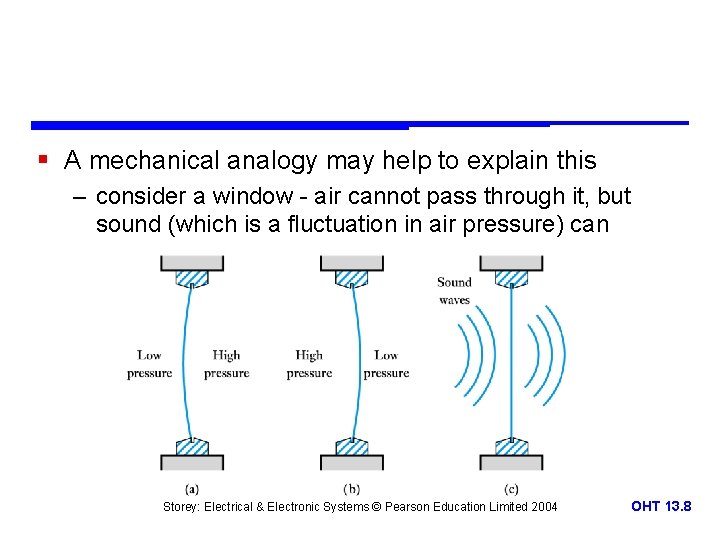
§ A mechanical analogy may help to explain this – consider a window - air cannot pass through it, but sound (which is a fluctuation in air pressure) can Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 8

The Effect of a Capacitor’s Dimensions 13. 4 § The capacitance of a capacitor is directly proportional to its area A, and inversely proportional to the distance between its plates d. Hence C A/d – the constant of proportionality is the permittivity of the dielectric – the permittivity is normally expressed as the product of the absolute permittivity 0 and the relative permittivity r of the dielectric used Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 9

Electric Fields 13. 5 § The charge on the capacitor produces an electric field with an electric field strength E given by the units of E are volts/metre (V/m) Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 10

§ All insulating materials have a maximum value for the field strength that they can withstand – the dielectric strength Em § To produce maximum capacitance for a given size of capacitor we want d to be as small as possible – however, as d is decreased the electric field E is increased – if E exceed Em the dielectric will break down – there is therefore a compromise between physical size and breakdown voltage Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 11

§ The force between positive and negative charges is described in terms of the electric flux linking them – measured in coulombs (as for electric charge) – a charge Q will produce a total flux of Q coulombs § We also define the electric flux density D as the flux per unit area § In a capacitor we can almost always ignore edge effects, and Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 12

§ Combining the earlier equations it is relatively easy to show that § Thus the permittivity of the dielectric within a capacitor is equal to the ratio of the electric flux density to the electric field strength. Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 13

Capacitors in Series and Parallel 13. 6 § Capacitors in parallel – consider a voltage V applied across two capacitors – then the charge on each is – if the two capacitors are replaced with a single capacitor C which has a similar effect as the pair, then Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 14

§ Capacitors in series – consider a voltage V applied across two capacitors in series – the only charge that can be applied to the lower plate of C 1 is that supplied by the upper plate of C 2. Therefore the charge on each capacitor must be identical. Let this be Q, and therefore if a single capacitor C has the same effect as the pair, then Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 15

Voltage and Current 13. 7 § The voltage across a capacitor is directly related to the charge on the capacitor § Alternatively, since Q = CV we can see that and since d. Q/dt is equal to current, it follows that Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 16

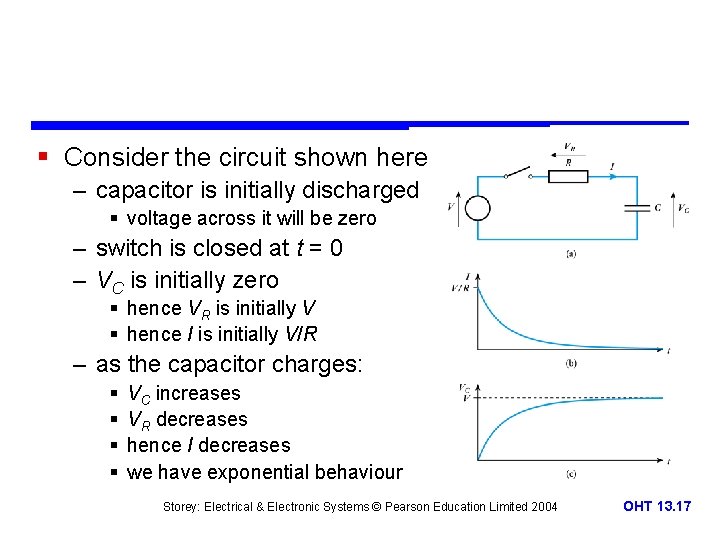
§ Consider the circuit shown here – capacitor is initially discharged § voltage across it will be zero – switch is closed at t = 0 – VC is initially zero § hence VR is initially V § hence I is initially V/R – as the capacitor charges: § § VC increases VR decreases hence I decreases we have exponential behaviour Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 17

§ Time constant – charging current is determined by R and the voltage across it – increasing R will increase the time taken to charge C – increasing C will also increase time taken to charge C – time required to charge to a particular voltage is determined by the product CR – this product is the time constant (greek tau) § See Computer Simulation Exercises 13. 1 and 13. 2 in the course text Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 18

Sinusoidal Voltages and Currents 13. 8 § Consider the application of a sinusoidal voltage to a capacitor – from above I = C d. V/dt – current is directly proportional to the differential of the voltage – the differential of a sine wave is a cosine wave – the current is phase-shifted by 90 with respect to the voltage Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 19

§ Since I = C d. V/dt the magnitude of the current is related to the rate of change of the voltage – in sinusoidal voltages the rate of change is determined by the frequency – hence capacitors are frequency dependent in their characteristics § We will return to look at frequency dependence in later lectures. Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 20

Energy Stored in a Charged Capacitor 13. 9 § To move a charge Q through a potential difference V requires an amount of energy QV § As we charge up a capacitor we repeatedly add small amounts of charge Q by moving them through a voltage equal to the voltage on the capacitor § Since Q = CV, it follows that Q = C V, so the energy needed E is given by Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 21

§ Alternatively, since V = Q/C § Example – see Example 13. 7 in the course text Calculate the energy stored in a 10 F capacitor when it is charged to 100 V. From above: Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 22

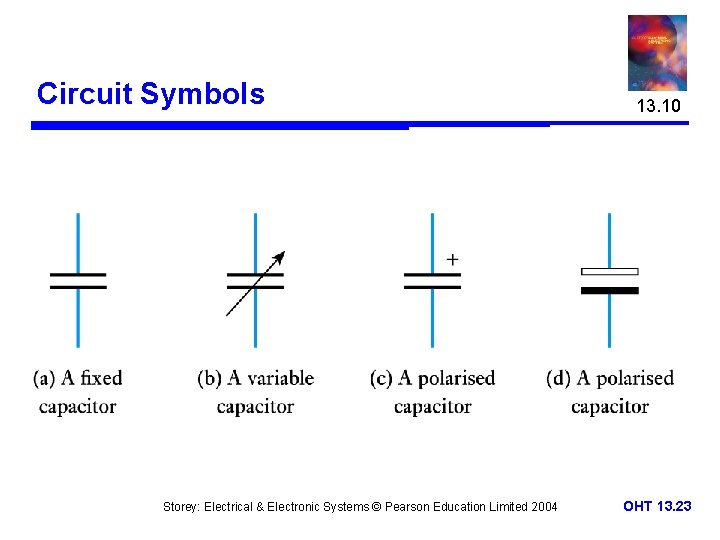
Circuit Symbols Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 13. 10 OHT 13. 23

Key Points § § A capacitor consists of two plates separated by a dielectric The charge stored on a capacitor is proportional to V A capacitor blocks DC but appears to pass AC The capacitance of several capacitors in parallel is equal to the sum of their individual capacitances § The capacitance of several capacitors in series is equal to the reciprocal of the sum of the reciprocals of the individual capacitances § In AC circuits current leads voltage by 90 in a capacitor § The energy stored in a capacitor is ½CV 2 or ½Q 2/C Storey: Electrical & Electronic Systems © Pearson Education Limited 2004 OHT 13. 24