Capability analysis 2 WS 02 Industrial Statistics A

Capability analysis 2 WS 02 Industrial Statistics A. Di Bucchianico /k
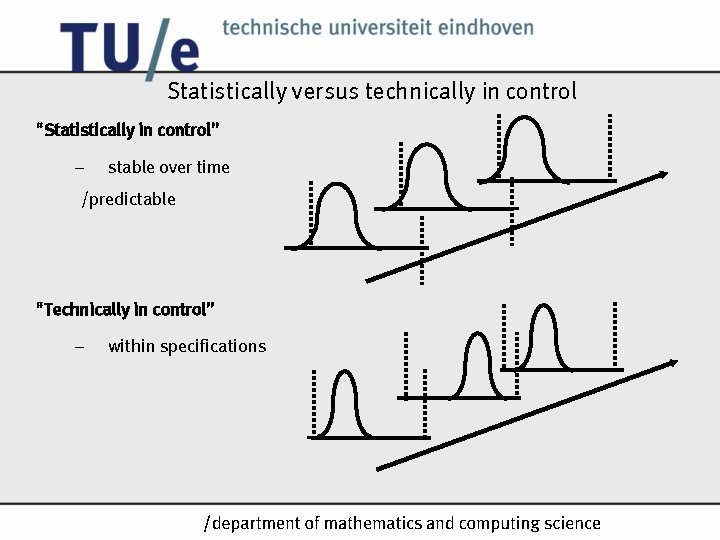
Statistically versus technically in control “Statistically in control” – stable over time /predictable “Technically in control” – within specifications /k
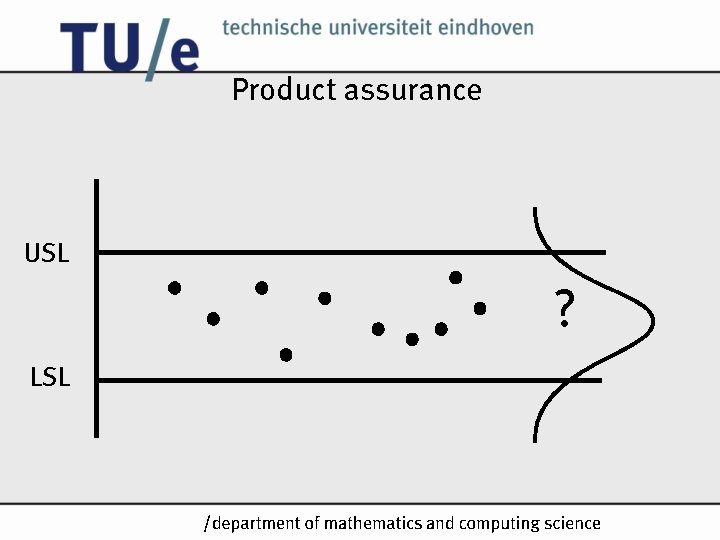
Product assurance USL ? LSL /k
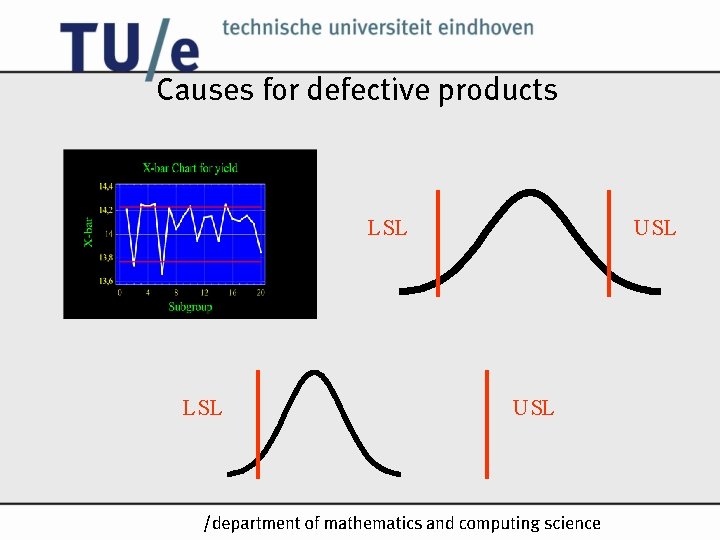
Causes for defective products LSL USL /k

The Process Capability Study (PCS) Questions: LSL N • how well does the process spread fit in between the specification limits? • how well is the process centred between the specification limits? • which measurements should be taken? PCS is only meaningful when the process is statistically in control! /k USL

Major uses of Process Capability Study • Predicting how well the process will satisfy the specifications • Assisting product developers/designers in selecting or modifying a process • Specifying performance requirements for new equipment • Selecting between competing vendors • Testing a new process /k

Control charts vs capability analysis type of control tool statistical control chart technical control process capability study /k

PCS step by step 1. Prepare and measure 2. Check whether data are normally distributed 3. Calculate capability indices 4. Conclusions and actions /k

PCS step 1: Prepare and Measure • Quality should be sufficiently measurable • Measuring equipment precise enough • At least 50, preferably 100 single measurements • No adjustments to process • Record circumstances • Record order and if possible time of measurements /k
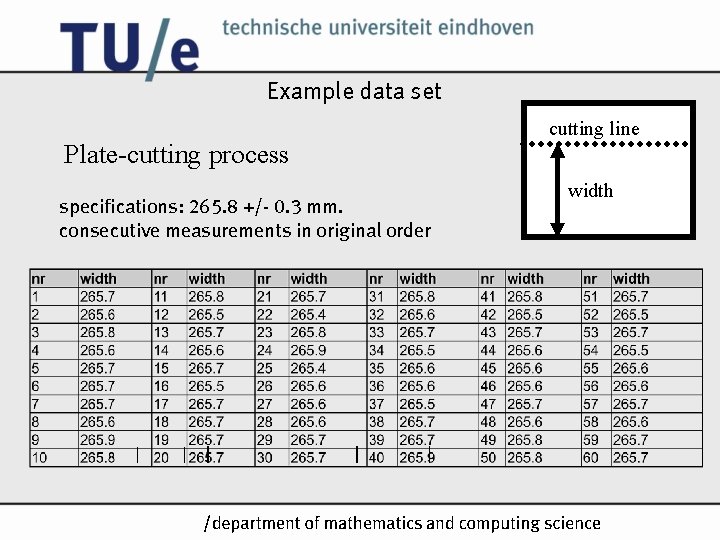
Example data set Plate-cutting process specifications: 265. 8 +/- 0. 3 mm. consecutive measurements in original order cutting line width /k

PCS step 2: check distribution Check for normality: • graphical: – histogram, better: density trace – normal probability plot (graphical) • formal: – Shapiro Wilks test /k
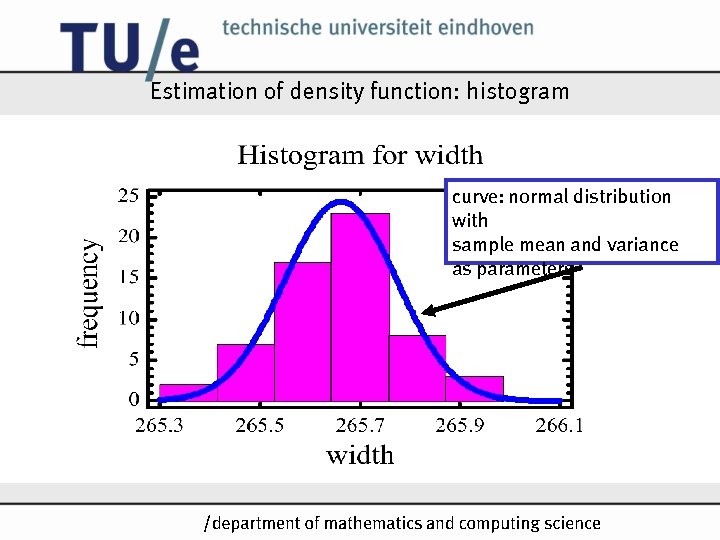
Estimation of density function: histogram curve: normal distribution with sample mean and variance as parameters /k

Drawbacks of the histogram • misused for investigating normality • time ordering of data is lost • shape depends heavily on bin width + bin location: Histogram for strength 5 frequency 4 same data set 3 2 1 0 24 29 34 39 44 49 54 strength • shape is stable for data sets of size 75 or larger • optimal number of bins n /k

Alternative to histogram: Density Trace (also called naive density estimator): • use moving bins instead of fixed bins • choose bin width (automatically in Statgraphics) • count number of observations in bin at each point • divide by length of bin /k
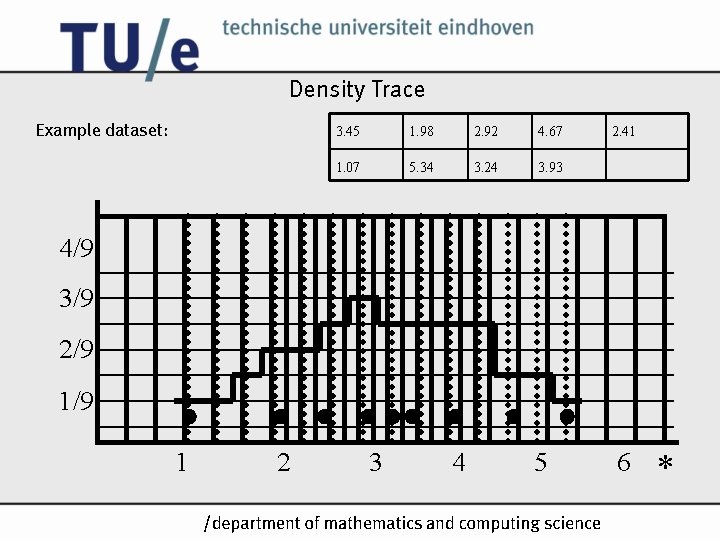
Density Trace Example dataset: 3. 45 1. 98 2. 92 4. 67 1. 07 5. 34 3. 24 3. 93 2. 41 4/9 3/9 2/9 1 2 3 4 5 /k 6 *
Density Trace of plate-width /k
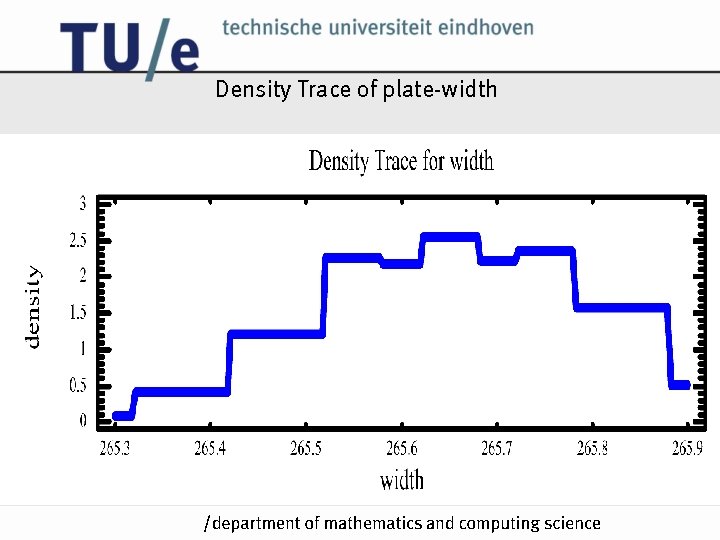
Density Trace of plate-width /k
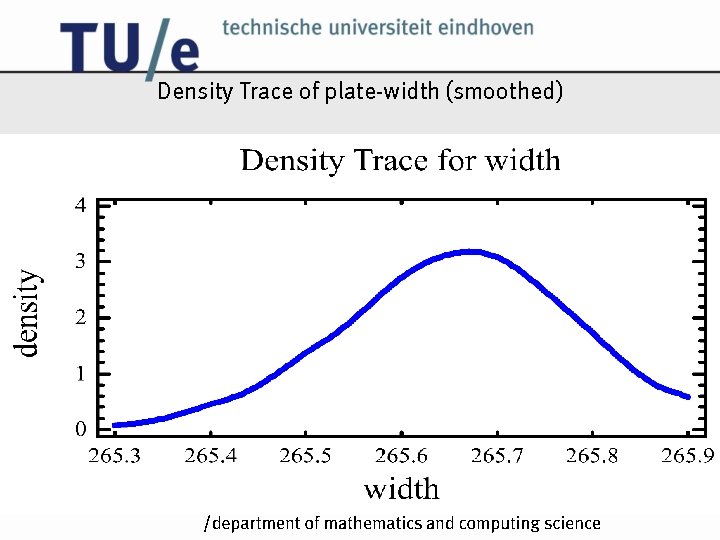
Density Trace of plate-width (smoothed) /k
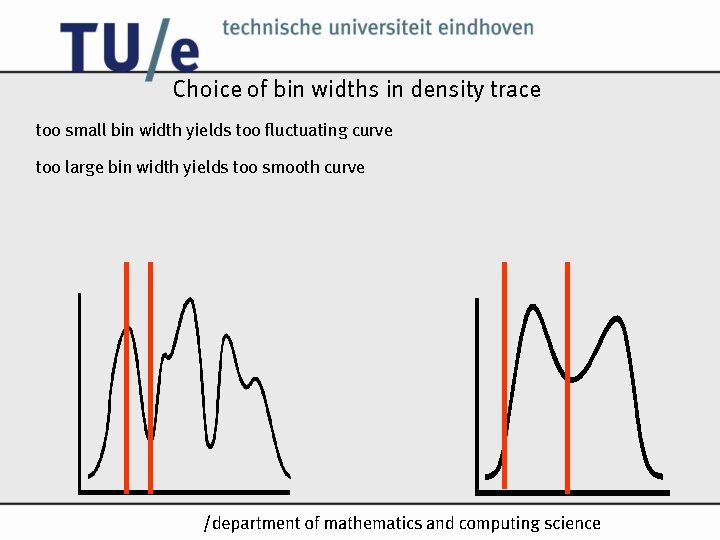
Choice of bin widths in density trace too small bin width yields too fluctuating curve too large bin width yields too smooth curve /k
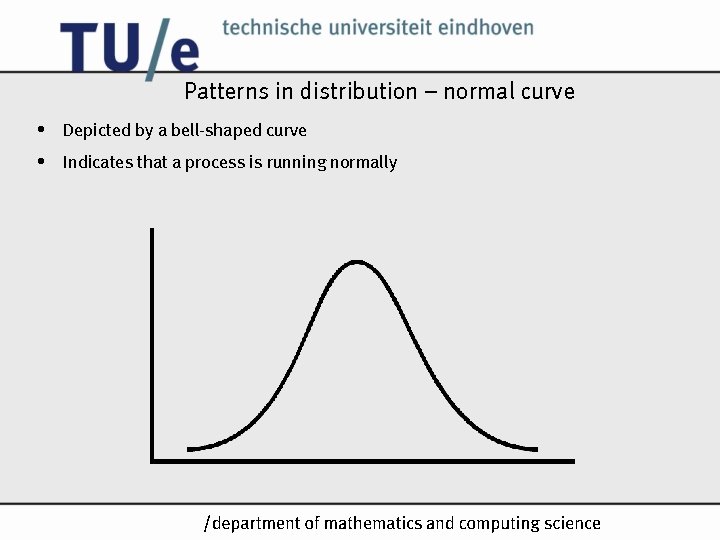
Patterns in distribution – normal curve • Depicted by a bell-shaped curve • Indicates that a process is running normally /k
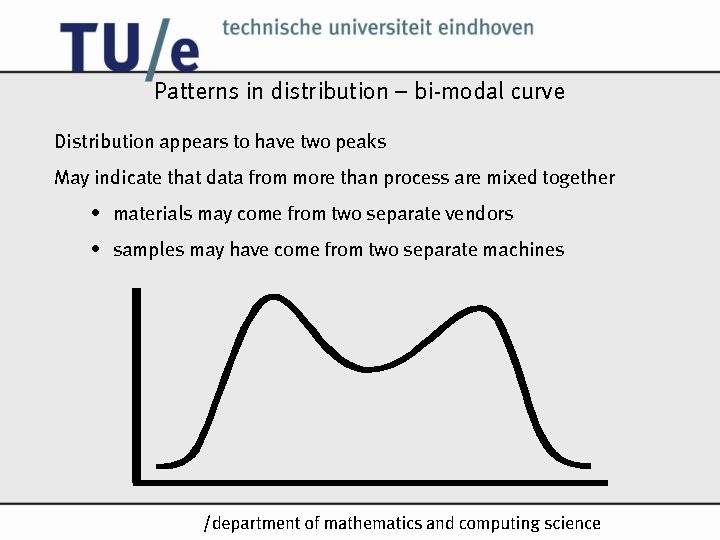
Patterns in distribution – bi-modal curve Distribution appears to have two peaks May indicate that data from more than process are mixed together • materials may come from two separate vendors • samples may have come from two separate machines /k
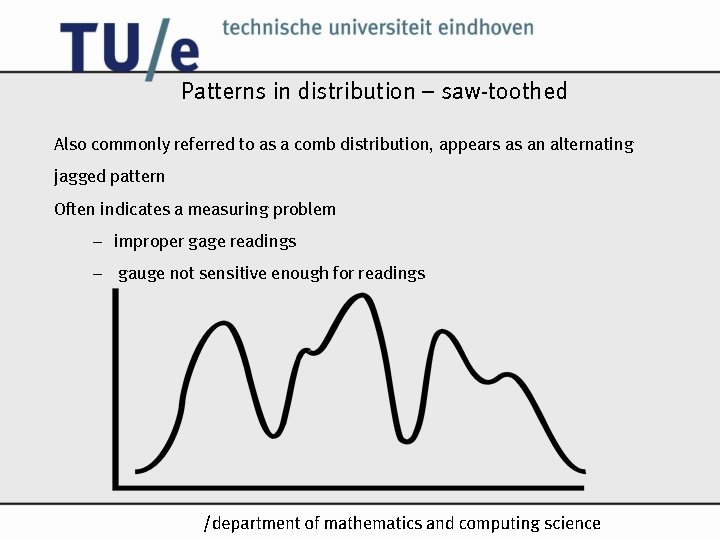
Patterns in distribution – saw-toothed Also commonly referred to as a comb distribution, appears as an alternating jagged pattern Often indicates a measuring problem – improper gage readings – gauge not sensitive enough for readings /k
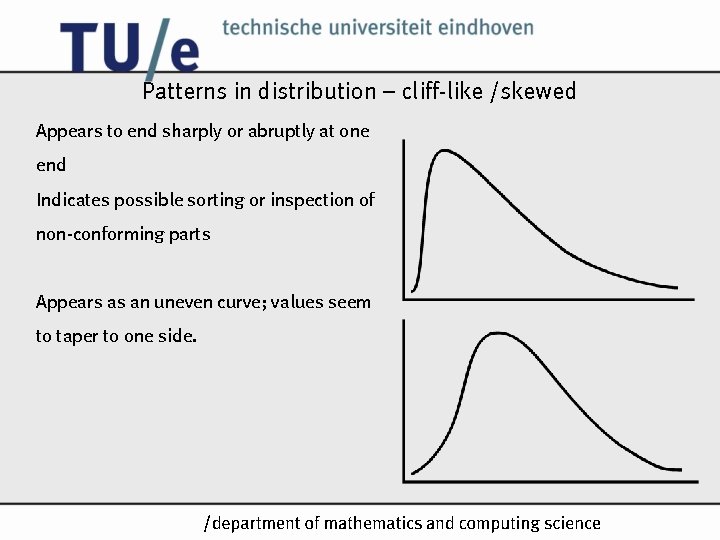
Patterns in distribution – cliff-like /skewed Appears to end sharply or abruptly at one end Indicates possible sorting or inspection of non-conforming parts Appears as an uneven curve; values seem to taper to one side. /k
Testing normality /k
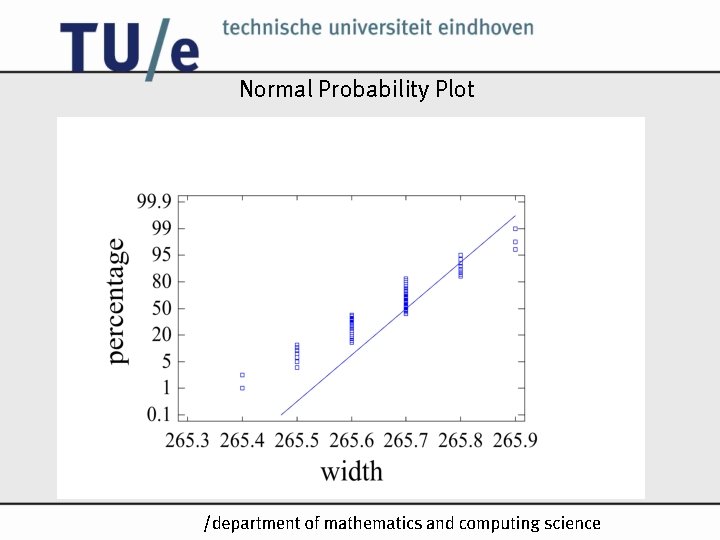
Normal Probability Plot /k
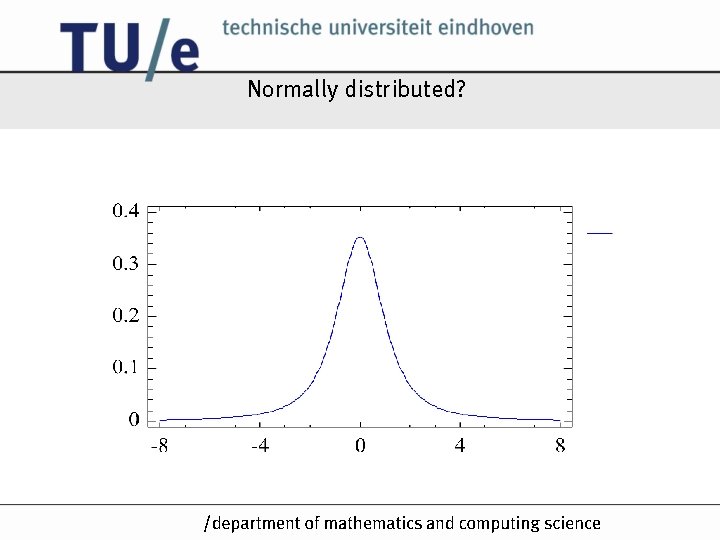
Normally distributed? /k
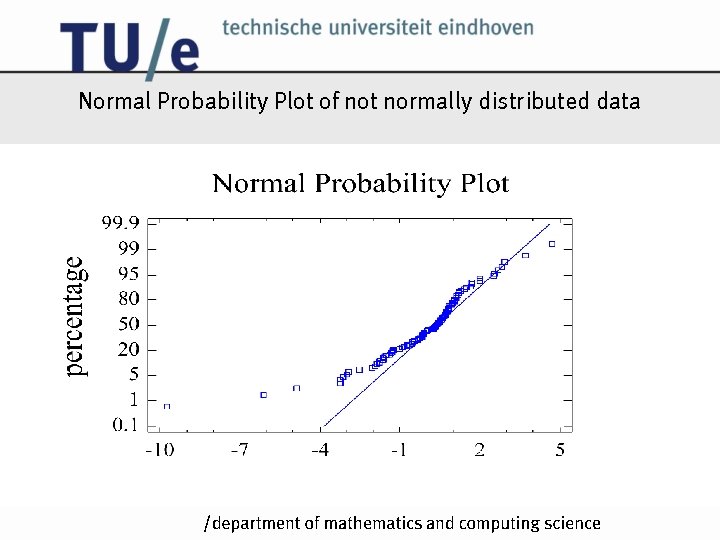
Normal Probability Plot of not normally distributed data /k

Test for Normality: Shapiro-Wilks statistical test for Normality: Shapiro-Wilks idea: sophisticated regression analysis in the spirit of normal probability plot makes Normal Probability Plot objective check outliers (measurement error? ; normality sometimes disturbed by single observation) analyse if not normally distributed Remark: with many observations normality will always be rejected!! /k

Statgraphics: Shapiro-Wilks Describe -> Distributions -> Distribution Fitting (Uncensored Data)… /k

Statgraphics: Shapiro Wilks Tests for Normality for width Computed Chi-Square goodness-of-fit statistic = 254. 667 P-Value = 0. 0 Shapiro-Wilks W statistic = 0. 921395 P-Value = 0. 000722338 Interpretation: • value statistic itself cannot need be interpreted • P-value indicates how likely normal distribution is • use = 0. 01 as critical value in order to avoid too strict rejections of normality /k
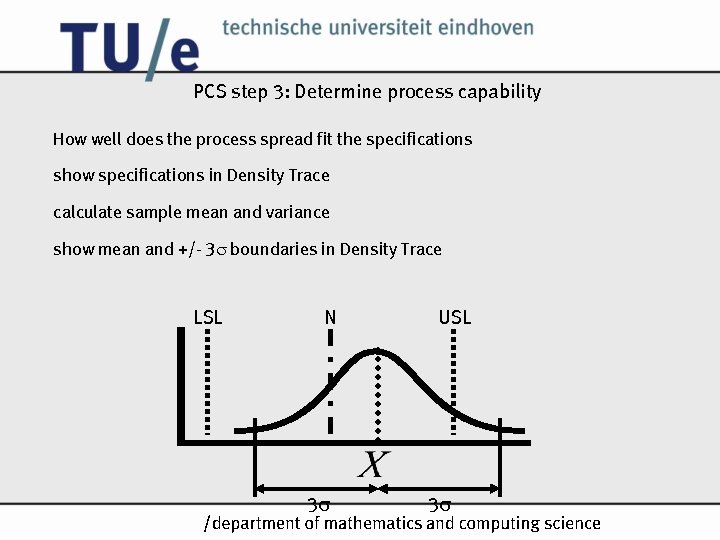
PCS step 3: Determine process capability How well does the process spread fit the specifications show specifications in Density Trace calculate sample mean and variance show mean and +/- 3 boundaries in Density Trace LSL N USL /k 3 3
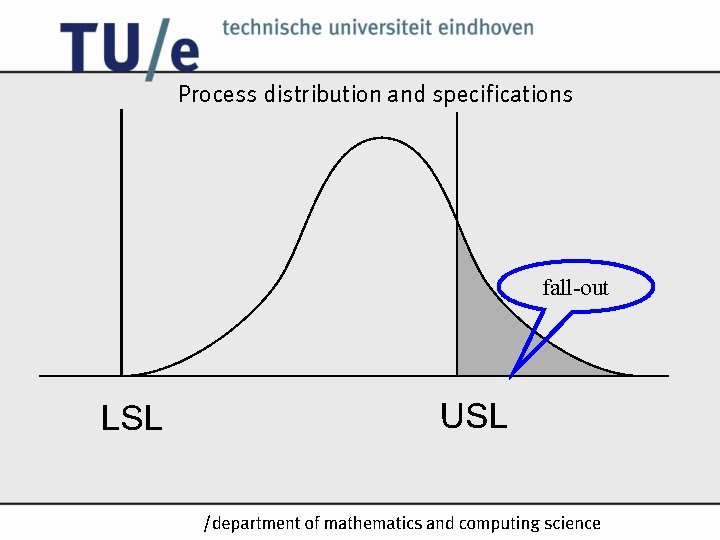
Process distribution and specifications fall-out /k
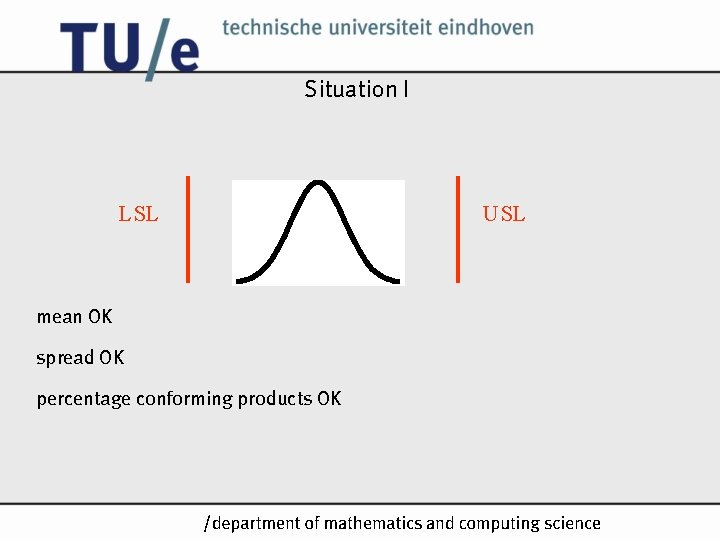
Situation I LSL USL mean OK spread OK percentage conforming products OK /k
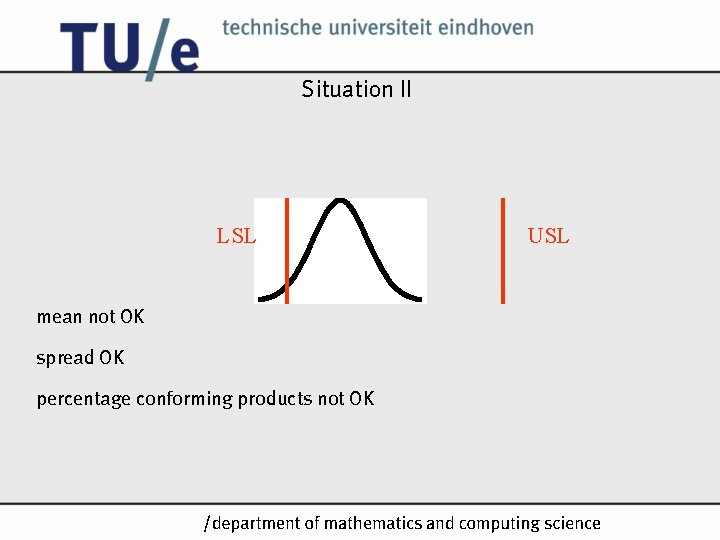
Situation II LSL USL mean not OK spread OK percentage conforming products not OK /k
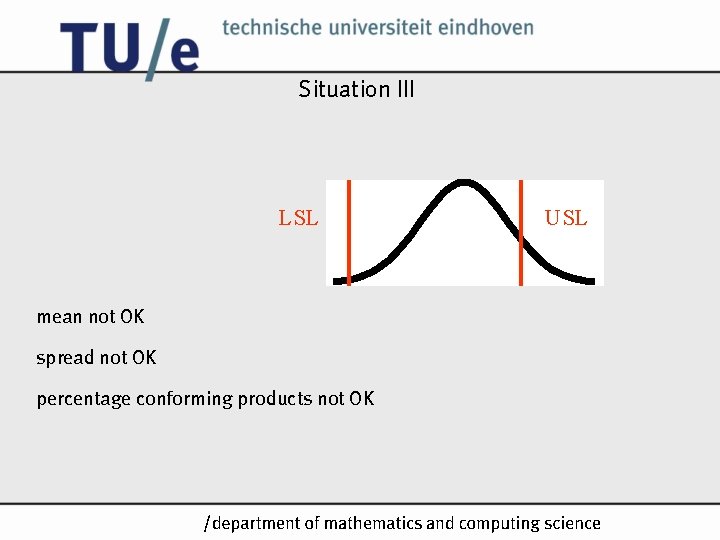
Situation III LSL USL mean not OK spread not OK percentage conforming products not OK /k
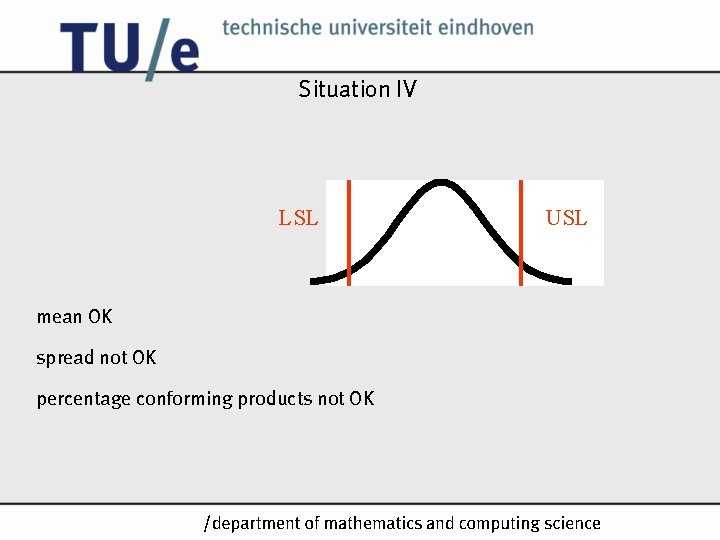
Situation IV LSL USL mean OK spread not OK percentage conforming products not OK /k
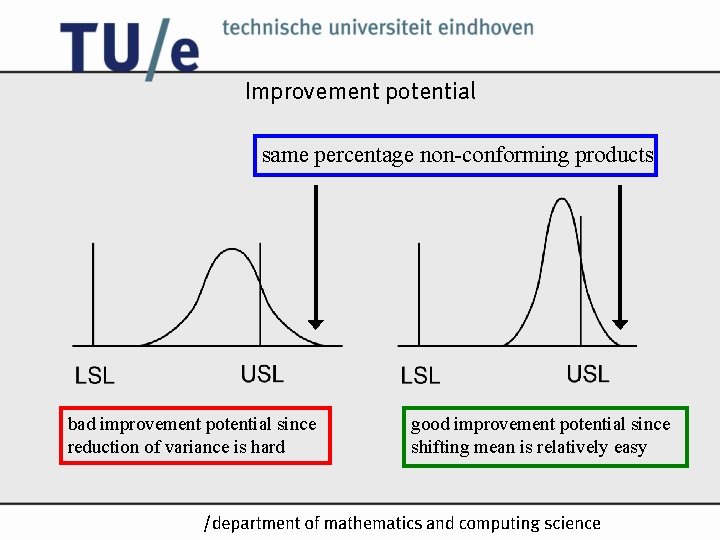
Improvement potential same percentage non-conforming products bad improvement potential since reduction of variance is hard good improvement potential since shifting mean is relatively easy /k

Capability Indices Process Capability Indices are used as metrics to indicate process capability: • Cp (also called PCR or Pp) • Cpk (also called PCRk or Ppk) • Cpm (also called PCRm or Ppm) • . . . Cp must not be confused with Cp from regression analysis. /k
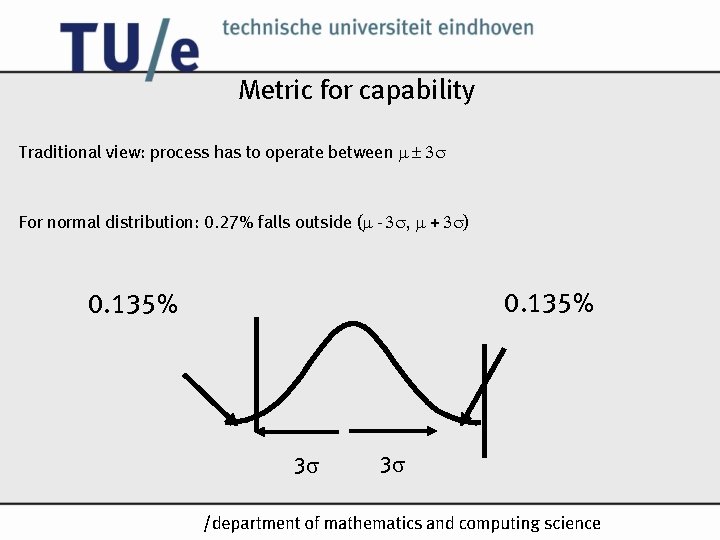
Metric for capability Traditional view: process has to operate between For normal distribution: 0. 27% falls outside ( - , + ) 0. 135% 3 3 /k
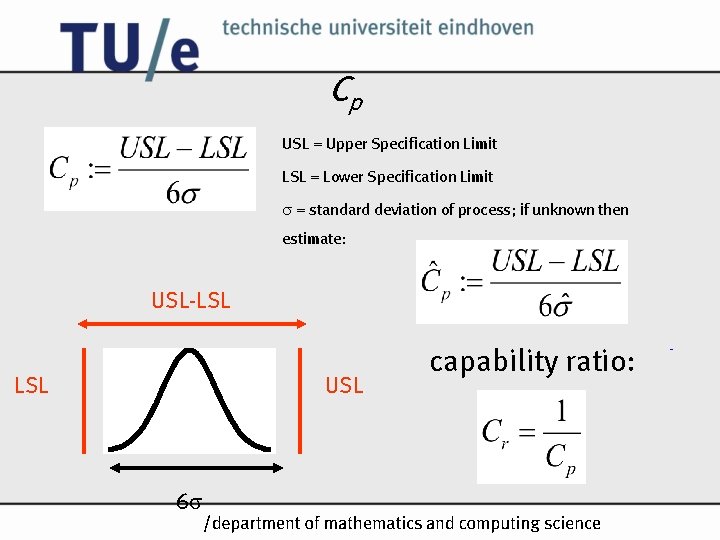
Cp USL = Upper Specification Limit LSL = Lower Specification Limit = standard deviation of process; if unknown then estimate: USL-LSL USL 6 capability ratio: /k
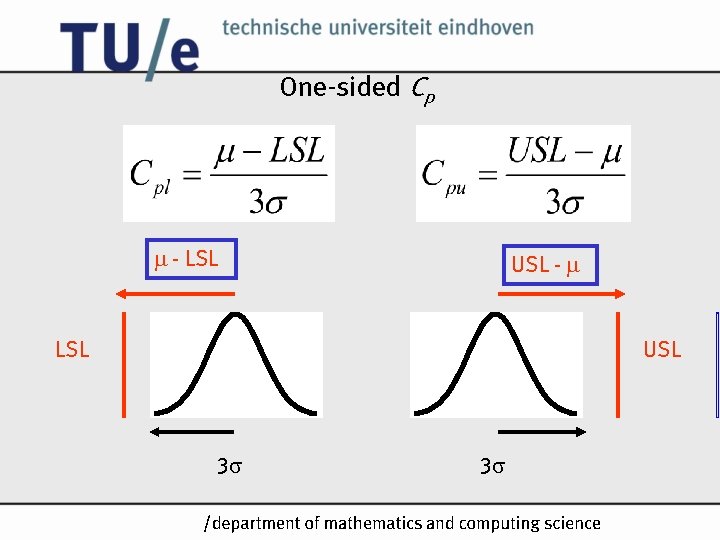
One-sided Cp - LSL USL - LSL USL 3 3 /k
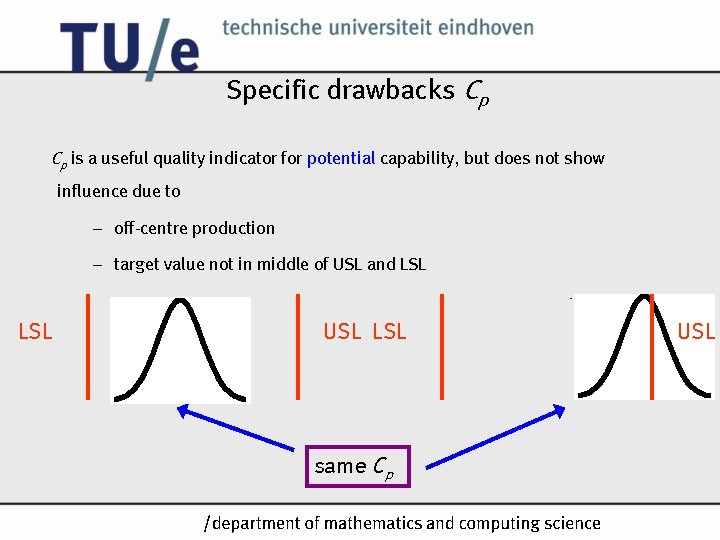
Specific drawbacks Cp Cp is a useful quality indicator for potential capability, but does not show influence due to – off-centre production – target value not in middle of USL and LSL USL LSL same Cp /k USL

Cpk Cpk=min(Cpl, Cpu) Cpk indicates realised capability We always have Cpk Cp (why? ) • if Cpk= Cp, then process is centred at middle value of specifications • if Cpk< Cp, then process is not centred at middle value of specifications /k
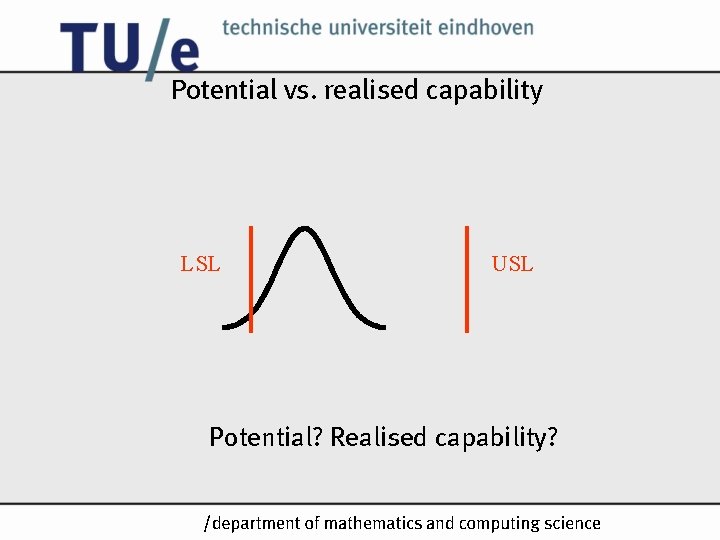
Potential vs. realised capability LSL USL Potential? Realised capability? /k

Specific drawbacks Cpk • cannot be used for one-sided specifications • does not give insight in centring /k
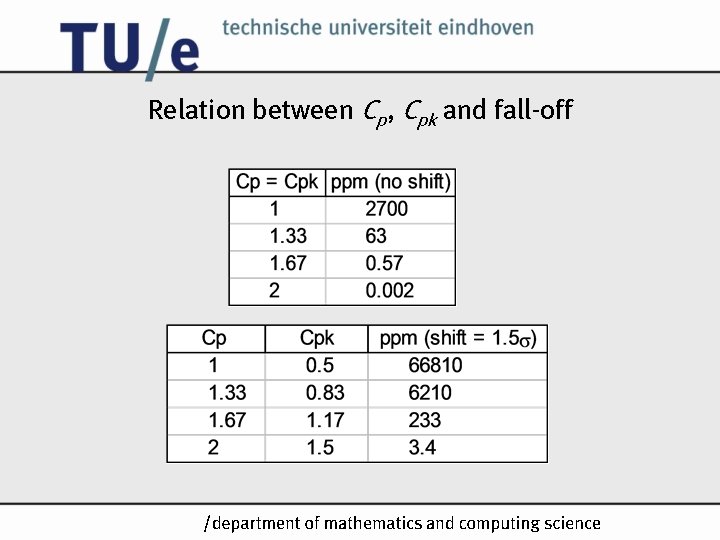
Relation between Cp, Cpk and fall-off /k
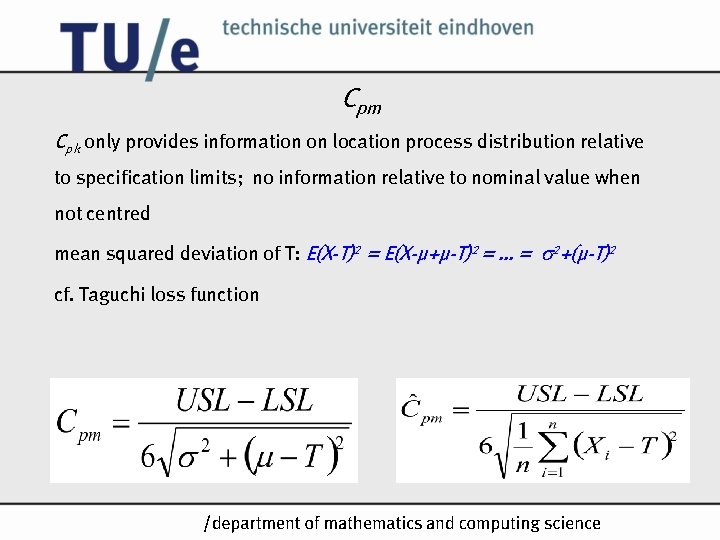
Cpm Cpk only provides information on location process distribution relative to specification limits; no information relative to nominal value when not centred mean squared deviation of T: E(X-T)2 = E(X-µ+µ-T)2 = … = 2+(µ-T)2 cf. Taguchi loss function /k

General drawbacks capability indices • single numbers can only partially describe characteristics of production process • no direct relation with percentage non-conforming products /k

Normality all results given so far assume normally distributed data if data is non-normal, then standard indices maybe misleading normality must be checked by: – normal probability plot (graphical check) – Shapiro-Wilks test (formal test) for non-normal distributions possible solutions are: – transform data – replace 6 in definitions by suitable interquantile distance /k – Pearson family of distributions
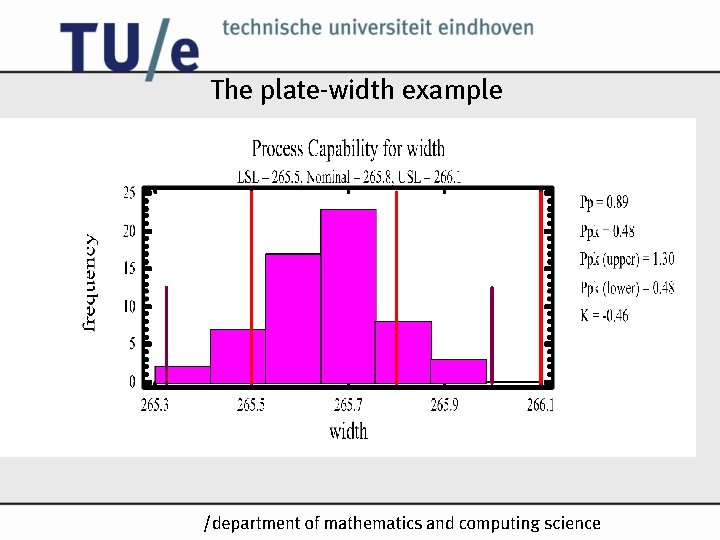
The plate-width example /k
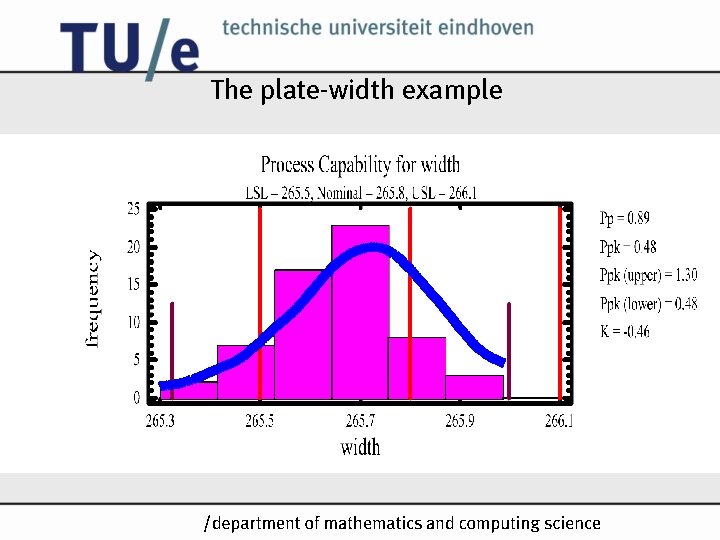
The plate-width example /k

Confidence intervals • process capability indices are merely point estimators • confidence intervals indicate uncertainty in estimates • confidence intervals may also be used for testing • (too) small sample sizes result in (too) wide confidence intervals • mathematical derivation of confidence intervals for capability indices is difficult; many sources (software!) give inaccurate approximations /k
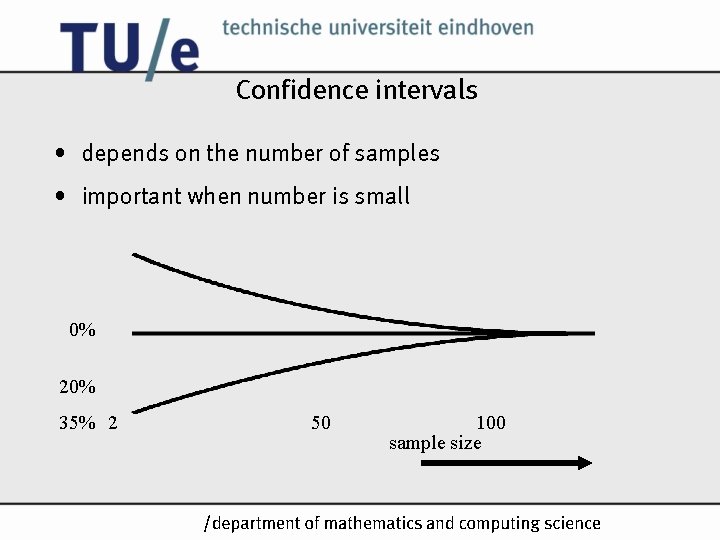
Confidence intervals • depends on the number of samples • important when number is small 0% 20% 35% 2 50 100 sample size /k

Confidence interval for Cp based on normality! /k

Confidence interval for Cpk • based on normality • is good approximation /k

Confidence interval for Cpm where • based on normality • is good approximation /k
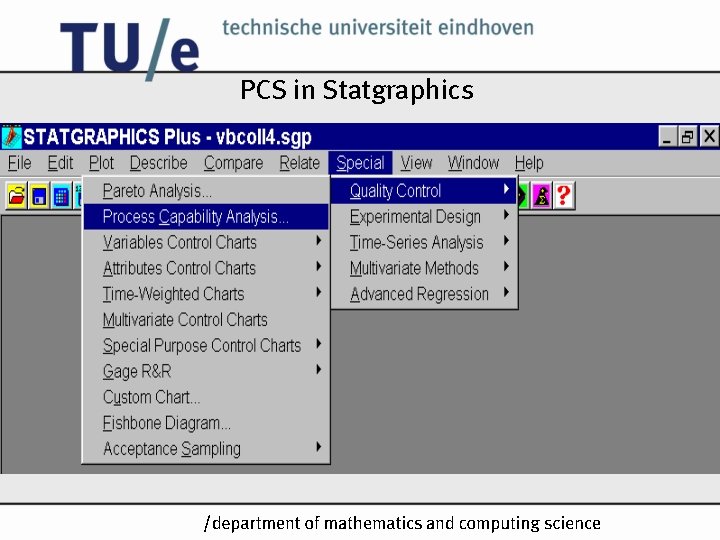
PCS in Statgraphics /k
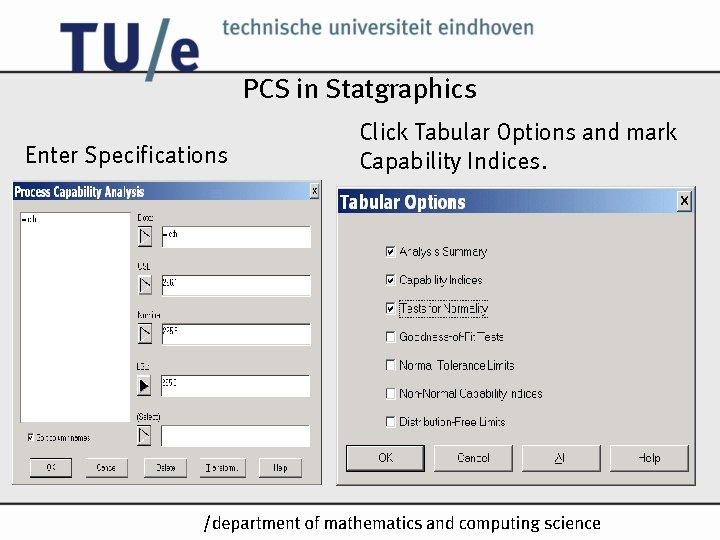
PCS in Statgraphics Enter Specifications Click Tabular Options and mark Capability Indices. /k
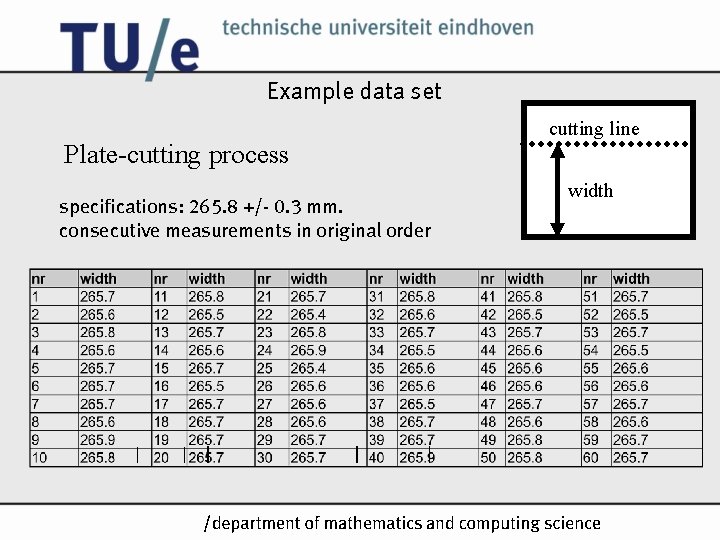
Example data set Plate-cutting process specifications: 265. 8 +/- 0. 3 mm. consecutive measurements in original order cutting line width /k

Process in statistical control? • subgroups of 5 • control limits: • all subgroups inside control limits /k

Pitfalls and frequent faults • data has to be normally distributed • process must be in statistical control • data have to consist of successive individual observations • process capability study is not updated • use indices rather than confidence intervals for indices • link between fall-off and capability indices /k

Standards for Cp and Cpk • 1. 67 is common: this is less than 0. 57 PPM • nowadays more often 2 is used: this is less than 0. 002 PPM • high demands have to be made concerning test production or PCS for one series /k
- Slides: 62