Cap 5 Introduo anlise diferencial de escoamentos 5

Cap. 5 – Introdução à análise diferencial de escoamentos 5. 1 – Conservação da massa 5. 2 – Função corrente 5. 3 – Movimento de um elemento fluido - Cinemática 5. 4 – Equação da Quantidade de Movimento

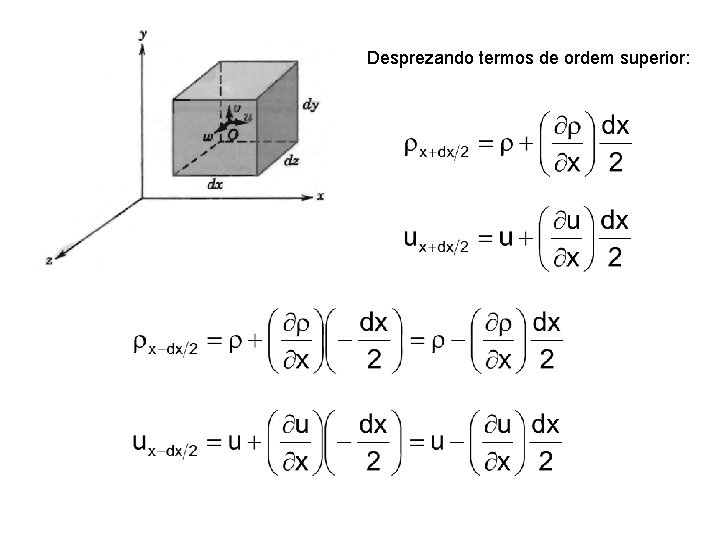
5. 1 – Conservação da massa 5. 1. 1 – Coordenadas retangulares Expansão em série de Taylor :

Desprezando termos de ordem superior:

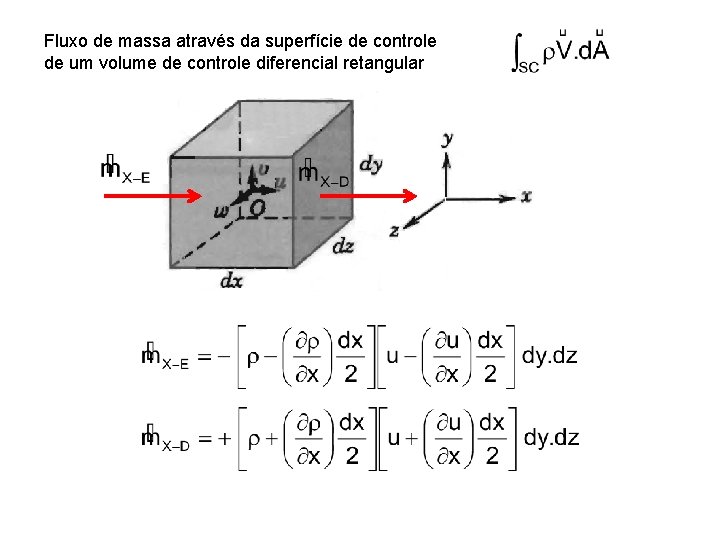
Fluxo de massa através da superfície de controle de um volume de controle diferencial retangular

Fluxo de massa total através da superfície de controle de um volume de controle diferencial retangular

Conservação da massa para um volume de controle diferencial retangular No volume de controle diferencial a massa específica é independente do volume Equação diferencial para o princípio da conservação da massa

Operador GRADIENTE (sobre campo escalar U) Operador DIVERGENTE (sobre campo vetorial A)

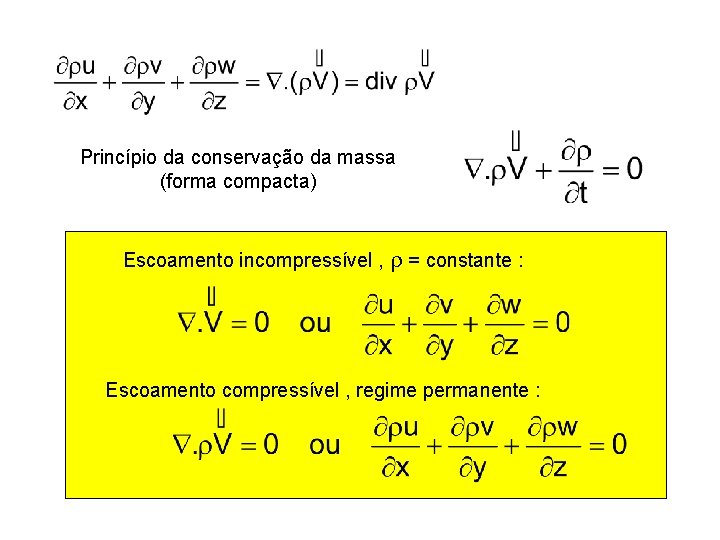
Princípio da conservação da massa (forma compacta) Escoamento incompressível , r = constante : Escoamento compressível , regime permanente :

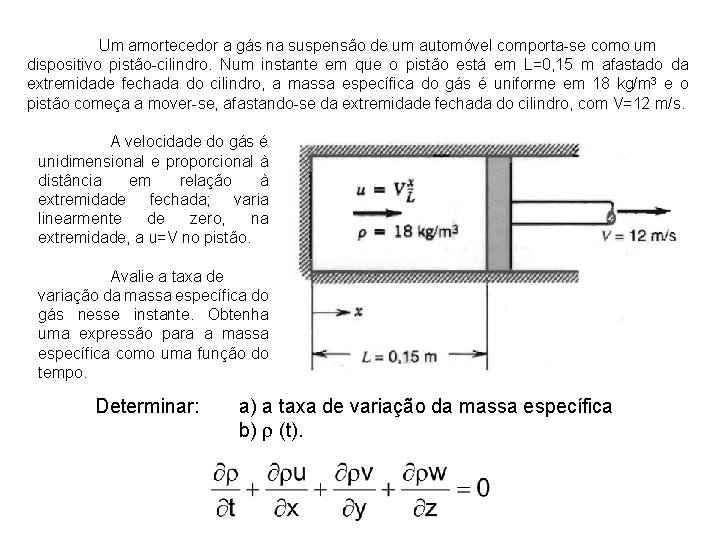
Um amortecedor a gás na suspensão de um automóvel comporta-se como um dispositivo pistão-cilindro. Num instante em que o pistão está em L=0, 15 m afastado da extremidade fechada do cilindro, a massa específica do gás é uniforme em 18 kg/m 3 e o pistão começa a mover-se, afastando-se da extremidade fechada do cilindro, com V=12 m/s. A velocidade do gás é unidimensional e proporcional à distância em relação à extremidade fechada; varia linearmente de zero, na extremidade, a u=V no pistão. Avalie a taxa de variação da massa específica do gás nesse instante. Obtenha uma expressão para a massa específica como uma função do tempo. Determinar: a) a taxa de variação da massa específica b) r (t).

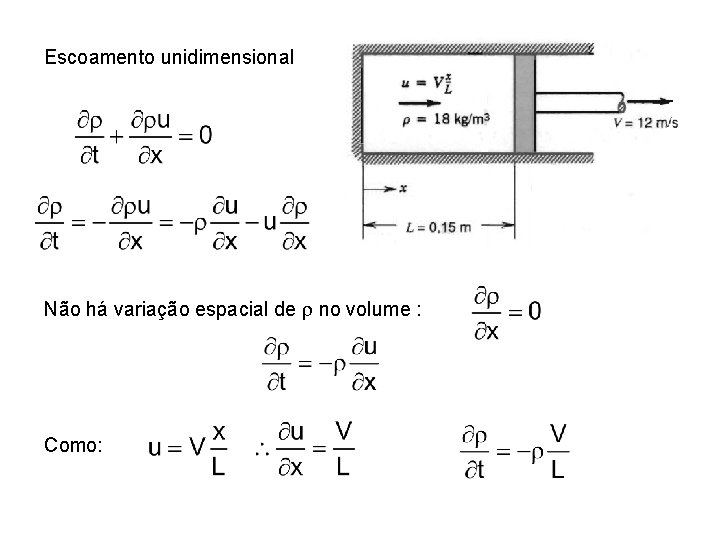
Escoamento unidimensional Não há variação espacial de r no volume : Como:

Com esta derivada obtém a taxa de variação da massa específica no instante inicial (item a): Notando que L é variável no tempo:

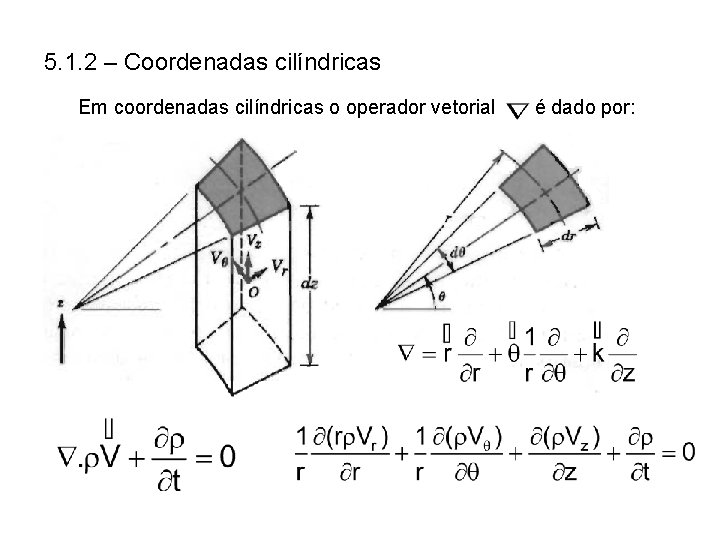
5. 1. 2 – Coordenadas cilíndricas Em coordenadas cilíndricas o operador vetorial é dado por:

Princípio da conservação da massa em coordenadas cilíndricas Escoamento incompressível , r = constante : Escoamento compressível , regime permanente :

5. 2 – Função corrente para escoamento incompressível bidimensional O objetivo é descrever matematicamente várias configurações geométricas de escoamentos bidimensionais: Se uma função contínua, chamada função corrente, for definida de modo que: A função corrente satisfaz a equação da continuidade (eq. da cons. da massa) :

As linhas de corrente são linhas traçadas no campo de escoamento tais que, em um dado instante, são tangentes à direção do escoamento, em cada ponto. Sendo um elemento de comprimento da linha de corrente: Assim, a equação de uma linha de corrente em um escoamento bidimensional é : Substituindo as equações da função corrente, tem-se, para um linha de corrente:

Para uma linha de corrente: Entre dois pontos quaisquer: As linhas de corrente instântaneas Para uma profundidade unitária, a vazão através de AB é: Ao longo de AB, x=constante, e . Portanto:

Em coordenadas cilíndricas : Princípio da Conservação da Massa, escoamento bidimensional: Velocidade radial, tangencial e respectiva função corrente

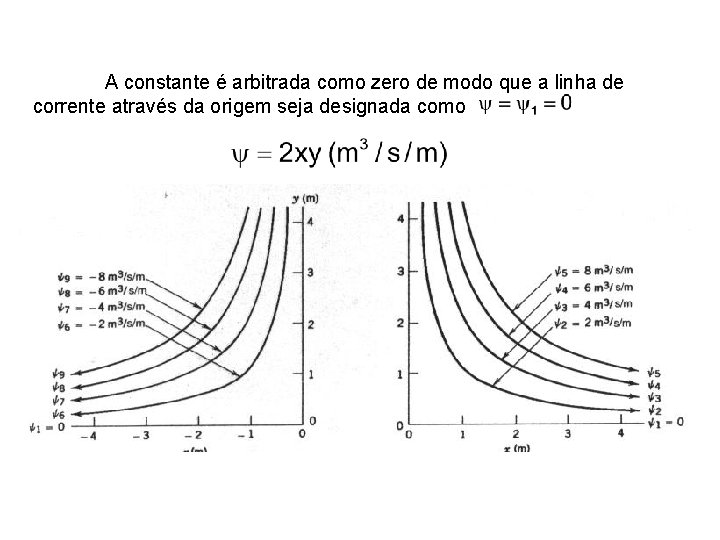
Dados: Campo de velocidade, Determinar: com A = 2 s-1. (a) Função corrente (b) Trace gráficos no primeiro e segundo quadrantes Do campo de velocidade dado : Integrando com relação a y : A função f(x) pode ser avaliada usando-se a equação para v :

A constante é arbitrada como zero de modo que a linha de corrente através da origem seja designada como

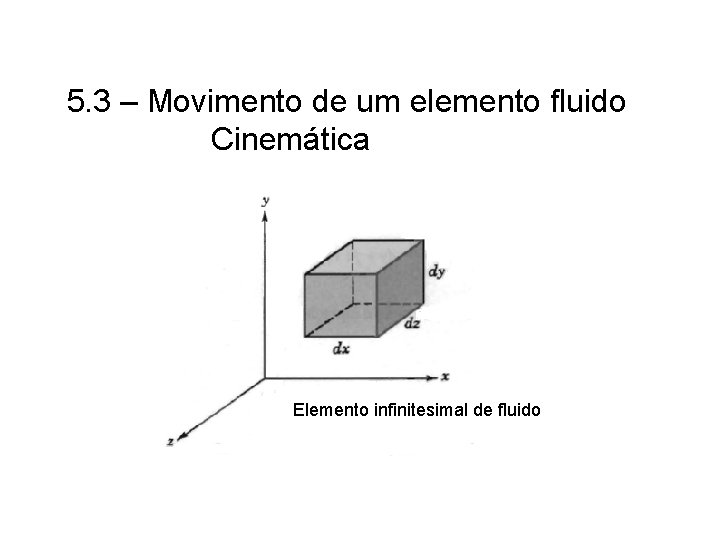
5. 3 – Movimento de um elemento fluido Cinemática Elemento infinitesimal de fluido

5. 3. 1 Aceleração de uma partícula fluida em um campo de velocidade Translação Deformação Angular Rotação Deformação Linear

Dado o campo de velocidade, aceleração de uma partícula fluida, , determine a , a variação da velocidade da partícula, ao mover-se da posição para é dada por:

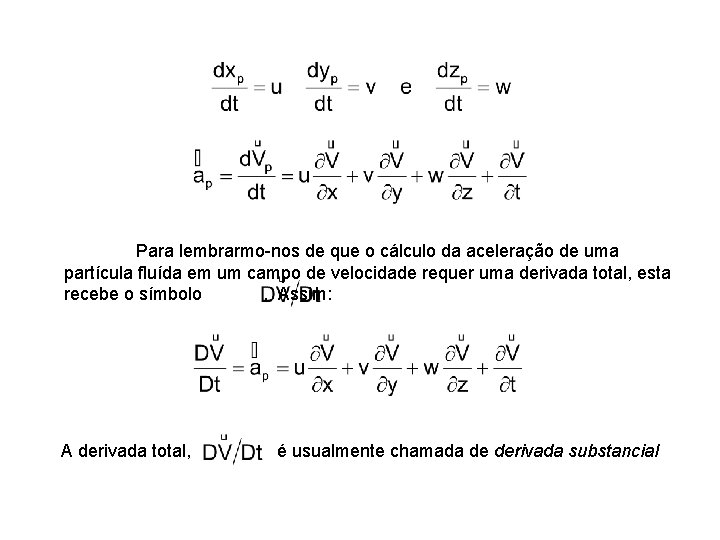
Para lembrarmo-nos de que o cálculo da aceleração de uma partícula fluída em um campo de velocidade requer uma derivada total, esta recebe o símbolo. Assim: A derivada total, é usualmente chamada de derivada substancial

aceleração total de uma partícula Para escoamento bidimensional : aceleração convectiva aceleração local Para escoamento unidimensional :

Em coordenadas retangulares (três componentes da aceleração total): Em coordenadas cilíndricas (três componentes da aceleração total) :

Dados : Escoamento permanente, unidimensional, incompressível, através do duto convergente mostrado. Determinar : (a) A componente x da aceleração de uma partícula movendose no campo de escoamento (b) Para a partícula localizada em x=0 em t=0, obtenha uma expressão para a sua: (1) Posição , xp , como uma função do tempo. (2) Componente x da aceleração, axp. como uma função do tempo.

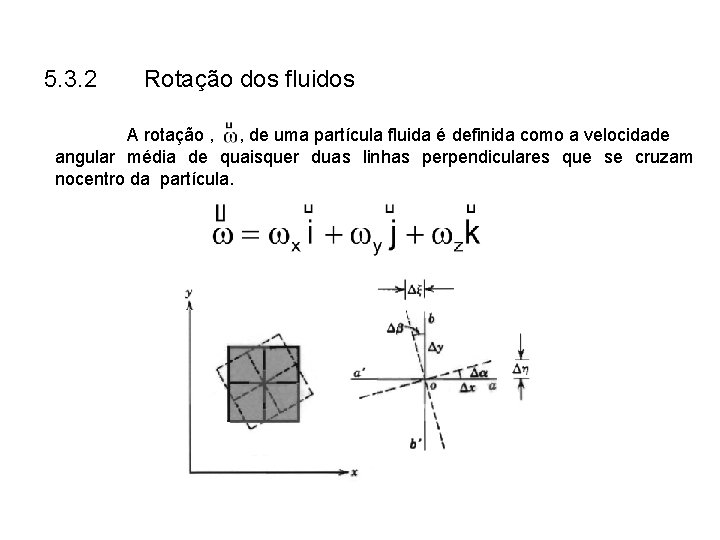
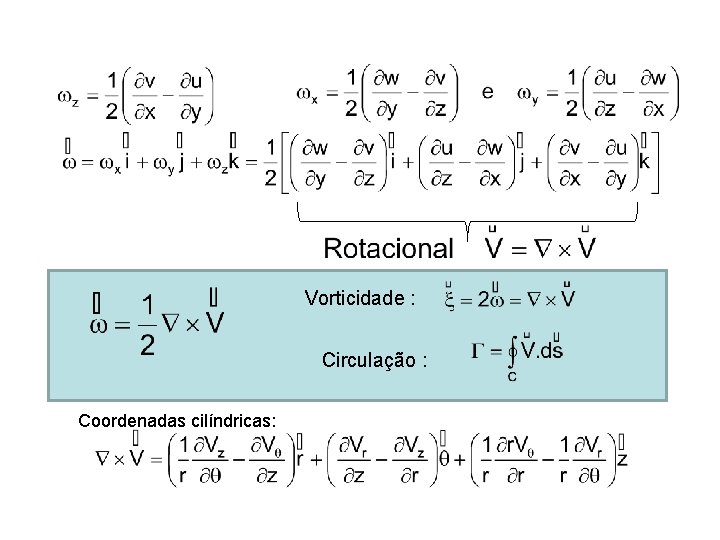
5. 3. 2 Rotação dos fluidos A rotação , , de uma partícula fluida é definida como a velocidade angular média de quaisquer duas linhas perpendiculares que se cruzam nocentro da partícula.

Vorticidade : Circulação : Coordenadas cilíndricas:

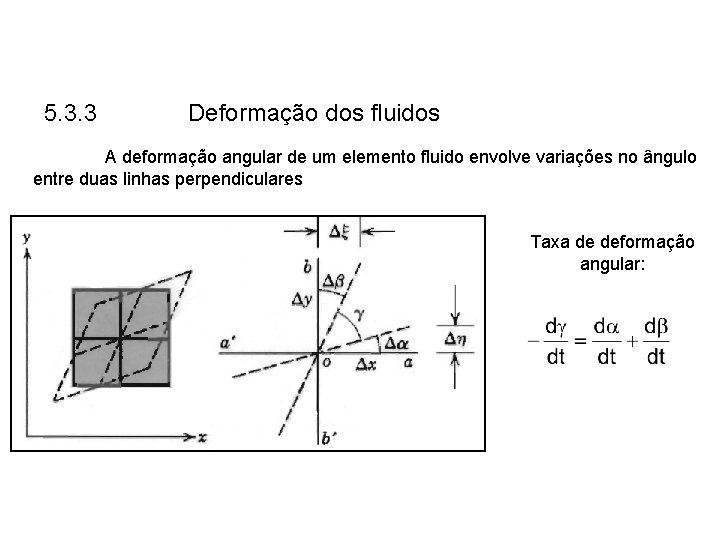
5. 3. 3 Deformação dos fluidos A deformação angular de um elemento fluido envolve variações no ângulo entre duas linhas perpendiculares Taxa de deformação angular:

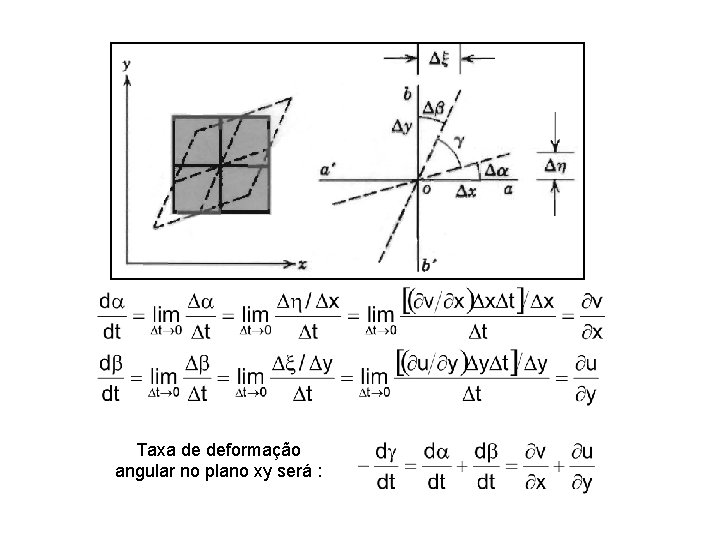
Taxa de deformação angular no plano xy será :

Dados : Campo de velocidade, U= 4 mm/s e h= 4 mm. Partículas fluidas marcadas em t=0 formando uma cruz, como mostrado: Determinar : (a) As posições dos pontos a´, b´, c´ e d´ em t= 1, 5 s. (b) Taxa de deformação angular. (c) Taxa de rotação de uma partícula fluida. A taxa de deformação angular é: A rotação é:

5. 4 – Equação da quantidade de movimento Uma equação dinâmica descrevendo o movimento do fluido pode ser obtida aplicando-se a segunda lei de Newton a uma partícula A quantidade de movimento do sistema é: Para um sistema infinitesimal de massa dm:

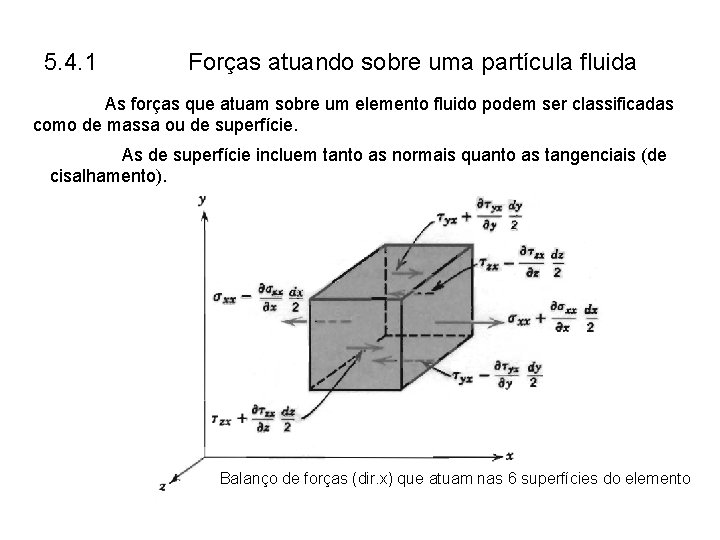
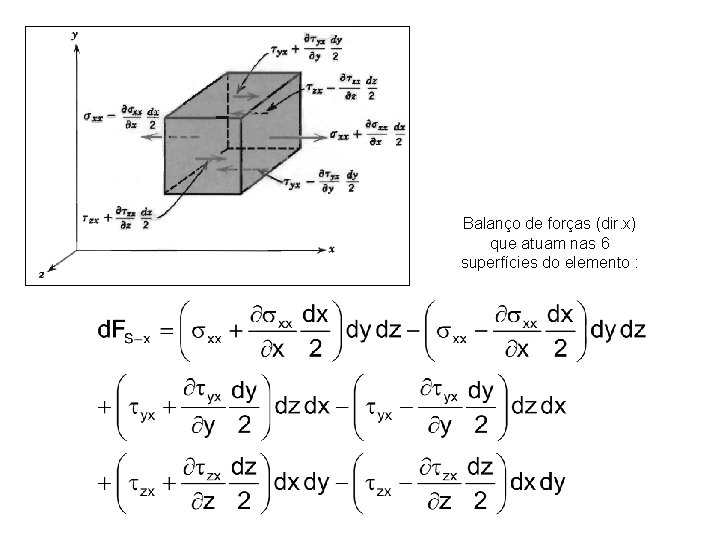
5. 4. 1 Forças atuando sobre uma partícula fluida As forças que atuam sobre um elemento fluido podem ser classificadas como de massa ou de superfície. As de superfície incluem tanto as normais quanto as tangenciais (de cisalhamento). Balanço de forças (dir. x) que atuam nas 6 superfícies do elemento

Balanço de forças (dir. x) que atuam nas 6 superfícies do elemento :

Força infinitesimal resultante de superfície na direção x: Forças infinitesimais resultante (de campo e de superfície) nas direções x, y e z:

5. 4. 2 Equação diferencial da Quantidade de Movimento nas direções x, y e z:

5. 4. 3 Fluidos Newtonianos : a Equação de Navier-Stokes Para um fluido newtoniano, as tensões viscosas são proporcionais às taxas de deformação angular. As tensões podem ser expressas em termos dos gradientes de velocidade e das propriedades dos fluidos (em coordenadas retangulares), como segue (p é a pressão termodinâmica local) : Correlações para tensões superficiais no elemento fluido infinitesimal

Substituindo as correlações para tensões superfíciais na equação diferencial para quantidade de movimento do elemento fluido infinitesimal : Estas equações do movimento fluido são chamadas de equações de Navier-Stokes.

As equações de Navier-Stokes são simplificadas quando aplicadas a escoamento incompressível (r=cte) e fluidos de viscosidade também constante. Para o caso de escoamento sem atrito resumem à equação de Euler: , as equações acima se