Cantors theory of sets Nave theory of sets

Cantor’s theory of sets

Naïve theory of sets (George Cantor) • What is it a set? • A set is a collection of elements, and it is determined just by its elements; a set consisting of elements a, b, c is denoted: {a, b, c} • An element of a set can be again a set, a set may consist of no elements, it may be empty (denoted by ) ! • Examples: , {a, b}, {b, a}, {a, b, a}, {{a, b}}, {a, {b, a}}, {{ }}} • Sets are identical if and only if (iff) they have exactly the same elements (the principle of extensionality) • Notation: x M – „x is an element of M“ • a {a, b}, a {{a, b}}, {a, b} {{a, b}}, {{ }}}, { }}, but: x for any x (i. e. , for no x holds x ). • {a, b} = {b, a} = {a, b, a}, but: {a, b} {{a, b}} {a, {b, a}} Mathematical Logic 2

Set-theoretical operations (create new sets from sets) • Union: A B = {x | x A or x B} read: „The set of all x such that x is an element of A or x is an element of B. “ • {a, b, c} {a, d} = {a, b, c, d} • {odd numbers} {even numbers} = {natural numbers} – denoted Nat • Ui I Ai = {x | x Ai for some i I} • Let Ai = {x | x = 2. i for some i Nat} • Ui Nat Ai = the set of all even numbers Mathematical Logic 3

Set-theoretical operations (create new sets from sets) • Intersection: A B = {x | x A and x B} read: „The set of all x such that x is an element of A and x is an element of B as well. “ • {a, b, c} {a, d} = {a} • {even numbers} {odd numbers} = • i I Ai = {x | x Ai for all i I} • Let Ai = {x | x Nat, x i} • Then i Nat Ai = Mathematical Logic 4

Relations between sets • a set A is a subset of a set B, denoted A B, iff each element of A is also an element of B. • a set A is a proper subset of a set B, denoted A B, iff each element of A is also an element of B but not vice versa. {a} {a, b} {{a, b}} !!! • It holds: A B, iff A B and A B • It holds: A B, iff A B = A • Proofs homework / seminar Mathematical Logic 5

Some other set-theoretical operations • Difference: A B = {x | x A and x B} • {a, b, c} {a, b} = {c} • Complement: Let A M. The complement of A with respect to M is the set A’ = M A • Cartesian product: A B = { a, b | a A, b B} • where a, b je an ordered couple; the ordering is important: a is the first, b is the second element • It holds: a, b = c, d iff a = c, b = d • But: a, b b, a , though {a, b} = {b, a} !!! • generalization: A … A the set of n-tuples, denoted also by An Mathematical Logic 6

Some other set-theoretical operations • Potential set: 2 A = {B | B A}, denoted also by P(A) 2{a, b} = { , {a}, {b}, {a, b}} 2{a, b, c} = { , {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}} How many elements are there in 2 A ? If |A| is the number of elements (cardinality) of a set A, then 2 A has 2|A| elements (hence the notation: 2 A) 2{a, b} {a} = { , { a, a }, { b, a }, { a, a , b, a }} Mathematical Logic 7

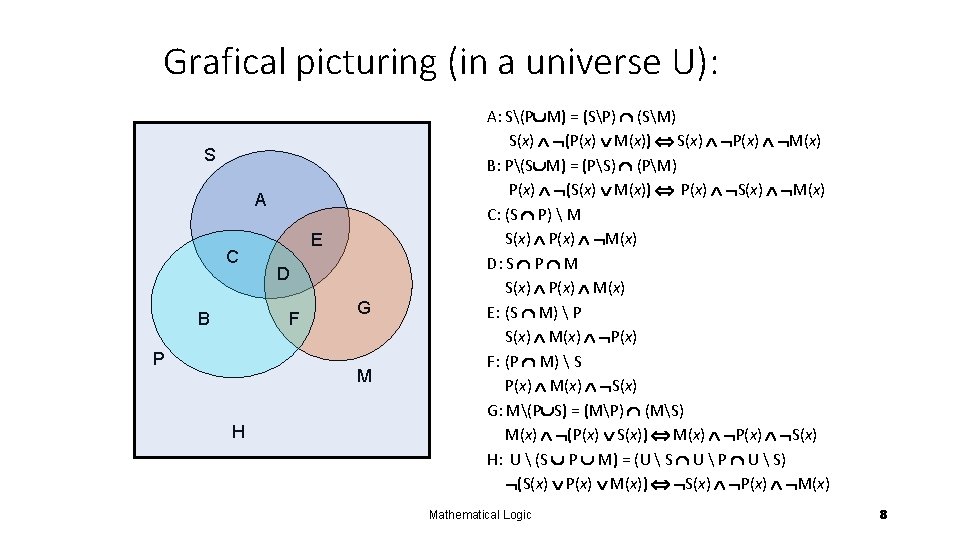
Grafical picturing (in a universe U): S A C B E D F P G M H A: S(P M) = (SP) (SM) S(x) (P(x) M(x)) S(x) P(x) M(x) B: P(S M) = (PS) (PM) P(x) (S(x) M(x)) P(x) S(x) M(x) C: (S P) M S(x) P(x) M(x) D: S P M S(x) P(x) M(x) E: (S M) P S(x) M(x) P(x) F: (P M) S P(x) M(x) S(x) G: M(P S) = (MP) (MS) M(x) (P(x) S(x)) M(x) P(x) S(x) H: U (S P M) = (U S U P U S) (S(x) P(x) M(x)) S(x) P(x) M(x) Mathematical Logic 8

Russell’s paradox • Is it true that any collection of elements (i. e. , the collection defined in an arbitrary way) can be considered to be a set? • It is normal that a set and its elements are entities of different types. Hence a ‘normal set’ is not an element of itself. • Let N be the set of all normal sets: N = {M | M M}. • Question: Is N N ? In other words, is N itself normal or not? • Yes? But then according to the definition of N it holds that N is normal, i. e. , N N. • No? But then N N, hence N is normal, and therefore it belongs to N, i. e. , N N. • Both the answers yield a contradiction; N is not well defined The definition does not determine a collection of elements that could be considered to be a set. Mathematical Logic 9