Canny Edge Detector Detecting Edges in Image l

Detecting Edges in Image l Image I Sobel Edge Detector Threshold Edges

Marr and Hildreth Edge Operator l Smooth by Gaussian l Use Laplacian to find

Marr and Hildreth Edge Operator Zero Crossings Detection Zero Crossings Edge Image

Quality of an Edge Detector l l l Robustness to Noise Localization Too Many/Too

Canny Edge Detector l Criterion 1: Good Detection: The optimal detector must minimize the

Canny Edge Detector l l l Convolution with derivative of Gaussian Non-maximum Suppression Hysteresis

Canny Edge Detector l Smooth by Gaussian l Compute x and y derivatives l

Non-Maximum Suppression We wish to mark points along the curve where the magnitude is

Non-Maximum Suppression l Suppress the pixels in ‘Gradient Magnitude Image’ which are not local

Hysteresis Thresholding l l l If the gradient at a pixel is above ‘High’,

Slides: 23

Download presentation

Canny Edge Detector

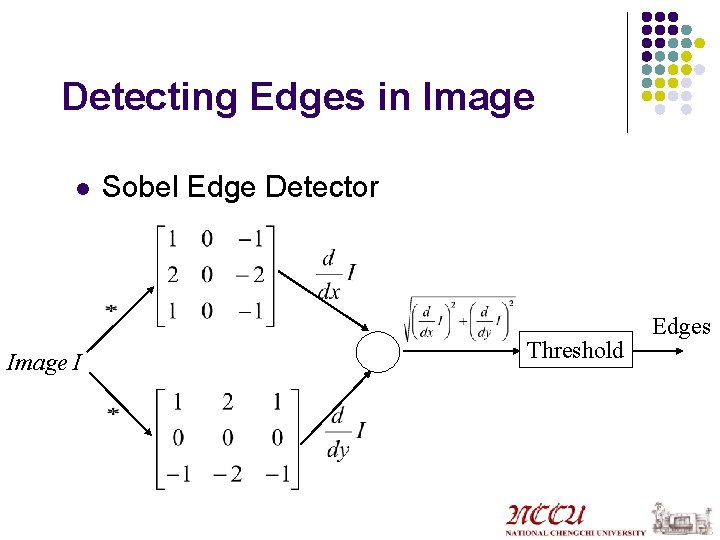
Detecting Edges in Image l Image I Sobel Edge Detector Threshold Edges

Sobel Edge Detector

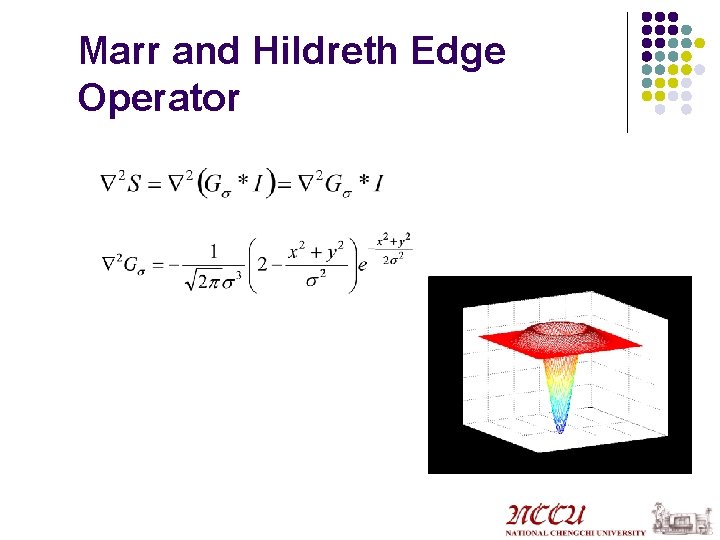
Marr and Hildreth Edge Operator l Smooth by Gaussian l Use Laplacian to find derivatives

Marr and Hildreth Edge Operator

Marr and Hildreth Edge Operator Y X

Marr and Hildreth Edge Operator Zero Crossings Detection Zero Crossings Edge Image

Quality of an Edge Detector l l l Robustness to Noise Localization Too Many/Too less Responses Poor robustness to noise Poor localization True Edge Too many responses

Canny Edge Detector l Criterion 1: Good Detection: The optimal detector must minimize the probability of false positives as well as false negatives. l Criterion 2: Good Localization: The edges detected must be as close as possible to the true edges. l Single Response Constraint: The detector must return one point only for each edge point.

Canny Edge Detector l l l Convolution with derivative of Gaussian Non-maximum Suppression Hysteresis Thresholding

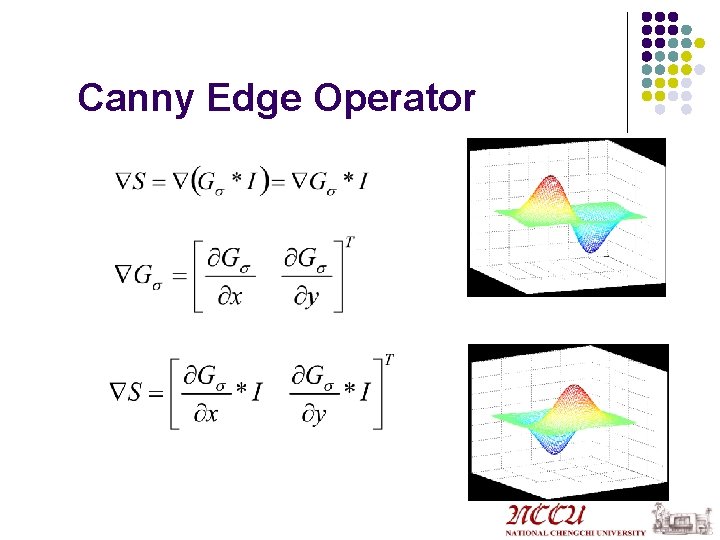
Canny Edge Detector l Smooth by Gaussian l Compute x and y derivatives l Compute gradient magnitude and orientation

Canny Edge Operator

Canny Edge Detector

Non-Maximum Suppression We wish to mark points along the curve where the magnitude is biggest. We can do this by looking for a maximum along a slice normal to the curve (non-maximum suppression). These points should form a curve. There are then two algorithmic issues: at which point is the maximum, and where is the next one?

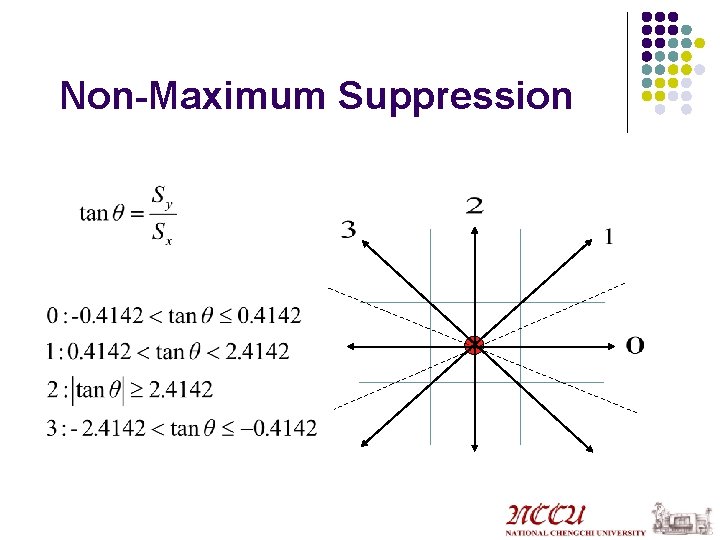
Non-Maximum Suppression l Suppress the pixels in ‘Gradient Magnitude Image’ which are not local maximum

Non-Maximum Suppression

Hysteresis Thresholding

Hysteresis Thresholding l l l If the gradient at a pixel is above ‘High’, declare it an ‘edge pixel’ If the gradient at a pixel is below ‘Low’, declare it a ‘non-edge-pixel’ If the gradient at a pixel is between ‘Low’ and ‘High’ then declare it an ‘edge pixel’ if and only if it is connected to an ‘edge pixel’ directly or via pixels between ‘Low’ and ‘ High’

Hysteresis Thresholding