can be compressed exert pressure on whatever surrounds

• can be compressed • exert pressure on whatever surrounds them • expand into whatever volume is available • easily diffuse into one another • can be described in terms of temperature, pressure, volume and amount

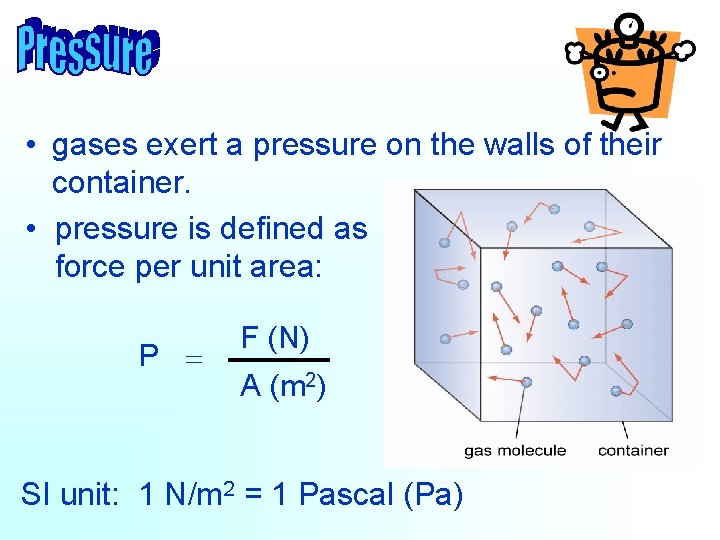
• gases exert a pressure on the walls of their container. • pressure is defined as force per unit area: P = F (N) A (m 2) SI unit: 1 N/m 2 = 1 Pascal (Pa)

The atmospheric pressure can be measured using a barometer.

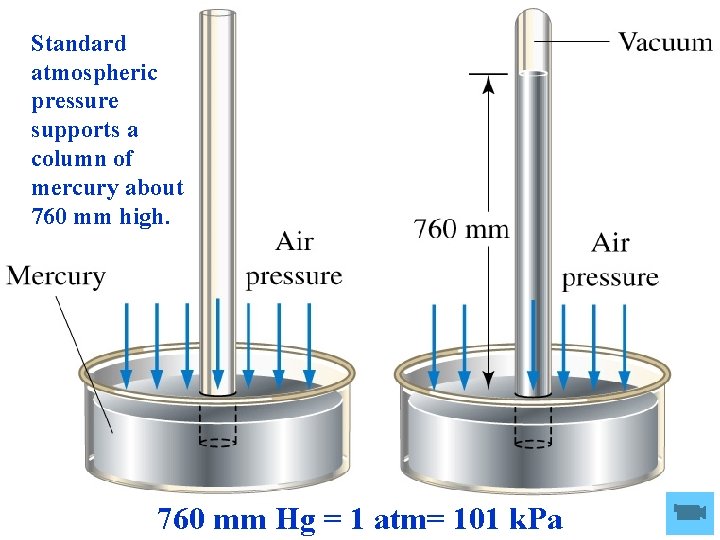
Standard atmospheric pressure supports a column of mercury about 760 mm high. 760 mm Hg = 1 atm= 101 k. Pa

If the barometer reads 753. 3 mm Hg, what is the atmospheric pressure in atm and k. Pa? 753. 3 mm Hg 1 atm 760 mm Hg 101 k. Pa 760 mm Hg = 0. 9912 atm = 100. 1 k. Pa

• Lord Kelvin proposed an absolute temperature scale defined by: T(K) = T(C) + 273. 15

Convert the following temperatures into Kelvin or celcius: 45 o. C → 318. 15 K 207 o. C → 480. 15 K -48 o. C → 225. 15 K 100 K → -173. 15 o. C

Pressure Conversions: 1. 0. 875 atm to mm. Hg 2. 745. 0 mm. Hg to atm 3. 0. 955 atm to k. Pa 4. 98. 35 k. Pa to atm 5. 740. 0 mm. Hg to k. Pa 6. 99. 25 k. Pa to mm. Hg 665 mm Hg 0. 9803 atm 96. 5 k. Pa 0. 9738 atm 98. 34 k. Pa 746. 8 mm Hg

• In order to compare two gases, we choose a standard temperature and pressure: STP: standard temperature and pressure → 273. 15 K and 101. 325 (data booklet) → one mole of gas has a volume of 22. 4 L SATP: standard ambient temperature and pressure → 298. 15 K and 100. 00 k. Pa → one mole of gas has a volume of 24. 8 L

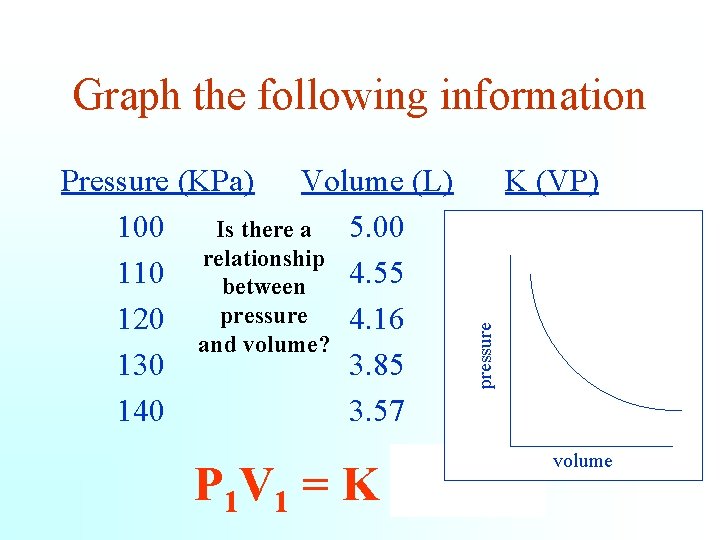
Pressure (KPa) Volume (L) 100 5. 00 Is there a relationship 110 4. 55 between pressure 120 4. 16 and volume? 130 3. 85 140 3. 57 pressure Graph the following information K (VP) 500. 5 499. 2 500. 5 499. 8 P 1 V 1 = K = P 2 V 2 volume

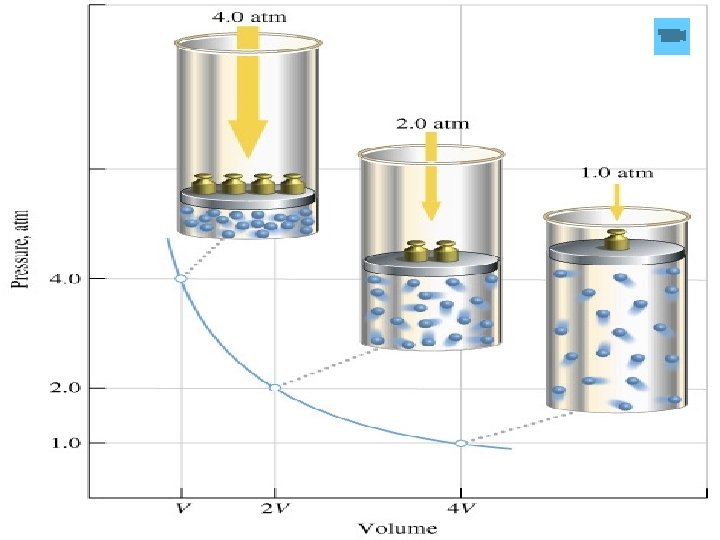
For a given mass of gas at constant temperature, the volume of a gas varies inversely with pressure. P 1 V 1 = P 2 V 2

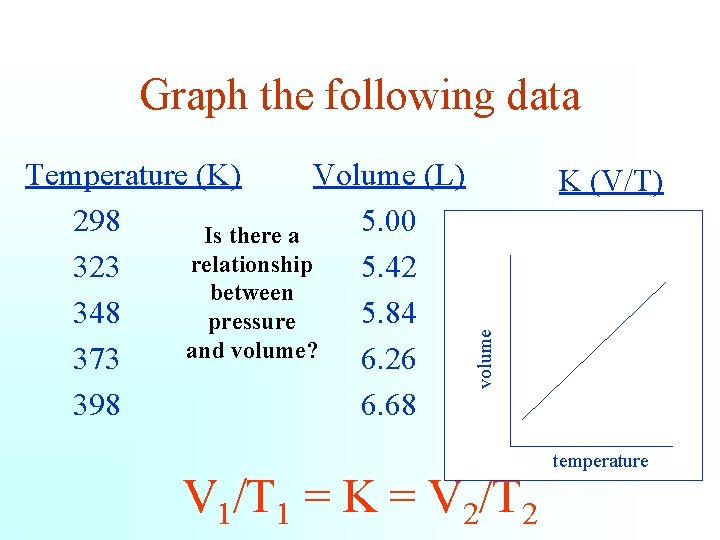
Graph the following data K (V/T) volume Temperature (K) Volume (L) 298 5. 00 Is there a relationship 323 5. 42 between 348 5. 84 pressure and volume? 373 6. 26 398 6. 68 V 1/T 1 = K = V 2/T 2 0. 0167 0. 0168 temperature

Charles discovered that volume is directly proportional to its Kelvin temperature if a fixed mass remains under constant pressure. V 1 V 2 = T 1 T 2

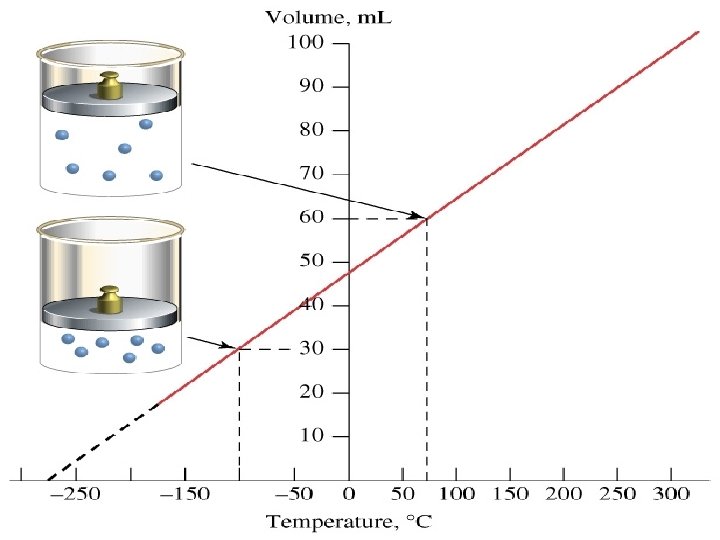
V versus T for different gases

P 1 = T 1 • The pressure of a gas is directly proportional to the Kelvin temperature, providing the volume and mass remain constant. P 2 T 2 Joseph Louis Gay-Lussac and Jean-Baptistse Biot in their balloon on 24 August 1804

V 1 P 1 T 1 = V 2 P 2 T 2

• In 1811, Avogadro proposed that equal volumes of gases at the same temperature and pressure contain equal numbers of molecules. • It follows that the volume of a gas at constant temperature and pressure is proportional to number of moles. V 1 V 2 = n 1 n 2

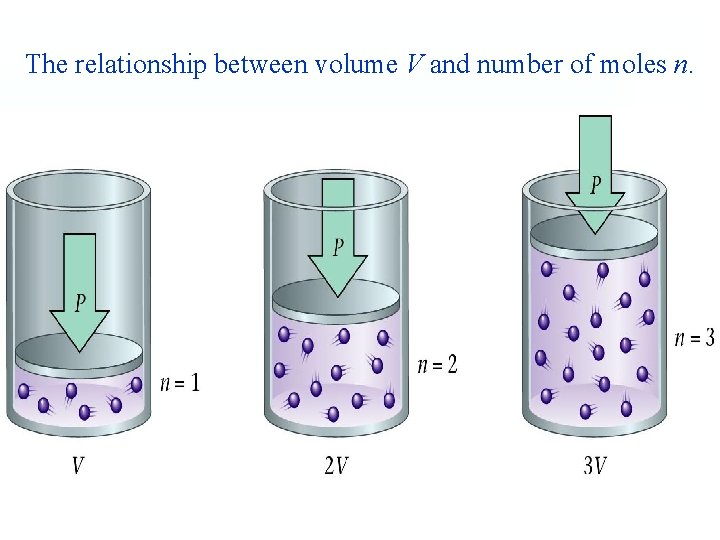
The relationship between volume V and number of moles n.

The Ideal Gas Equation Combining the gas laws gives: PV = n. RT where R is called the Gas constant: × L atm R = 0. 08206 mol × K

• In order to compare two gases, we choose a standard temperature and pressure: STP: 0°C and 1 atm • What is the volume of a mole of gas at STP? = 1 mol = 22. 4 L × 273. 15 K 1 atm

• If 6. 45 grams of water are decomposed, how many liters of oxygen will be produced at STP? 2 H 2 O(g) ® 2 H 2(g) + O 2(g) 6. 45 g H 2 O 1 mol O 2 22. 4 L O 2 18. 02 g H 2 O 2 mol H 2 O 1 mol O 2

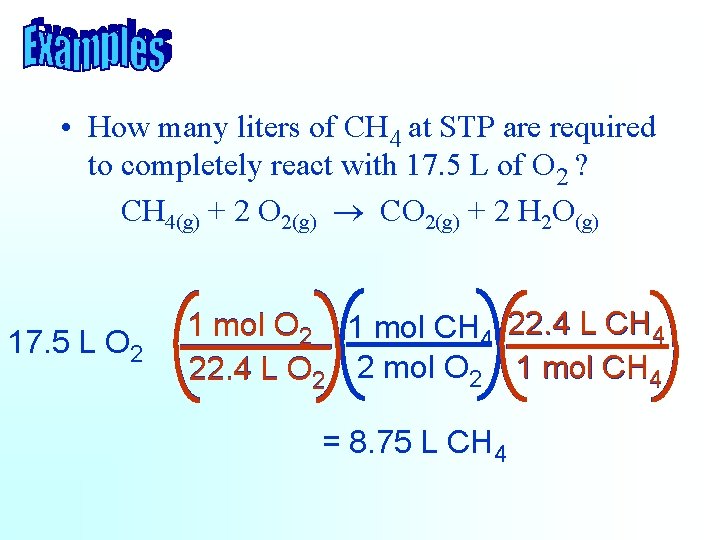
• How many liters of CH 4 at STP are required to completely react with 17. 5 L of O 2 ? CH 4(g) + 2 O 2(g) ® CO 2(g) + 2 H 2 O(g) 17. 5 L O 2 1 mol CH 4 22. 4 L O 2 2 mol O 2 1 mol CH 4 = 8. 75 L CH 4

• Equal volumes of gas, at the same temperature and pressure contain the same number of particles. • Moles are numbers of particles • You can treat reactions as if they happen liters at a time, as long as you keep the temperature and pressure the same.

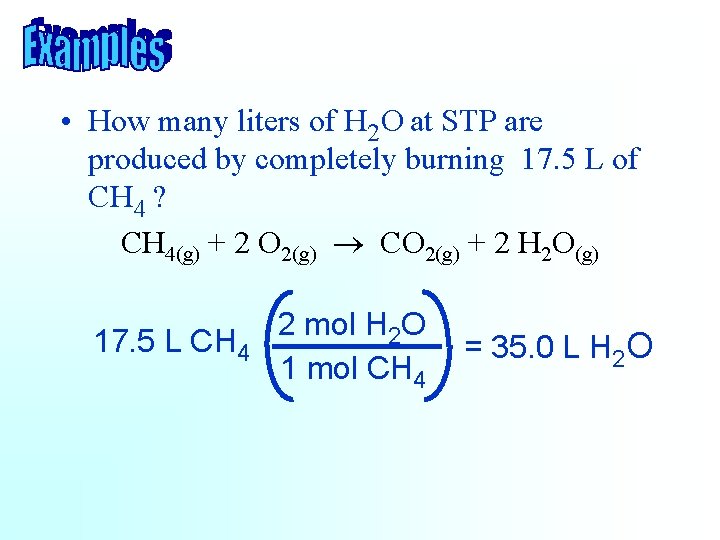
• How many liters of H 2 O at STP are produced by completely burning 17. 5 L of CH 4 ? CH 4(g) + 2 O 2(g) ® CO 2(g) + 2 H 2 O(g) 17. 5 L CH 4 2 mol H 2 O 1 mol CH 4 = 35. 0 L H 2 O

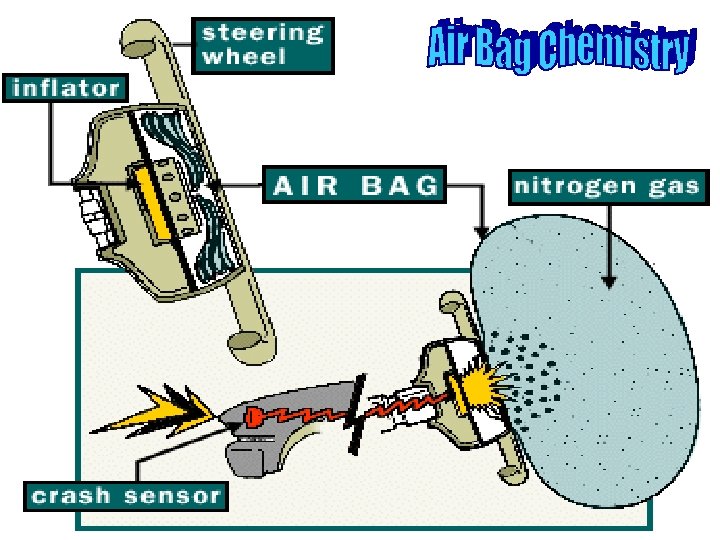
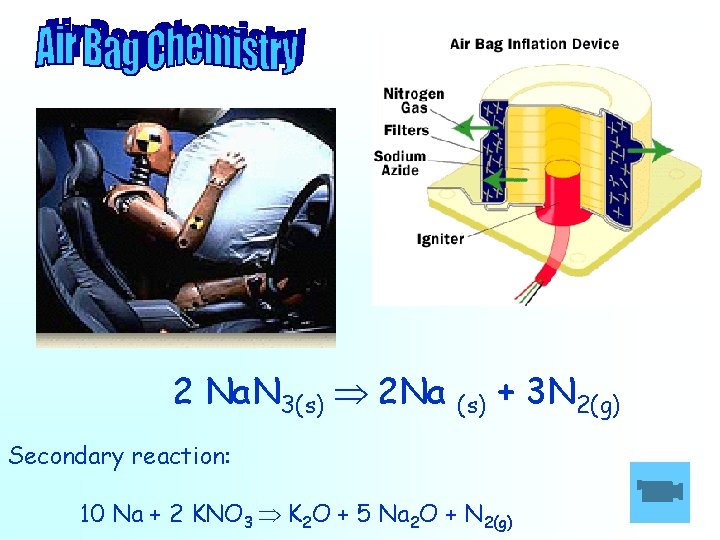
2 Na. N 3(s) 2 Na (s) + 3 N 2(g) Secondary reaction: 10 Na + 2 KNO 3 K 2 O + 5 Na 2 O + N 2(g)

To measure the amount of gas produced in a reaction, it is often collected over water. Mg. O(s) ® Mg(s) + O 2(g)