Camera Model Camera Modeling o Referring figure below

Camera Model

Camera Modeling: o Referring figure below, a world coordinate system (X, Y, Z) is used to locate both the camera and 3 Dpoints (w) on to the image plane. o Camera coordinate system is denoted by (x, y, z) and image points by c.

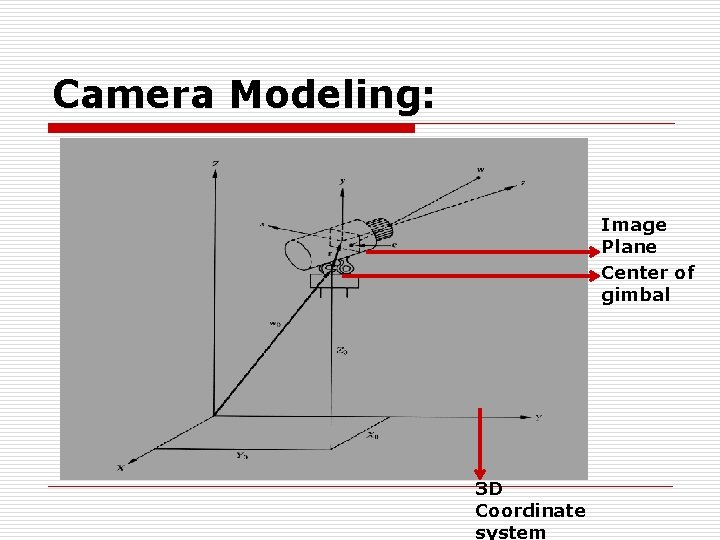
Camera Modeling: Image Plane Center of gimbal 3 D Coordinate system

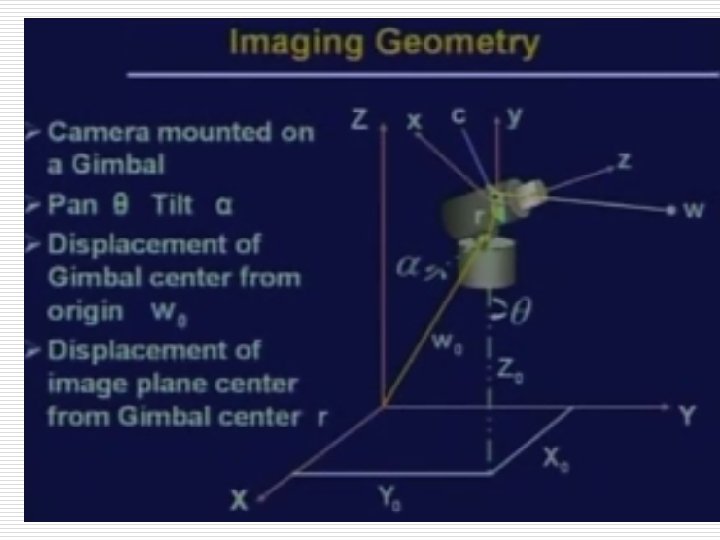
Camera Modeling: o The camera is mounted on the gimbal which allows: n n A pan (angle between x and X axis) of o A tilt (angle between z and Z axis) of 0 o The offset of the center of the gimbal from origin of the world coordinate system is denoted by wo having components (Xo, Yo, Z o) o The offset of the center of the imaging plane w. r. t gimbal center is denoted by r having components (r 1 , r 2 , r 3 ).

Camera Modeling: o Before applying perspective transformation, the camera and world coordinate system must be aligned, and they must be co-incident. o Suppose that initially the camera was in normal position having gimbal center and origin of the image plane at the origin of the world coordinate system.

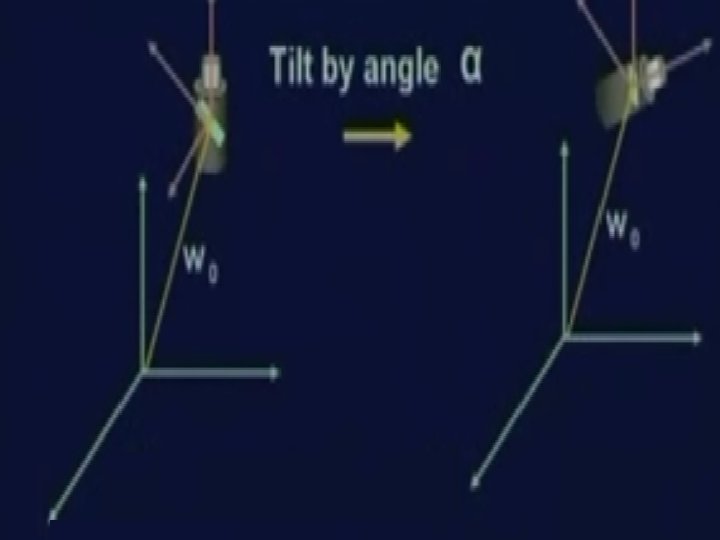
Camera Modeling: o The position shown in figure can be achieved in different ways. Assuming the following steps: 1. Displacement of the gimbal center from the origin. 2. Tilt of the z-axis, 3. Pan of the x-axis, And finally 4. Displacement of the image plane w. r. t. gimbal center.

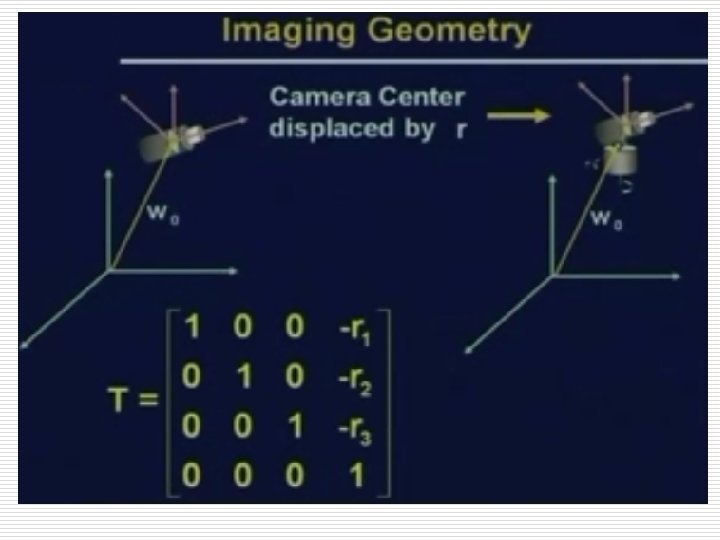
Camera Modeling: 1. G Displacement of the gimbal center from the origin. 1 0 0 0 0 1 0 -xo -yo -zo 1 Translation of the origin of the world coordinate system to the location of the gimbal center can be acomplished by above transformation matrix.

Camera Modeling: 2. R θ Z Tilt of the z-axis, cos sin 0 0 -sin cos 0 0 0 0 1 Tilt (Rotation along Z axis) can be applied by using the above transformation matrix.

Camera Modeling: 3. R α X Pan of the x-axis, 1 0 0 cos sin 0 0 0 -sin 0 cos 0 0 1 Pan (Rotation along X axis) can be applied by using the above transformation matrix.

Camera Modeling: 4. C Displacement of the image plane w. r. t. gimbal center. 1 0 0 0 0 1 0 -r 1 -r 2 -r 3 1 Translation from the gimbal center to the center of Image plane can be accomplished by above transformation matrix.

Camera Modeling: n Applying exactly the same sequence of steps to all world points can achieved the position after which the perspective transformation can be applied.

Camera Modeling: n The series of transformations CRGWh brings the world and camera coordinates system into coincidence. Z X [C (R )GWh ] α θ n Now the Image plane coordinate of a point Wh, can be obtained by applying perspective transformation i. e. Ch = X P[C (Rα)(R Z θ )GWh ]

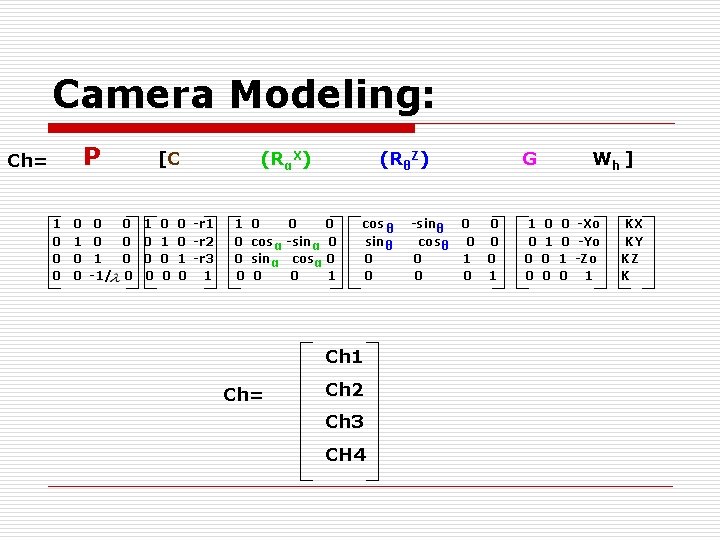
Camera Modeling: P Ch= 1 0 0 0 [C 0 0 0 1 0 0 -r 1 1 0 0 0 1 0 -r 2 0 1 0 0 0 1 -r 3 0 -1/ 0 0 1 (RαX) 1 0 0 cos α sin α 0 (RθZ) 0 0 -sinα 0 cosα 0 0 1 cos θ sinθ 0 0 Ch 1 Ch= Ch 2 Ch 3 CH 4 -sinθ 0 cosθ 0 0 1 0 0 G 0 0 0 1 1 0 0 0 Wh ] 0 1 0 0 0 -Xo 0 -Yo 1 -Zo 0 1 KX KY KZ K

Camera Modeling: n On expanding and solving Cartesian Co-Ordinates X=ch 1/ch 4 y=ch 2/ch 4