Camera calibration Digital Visual Effects YungYu Chuang with

Camera calibration Digital Visual Effects Yung-Yu Chuang with slides by Richard Szeliski, Steve Seitz, , Fred Pighin and Marc Pollefyes

Outline • • • Camera projection models Camera calibration Nonlinear least square methods A camera calibration tool Applications

Camera projection models
Pinhole camera
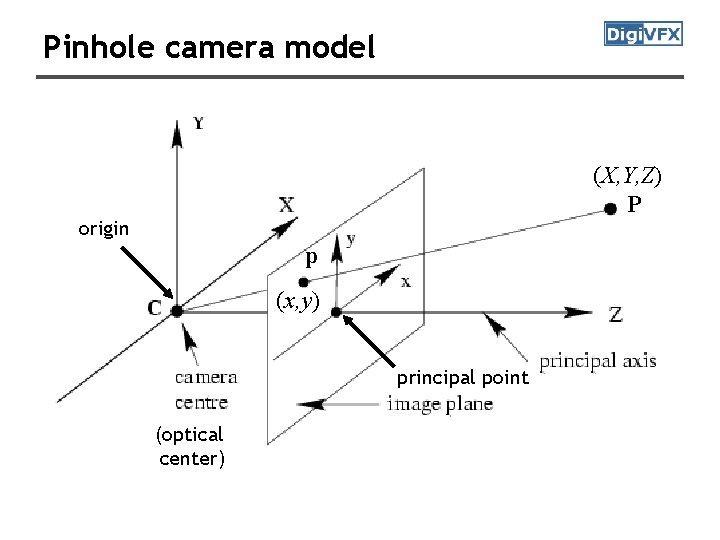
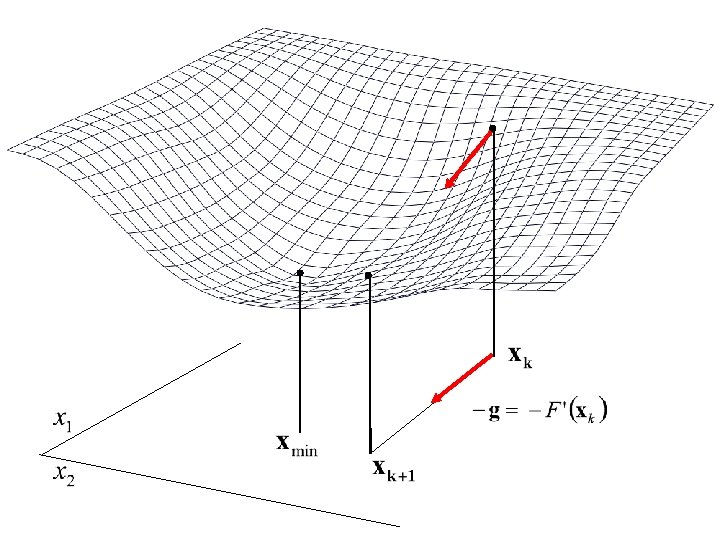
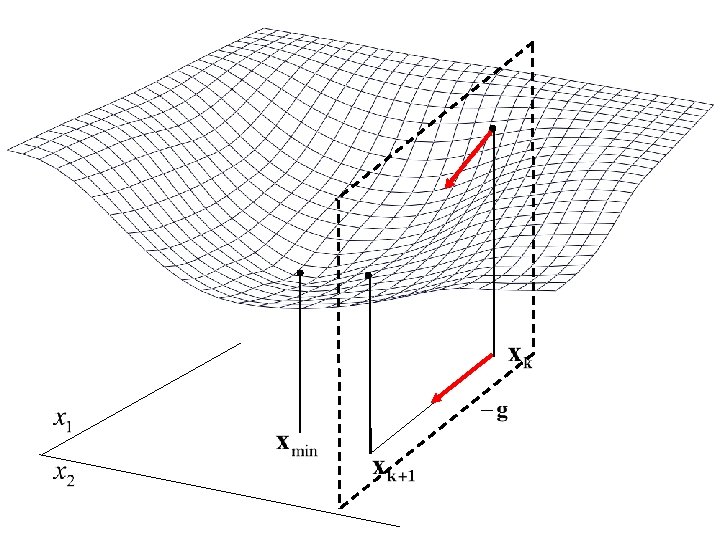
Pinhole camera model (X, Y, Z) P origin p (x, y) principal point (optical center)
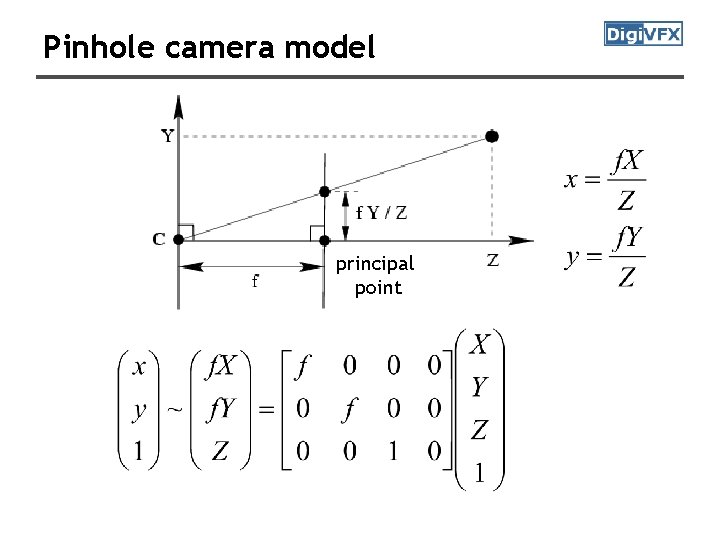
Pinhole camera model principal point
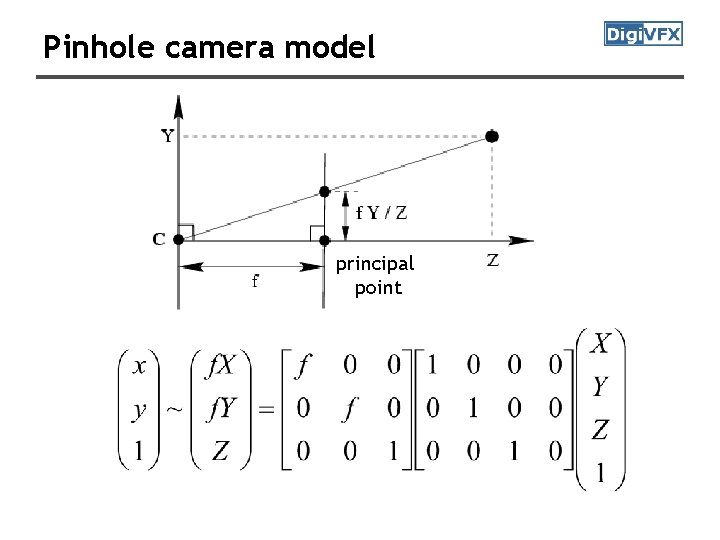
Pinhole camera model principal point
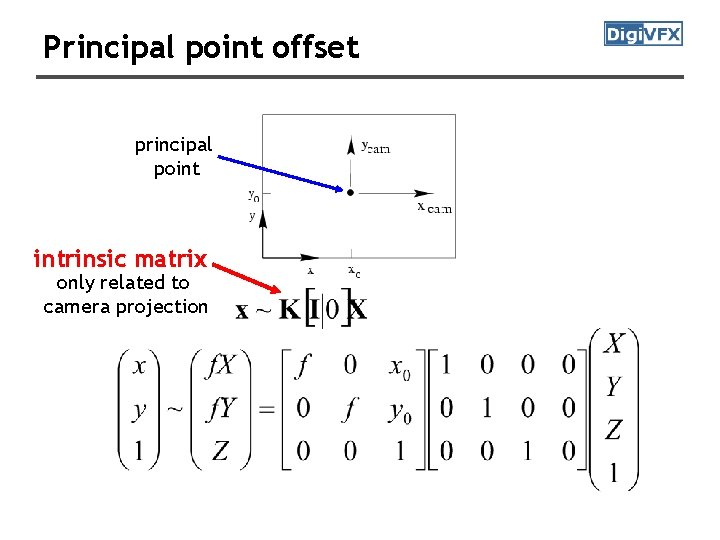
Principal point offset principal point intrinsic matrix only related to camera projection

Intrinsic matrix Is this form of K good enough? • non-square pixels (digital video) • skew • radial distortion

Distortion No distortion Pin cushion Barrel • Radial distortion of the image – Caused by imperfect lenses – Deviations are most noticeable for rays that pass through the edge of the lens
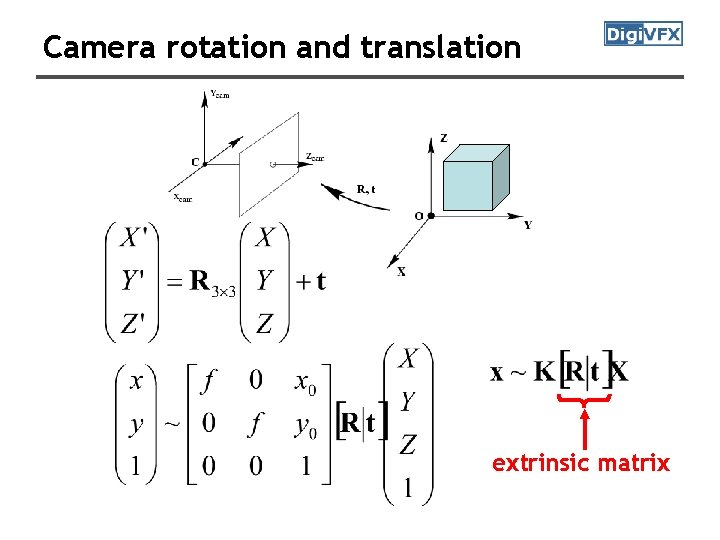
Camera rotation and translation extrinsic matrix

Two kinds of parameters • internal or intrinsic parameters such as focal length, optical center, aspect ratio: what kind of camera? • external or extrinsic (pose) parameters including rotation and translation: where is the camera?
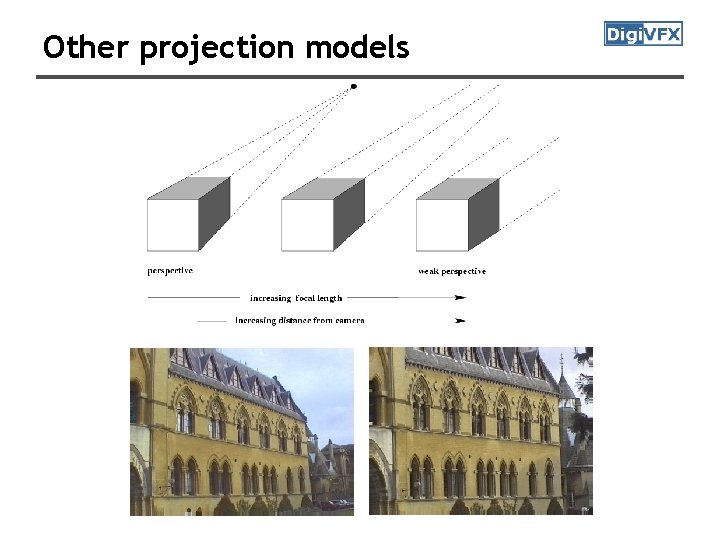
Other projection models
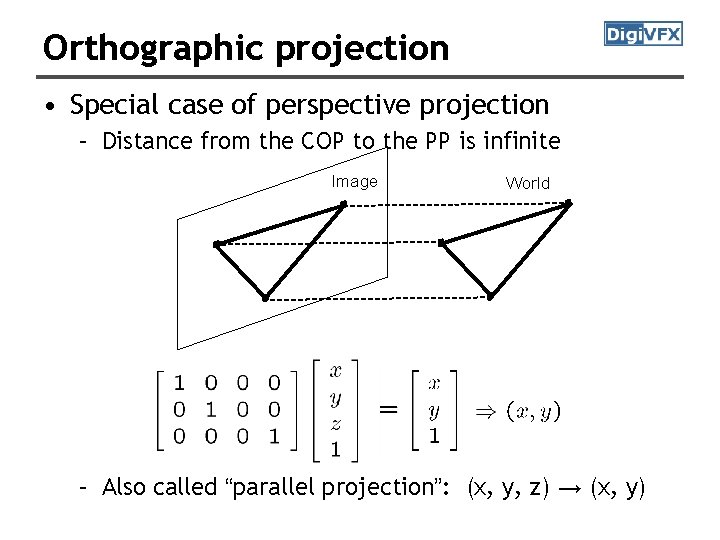
Orthographic projection • Special case of perspective projection – Distance from the COP to the PP is infinite Image World – Also called “parallel projection”: (x, y, z) → (x, y)
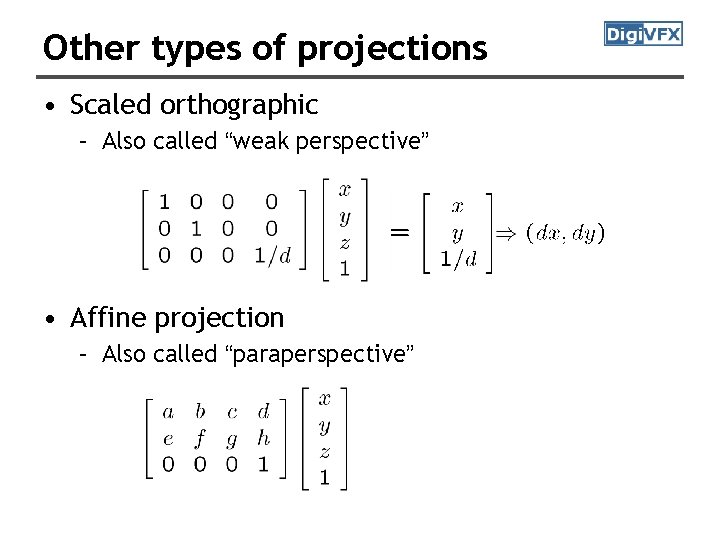
Other types of projections • Scaled orthographic – Also called “weak perspective” • Affine projection – Also called “paraperspective”
Illusion
Illusion
Fun with perspective
Perspective cues
Perspective cues
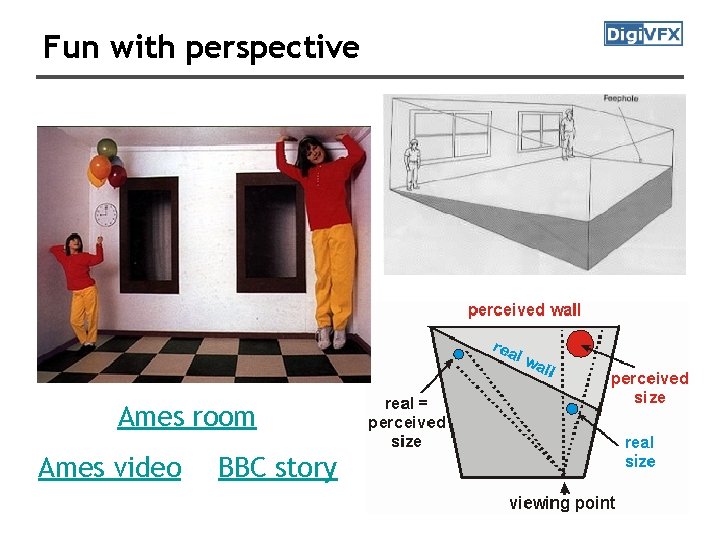
Fun with perspective Ames room Ames video BBC story

Forced perspective in LOTR

Camera calibration

Camera calibration • Estimate both intrinsic and extrinsic parameters. Two main categories: 1. Photometric calibration: uses reference objects with known geometry 2. Self calibration: only assumes static scene, e. g. structure from motion
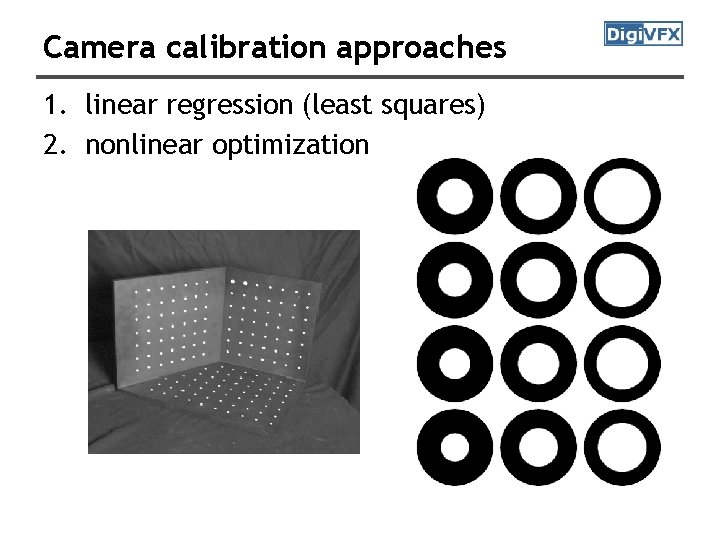
Camera calibration approaches 1. linear regression (least squares) 2. nonlinear optimization

Chromaglyphs (HP research)

Camera calibration
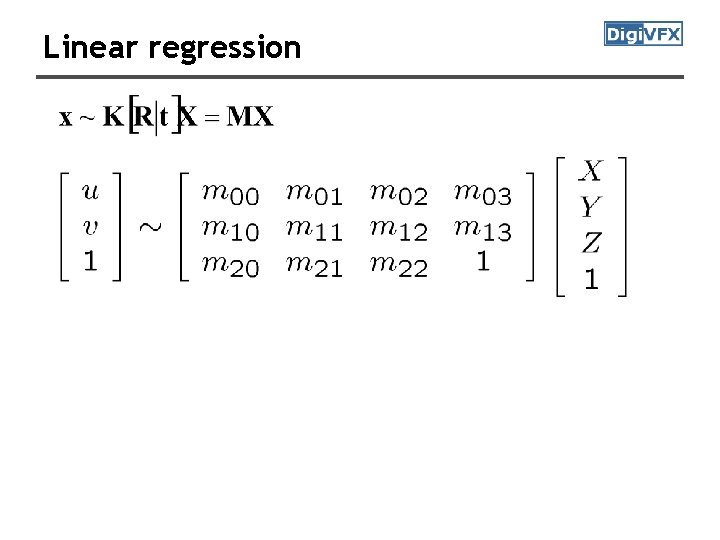
Linear regression

Linear regression • Directly estimate 11 unknowns in the M matrix using known 3 D points (Xi, Yi, Zi) and measured feature positions (ui, vi)

Linear regression

Linear regression

Linear regression Solve for Projection Matrix M using least-square techniques

Normal equation Given an overdetermined system the normal equation is that which minimizes the sum of the square differences between left and right sides

Linear regression • Advantages: – All specifics of the camera summarized in one matrix – Can predict where any world point will map to in the image • Disadvantages: – Doesn’t tell us about particular parameters – Mixes up internal and external parameters • pose specific: move the camera and everything breaks – More unknowns than true degrees of freedom

Nonlinear optimization • A probabilistic view of least square • Feature measurement equations • Probability of M given {(ui, vi)} P

Optimal estimation • Likelihood of M given {(ui, vi)} L P • It is a least square problem (but not necessarily linear least square) • How do we minimize L?

Optimal estimation • Non-linear regression (least squares), because the relations between ûi and ui are non-linear functions of M unknown parameters We could have terms like in this known constant • We can use Levenberg-Marquardt method to minimize it

Nonlinear least square methods

Least square fitting number of data points number of parameters
Linear least square fitting y t
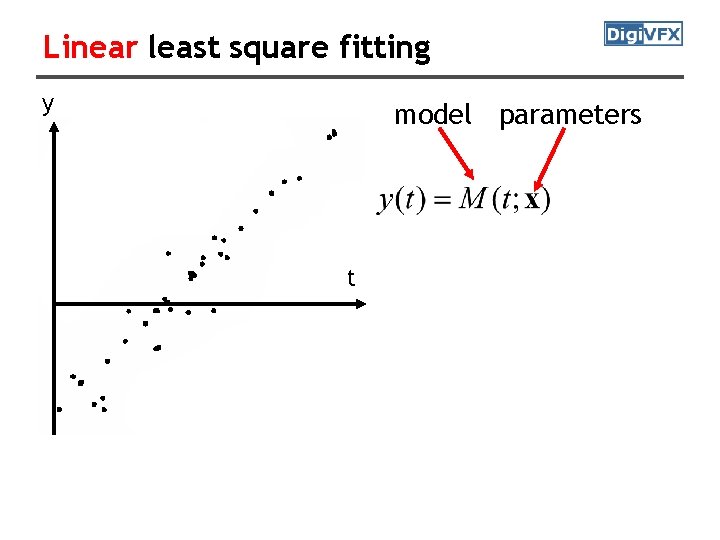
Linear least square fitting y model parameters t
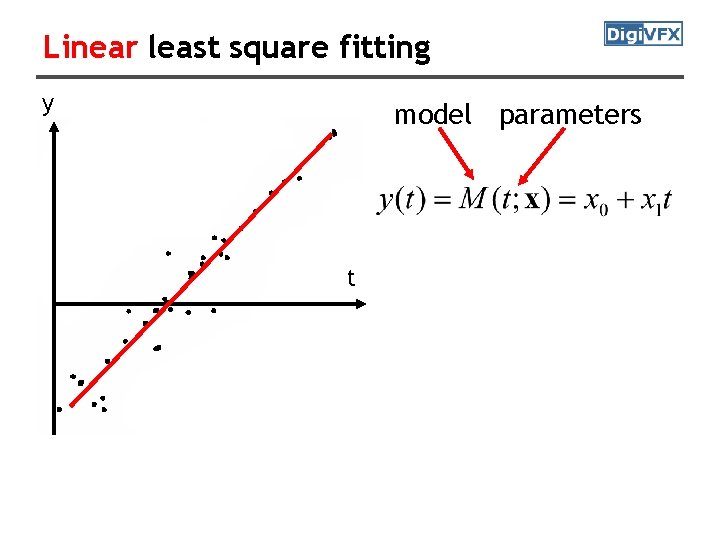
Linear least square fitting y model parameters t
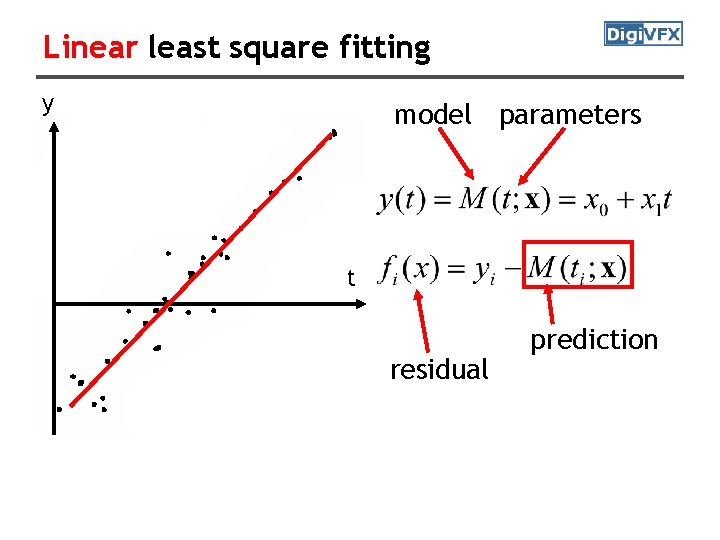
Linear least square fitting y model parameters t residual prediction
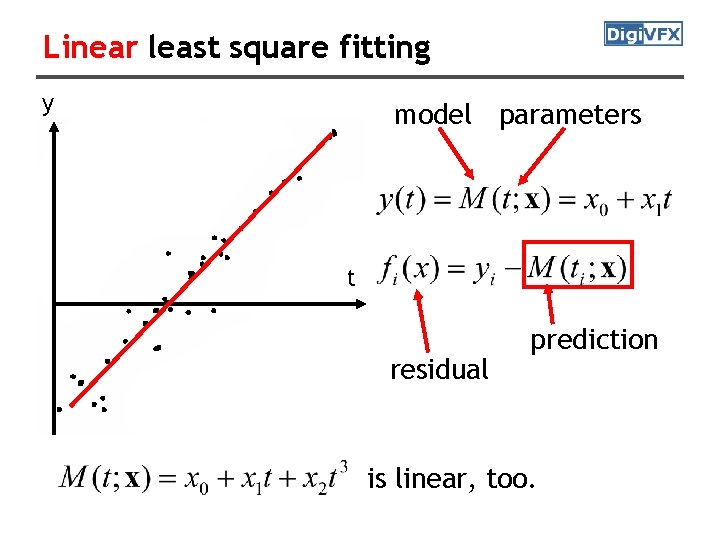
Linear least square fitting y model parameters t residual prediction is linear, too.

Nonlinear least square fitting model parameters residuals

Function minimization Least square is related to function minimization. It is very hard to solve in general. Here, we only consider a simpler problem of finding local minimum.

Function minimization
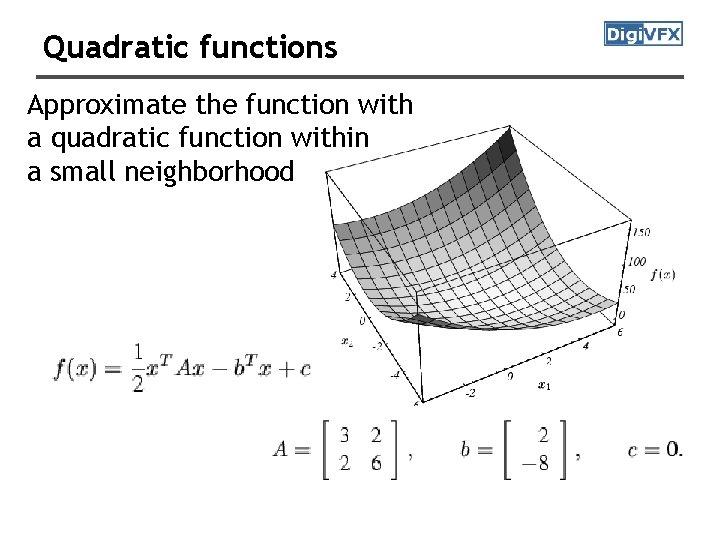
Quadratic functions Approximate the function with a quadratic function within a small neighborhood

Quadratic functions A is positive definite. All eigenvalues are positive. For all x, x. TAx>0. A is singular negative definite A is indefinite

Function minimization Why? By definition, if is small enough is a local minimizer,

Function minimization

Function minimization

Descent methods

Descent direction

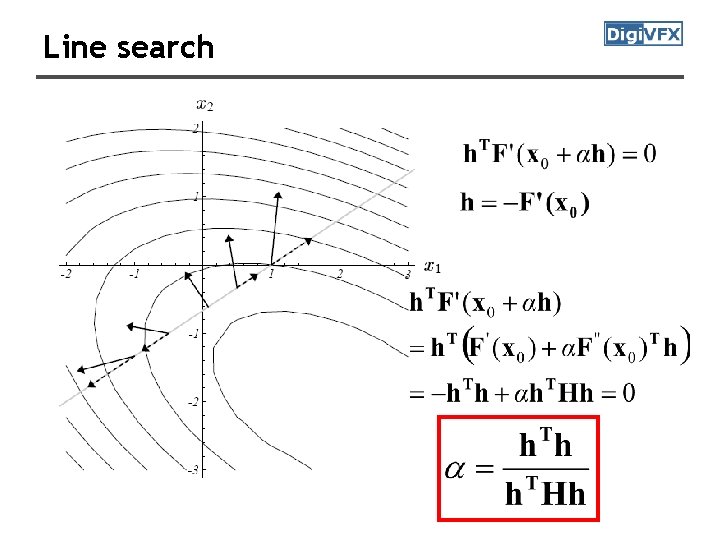
Steepest descent method the decrease of F(x) per unit along h direction → hsd is a descent direction because h. Tsd F’(x) = -F’(x)2 <0

Line search
Line search
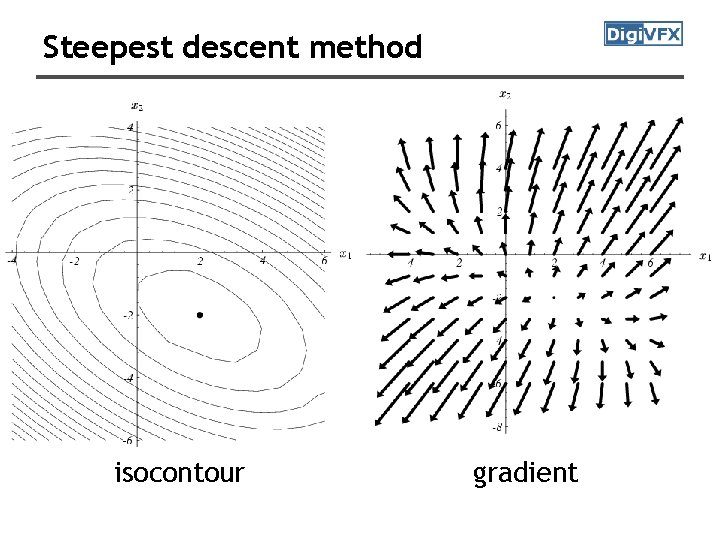
Steepest descent method isocontour gradient
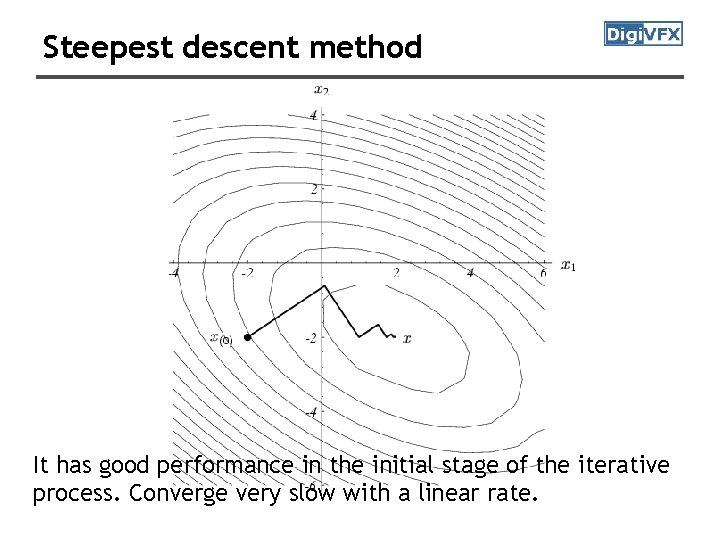
Steepest descent method It has good performance in the initial stage of the iterative process. Converge very slow with a linear rate.

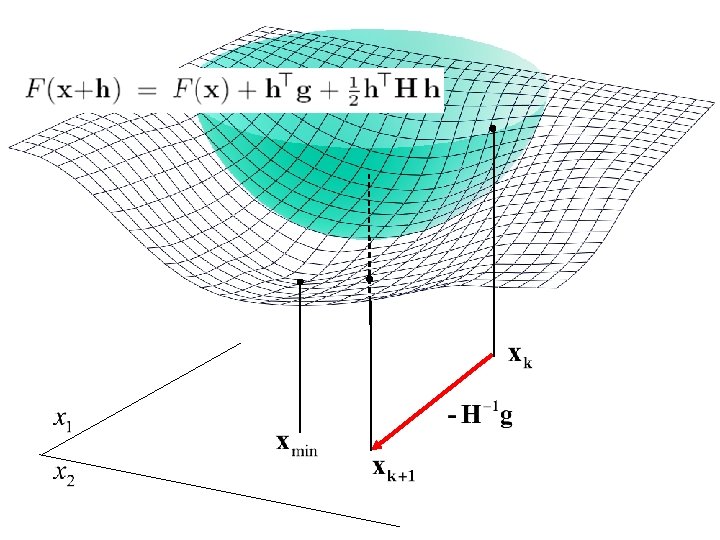
Newton’s method → →

Newton’s method • Another view • Minimizer satisfies

Newton’s method • It requires solving a linear system and H is not always positive definite. • It has good performance in the final stage of the iterative process, where x is close to x*.

Gauss-Newton method • Use the approximate Hessian • No need for second derivative • H is positive semi-definite

Hybrid method This needs to calculate second-order derivative which might not be available.

Levenberg-Marquardt method • LM can be thought of as a combination of steepest descent and the Newton method. When the current solution is far from the correct one, the algorithm behaves like a steepest descent method: slow, but guaranteed to converge. When the current solution is close to the correct solution, it becomes a Newton’s method.

Nonlinear least square

Levenberg-Marquardt method

Levenberg-Marquardt method • μ=0 → Newton’s method • μ→∞ → steepest descent method • Strategy for choosing μ – Start with some small μ – If F is not reduced, keep trying larger μ until it does – If F is reduced, accept it and reduce μ for the next iteration
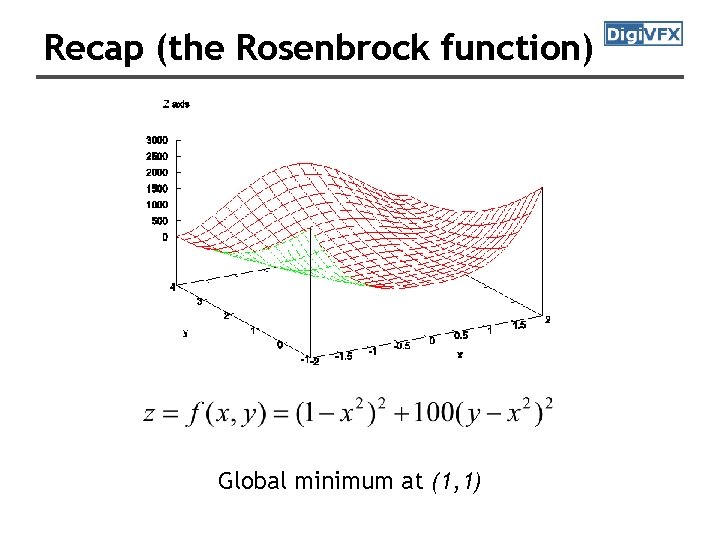
Recap (the Rosenbrock function) Global minimum at (1, 1)
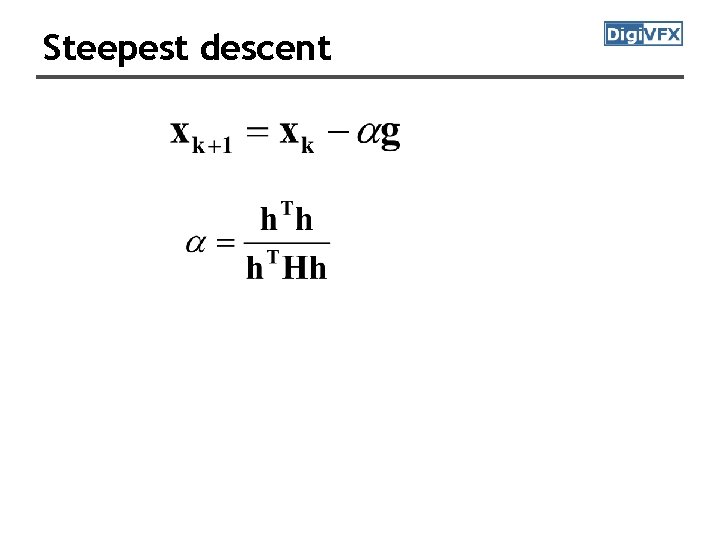
Steepest descent
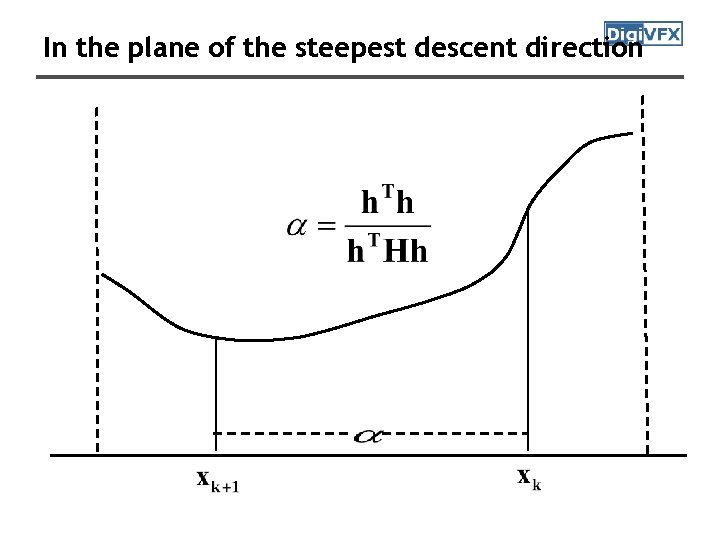
In the plane of the steepest descent direction
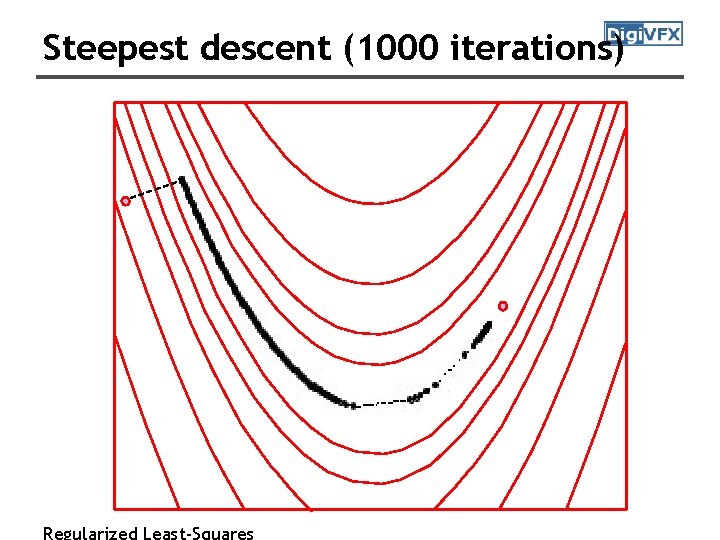
Steepest descent (1000 iterations) Regularized Least-Squares

Gauss-Newton method • With the approximate Hessian • No need for second derivative • H is positive semi-definite
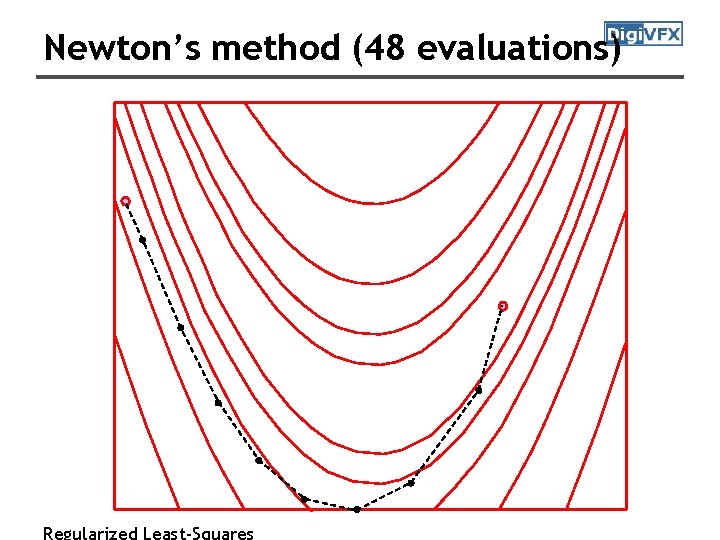
Newton’s method (48 evaluations) Regularized Least-Squares

Levenberg-Marquardt • Blends steepest descent and Gauss-Newton • At each step, solve for the descent direction h • If μ large, • If μ small, , steepest descent , Gauss-Newton
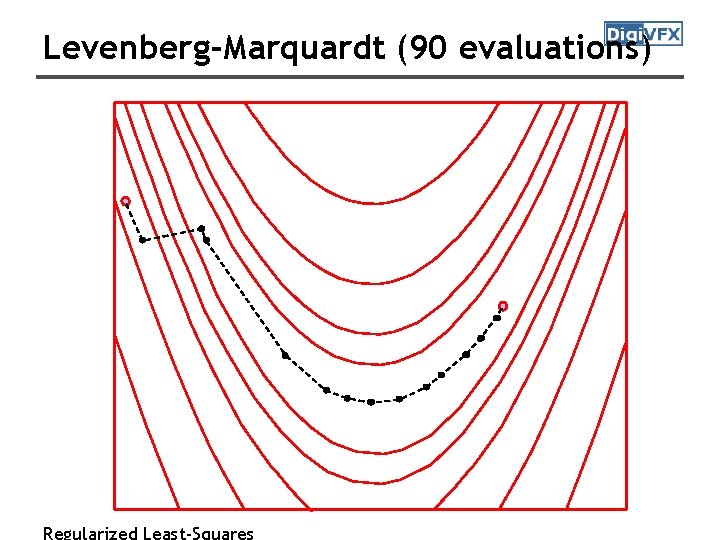
Levenberg-Marquardt (90 evaluations) Regularized Least-Squares

A popular calibration tool

Multi-plane calibration Advantage Images courtesy Jean-Yves Bouguet, Intel Corp. • Only requires a plane • Don’t have to know positions/orientations • Good code available online! – Intel’s Open. CV library: http: //www. intel. com/research/mrl/research/opencv/ – Matlab version by Jean-Yves Bouget: http: //www. vision. caltech. edu/bouguetj/calib_doc/index. html – Zhengyou Zhang’s web site: http: //research. microsoft. com/~zhang/Calib/

Step 1: data acquisition

Step 2: specify corner order

Step 3: corner extraction

Step 3: corner extraction
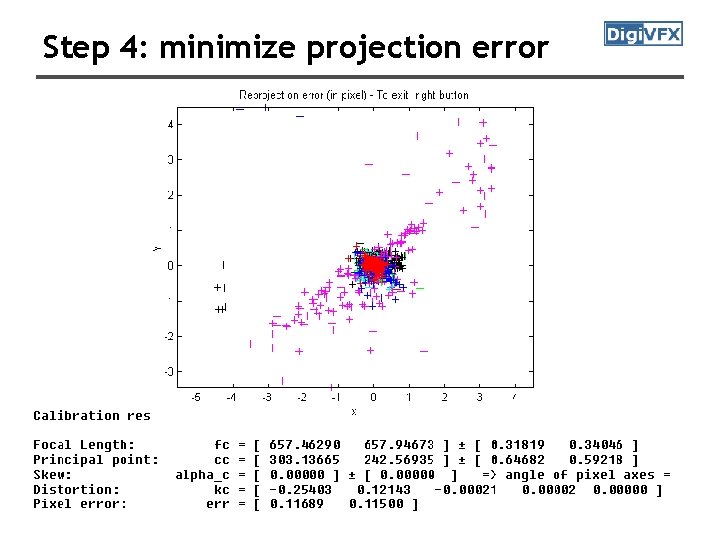
Step 4: minimize projection error
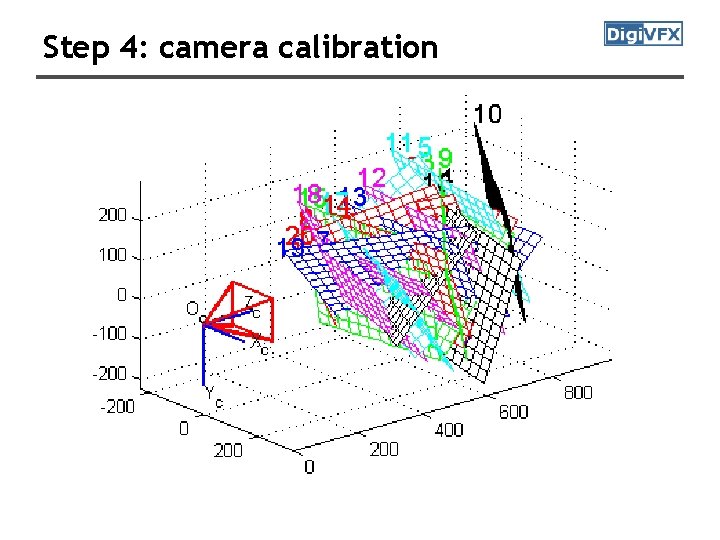
Step 4: camera calibration
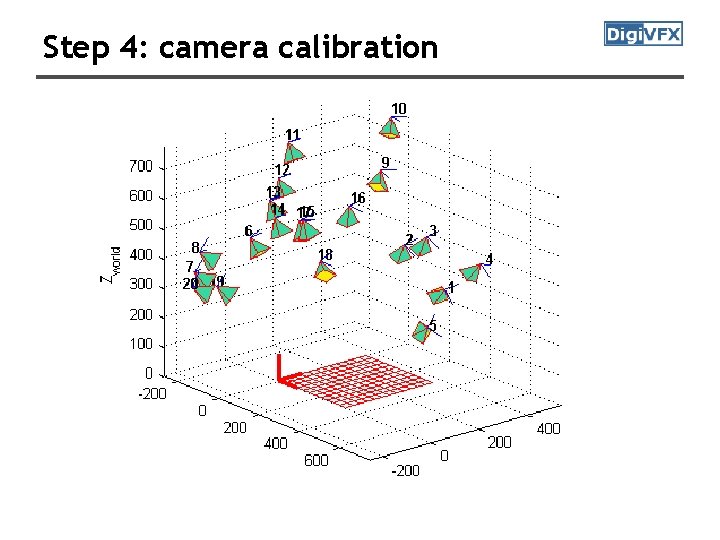
Step 4: camera calibration
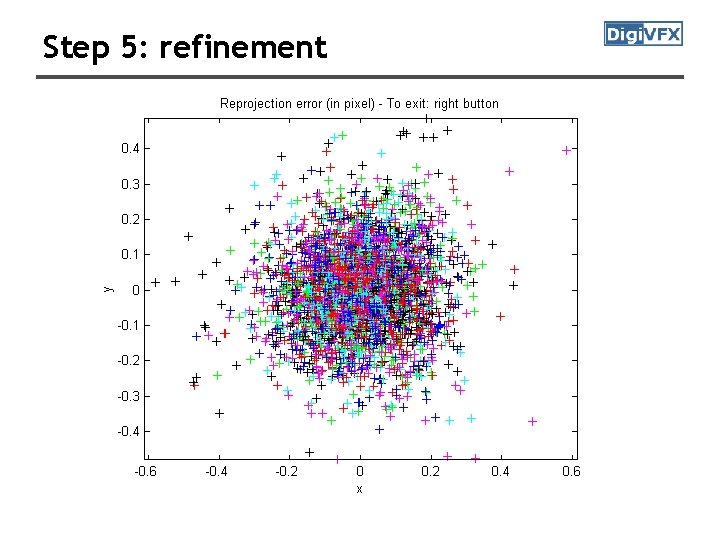
Step 5: refinement

Optimized parameters

Applications

How is calibration used? • Good for recovering intrinsic parameters; It is thus useful for many vision applications • Since it requires a calibration pattern, it is often necessary to remove or replace the pattern from the footage or utilize it in some ways…

Example of calibration

Example of calibration

Example of calibration • • • Videos from Ga. Tech Das. Tatoo, Make. Of P!NG, Make. Of Work, Make. Of Life. In. Paints, Make. Of

Photo. Book Make. Of
- Slides: 96