California Standards 21 0 Students graph quadratic functions

California Standards 21. 0 Students graph quadratic functions and know that their roots are the xintercepts. Also covered: 17. 0

Objective • Students Graph Quadratic functions and determine whether they have a minimum or a maximum

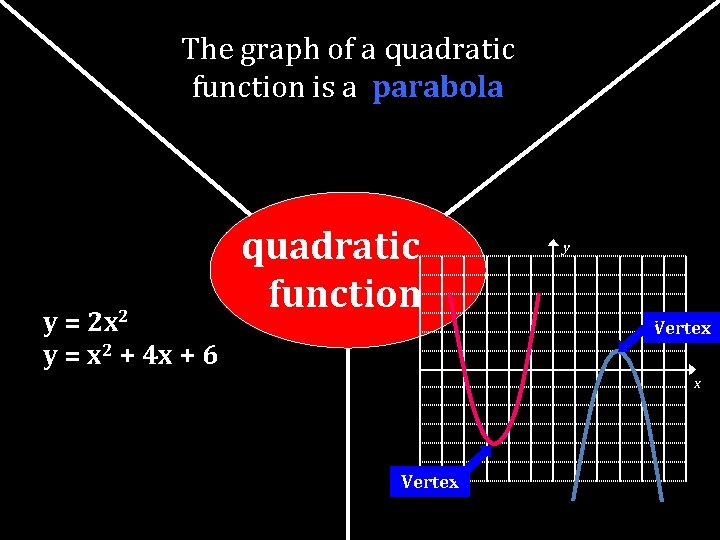
The graph of a quadratic function is a parabola y = 2 x 2 y = x 2 + 4 x + 6 quadratic function y Vertex x Vertex

Quadratic Equations and Their Graphs For any quadratic equation in two variables • all points on its graph are solutions to the equation. • all solutions to the equation appear on its graph.

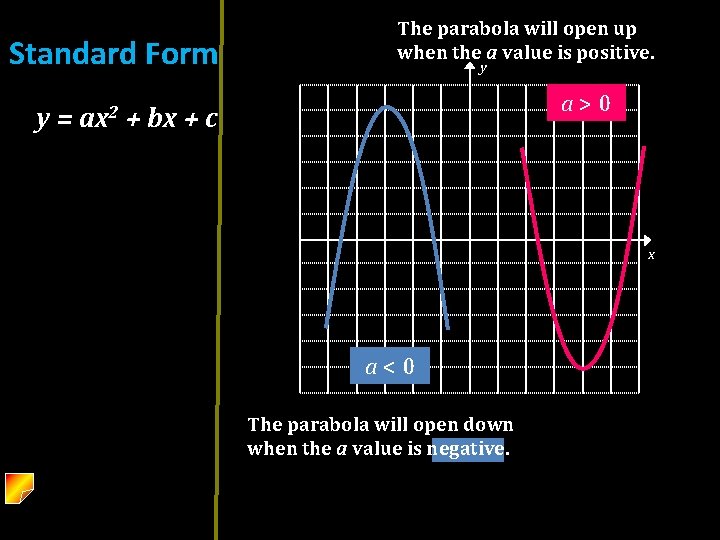
Standard Form y= ax 2 The parabola will open up when the a value is positive. y a>0 + bx + c x a<0 The parabola will open down when the a value is negative.

Without graphing, tell whether each Substitute (4, 16) into point is on the graph of =? 16 = (4, 16) 8 +8 16 = 16 Since (4, 16) is a solution of (4, 16) is on the graph.

Without graphing, Substitute (– 2, 10) into tell whether the function is on the graph of =? (– 2, 10) 10= 2+ 8 10 = 10 Since (– 2, 10) is a solution of (– 2, 10) is on the graph.

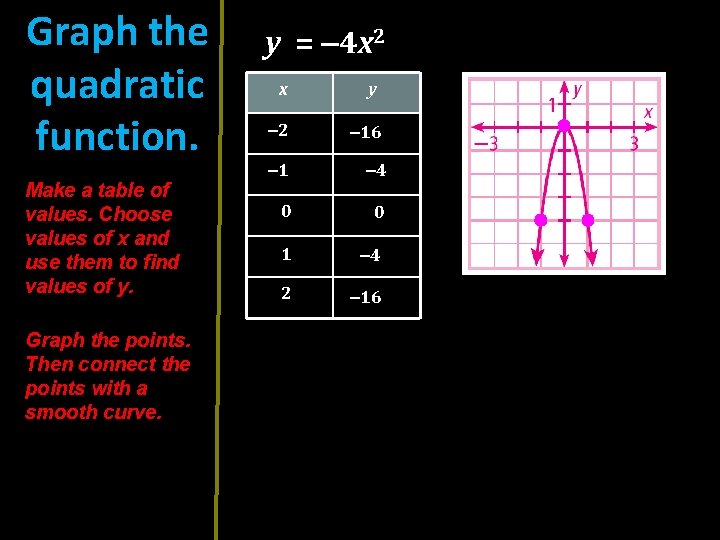
Graph the quadratic function. Make a table of values. Choose values of x and use them to find values of y. Graph the points. Then connect the points with a smooth curve. y = – 4 x 2 x y – 2 – 16 – 1 – 4 0 0 1 – 4 2 – 16

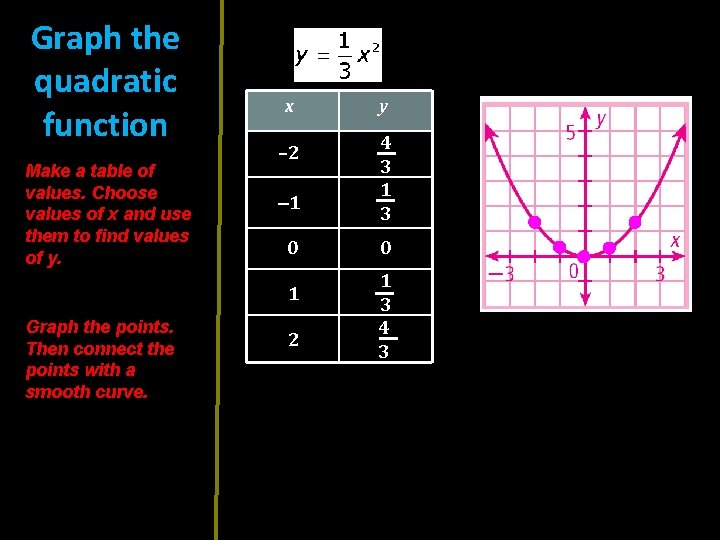
Summary: When choosing values of x, be sure to choose positive values, negative values, and 0.

Graph the quadratic function Make a table of values. Choose values of x and use them to find values of y. x – 2 – 1 0 1 Graph the points. Then connect the points with a smooth curve. 2 y 4 3 1 3 0 1 3 4 3

Tell whether the graph of the quadratic function opens upward or downward. Explain. Write the function in the form y = ax 2 + bx + c. Identify the value of a. y = 5 x – 3 x 2 y = – 3 x 2 + 5 x a = – 3 Since a < 0, the parabola opens downward.

Tell whether the graph of each quadratic function opens upward or downward. Explain. Identify the value of a. f(x) = – 4 x 2 – x + 1 a = – 4 Since a < 0 the parabola opens downward.

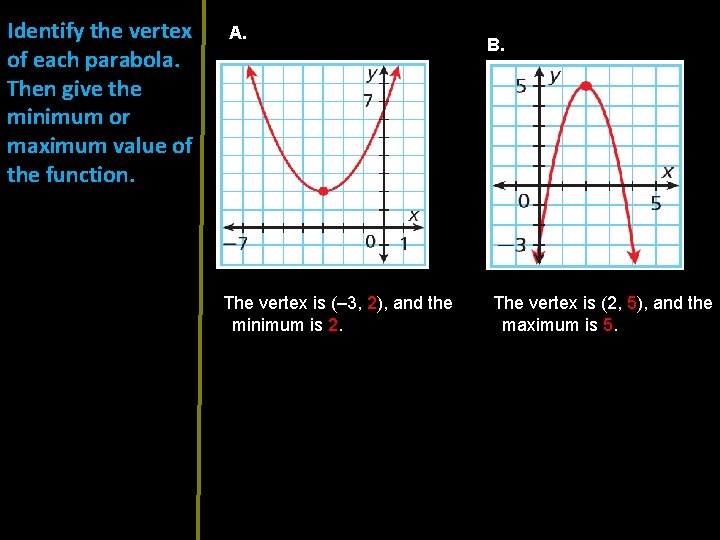
Identify the vertex of each parabola. Then give the minimum or maximum value of the function. A. The vertex is (– 3, 2), and the minimum is 2. B. The vertex is (2, 5), and the maximum is 5.

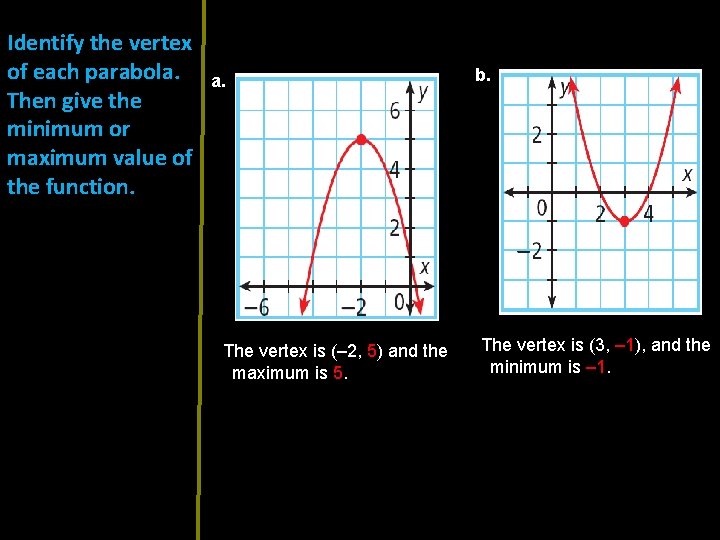
Identify the vertex of each parabola. Then give the minimum or maximum value of the function. a. The vertex is (– 2, 5) and the maximum is 5. b. The vertex is (3, – 1), and the minimum is – 1.

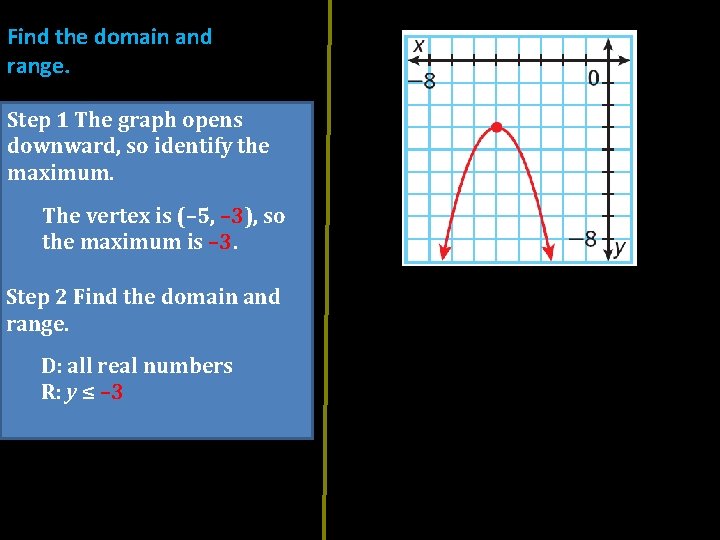
Find the domain and range. Step 1 The graph opens downward, so identify the maximum. The vertex is (– 5, – 3), so the maximum is – 3. Step 2 Find the domain and range. D: all real numbers R: y ≤ – 3

Find the domain and range. Step 1 The graph opens upward, so identify the minimum. The vertex is (– 2, – 4), so the minimum is – 4. Step 2 Find the domain and range. D: all real numbers R: y ≥ – 4

Summary: How do you know if the parabola open up are open downward?

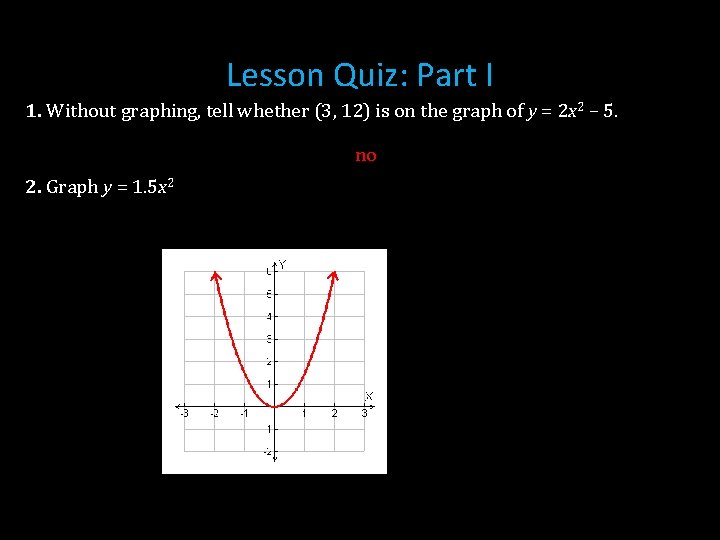
Lesson Quiz: Part I 1. Without graphing, tell whether (3, 12) is on the graph of y = 2 x 2 – 5. no 2. Graph y = 1. 5 x 2

Lesson Quiz: Part II Use the graph for Problems 3 -5. (5, – 4) 3. Identify the vertex. 4. Does the function have a minimum or maximum? What is it? maximum; – 4 5. Find the domain and range. D: all real numbers; R: y ≤ – 4