Calibration Guidelines Model development 1 Start simple add

Calibration Guidelines Model development 1. Start simple, add complexity carefully 2. Use a broad range of information 3. Be well-posed & be comprehensive 4. Include diverse observation data for ‘best fit’ 5. Use prior information carefully 6. Assign weights that reflect ‘observation’ error 7. Encourage convergence by making the model more accurate 8. Consider alternative models Model testing 9. Evaluate model fit 10. Evaluate optimal parameter values Potential new data 11. Identify new data to improve parameter estimates 12. Identify new data to improve predictions Prediction uncertainty 13. Use deterministic methods 14. Use statistical methods

Guideline 11: Identify New Data to Improve Model Parameter Estimates and Evaluate Potential for Additional Estimated Parameters Here we consider measurements related to observations because the connection between hydrologic and hydrogeologic data is direct and needs no special statistics. Hydrologic and hydrogeologic data Relate to model inputs Ground-Water Model -Parameters Dependent variable Observations Relate to model outputs Prediction uncertainty Societal decisions

Potential new observations to improve parameter estimates • Goal: evaluate worth of the type and location of potential observations. No observed value yet, so need statistics that don’t depend on this value. Use fit-independent statistics • In the context of reducing parameter uncertainty and increasing uniqueness, use the statistics: A. Dimensionless scaled sensitivities. B. One-percent scaled sensitivities. Often plotted in map form. C. Parameter correlation coefficients D. Leverage statistics E. Influence statistics (not discussed here) A. Dimensionless scaled sensitivities (dss): • • • Can be calculated for any potential observation type or location Account for the expected accuracy of the measurements because dss include the observation weight. Larger values identify observations that are likely to reduce parameter uncertainty.

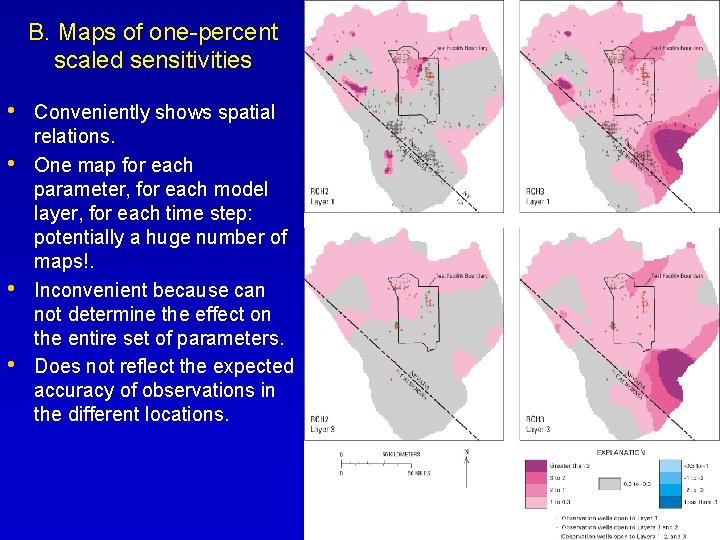
B. Maps of one-percent scaled sensitivities • • Conveniently shows spatial relations. One map for each parameter, for each model layer, for each time step: potentially a huge number of maps!. Inconvenient because can not determine the effect on the entire set of parameters. Does not reflect the expected accuracy of observations in the different locations.

C. Parameter correlation coefficients Calculate without and with the potential new data. If correlations with absolute values close to 1. 00 become smaller, the new data will help attain unique parameter estimates. Example from Cape Cod (Anderman and others 1996; Anderman and Hill 2001) • Clearly illustrates that collecting flow and advective transport data can radically reduce the extreme parameter correlations that occur when only head are used.

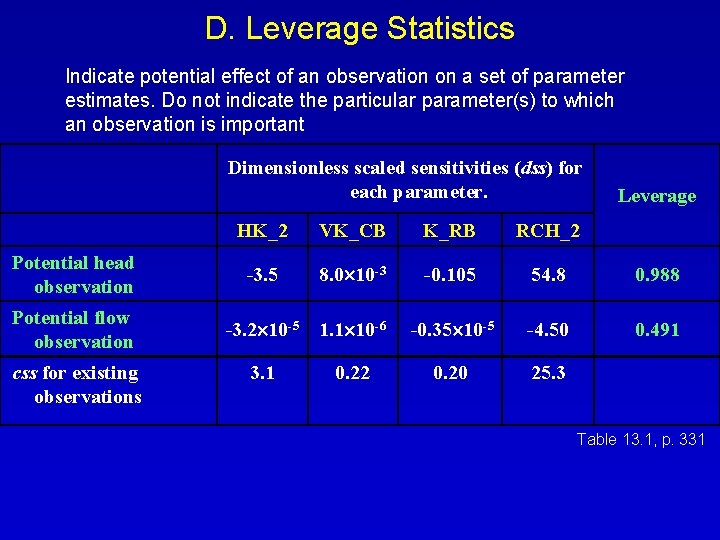
D. Leverage Statistics Indicate potential effect of an observation on a set of parameter estimates. Do not indicate the particular parameter(s) to which an observation is important Dimensionless scaled sensitivities (dss) for each parameter. Leverage HK_2 VK_CB K_RB RCH_2 Potential head observation -3. 5 8. 0 10 -3 -0. 105 54. 8 0. 988 Potential flow observation -3. 2 10 -5 1. 1 10 -6 -0. 35 10 -5 -4. 50 0. 491 3. 1 0. 22 0. 20 25. 3 css for existing observations Table 13. 1, p. 331

Evaluation of possible additional estimated parameters What parameters could be supported in more detail, given the information in the observations? Use css

Calibration Guidelines Model development 1. Start simple, add complexity carefully 2. Use a broad range of information 3. Be well-posed & be comprehensive 4. Include diverse observation data for ‘best fit’ 5. Use prior information carefully 6. Assign weights that reflect ‘observation’ error 7. Encourage convergence by making the model more accurate 8. Consider alternative models Model testing 9. Evaluate model fit 10. Evaluate optimal parameter values Potential new data 11. Identify new data to improve parameter estimates 12. Identify new data to improve predictions Prediction uncertainty 13. Use deterministic methods 14. Use statistical methods

Guideline 12: Identify New Data to Improve Model Predictions Two categories of potential new data: Measurements related to observations and hydrology and hydrogeology Hydrologic and hydrogeologic data Relate to model inputs Ground-Water Model -Parameters Dependent variable Observations Relate to model outputs Prediction uncertainty Societal decisions

Potential new data to improve predictions – What existing or new observations are important to predictions? • Observation-Prediction Statistic (opr) – Which parameters are important to predictions? Infer important hydrologic and hydrogeologic data • Prediction scaled sensitivities (pss) with composite scaled sensitivies (css) and parameter correlation coefficients (pcc) • Parameter-Prediction Statistic (ppr)

Potential new observations to improve predictions Hydrologic and hydrogeologic data Relate to model inputs Ground-Water Model -Parameters Dependent variable Observations Relate to model outputs Prediction uncertainty Societal decisions Approach: OPR

Potential new observations to improve predictions Observation-Prediction (opr) Statistic • Which existing observations are important to predictions? – opr indicates the percent increase in prediction uncertainty caused by omitting an existing observation • What new observations would be most valuable to predictions? – opr indicates the percent decrease in prediction uncertainty caused by adding a new observation • Advantages: – Combines dss, dss css, and pss into one statistic that also accounts for parameter correlation – is independent of model fit – is computationally manageable

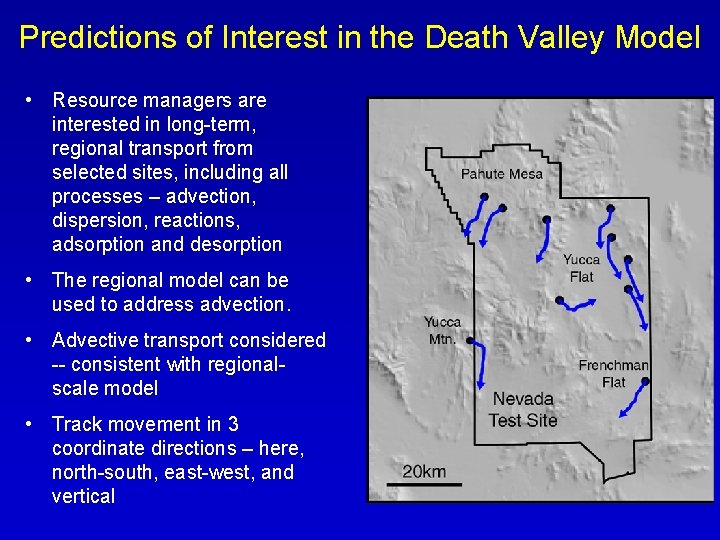
Predictions of Interest in the Death Valley Model • Resource managers are interested in long-term, regional transport from selected sites, including all processes – advection, dispersion, reactions, adsorption and desorption • The regional model can be used to address advection. • Advective transport considered -- consistent with regionalscale model • Track movement in 3 coordinate directions – here, north-south, east-west, and vertical

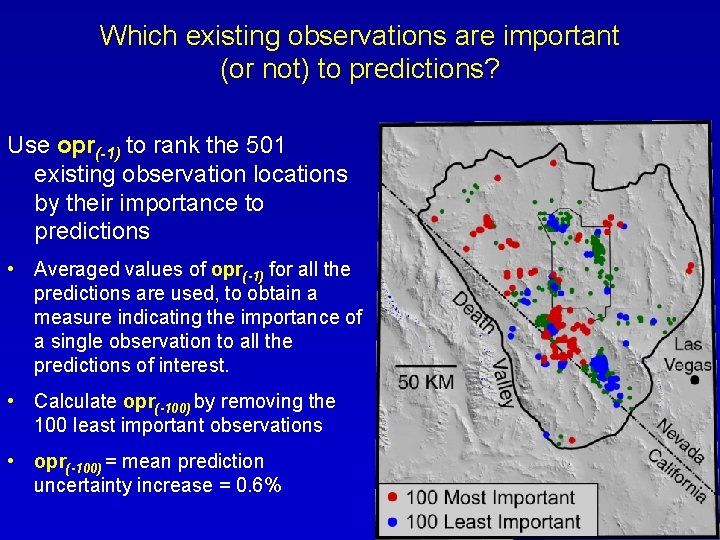
Which existing observations are important (or not) to predictions? Use opr(-1) to rank the 501 existing observation locations by their importance to predictions • Averaged values of opr(-1) for all the predictions are used, to obtain a measure indicating the importance of a single observation to all the predictions of interest. • Calculate opr(-100) by removing the 100 least important observations • opr(-100) = mean prediction uncertainty increase = 0. 6%

What new observations would be important (or not) to predictions? Consider potential new head observations in layer 1. Calculate opr(+1) for each cell in the layer.

Potential new data to improve predictions – What existing or new observations are important to predictions? • Observation-Prediction Statistic (opr) – Which parameters are important to predictions? Infer important hydrologic and hydrogeologic data • Prediction scaled sensitivities (pss) with composite scaled sensitivies (css) and parameter correlation coefficients (pcc) • Parameter-Prediction Statistic (ppr)

Potential new system property information to improve predictions Hydrologic and hydrogeologic data Relate to model inputs Ground-Water Model -Parameters Dependent variable Observations Relate to model outputs Prediction uncertainty Societal decisions Two approaches: A. Prediction scaled sensitivities (pss) together with composite scaled sensitivities (css) and parameter correlations (pcc) B. Parameter-prediction (ppr) statistic

A. Prediction Scaled Sensitivities (pss): What parameters are important to predictions? Here, pss are scaled to equal percent change in prediction caused by 1% change in parameter value pssdesired model complexity

css – supported model complexity pss – desired model complexity

B. Parameter-Prediction (ppr) Statistic • Which parameters are important to predictions? – ppr indicates percent decrease in prediction uncertainty caused by a decrease in parameter uncertainty. • The decrease in parameter uncertainty is implemented by increasing the weight on prior information for the parameter(s). • This increase in weight represents the increased certainty that would result from collection of additional field data about the parameter or associated system property.

Predictions of Interest in the Death Valley Model (simulations from the 3 -layer model of D’Agnese +, 1998) Apply ppr statistic to one prediction on Yucca Flat

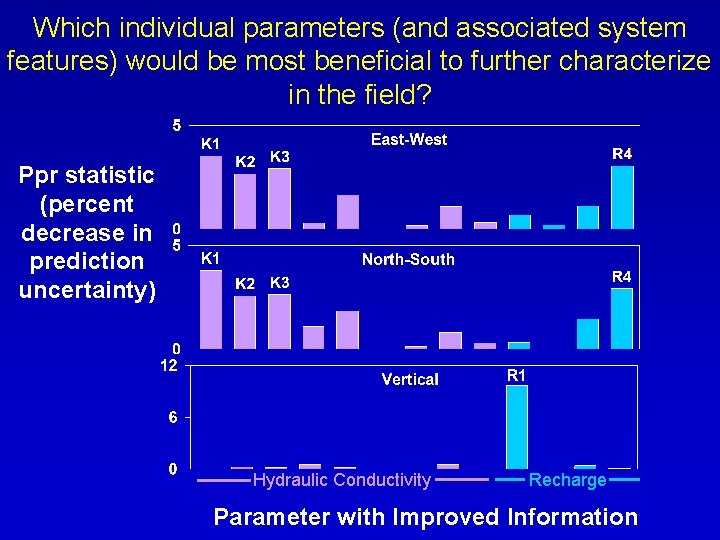
Which individual parameters (and associated system features) would be most beneficial to further characterize in the field? Ppr statistic (percent decrease in prediction uncertainty) Hydraulic Conductivity Recharge Parameter with Improved Information

Pros and cons of A (pss+) and B (ppr) A. Prediction scaled sensitivities (pss) together with composite scaled sensitivities (css) and parameter correlations (pcc) – – – B. PRO: pss, css, and pcc are each conceptually easy to understand convey to others PRO: independent of model fit and computationally manageable CON: Can be cumbersome to evaluate three measures to determine the value of new system property data Parameter-prediction (ppr) statistic – – – PRO: Combines css, css pss, and pcc into one statistic PRO: independent of model fit and computationally manageable CON: More conceptually difficult to understand explain to others. Best so far -- express in terms of percent changes in prediction uncertainty