Calculus Limits Continuity of Functions Differentiation Application of


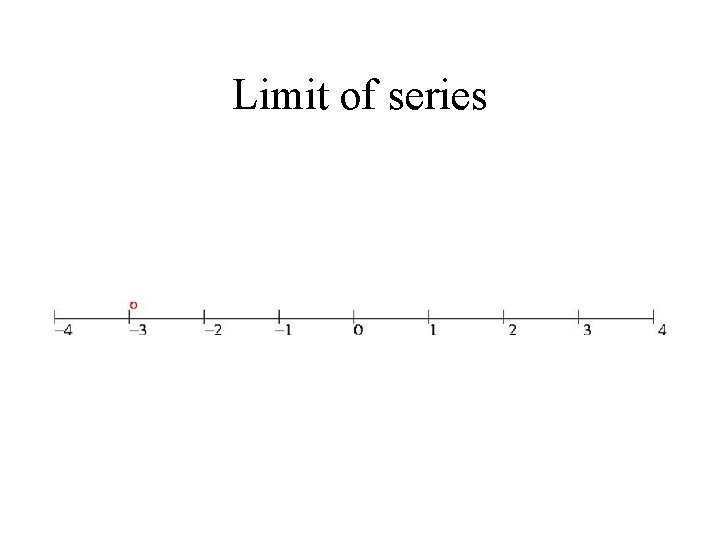
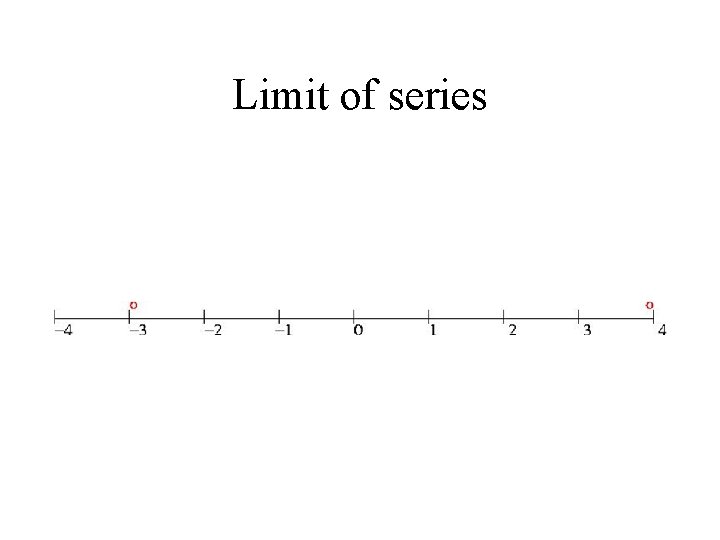
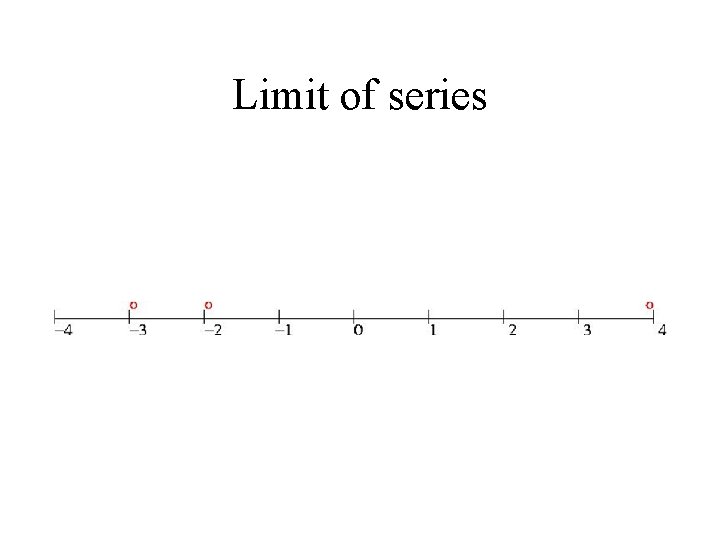
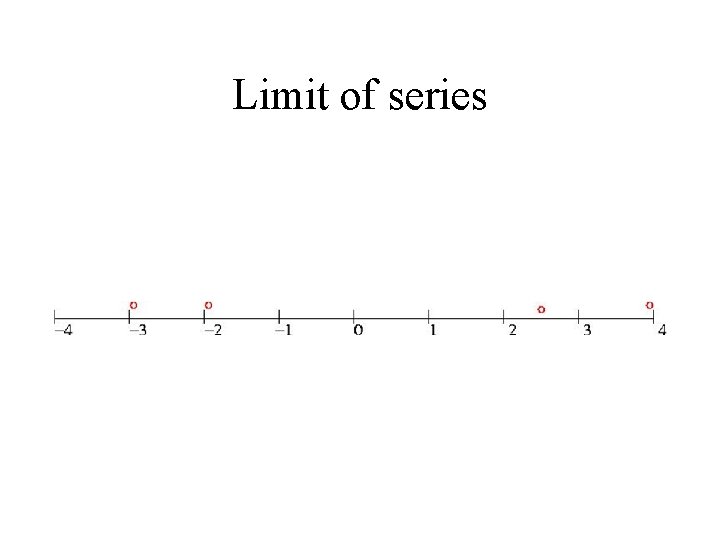
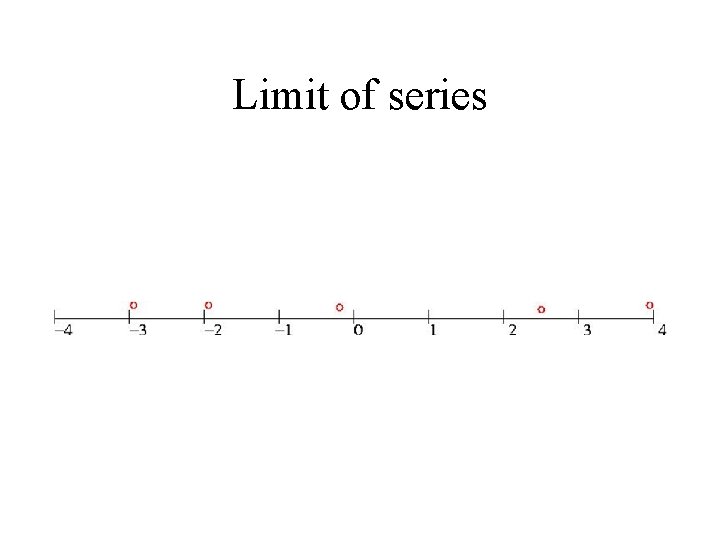
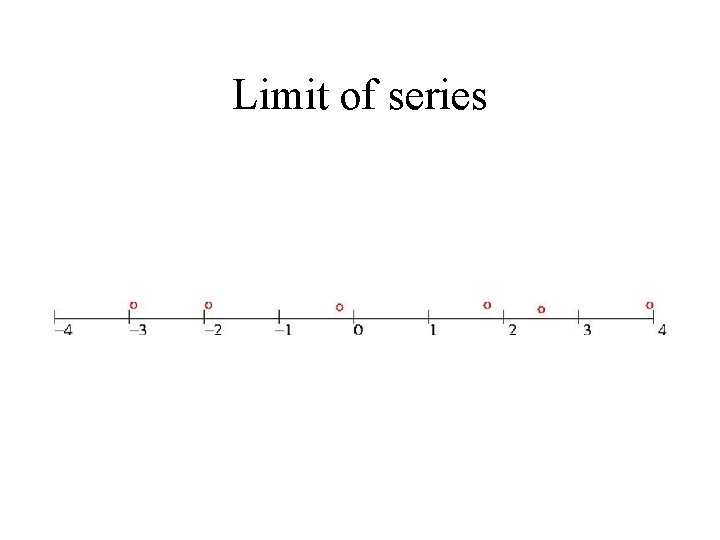
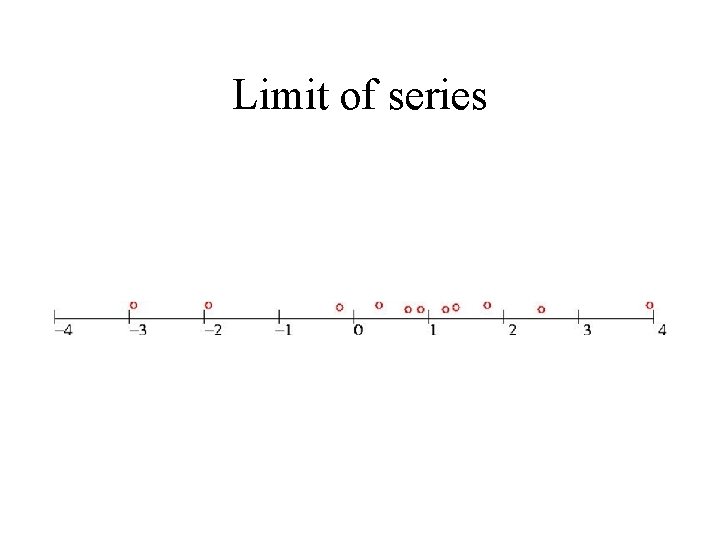



![A practical Example • Interest compounded continuously • S = P[(1 + r/k)^(kn)] where A practical Example • Interest compounded continuously • S = P[(1 + r/k)^(kn)] where](https://slidetodoc.com/presentation_image/55172902610d20bceb58f1460a057a1c/image-13.jpg)





































- Slides: 55

Calculus • • • Limits Continuity of Functions Differentiation Application of differentiation Integration

Limits • Example from tangent line • Example from Decimal expansion of 1/3=0. 33333…. • Definition of limits – get closer but do not touch • Few more examples of limits
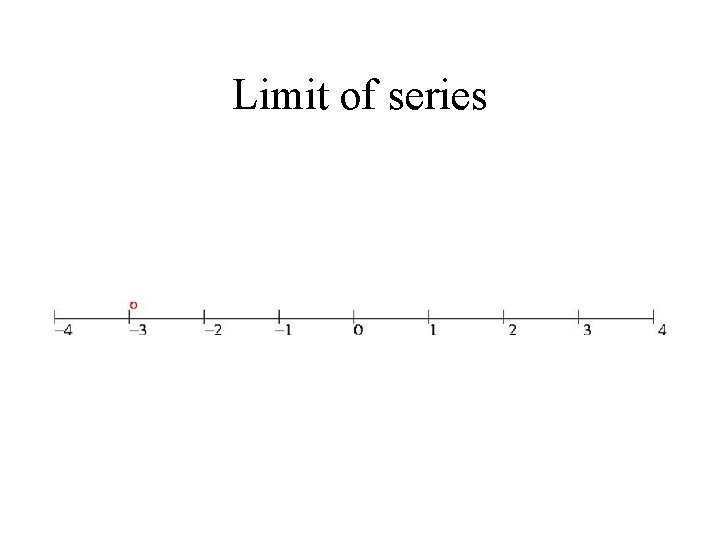
Limit of series
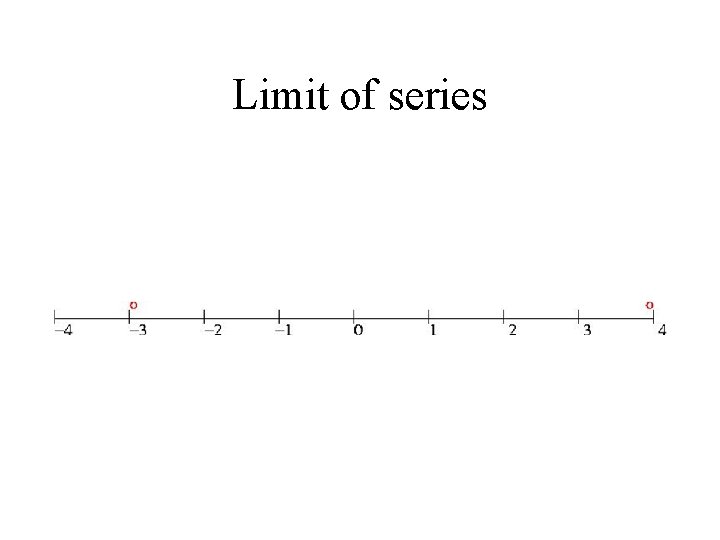
Limit of series
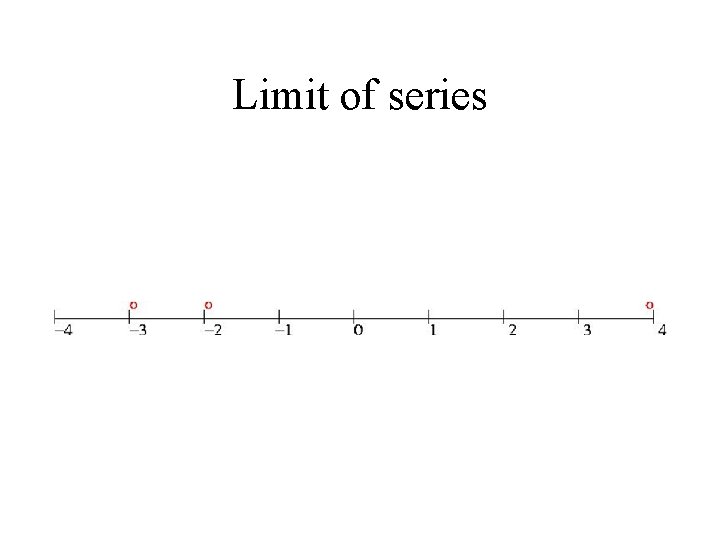
Limit of series
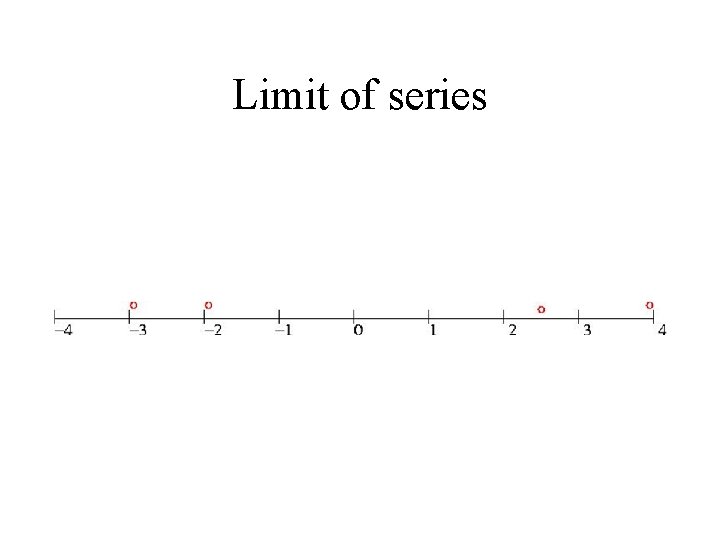
Limit of series
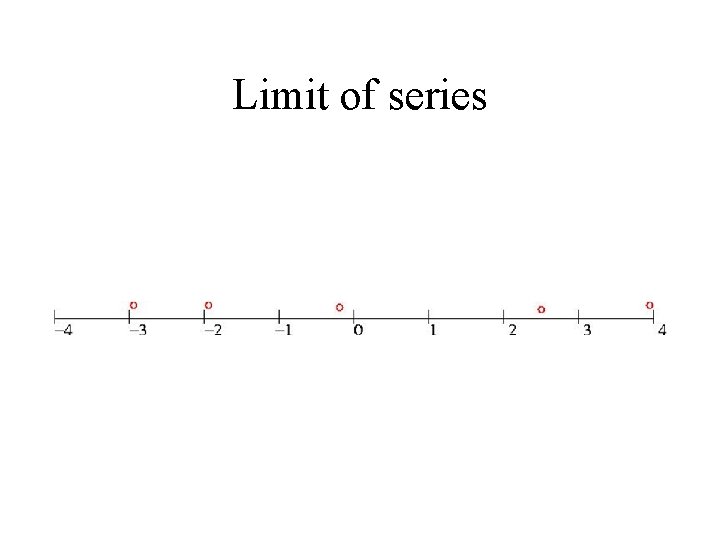
Limit of series
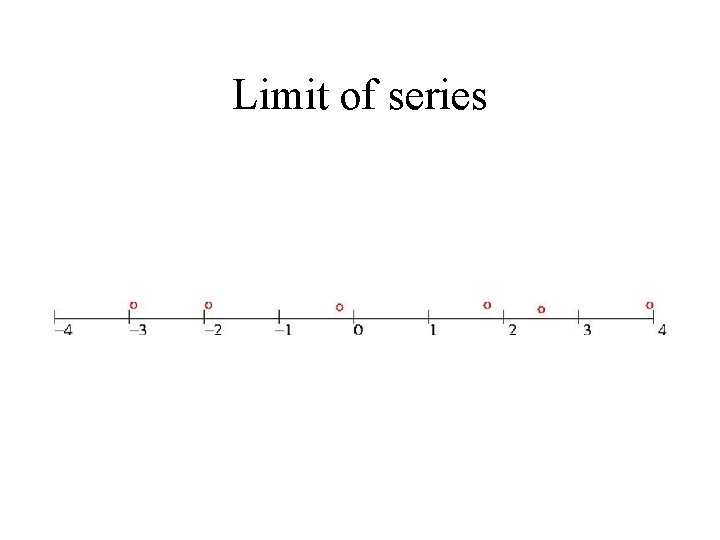
Limit of series
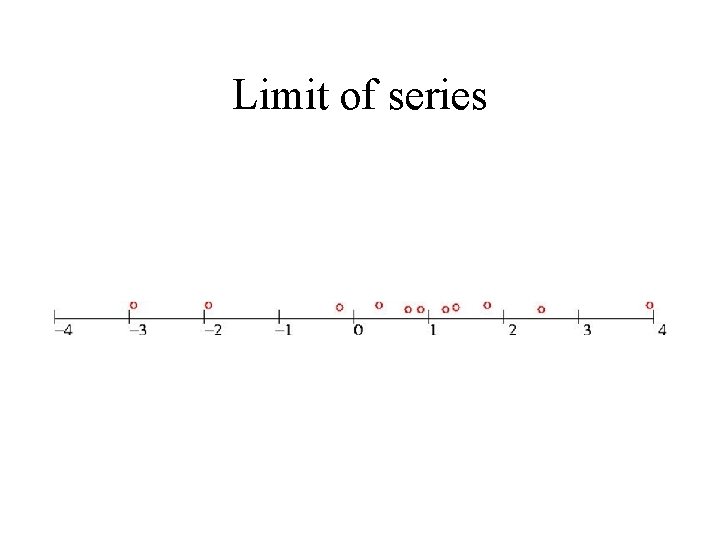
Limit of series

Limit of series

Limits • Example from geometric series • Limit of a series • Definition of limits – get closer but do not touch • Few more examples of limits

Some Important Limits • • • sin(x)/x at x=0 Definition of e Limit of 1/x at x=0 Limit of 1/(x*x) at x=0 more examples
![A practical Example Interest compounded continuously S P1 rkkn where A practical Example • Interest compounded continuously • S = P[(1 + r/k)^(kn)] where](https://slidetodoc.com/presentation_image/55172902610d20bceb58f1460a057a1c/image-13.jpg)
A practical Example • Interest compounded continuously • S = P[(1 + r/k)^(kn)] where n– no of years, k is no of times interest is compounded in a year, other variables have usual meaning. • Let k -> infinity. • S = P* e^(rn) • E. g. a trust fund is set by a single payment so that at the end of 20 years, there is $25000 in the fund. If the interest is calculated at a rate of 7% compounded continuously, find the amount of money to be invested.

Continuity • Definition • f(x)=1/x if x� ‚ 0; is f(x) continuous at x=0? • f(x)=1/x if x� ‚ 0 otherwise f(x)=0; is f continuous at x=0? • f(x)=x^2/x if x� ‚ 0 otherwise f(x)=1; is f continuous at x=0? • f(x)=x^2/x if x� ‚ 0 otherwise f(x)=0; is f continuous at x=0?

Feeling Continuity

Feeling Continuity

Feeling Continuity

Feeling Continuity

Feeling Continuity

Feeling Continuity

Feeling Continuity

Feeling Continuity

Feeling Continuity

Feeling Continuity

A discontinuous Function

A discontinuous Function

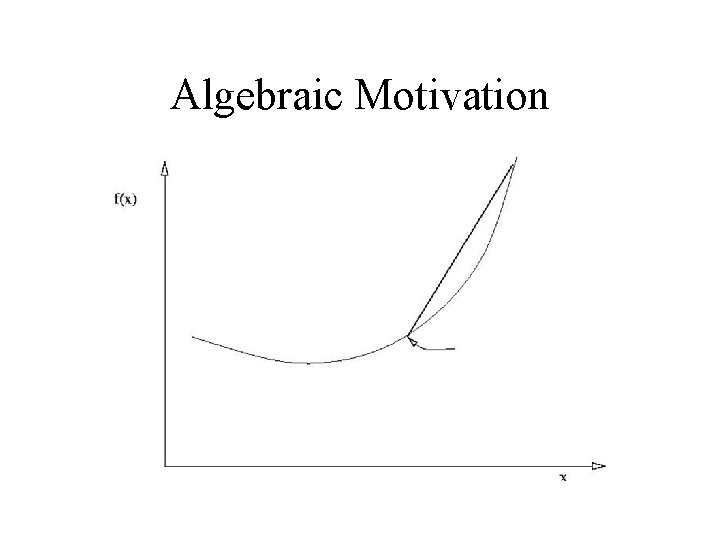
Differentiation • Algebraic motivation – rate of change

Algebraic Motivation

Algebraic Motivation

Algebraic Motivation

Algebraic Motivation

Algebraic Motivation

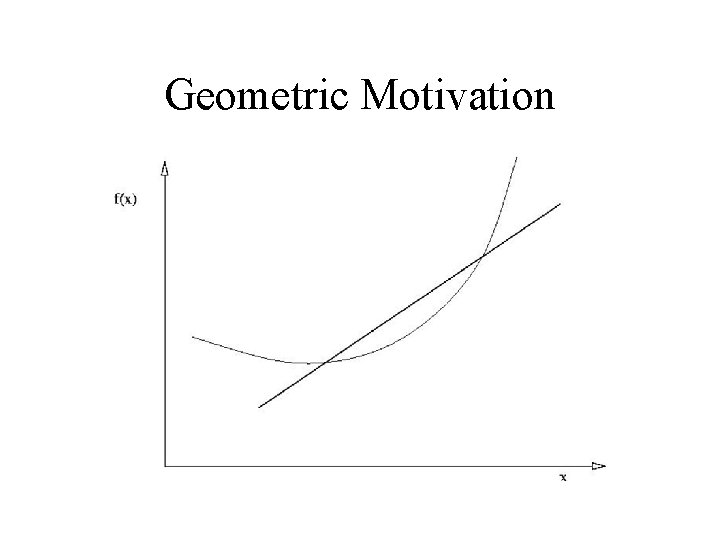
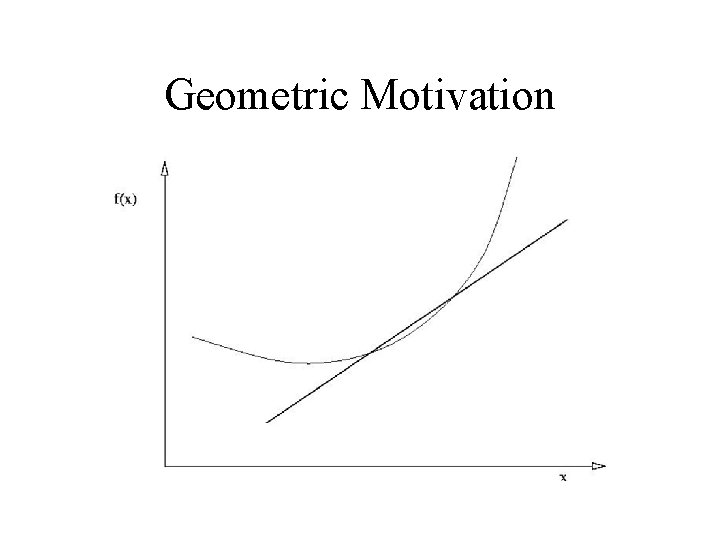
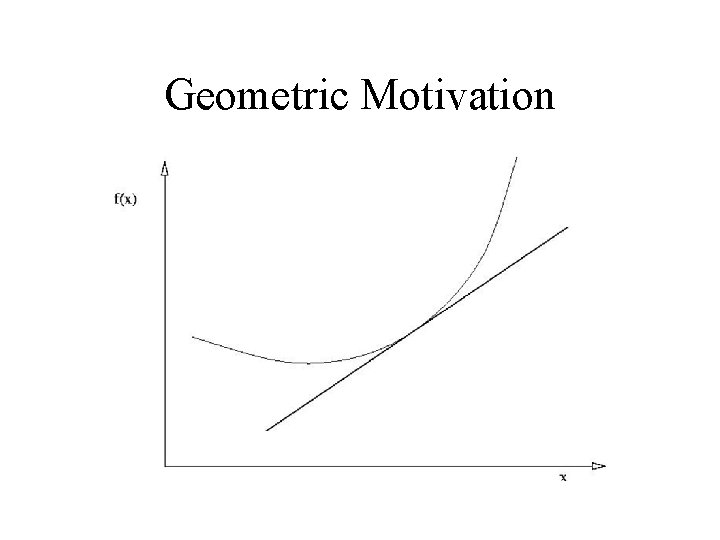
Differentiation • Algebraic motivation – rate of change • Geometric motivation – limiting position of secant

Geometric Motivation

Geometric Motivation

Geometric Motivation

Geometric Motivation

Geometric Motivation

Differentiation • • Definition Rules of Differentiation Examples Differentiable Functions

Feeling Differentiation

Feeling Differentiation

Feeling Differentiation

Some more Differentiation • • • Derivatives of Logarithmic functions Derivatives of Exponential functions Derivative of implicit functions examples Higher Order Derivatives

Multivariate Calculus • Functions of Several Variables – E. g. The marketing quantity may depend on the own price and price of competition. – Represented in a 3 -D plane rather than a line. – Important in complex dependency models

Partial Differentiation • Rate of change of function when one variable changes • example

Applications of Partial Derivatives • E. g. A company manufactures two types of products A and B. Suppose the joint cost function for producing x pairs of A and y pairs of B is • C = 0. 06 x*x + 65 x + 75 y + 1000 • Determine the marginal costs wrt x and y and evaluate these when x = 100 and y = 50. Interpret.

Applications of Partial Derivatives • E. g. MBA compensation : In a study of success among MBAs, it was calculated that current annual compensation was given by • Z = 10, 990 + 1120 x + 873 y, where x and y are number of years of work ex prior and post MBA. Find the partial derivative wrt x and y and interpret.

Higher Order Partial Derivatives • When a function depends on two variables and we desire to find the sensitivity wrt both at the same time • Derivative can be taken wrt same variable more than once also to determine the nature of the rate of change • example

Application of Differentiation • Extremal Problems – maxima and minima • Curve Sketching • Mathematical Modelling

Maxima and Minima

Maxima and Minima • Find f’(x) and solve f’(x) = 0. This value of x (say x*) is the critical point; probably maxima or minima will occur at this point. • Find f’’(x). • If f’’(x) > 0 then a minima • If f’’(x) < 0 then a minima • What if f’’(x)=0?

Maxima and Minima • • Consider the following monopolistic scenario Price, p = 400 – 2 q where q is the quantity. Average Cost c = 0. 2 q + 4 + (400/q) Calculate the profit maximizing quantity and price. What is the maximum profit? ? • In case the govt imposes a tax of $22 per unit on the monopolist, what is the new price for profit maximization?

Integration • • Anti-derivative –> Inverse of differentiation Indefinite Integral -> ò f(x)dx = F(x) + c Integration with initial conditions – example Rules of Integration

A Practical Example If the marginal revenue function for a manufacturer’s product is related to the quantity sold q as 2000 – 20 q – 3 q*q. Find the expression for the total revenue assuming that there is no revenue when no goods get sold.
