Calculus III Hughs Hallett Math 232 A B

Calculus III Hughs. Hallett Math 232 A, B Br. Joel Baumeyer Jump to first page

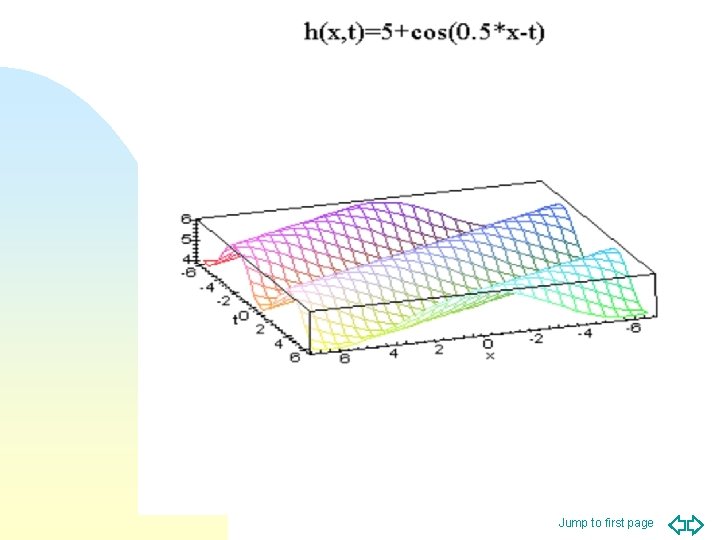
Multivariable Calculus n n n A function in Three Dimensional Space (3 -D), z = f(x, y): is a function with two independent variables; it is still a rule that assigns for each of the two independent variables, x and y, one and only one value to the dependent variable z. e. g. h(x, t) = 5 + cos(0. 5 x - t) pg 4 Jump to first page

Jump to first page

Jump to first page

3 -D Graphing Basics n n x coordinate measures the distance from the yz-plane whose name is: x = 0 y coordinate measures the distance from the xz-plane whose name is: y = 0 z coordinate measures the distance from the xy-plane whose name is: z = 0 distance: Jump to first page

Graphs of Functions in 2 Variables The graph of a function of two n n n variables, f, is the set of all points (x, y, z) such that z = f(x, y). The domain of such a function is is a subset of points in the real Euclidean plane. In general, the graph of a function of two variables is a surface in 3 -space. In particular, the graph of a linear function in 3 -space is a plane: ax + by + cz = d. Jump to first page

Section of a Graph of a Function in 3 -D n For a function f(x, y), the function we get by holding x fixed and letting y vary is called a section of f with x fixed. The graph of the section of f(x, y) with x = c is the curve, or cross-section, we get by intersecting the graph of f with the plane x = c. We define a section of f with y fixed similarly. Jump to first page

Contour Lines (or Level Curves) n n Contour lines, or level curves, are obtained from a surface by slicing it by horizontal planes. If z = f(x, y) then for some value c, where z = c, c = f(x, y) is a level curve for the function. Jump to first page

Equation of a Plane in 3 -D n n If a plane has slope m in the x direction, slope n in the y direction, and passes through the point: then its equation is: if we write: then: f(x, y) = c + mx + ny Jump to first page

Level Surfaces n A function of three variable f(x, y, z), is represented by a family of surfaces of the form: . f(x, y, z) = c, each of which is called a level surface. Jump to first page

3 -D « 4 -D n A single surface representing a two -variable function: z = f(x, y) can always be thought of a one member of the family of level surfaces representing a three variable function: G(x, y, z) = f(x, y) - z. n The graph of z = f(x, y) is the level surface of G = 0. Jump to first page

Limits and Continuity n n n The function f as a limit at the point (a, b), written: if the difference |f(x, y) - L| is as small as we wish whenever the distance from the pint (x, y) to the point (a, b) is sufficiently small, but not zero. A function f is continuous at a point if A function is continuous if it is continuous at each point of its domain Jump to first page