Calculus Date 3212014 State Championships Students out Obj

Calculus Date: 3/21/2014 State Championships Students out Obj: You need your SM and a cell phone Do Now: Evaluate definite integrals using u-substitution HW Requests: pg 342 #13, 15, #25 -43 SM 158 In class: To Do: pg 323 all HW: Complete Slope Fields Worksheet Tabledpg 361 #1 -9 odds Complete SM Announcements: Midterm next Wednesday 50 minutes Saturday Tutoring 10 -1 (Derivatives) Mock AP Exam during ACT Testing

Slope Fields Ø Ø Ø Recall that indefinite integration, or antidifferentiation, is the process of reverting a function from its derivative. In other words, if we have a derivative, the antiderivative allows us to regain the function before it was differentiated – except for the constant, constant of course. If we are given the derivative dy/dx = f ‘(x) and we solve for y (or f (x)), we are said to have found the general solution of a differential equation. For example: Let And we can easily solve this: This is the general solution:
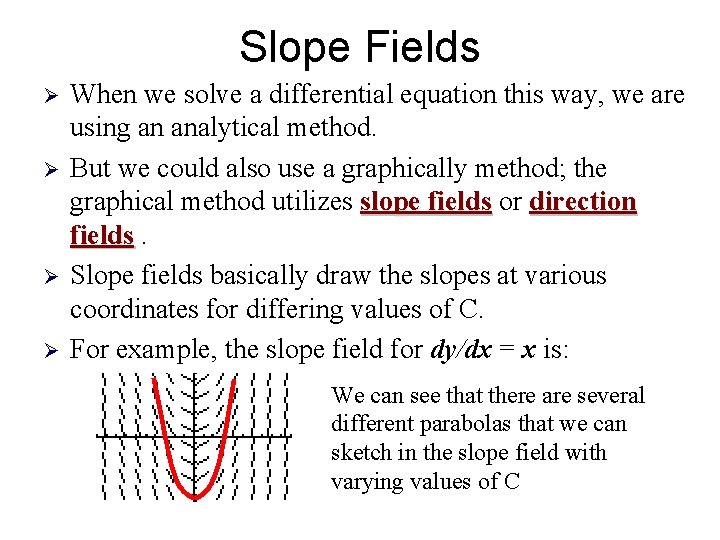
Slope Fields Ø Ø When we solve a differential equation this way, we are using an analytical method. But we could also use a graphically method; the graphical method utilizes slope fields or direction fields. Slope fields basically draw the slopes at various coordinates for differing values of C. For example, the slope field for dy/dx = x is: We can see that there are several different parabolas that we can sketch in the slope field with varying values of C

Slope Fields A slope field is a graphical picture of a derivative that projects the curve within the picture. Or a bunch of little line segments that show the slope of the curve (y = ) at different points.
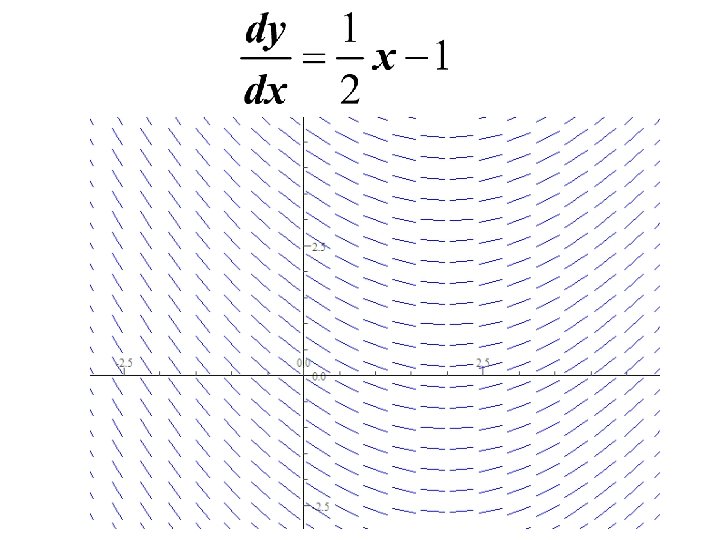
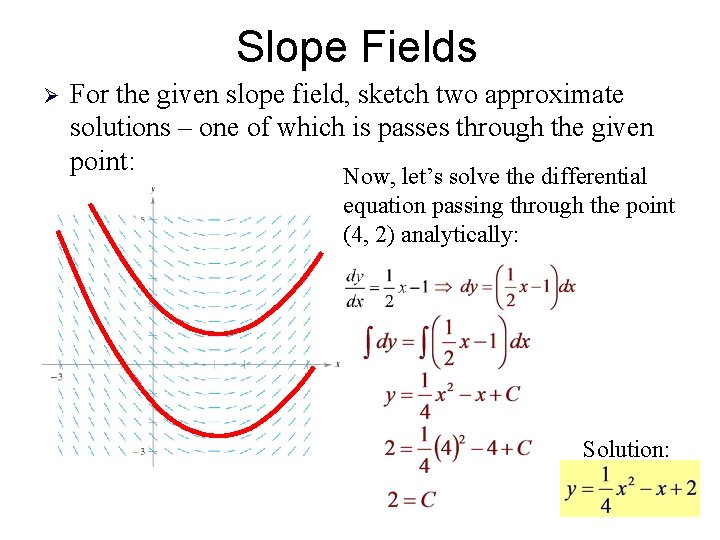
Slope Fields Ø For the given slope field, sketch two approximate solutions – one of which is passes through the given point: Now, let’s solve the differential equation passing through the point (4, 2) analytically: Solution:
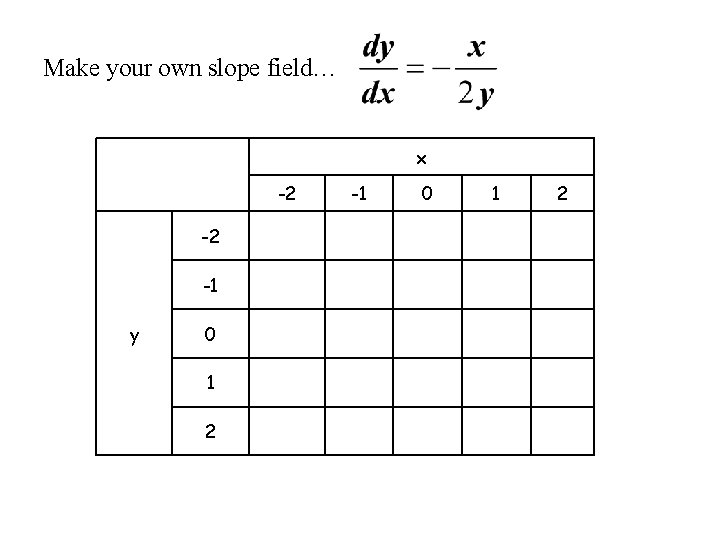
Make your own slope field… x -2 -2 -1 y 0 1 2 -1 0 1 2

How to pick out a multiple choice answer (equation) for a slope field… • pay attention to whether you need just the x- or y-values or both • Look for places where the slope is 0 • Look at the slopes along the x-axis (where y = 0) • Look for slopes along the y-axis (where x = 0) • Notice where the slopes are positive and where they are negative
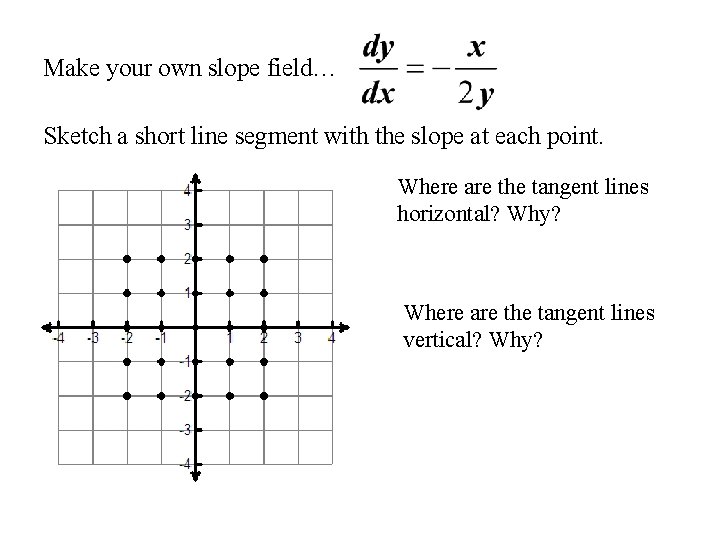
Make your own slope field… Sketch a short line segment with the slope at each point. Where are the tangent lines horizontal? Why? Where are the tangent lines vertical? Why?

Solve the differential equation to find the particular solution with initial condition y(1) = 2. Sketch the particular solution on your slope field.

End here
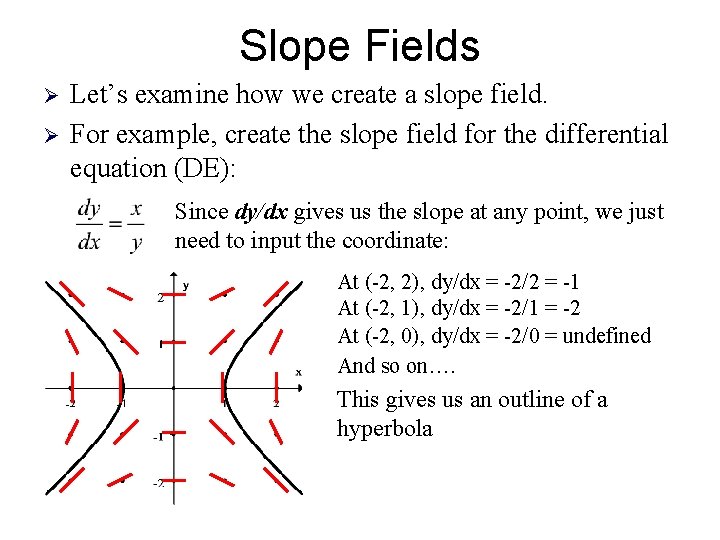
Slope Fields Ø Ø Let’s examine how we create a slope field. For example, create the slope field for the differential equation (DE): Since dy/dx gives us the slope at any point, we just need to input the coordinate: At (-2, 2), dy/dx = -2/2 = -1 At (-2, 1), dy/dx = -2/1 = -2 At (-2, 0), dy/dx = -2/0 = undefined And so on…. This gives us an outline of a hyperbola

Slope Fields Ø Let’s examine how we create a slope field. Ø For example, create the slope field for the differential equation (DE): Of course, we can also solve this differential equation analytically:

Slope Fields In order to determine a slope field Match the correct DE with its graph: A B H 1. _____ F 2. _____ 3. _____ D C E E 7. _____ B 8. _____ If isoclines (points with the same slope) are along horizontal lines, then DE depends only on y ii) Do you know a slope at a particular point? iii) If we have the same slope along vertical lines, then DE depends only on x iv) Is the slope field sinusoidal? v) What x and y values make the slope 0, 1, or undefined? vi) dy/dx = a(x ± y) has similar slopes along a diagonal. vii) Can you solve the separable DE? F G 6. _____ G i) D C 4. _____ A 5. _____ from a differential equation, we should consider the following: H

Slope Fields • Which of the following graphs could be the graph of the solution of the differential equation whose slope field is shown?
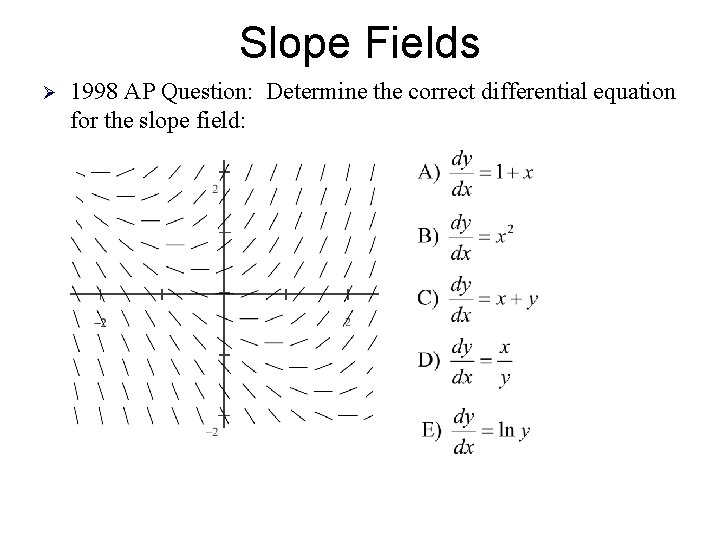
Slope Fields Ø 1998 AP Question: Determine the correct differential equation for the slope field:
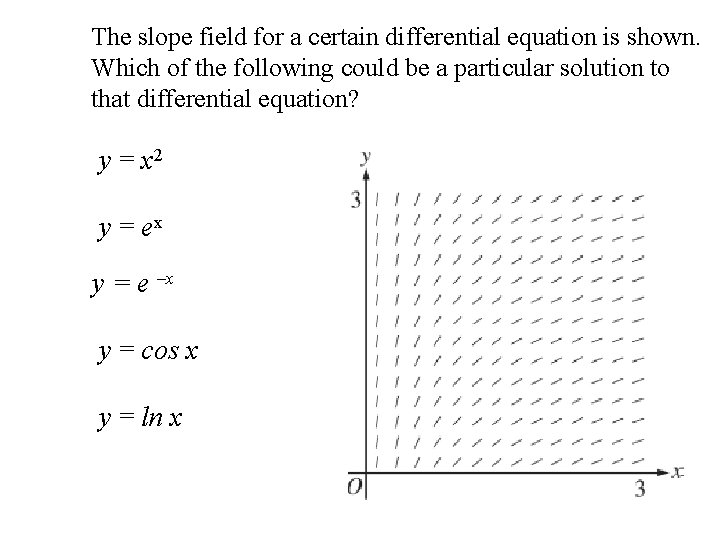
The slope field for a certain differential equation is shown. Which of the following could be a particular solution to that differential equation? y = x 2 y = ex y = e –x y = cos x y = ln x

Group Activity Make your own… Student 1 Student 3 Student 2 Student 4

• What do you notice about the slope fields whose differential equation had only x’s? • What do you notice about the slope fields whose differential equation had only y’s?

Shown is a slope field for which of the following differential equations? A) B) C) D) E)
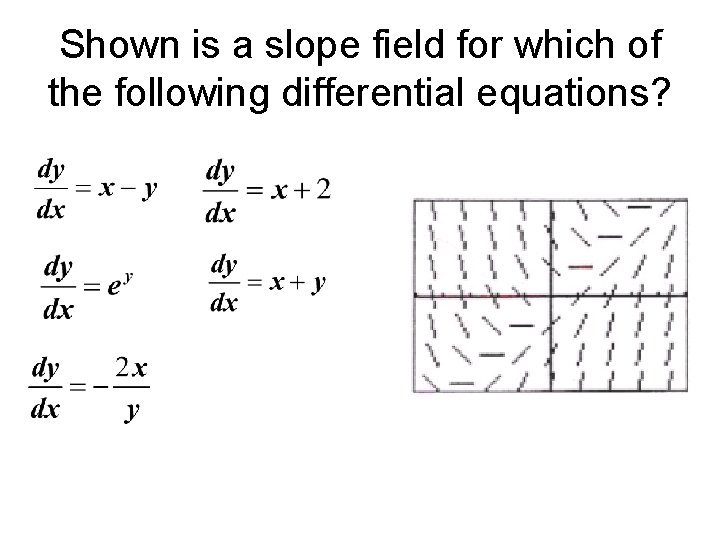
Shown is a slope field for which of the following differential equations?

Which of the following differential equations matches the slope field given?

Which of the following differential equations matches the slope field given?
- Slides: 23