Calculus Course Baseline Rendering Baseline vs Progressive Rendering

Calculus Course

Baseline Rendering

Baseline vs. Progressive Rendering 25% 50% 100%
Frank Current Garden George
Frank Current Garden George
Frank Current Garden George
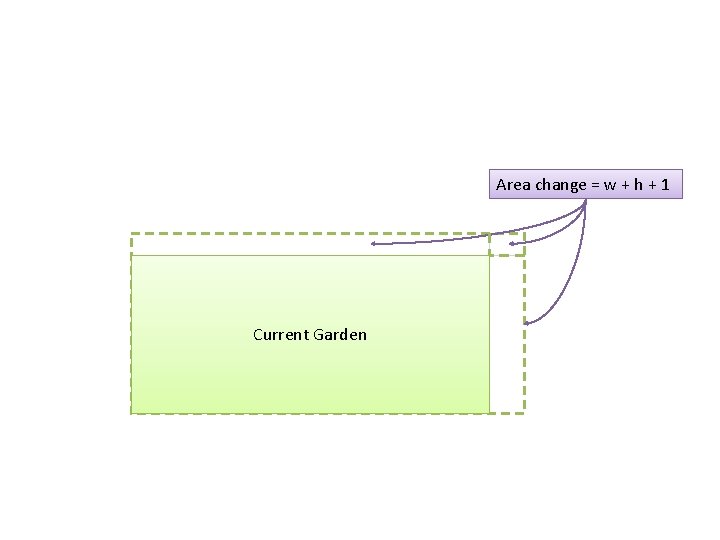
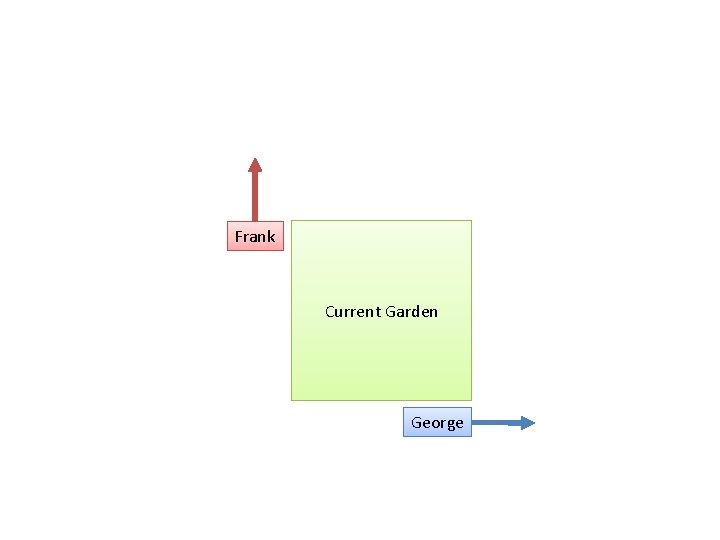
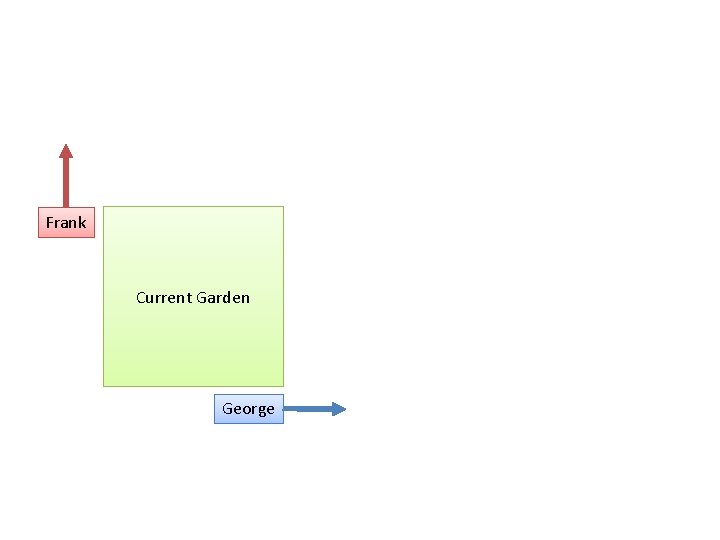
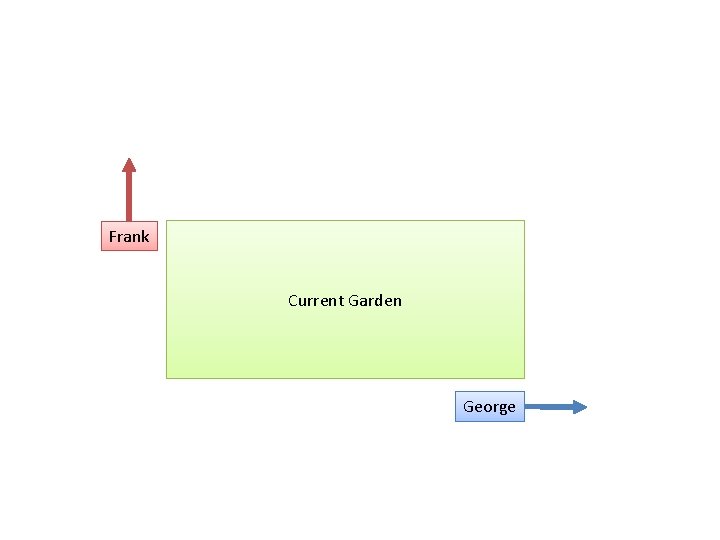
Area change = w + h + 1 Current Garden
![System Derivative A+B+C []+[]+[] A*B*C []+[]+[] A^(B^C) []+[]+[] A^B / C []+[]+[] Three inputs, System Derivative A+B+C []+[]+[] A*B*C []+[]+[] A^(B^C) []+[]+[] A^B / C []+[]+[] Three inputs,](http://slidetodoc.com/presentation_image_h/0b12f4cdcbdf0172370d77c77f0072ed/image-8.jpg)
System Derivative A+B+C []+[]+[] A*B*C []+[]+[] A^(B^C) []+[]+[] A^B / C []+[]+[] Three inputs, 3 changing perspectives to include
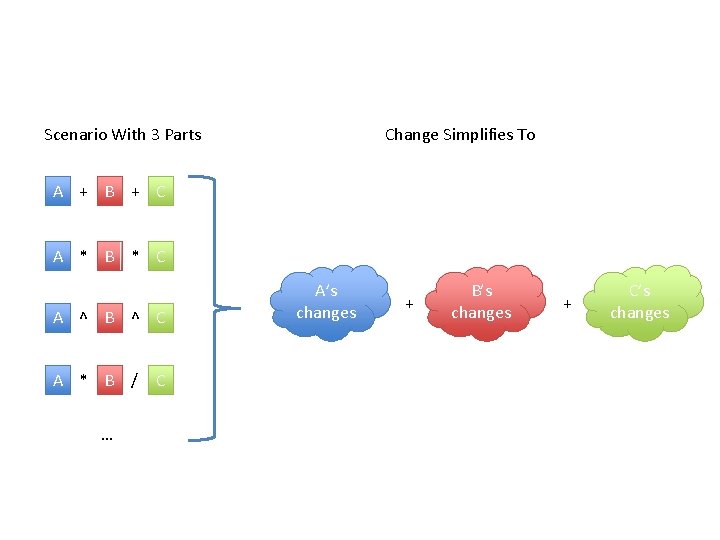
Scenario With 3 Parts Change Simplifies To A + B + C A * B * C A ^ B ^ C A * B / … C A’s changes + B’s changes + C’s changes
![System Derivative A+B+C []+[]+[] A*B*C []+[]+[] A^(B^C) []+[]+[] Three inputs, 3 changing perspectives to System Derivative A+B+C []+[]+[] A*B*C []+[]+[] A^(B^C) []+[]+[] Three inputs, 3 changing perspectives to](http://slidetodoc.com/presentation_image_h/0b12f4cdcbdf0172370d77c77f0072ed/image-10.jpg)
System Derivative A+B+C []+[]+[] A*B*C []+[]+[] A^(B^C) []+[]+[] Three inputs, 3 changing perspectives to include
![Scenario With 2 Parts System Derivative A + B A*B*C []+[]+[] A^(B^C) []+[]+[] … Scenario With 2 Parts System Derivative A + B A*B*C []+[]+[] A^(B^C) []+[]+[] …](http://slidetodoc.com/presentation_image_h/0b12f4cdcbdf0172370d77c77f0072ed/image-11.jpg)
Scenario With 2 Parts System Derivative A + B A*B*C []+[]+[] A^(B^C) []+[]+[] … Fuzzy Viewpoint Fuzzy Derivati A’s ve changes + B’s changes

Course Strategy/Content • Lesson 1: Intro • Lesson 2: Calculus In a Few Short Minutes

Lesson 3: Building A Garden – – Go through this example end-to-end Learning how to break things down step-by-step • • • – – – Seeing changes *evolve*, not just the final result Want to give an example so you can discover calculus ON YOUR OWN, for yourself. It’ll click that much better. Adding up the pieces… get a series of soil dumped your way. You know it’s making a square pattern! Tick… tick. Every tick, they take a step. Simple description • • • – Did you notice… 4 feet of perimeter added for each tick Did you notice… area went up 1, 3, 5, 7, 9, 11, 13, 15, 17, 19… and all the increases combine to the 100 square feet we now have! Imagine we get a delivery of 10 square feet of mulch every day • • • – – – Ask two friends to help set up a garden One walks North, one walks East You’re not sure how big you want it. So you ring a bell. Each time it rings, they walk 1 foot more. Clang! Way to small. Clang clang! It’s 4 x 4… still too small! Clang clang! Now it’s 8 x 8. Not bad. Clang! It’s 9 x 9. Decent, but a tad bigger would do. Clang! Now it’s 10 x 10. And your friends are glaring. After 10 ticks, we have 10 x 10 square. Perimeter 40. Area 100. Fine. But along the way • • – Why? Business person. Want to see a record of each sale and expense, or just the bank balance at the end of the month? Coach? Want to see the play-by-play summary, or just the final score? If you’re making decisions… you want to see the changes that LED to a result, not just the final result! (You can always “replay” all the changes and get the final result anyway) In the beginning, we can just make our garden At some point, we can no longer take a step forward. Once we’re at 5 x 5, the next step (to 6 x 6) will require 5*2 + 1 = 11 square feet. Ack. We have to “save up” a day. And later As long as 2*x + 1 < incoming rate. Don’t start abstracting too early. We can just notice these patterns. The problems that may arise. This is “calculus”. Calculus is putting a name to these special patterns we noticed (the derivative – how it changed along the way) Calculus is working backwards from the sequence of changes, to what pattern is being made (see 1, 3, 5, 7, 9… a square!) Calculus is optimizing what you need (what if we need to stop after we *add* 10 or more square feet of area…) Calculus is strategies for breaking a “final result” into a sequence of smaller steps

Lesson 4: Splitting a cake – Goal: Another scenario to examine step-by-step – You’re having a birthday part. About to cut the cake. • Friend comes in • And another – How do you model the changes? How much cake are you losing with each additional person? – Inverse relationship (your share is 1/x). How is your share changing as x (the number of people) increases? – So… can you see how ¼ = 1 [starting] – ½ [one person] - 1/6 [another comes in] – And 1/5 = 1 – ½ - 1/6 – 1/12 [and another] – Neat! – How many people does it take to save $50/person? (1/20 the total? ) – Calculus. Transaction-by-transcation. • You could manually start adding differences… but calculus gave you the pattern! • Where do you need to be to see the change you need ? – Would have noticed that pattern on your own?

Lesson 5: Find The Perfect Rate • Let’s dive in: time to see how to make calculations on our own. Here’s the basic process – – – • How to – – • So we get the measurement, but then make it INDEPENDENT of the size of our change (i. e. , a perfect change) We let dx go to zero. Example: Cutting our Cak – – • Current area: x^2 (i. e. , 10 x 10) New area: (x + dx)^2 (i. e. , 11 x 11) Change: 2 x. dx + dx^2 = 20*10*1 + 1^2 = 21 Change on a “per dx’ basis: 2 x + dx What do we see? One part of it depends on our current value (x) but another part ONLY depends on the change we made! (dx^2) Example: Measuring your speed. Imagine the speed measurement forced you to go a whole hour… ugh! We want to make it independent. – – • If x is our variable, then “dx” (aka delta x) is the amount it changes If we have a 10 x 10 garden and go to 11 x 11, then x =10 and dx = 11 Example: Building our Garden – – – • Come up with the change formula Find change on a per-change basis Make it perfect Note – Current: 1/x New: 1/(x + dx) Change: -1/x(x+dx) Make it perfect: -1/x^2 Limits and infinitesimals are the formal rules we use to “let dx turn to zero”.

Nested Systems

Open ended question • How can we account for the size of the change? • What does d/dx f^2 mean? – We have a system which is based on x somewhere along the line (f) – But we are going to square it – So we know the change in the outer system: 2 f + 1 – And then we multiply by df/dx, how much it then depends on x • Look at the outer system’s changes • Then drill into the inner one • Most common mistake – Getting confused about when to include the other dx – 1/g^2 … dg/dx [which could be 1!!!]

Lesson 6: Exchanging Currency • • Pretend you can get $3 in profit per square foot Make a clap… how much more profit will you get? – – • We have a chain reaction We clap, which makes area go up… Which makes profit go up… Which makes EUR go up And later – Chain reaction. Change A (how much does it change? ) which changes B (how much does it change? ) which changes C (how much does it change? ), on and on. • We have a 2 x 2 and we clap… – Which makes our area go up 5 feet (2 x + 1) – Which makes our profit go up (3) – Which could be converted • Now, let’s say our profit was not just linear… another proportion? – Clap, which is 2 x + 1 – And that is how long we run another clapper for (2 x + 1) over there!

More Chain Rule Analogies • We want the “currency” of u, v, w, etc. • x changes… which goes up the chain • Or work top-to-bottom – The outer system is based on this inner one – When this inner system changes, we SCALE IT UP [here is the confusion… the inner system is changing BY A RATE… and we are scaling up that rate] – Can we have the inner system change by a set amount? x => x + dx? • Then the outer system changes by df • df/dx = 2 x [rate it changes, on a per-dx basis] • df = 2 x. dx [actual amount it changes]

Search online for chain rule analogies… have it really click • So, the key is realizing the rates are NOT like gears (which are fixed) • The conversion rate changes! • A to X = A to B, B to C, C to D… D to X – Each step can be non-linear – Not just a number! An entire conversion – How much are we going to get? What it’s based on? • Let’s say the “A to B” step is A = B^2 • Then changing B (d. B) has the effect 2 A * d. A • So we drop in the 2 A d. A – Keep going! Now we can start to get really complex. Neat. Let’s solve some problems for real. • Giant applications of the chain rule.
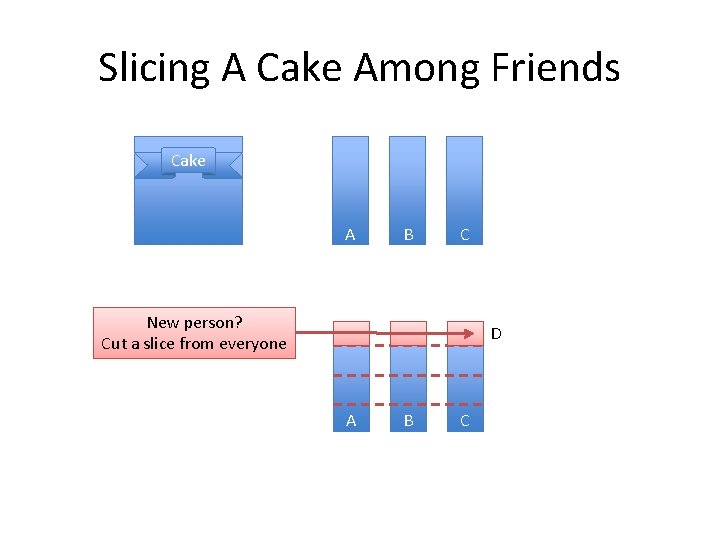
Slicing A Cake Among Friends Cake A B C New person? Cut a slice from everyone D A B C

• Lesson 5: How to find derivatives • Lesson 6: How to throw the unneeded things away
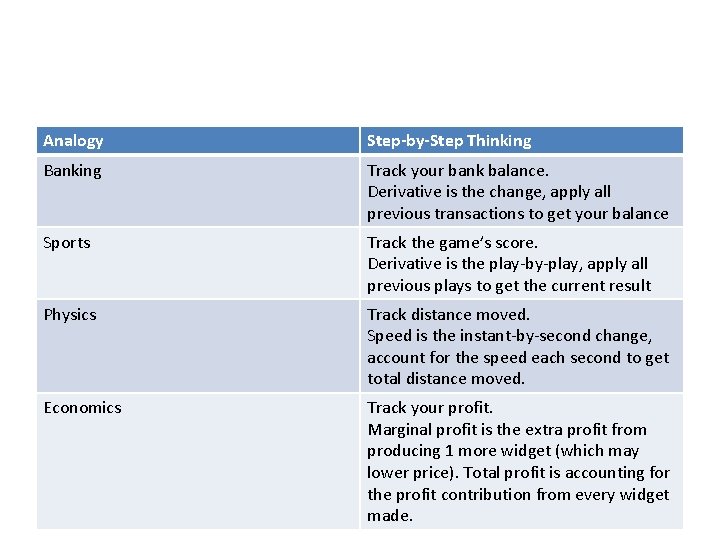
Analogy Step-by-Step Thinking Banking Track your bank balance. Derivative is the change, apply all previous transactions to get your balance Sports Track the game’s score. Derivative is the play-by-play, apply all previous plays to get the current result Physics Track distance moved. Speed is the instant-by-second change, account for the speed each second to get total distance moved. Economics Track your profit. Marginal profit is the extra profit from producing 1 more widget (which may lower price). Total profit is accounting for the profit contribution from every widget made.

Concept Goals • Want you to think step-by-step – Not just final results • Learn how to make better estimates – Go from discrete (large, noticeable steps) to continuous (perfectly smooth, undetectable steps) • Learn how to calculate the actual changes – Derivative: see what the next step will be – Integral • Mechanical: accumulate previous steps to get a total • Artistic: Figure out what shape the total is forming

Gotcha! • Remember it’s – (1/g)’ = -1/g^2 * dg/dx – We need that dg! Have to jump into the rate. We’re saying… • The scaling factor is -1/g^2 times the rate we end up moving • Don’t forget about that extra dg. Every term needs that scaling factor.

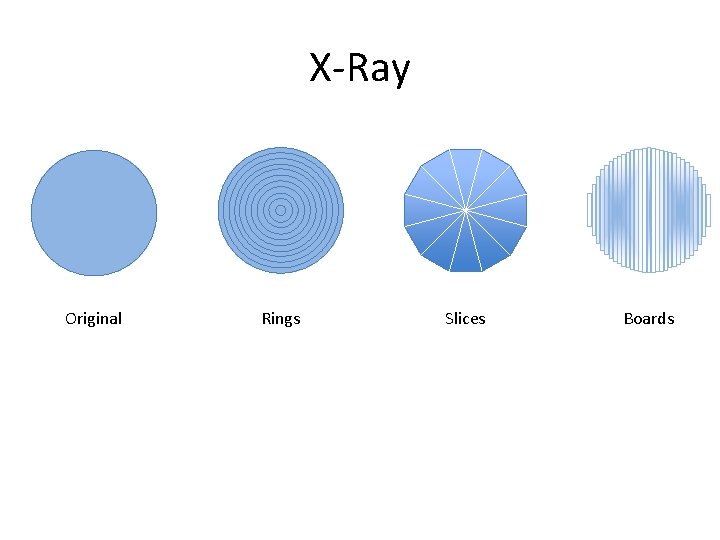
X-Ray Original Rings Slices Boards
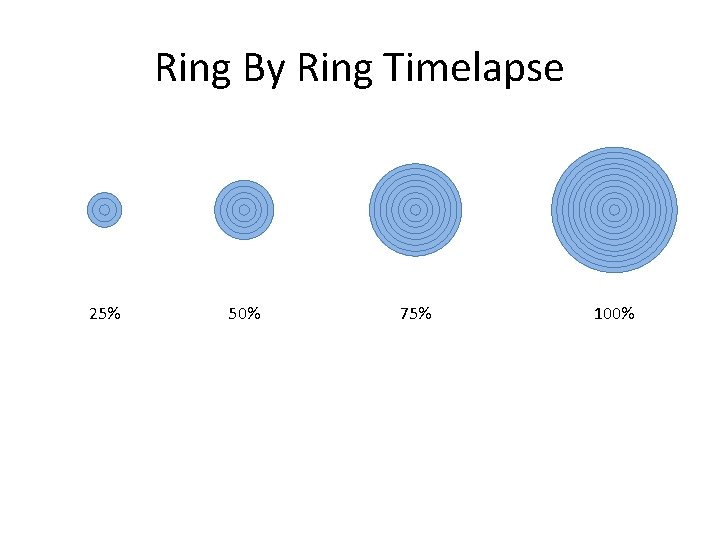
Ring By Ring Timelapse 25% 50% 75% 100%

X-Ray


Shape
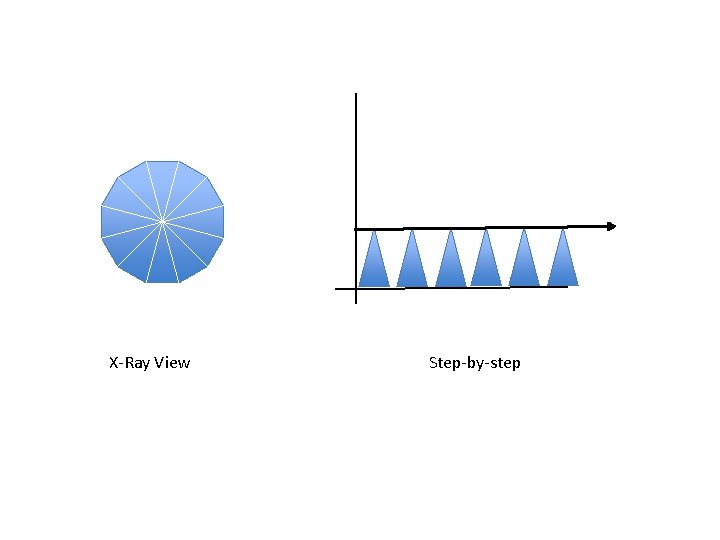
X-Ray View Step-by-step
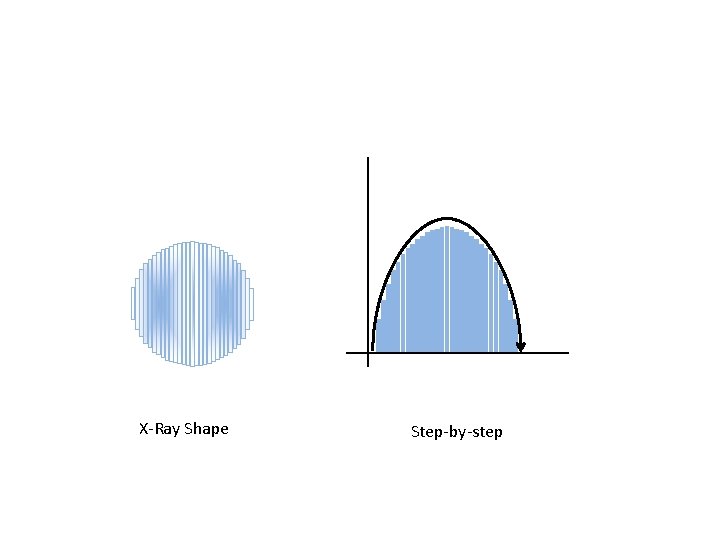
X-Ray Shape Step-by-step
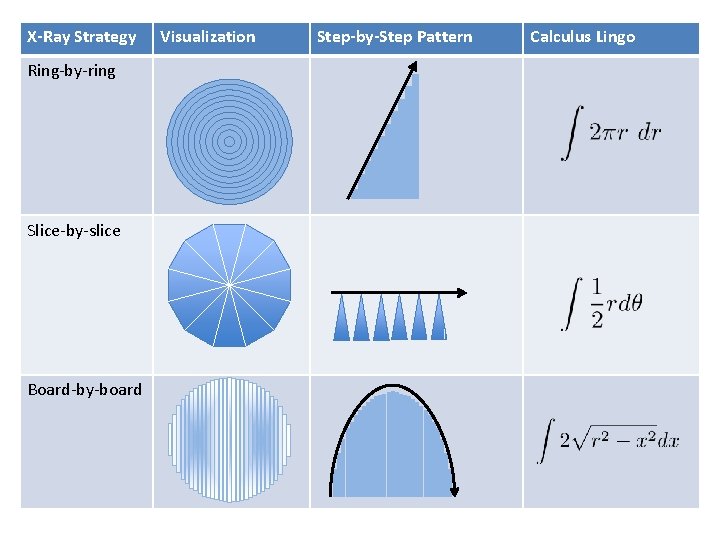
X-Ray Strategy Ring-by-ring Slice-by-slice Board-by-board Visualization Step-by-Step Pattern Calculus Lingo
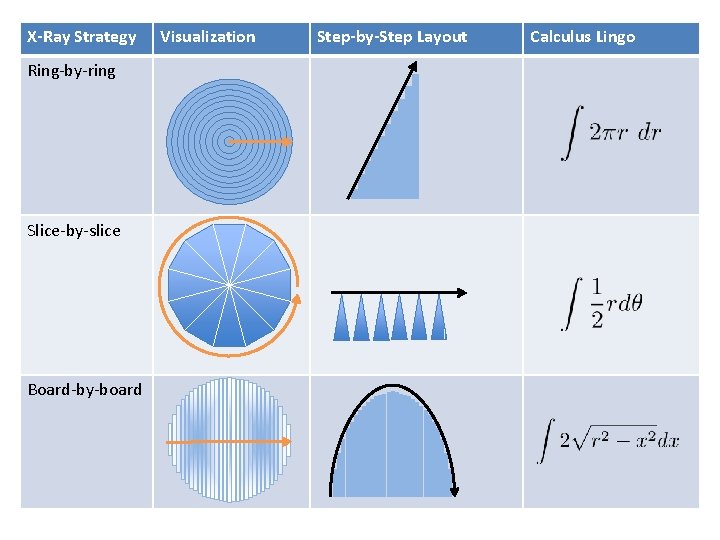
X-Ray Strategy Ring-by-ring Slice-by-slice Board-by-board Visualization Step-by-Step Layout Calculus Lingo
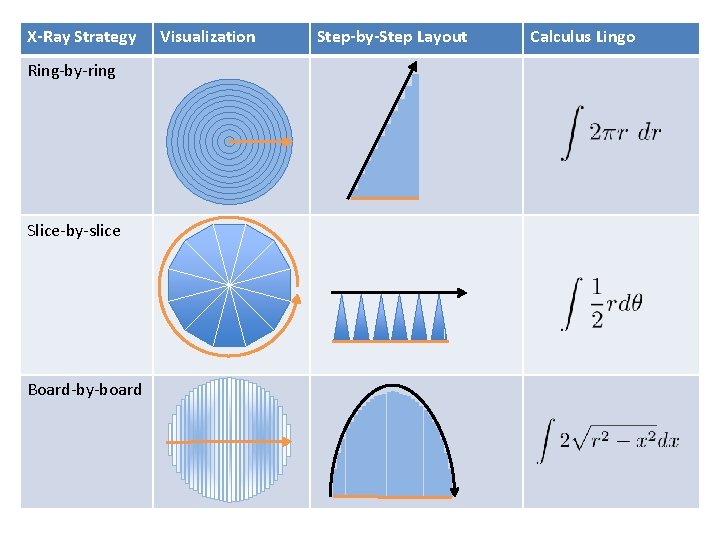
X-Ray Strategy Ring-by-ring Slice-by-slice Board-by-board Visualization Step-by-Step Layout Calculus Lingo
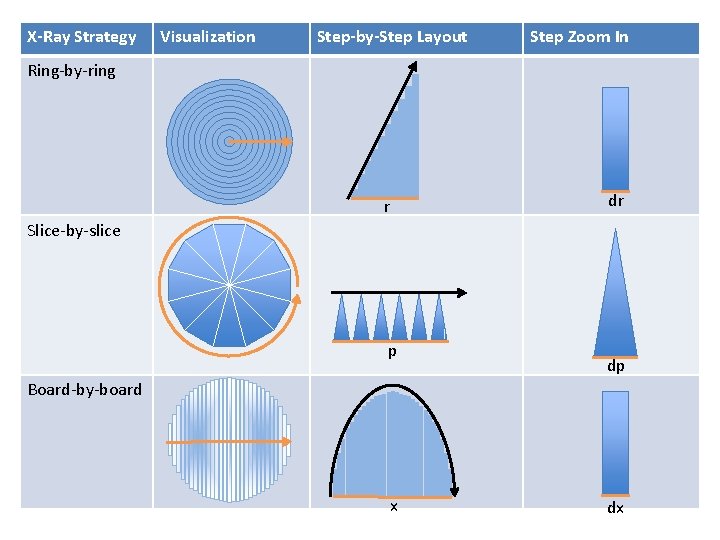
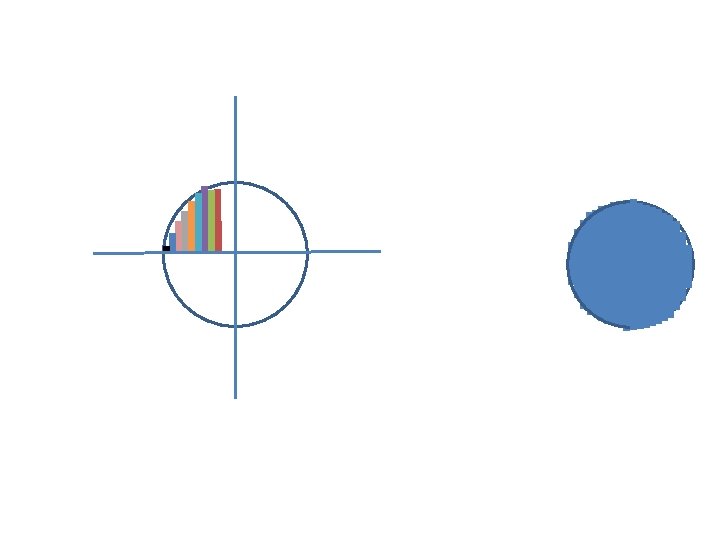
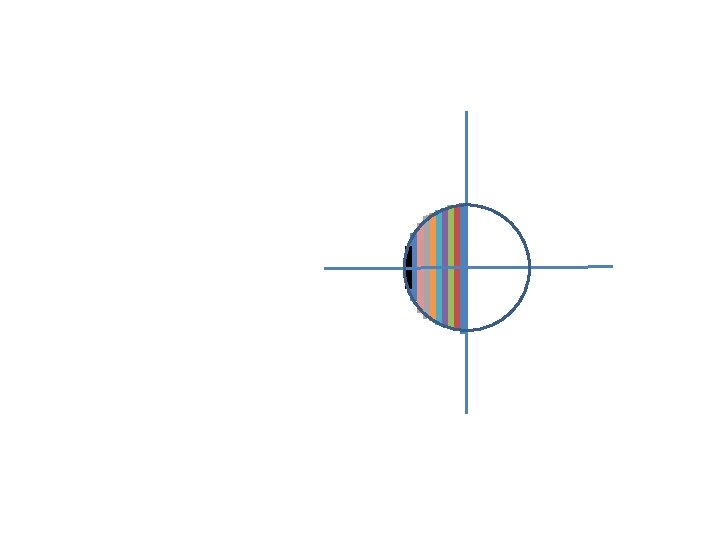
X-Ray Strategy Visualization Step-by-Step Layout Step Zoom In Ring-by-ring r dr Slice-by-slice p dp Board-by-board x dx

Shape Animation Spin



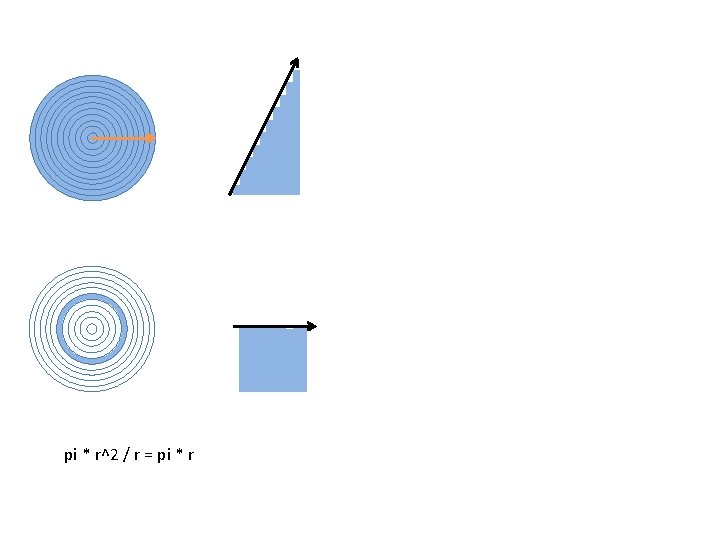
pi * r^2 / r = pi * r
- Slides: 45