Calculus Cookbook Chapter 2 Limits and Their Properties

Calculus Cookbook: Chapter 2 Limits and Their Properties

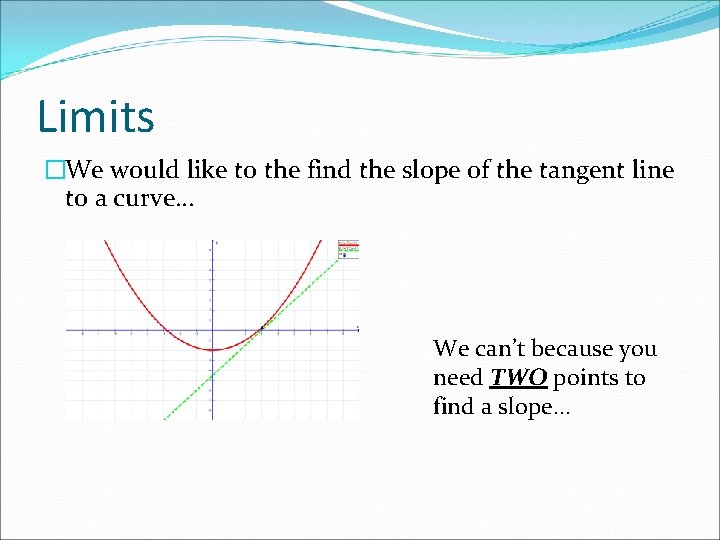
Limits �We would like to the find the slope of the tangent line to a curve… We can’t because you need TWO points to find a slope…

�Instead, we use the slope of the SECANT line because two points are available. �As the slope of the SECANT line approaches the slope of the TANGENT line, we are finding the LIMIT!

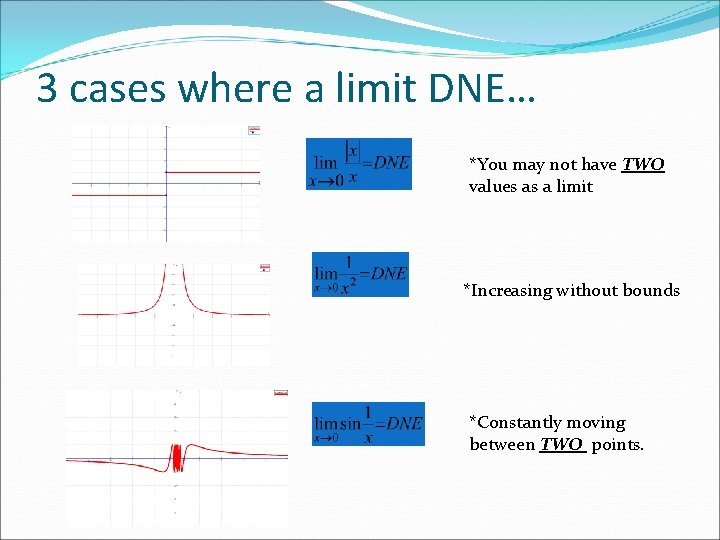
3 cases where a limit DNE… *You may not have TWO values as a limit *Increasing without bounds *Constantly moving between TWO points.

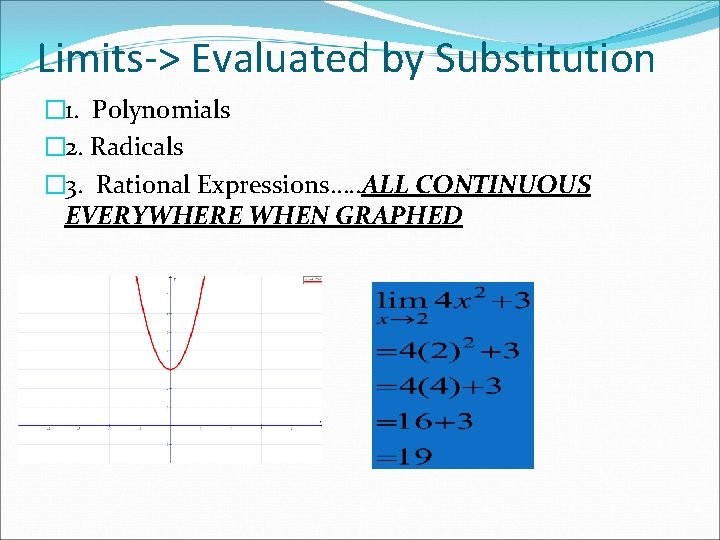
Limits-> Evaluated by Substitution � 1. Polynomials � 2. Radicals � 3. Rational Expressions…. . ALL CONTINUOUS EVERYWHERE WHEN GRAPHED

If Direct Substitution Fails… � 1. Factor, then cancel. � 2. Rationalize the numerator. �Ex:

Two Special Trig Limits… -Direct Substitution yields Undefined denominator. -Correct the limit as needed.

Continuity �A graph is continuous if… � 1. No gaps � 2. No holes � 3. No jumps

One Sided Limits �Evaluate from the LEFT and the RIGHT �Both limits MUST BE EQUAL in order for the limits to exist! **Both limits =

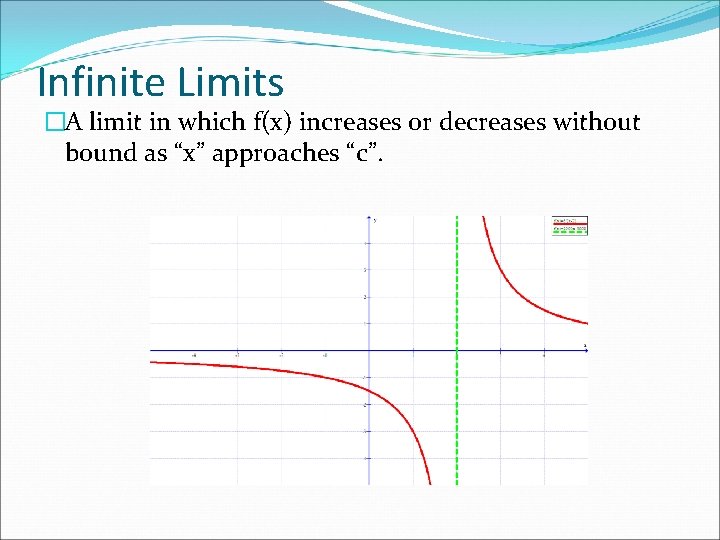
Infinite Limits �A limit in which f(x) increases or decreases without bound as “x” approaches “c”.

To Find and Asymptote � 1. Set the denominator equal to “zero” and solve � 2. Answers are where vertical asymptotes exist. �Ex: Vertical Asymptotes @ x = 4 and x = 1.

To Find Infinite Limits � 1. Factor numerator and/or denominator if possible. � 2. Cancel, if possible. � 3. With what remains: �A. Set numerator equal to zero to find x- intercepts. �B. . Set denominator equal to zero to find vertical asymptotes � 4. Select appropriate points to find designated limits.