Calculo e Instrumentos Financeiros Parte 1 Pedro Cosme

Calculo e Instrumentos Financeiros Parte 1 Pedro Cosme Costa Vieira Faculdade de Economia da Universidade do Porto 2015/2016 Actualizado no dia 08 de Outubro de 2015 1

Sexta Aula 2

Pagamento da dívida Rendas / amortizações 3

Rendas • Já consideramos duas possibilidades para o pagamento da dívida. • 1) Os juros são pagos periodicamente e o capital é pago no fim do prazo contrato. • 2) O capital mais os juros são pagos no fim do prazo contrato. 4

Rendas • Vamos explorar uma outra possibilidade • É paga uma prestação em cada período • No final do prazo não há mais nada a pagar – Cada prestação contêm juros e amortização do capital • Denominamos este plano como uma Renda 5

Rendas • Uma renda transforma uma determinada soma de dinheiro num rendimento. • Um stock num fluxo 6

Rendas • As prestações podem ser – regulares ou irregulares no tempo – constantes ou variáveis no valor – haver ou não diferimento de alguns períodos – terem duração limitada ou serem perpétua 7

Rendas • Emprestamos um capital que recuperamos na forma de uma renda – e. g. , saiu-nos a lotaria e queremos um rendimento mensal • Pedimos um capital que pagamos na forma de uma renda – e. g. , um crédito à habitação que amortizamos mensalmente 8

Rendas • Pagamos uma renda que recebemos no final na forma de um capital – e. g. , depositamos uma quantia mensal para comprar um barco a pronto no futuro • Recebemos uma renda que pagamos no fim na forma de um capital – e. g. , termos um rendimento mensal à custa de uma herança que vamos receber no futuro 9

Rendas • Receber uma renda que pagamos na forma de renda – e. g. , pagamos os estudos com um financiamento mensal que amortizamos no futuro com uma prestação mensal. 10

Rendas • Obtemos o valor actual da renda descontando todos os recebimentos ao instante de tempo presente. • Para efeito de comparação, podemos usar outro instante de tempo qualquer mas tem que ser o mesmo para todas as prestações 11

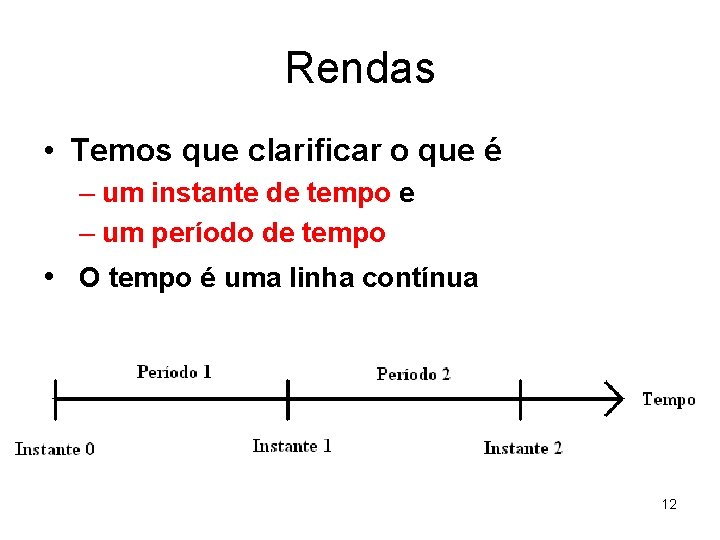
Rendas • Temos que clarificar o que é – um instante de tempo e – um período de tempo • O tempo é uma linha contínua 12

Rendas • Cada ponto é um instante de tempo – e. g. , às 12 h 00 do dia 15 de Janeiro de 2010. • Um intervalo de tempo é o segmento que medeia dois instantes de tempo, – e. g. , o semestre que medeia entre as 12 h 00 do dia 15 de Janeiro de 2010 e as 12 h 00 do dia 15 de Julho de 2010. • O instante final de um período é sempre o instante inicial do período seguinte. – e. g. o fim de 2010 é igual ao início de 2011. 13

Rendas • Ex. 1. 21. No sentido de se licenciar, um estudante necessita uma renda antecipada cuja prestação mensal é de 300€/mês e a duração de 36 meses. Supondo uma taxa de juro de 5%/ano, utilize o Excel para calcular o valor actual dessa renda 14

Rendas B 4: =B$2 C 4: =B 4*(1+B$1)^-((A 4 -1)/12) e copiava C 40: =SUM(C 2: C 37). Em vez de calcular a taxa de juro mensal, utilizei partes fraccionadas nos anos, (A 4 -1)/12. 15

Rendas • Ex. 1. 22. O Jardel, aos 26 anos de idade, ganhava 300 mil€ por mês. • Poderia ter constituído um depósito de 1. 5 milhões de euros e • Receber, a partir dos 35 anos, 600 prestações mensais de 5000€ cada. • Determine a taxa de juro implícita. 16

Rendas • • F 2: =(1+F 1)^(1/12)-1 C 2: =B 2*(1+$F$2)^-(A 2 -A$2) e copiava até C 602; F 3: =Sum(C 2: C 602). Definir F 3 para atingir o valor 0 por alteração da célula F 1. 17

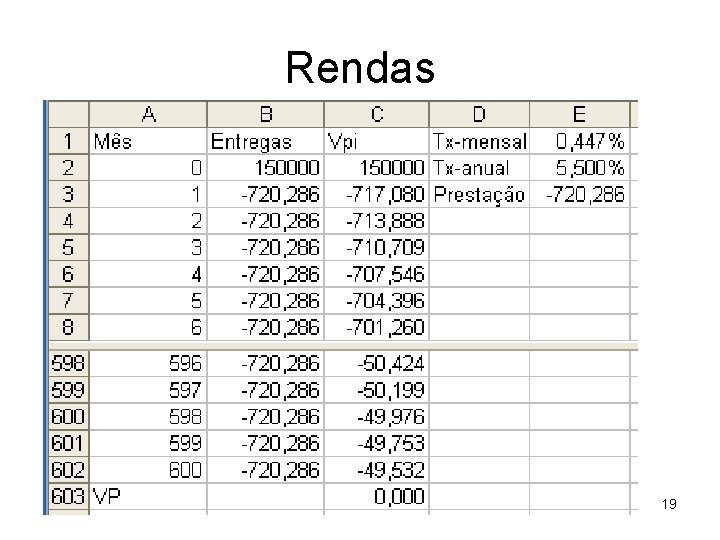
Rendas • Ex. 1. 23. Uma família adquiriu uma habitação mediante um empréstimo bancário de 150 mil€ à taxa de juro de 5. 5% anual a 50 anos. Qual a prestação mensal a pagar? 720. 29€ / mês 18

Rendas 19

Rendas • Na coluna A estão os meses, na B as quantias recebidas, na C as quantias descontadas ao presente • B 3: =E$3; C 3: =B 3/(1+$E$1)^A 3 e depois copiamos ambas em coluna. • C 603: =Sum(C 2: C 602); E 1: =(1+E 2)^(1/12)– 1. • Usava a ferramenta “atingir objectivo” definindo C 603 para 0 por alteração de E 3. 20

Rendas • Fazer em casa os dois exercícios anteriores com uma conta corrente 21

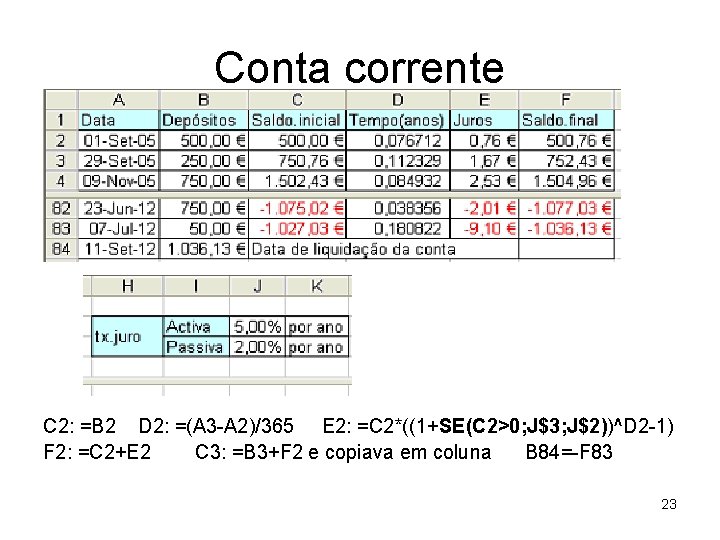
Conta corrente • Ex. 1. 25. Uns comerciantes de frutas e legumes numas alturas podem poupar e noutras não. Como, em média, conseguem poupar 325€/mês, quando o filho fez 15 anos, pensando que precisará de 750€/mês quando for para a universidade, decidiram constituir uma conta poupança. • Numa folha de Excel lancei a data e os movimentos (colunas A e B). • A taxa de juro quando o saldo é negativo (taxa de juro activa) é de 5%/ano e quando os saldo é positivo (taxa de juro passiva) é de 2%/ano. 22

Conta corrente C 2: =B 2 D 2: =(A 3 -A 2)/365 E 2: =C 2*((1+SE(C 2>0; J$3; J$2))^D 2 -1) F 2: =C 2+E 2 C 3: =B 3+F 2 e copiava em coluna B 84=-F 83 23

Sétima Aula 8 Out 24

Expressão analítica de uma renda 25

Renda perpétua • Numa renda perpétua, prestação para sempre. recebe-se uma • Sendo a taxa de juro i e os recebimentos no fim de cada período (i. e. , postecipada), é uma situação idêntica a um depósito em que no fim de cada período, são pagos apenas os juros 26

Renda perpétua postecipada 27

Renda perpétua • Como os juros de cada período valeriam J = V i Com P e i podemos determinar o valor da renda (ou da taxa de juro implícita com P e V) P = prestação, i = tx. juro, V = valor actual da renda 28

Renda perpétua • Ex. 1. 26. Um agricultor arrendou um terreno por 50€/mês para sempre. Supondo uma taxa de juro de 5% ao ano, qual será o valor presente do terreno? 29

Renda perpétua • Primeiro, calculo a taxa de juro mensal • i. mensal = (1+5%)^(1/12)-1 = 0. 407% • Depois, aplico a expressão • V = 50 / 0. 407% = 12278. 58€ 30

Renda perpétua • Ex. 1. 27. Um eucaliptal produz, a cada 10 anos, 12 kg/m 2 de madeira. Supondo um preço de 0. 03€/kg de madeira e uma taxa de juro de 3%/ano, qual será o valor actual do eucaliptal? 31

Renda perpétua • R. Calculo a taxa de juro por 10 anos, (1+3%)^10– 1= 34. 392%, e aplico essa taxa na expressão da renda perpétua postecipada: • V = (12 0. 03)/34. 392% = 1. 05€/m 2. 32

Renda perpétua • Se a renda for antecipada (a prestação é paga no princípio do período), teremos que somar uma prestação inicial 33

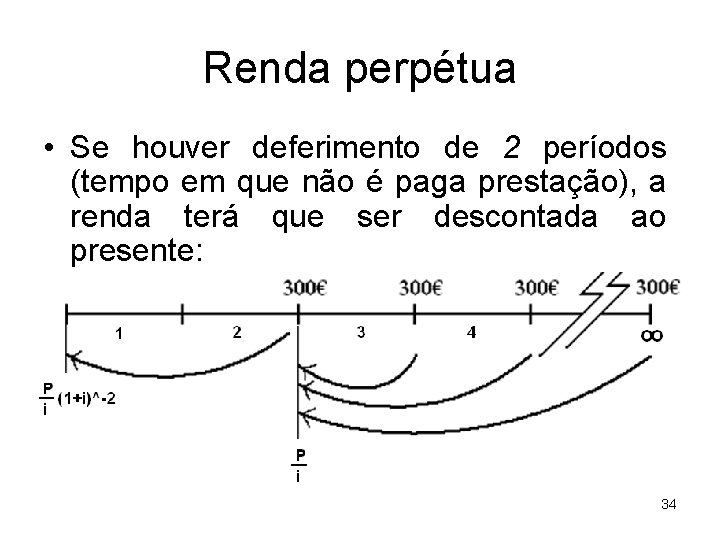
Renda perpétua • Se houver deferimento de 2 períodos (tempo em que não é paga prestação), a renda terá que ser descontada ao presente: 34

Renda perpétua • Se houver diferimento de n períodos (tempo em que não é paga prestação), a renda terá que ser descontada n períodos ao presente: • Só se começa a receber daqui a n+1 períodos (a expressão p/i é a renda postecipada) 35

Renda perpétua • Se a renda for antecipada, aplica-se a correcção: • Começa-se a receber daqui a n períodos – A renda antecipada diferida 5 anos é uma renda postecipada diferida 4 anos (estava errado, Daniel) 36

Renda de duração limitada 37

Renda de duração limitada • Com o conhecimento da expressão da renda perpétua – Também se chama perpetuidade • Podemos calcular o valor de uma renda de duração limitada • Compondo duas rendas perpétuas: uma a somar e outra a subtrair 38

Renda de duração limitada • Recebemos a prestação R entre o presente e o período N (postecipada). • É equivalente a receber uma renda perpétua a começar agora e • pagar uma renda perpétua a começar no período N, • Descontado tudo ao presente. 39

Renda de duração limitada Se a renda for paga no princípio do período (i. e. , antecipada)? Teremos que somar uma parcela. Descontar menos um período 40

Renda de duração limitada 41

Renda de duração limitada • Ex. 1. 30. Um agricultor arrendou um terreno por 50€/mês, pago no fim do mês, até que o TGV lhe destrua o terreno (i. e. , daqui a 25 anos). Supondo uma taxa de juro anual de 5%, qual será o valor presente do terreno? 42

Renda de duração limitada • Já não preciso do Excel r = (1+5%)^(1/12)-1 = 0. 407% V = 50/0. 407% x (1 – 1. 00407– 300) = 12278. 58€ x 0. 7047 = 8648. 45€ • Mas podemos usá-lo para verificar 43

Renda de duração limitada • Verificar em casa o resultado com o uso do Excel 44

Renda de duração limitada C 2: =B 2*(1+$D$2)^-A 2 C 302=sum(C 2: C 301) 45

Renda de duração limitada • Ex. 1. 29. Uma obrigação com o valor nominal de 100€ paga trimestralmente 1€ de cupão e o par (i. e. , os 100€) mais o cupão do trimestre final ao fim de 10 anos. Determine a taxa de juro desta obrigação. 46

Renda de duração limitada R. No trimestre final recebemos não só o cupão mas também o par, logo Simplificando a expressão 47

Renda de duração limitada R. Resulta i. t = 1%/trim i. a = (1 + 1%)^4 -1 = 4. 06%/ano 48

Oitava Aula 13 Out 49

Renda de duração limitada • Ex. 1. 31. o Figo, entre os 25 e os 35 anos, depositou 100 mil€/mês (i. e. , 120 prestações). • Com essa poupança vai receber uma renda de valor fixo entre os 35 anos e os 85 anos (600 prestações). • Para uma taxa de juro anual de 3%, quanto vai receber por mês? 50

Renda de duração limitada • Vamos usar como instante de referência os 25 anos (acabados de fazer) • Vamos somar – Duas rendas de duração limitada – Ou quadro rendas perpétuas Nota: Sem perda, vou usar anos para descontar e meses para a renda 51

Renda de duração limitada 52

Obrigações de taxa fixa 53

Obrigações a taxa fixa • Já foi referido que uma obrigação consiste num activo que condensa uma entrega inicial e recebimentos futuro. • Recebe-se o “cupão” ao longo do tempo e uma soma no final (o valor de remissão) • O valor da obrigação é o valor actual dos recebimentos futuros – Altera-se com o decorrer do tempo e da tx. jr de mercado 54

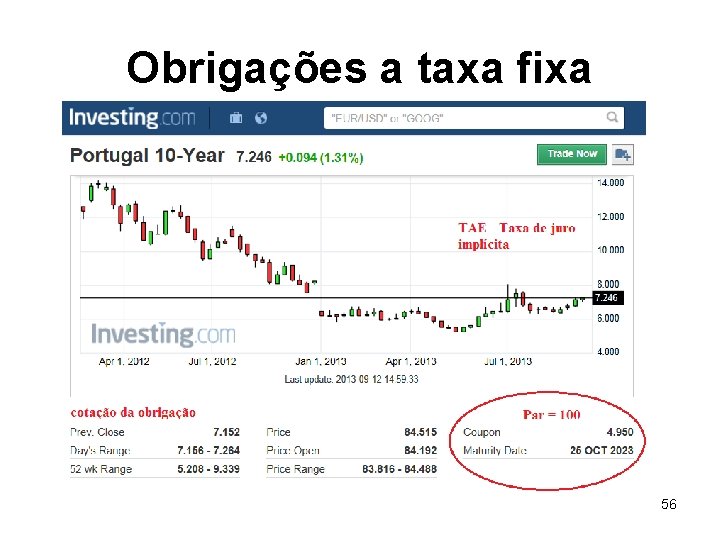
Obrigações a taxa fixa • Como valor da obrigação é o valor actual dos recebimentos futuros, • O seu valor altera-se com o decorrer do tempo – Porque se aproxima a data de remissão – Porque a taxa de juro de mercado altera-se 55

Obrigações a taxa fixa 56

Obrigações a taxa fixa • Ex. 1. 33. Uma obrigação a 10 anos de valor nominal de 100€ reembolsável ao par (i. e. , serão pagos 100€ daqui a 10 anos) cupão zero, vai ser vendida em leilão. • 1) Para uma remunerado a uma taxa média de 7. 5%/ano, qual o preço máximo que o investidor está disponível a pagar? 57

Obrigações a taxa fixa • 1) Vamos descontar os 100€ ao presente: 58

Obrigações a taxa fixa • 2) Passados 5 anos, qual será o valor da obrigação? • 3) Se o mercado justificar um aumento da taxa de juro em um ponto percentual, qual a desvalorização da obrigação? 59

Obrigações a taxa fixa • 2) Já só faltam 5 anos para receber os 100€ • 3) O aumento da taxa de juro desvaloriza a obrigação em 4. 5% 60

Obrigações a taxa fixa • 4) Se o investidor adquiriu a obrigação a 45€, qual a taxa de juro que pensava receber? • 5) E qual será se vender a obrigação depois da desvalorização? 61

Obrigações a taxa fixa • 4) A taxa de juro prevista era • 5) E passou a ser 62

Obrigações a taxa fixa • Ex. 1. 34. Uma obrigação soberana (i. e. , emitida por um Estado) a 50 anos emitida em 2010 cujo par é 1000€ paga um cupão anual de 25€ postecipado e o par mais o cupão no fim do prazo. • Qual a taxa de juro da obrigação se for adquirida ao par? 63

Obrigações a taxa fixa • Podemos simplificar a expressão obtendo uma renda perpétua: 64

Obrigações a taxa fixa • Decorridos 6 meses, no mercado secundário a obrigação está a ser transaccionada a 900€ • Para que taxa de juro aumentou a remuneração desta obrigação? – > De 2, 500%/ano para 2, 933%/ano 65

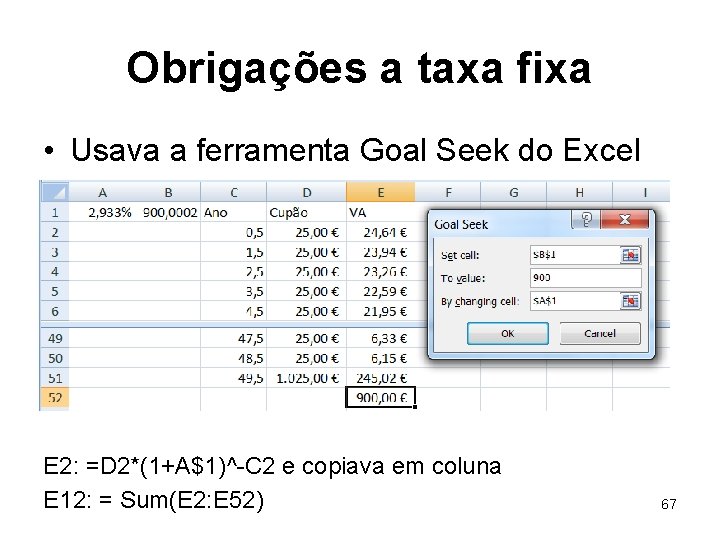
Obrigações a taxa fixa • Usava a ferramenta Goal Seek do Excel B 1. =(25/A 1*(1 -(1+A 1)^-50)+1000*(1+A 1)^50)*(1+A 1)^0, 5 Fazer B 1 = 0 pela alteração de A 1 66

Obrigações a taxa fixa • Usava a ferramenta Goal Seek do Excel E 2: =D 2*(1+A$1)^-C 2 e copiava em coluna E 12: = Sum(E 2: E 52) 67

Nona Aula 21 Out 68

TAEG Taxa Anual Efectiva Global 69

TAEG implícita no contrato • TAEG – Taxa anual efectiva global • Actualmente, é obrigatório nos anúncios (de venda a crédito) que seja afixado o preço a pronto pagamento e a taxa de juro implícita efectiva calculada com todas as despesas a incorrer pelo cliente (global) – Também é referido o total de encargos do cliente 70

TAEG implícita no contrato • A TAEG é a taxa de juro anual que faz a soma do valor actual de todos os pagamentos igual ao preço de pronto pagamento. 71

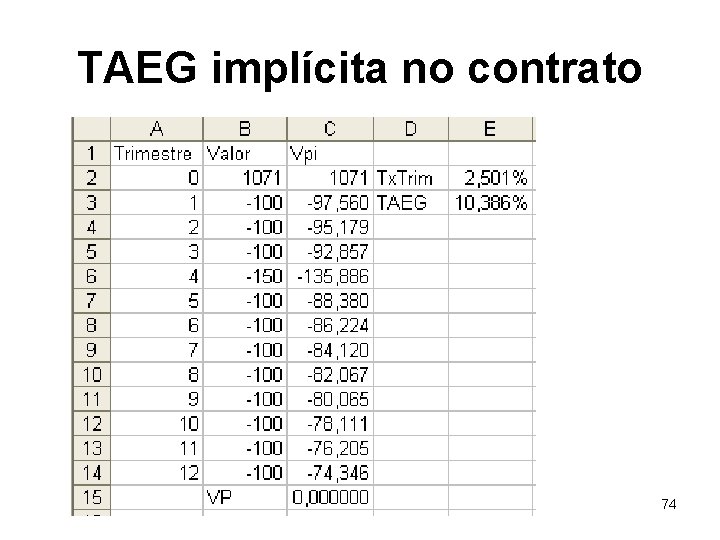
TAEG implícita no contrato • Ex. 1. 35. Um televisor (ppp de 1190€), a crédito “paga na entrega 119€ mais 12 prestações trimestrais de 100€. Tem que pagar no fim do primeiro ano mais 50€”. • Determine a TAEG deste contrato de crédito. 72

TAEG implícita no contrato • Podemos indicar algebricamente o resultado • Mas o mais fácil é determina-lo no Excel 73

TAEG implícita no contrato 74

TAEG implícita no contrato B 2: = 1190 -119; B 3: 100; B 6: -150 C 2: =B 2*(1+E$2)^(-A 2) e copiar em coluna. C 15: =Sum(C 2: C 14) Definimos a célula C 15 para o valor 0 alterando E 2. • Se a EURIBOR for 5. 5%/ano, qual é a probabilidade de incumprimento implícita neste contrato de crédito? 75

TAEG implícita no contrato 76

TAEG implícita no contrato • Ex. 1. 36. Um anúncio dizia “Telefone que lhe emprestamos 5000€ por apenas 150€ mensais (durante 60 meses, TAEG=29. 28%)”. • Confirme a TAEG. 77

TAEG implícita no contrato Tem que se determinar no Excel 78

TAEG implícita no contrato 79

Eercícios a dar caso haja tempo 80

Mistura de rendas • No dia 1/1/2000, uma pessoa abriu uma conta com 1000€ e, depois, no meio de cada mês dos trimestres 1º, 2. º e 4. º depositou 100€ e do 3º trimestre levantou 250€. • Sabendo que isto aconteceu durante 10 anos, determine para uma TAE de 2, 5% por ano qual o saldo da conta. 81

Mistura de rendas • Tenho 1000€ • Somo o VA de uma mensalidade de 100€ durante 10 anos • rm =(1+2, 5%)^(1/12)-1=0, 205984% • =100/0, 205984% *(1 -(1+0, 205984%)^120)*(1+0, 205984%)^0, 5 • 10. 633, 22 € 82

Mistura de rendas • Como somei todos os meses vou retirar 3 prestações anuais de 350€ • =350/2, 5% *(1 -(1+2, 5%)^-10)*(1+2, 5%)^0, 5 • 3098, 09 € • Julho -3. 101, 28 € *(1+2, 5%)^(5, 5/12) • 3139, 80 € • Agosto -3. 101, 28 € *(1+2, 5%)^(4, 5/12) • 3091, 72 € 83

Mistura de rendas • Como somei todos os meses vou retirar 3 prestações anuais de 350€ • Setembro -3101, 28 € *(1+2, 5%)^(3, 5/12) • 3085, 36 € 84

Mistura de rendas • • Somando tudo 1000€ 10. 633, 22 € - 3098, 09 € - 3091, 72 € - 3085, 36 € Resulta 2. 347, 11 que vou capitalizar =2. 347, 11 *(1+2, 5%)^10 =3004, 50€ 85

Obrigações perpétuas • No caso da obrigação perpétua, existe cupão, valor e remissão mas não existe prazo para a remissão. – Contam como capital próprio => Têm mais garantias que o capital social mas menos que as obrigações “normais” • Este instrumento é usado para – Reforçar o capital próprio sem diluir os direitos de voto – Construir plano de pagamento flexíveis 86

Obrigações perpétuas • O direitos de voto permitem aos accionistas decidir a governação da empresa • Constroem-se planos de pagamento flexíveis sorteando o pagamentos 87

Obrigações perpétuas • Uma empresa com capital de 10000€ precisa reforçar o capital próprio para 25000€ para o qual o sócios não têm disponibilidade. • Emitiram 1500 obrigações perpétuas (numeradas de 1 a 15000 ) com 10€ de par e um cupão anual de 15%. • Vão ser remidas 10% das obrigações por ano por sorteio do número. 88

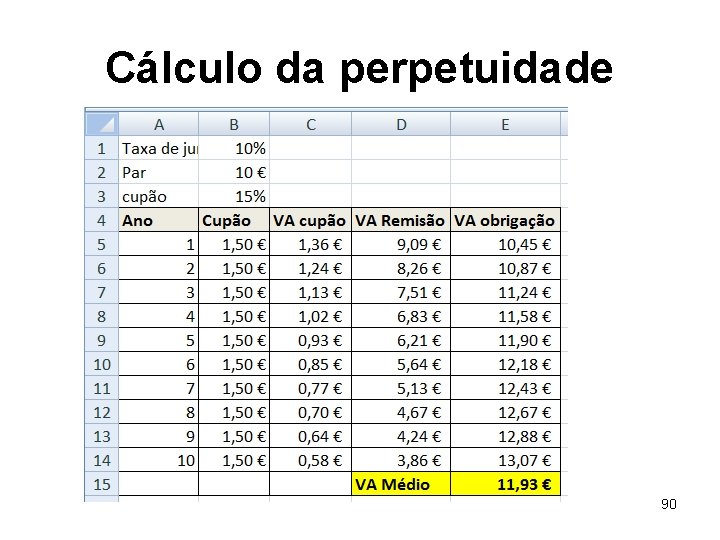
Cálculo da perpetuidade • Se fosse uma perpetuidade, se a taxa de juro de mercado para uma empresa deste tipo fosse de 10%, teríamos • VA = 1, 5/10% = 15€. • Mas a obrigação não vai durar tempo infinito. No máximo, dura 10 anos. • Temos que calcular o 10 casos e fazer a média 89

Cálculo da perpetuidade 90

Cálculo da perpetuidade • No caso, o valor médio é 11, 93€ – O “prémio” de subscrição é de 1, 93€ • • • B 5: =$B$2*$B$3 C 5: =B 5*(1+$B$1)^-A 5 D 5: =$B$2*(1+$B$1)^-A 5 E 5: =SUM(C 5: $C$5)+D 5 E copiava até à linha 14 E 15: =AVERAGE(E 5: E 14) 91

Troca de obrigações • Uma empresa emitiu em 1/1/2010 obrigações a 10 anos com par e 100€, cupão semestral postecipado de 4€, data em que a taxa de juro de mercado para empresas semelhantes era de 10%/ano. • i) Determine por quanto devem ter sido vendidas as obrigações 92

Troca de obrigações • B 1 = (1+10%)^0, 5 -1 = 4, 880885% • B 2 =4/B 1*(1 -(1+B 1)^-20)+100*(1+B 1)^-20 = 88, 91 € • São 20 semestres 93

Troca de obrigações • No dia 1/7/2015 a empresa realizou uma operação de troca em que deu uma obrigação a 10 anos com cupão semestral de 6€ em troca da obrigação que se vence em 31/12/2020. • ii) Supondo que nesse dia a taxa de juro para empresas semelhantes era de 8%/ano, qual deve ter sido o valor de remissão da nova obrigação 94

Troca de obrigações • Tenho que igualar o valor das duas obrigações. • Obrigação antiga • B 1: = (1+8%)^0, 5 -1 = 4, 880885% • Agora temos 11 semestres • B 2: = 4/rt*(1 -(1+rt)^-11)+ 100*(1+B 1)^-11 = 100, 68 € – Valorizou 95

Troca de obrigações • Obrigação nova • Agora temos 20 semestres • 6/rt*(1 -(1+rt)^-20) + X*(1+B 1)^-20 = 100, 68 € • X= (100, 68 € - 6/rt*(1 -(1+rt)^-20) )/ *(1+B 1)^-20 • = 40, 11 € 96