Calculations with Chemical Formulas and Equations Topics Featured

Calculations with Chemical Formulas and Equations

Topics Featured Mass-Mole Relationship Percent Composition Empirical Formulas Molecular Formulas Stoichiometry: Limiting Reagents Theoretical Yield Actual Yield Percent Yield Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 2

Formula Masses The mass of a carbon atom allows one to determine how many carbon atoms are present in one diamond. 1 x 1021 atoms © Foto Kormann/zefa/Corbis Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 3

Formula Masses ← Fig. 6. 1 Oranges may be bought in units of mass or units of amount. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 4

Formula Masses → Fig. 6. 2 A basic process in chemical laboratory work is determining the mass of a substance. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 5

Mass and Moles of a Substance • Chemistry requires a method for determining the numbers of molecules in a given mass of a substance. – This allows the chemist to carry out “recipes” for compounds based on the relative numbers of atoms involved. – The calculation involving the quantities of reactants and products in a chemical equation is called stoichiometry. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 6

Molecular Weight and Formula Weight • The molecular weight of a substance is the sum of the atomic weights of all the atoms in a molecule of the substance. – For, example, a molecule of H 2 O contains 2 hydrogen atoms (1. 0 amu x 2 atoms), and 1 oxygen atom (16. 0 amu), giving a molecular weight of 18. 0 amu. One molecule of water weighs: 2 (1 amu) + 16 amu = 18 amu Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 7

Molecular Weight and Formula Weight • The formula weight is the sum of the atomic weights of all the atoms in one formula unit of the compound. – For example, one formula unit of Na. Cl contains 1 sodium atom (23. 0 amu) and one chlorine atom (35. 5 amu), giving a formula weight of 58. 5 amu. One molecule of Na. Cl weighs: 23 amu + 35. 5 amu = 58. 5 amu Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 8

Example • Calculate the mass of a sample that contains 23 nitrogen atoms. 1 N atom weighs 14 amu’s Thus, 23 x 14 amu = 322 amu Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 9

Example #2 • How many sodium atoms are there in 1174. 49 amu’s? Since 1 sodium atom weighs 22. 99 amu 1174. 49 amu 22. 99 amu/Na atom Copyright © Houghton Mifflin Company. All rights reserved. = 51. 00 Na atoms Presentation of Lecture Outlines, 3– 10

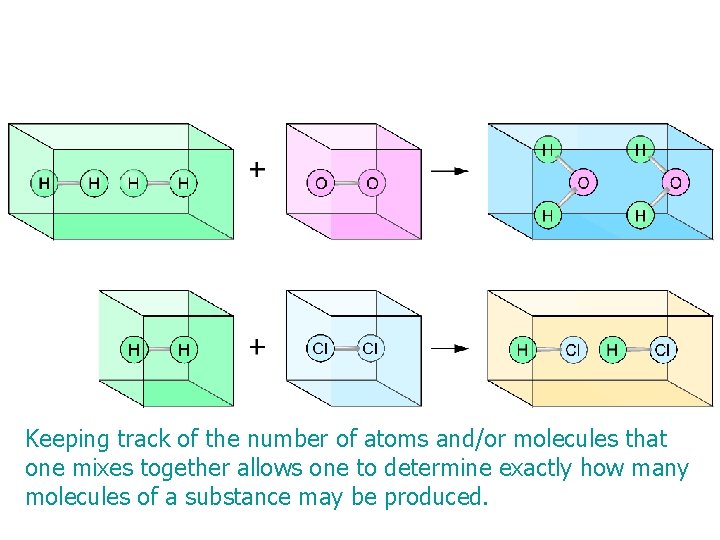
Keeping track of the number of atoms and/or molecules that one mixes together allows one to determine exactly how many molecules of a substance may be produced. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 11

Calculations: Formula Masses, Moles, and Chemical Equations cont’d Edgar Fahs Smith Collection, University of Pennsylvania → Fig. 6. 4 Amadeo Avogadro was the first scientist to distinguish between atoms and molecules. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 12

Atomic and Molecular Masses • Atomic mass - the average mass of an atom C = 12. 01 amu • Molecular mass - the average mass of a molecule CHCl 3 = 1 C + 1 H + 3 Cl = [1(12) + 1(1) + 3(35. 5)] amu = 119. 5 amu However, 1 amu = 1. 66 x 10 -24 g ; pg 206 or, 6. 022 x 1023 amu = 1 g Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 13

The Mole • The number of carbon atoms in exactly 12 grams of pure 12 C. • 1 mole of anything = 6. 022 ´ 1023 units of that thing Thus, 6. 022 x 1023 amu = 1. 00 gram 1 mole of H 2 O weighs 18. 0 grams and 1 mole of Na. Cl weighs 58. 5 grams Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 14

Avogadro’s number equals 6. 022 ´ 1023 units (denoted as “NA”)

Molar Mass • A substance’s molar mass (molecular weight) is the mass in grams of one mole of the compound. CO 2 = 44. 01 amu’s x 6. 022 x 1023 /mol 6. 022 x 1023 amu/g = 44. 01 grams/mole Essentially: formula mass in grams = mass of 1 mole of substance Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 16

Mass and Moles of a Substance • The Mole Concept – A mole is defined as the number of atoms in exactly 12 grams of pure carbon– 12. (See Figure 3. 2) – The number of atoms in a 12 -gram sample of carbon – 12 is called Avogadro’s number (NA). – The value of Avogadro’s number is 6. 02 x 1023. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 17

Mass and Moles of a Substance • The molar mass of a substance is the mass of one mole of a substance. – is numerically equal to the formula weight in atomic mass units. – one mole of any element weighs its atomic mass in grams. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 18

Mass and Moles of a Substance • Mole calculations – Converting the number of moles of substance to its mass, and vice versa – This is known as the mass-mole relationship. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 19

Mass and Moles of a Substance • Mole calculations – Suppose we have 100. 0 grams of iron (Fe). The atomic weight of iron is 55. 8 g/mol. How many moles of iron does this represent? Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 20

Mass and Moles of a Substance • Mole calculations – Conversely, suppose we have 5. 75 moles of magnesium (atomic wt. = 24. 3 g/mol). What is its mass? Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 21

Mass and Moles of a Substance • Mole calculations – This same method applies to compounds. Suppose we have 100. 0 grams of H 2 O (molecular weight = 18. 0 g/mol). How many moles does this represent? Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 22

Mass and Moles of a Substance • Mole calculations – Conversely, suppose we have 3. 25 moles of glucose, C 6 H 12 O 6 (molecular wt. = 180. 0 g/mol). What is its mass? Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 23

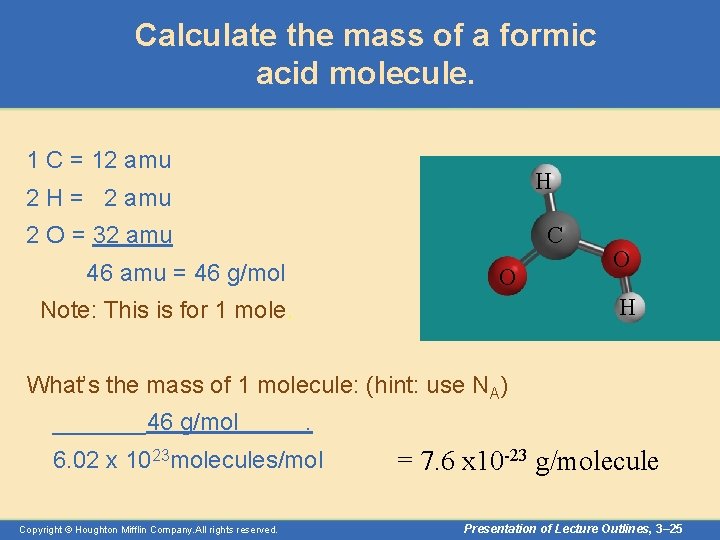
Examples of Calculations using Moles • What is the mass (in grams) of a molecule of formic acid? H C O O HCOOH Copyright © Houghton Mifflin Company. All rights reserved. H Presentation of Lecture Outlines, 3– 24

Calculate the mass of a formic acid molecule. 1 C = 12 amu H 2 H = 2 amu 2 O = 32 amu C 46 amu = 46 g/mol O O H Note: This is for 1 mole. What’s the mass of 1 molecule: (hint: use NA) _______46 g/mol . 6. 02 x 1023 molecules/mol Copyright © Houghton Mifflin Company. All rights reserved. = 7. 6 x 10 -23 g/molecule Presentation of Lecture Outlines, 3– 25

Mass and Moles and Number of Molecules or Atoms • The number of molecules or atoms in a sample is related to the moles of the substance: • Suppose we have a 3. 46 -g sample of hydrogen chloride, HCl. How many molecules of HCl does this represent? Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 26

Mole Calculations Example How many moles are there in 50 grams of sulfuric acid? Formula of sulfuric acid: H 2 SO 4 mol. wt. of H 2 SO 4 = 2 + 32 + 4(16) = 98 g/mol # mol = 50 g / (98 g/mol) = 0. 51 mol of H 2 SO 4 Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 27

Moles to Grams • How many grams are in 0. 025 mol of sodium hydroxide? Formula = Na. OH mol. wt. = 23 + 16 + 1 = 40 g/mol = (0. 025 mol)(40 g/mol) = 1 g of Na. OH Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 28

Determining Chemical Formulas • The percent composition of a compound is the mass percentage of each element in the compound. – We define the mass percentage of “A” as the parts of “A” per hundred parts of the total, by mass. That is, Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 29

Mass Percentages from Formulas • Let’s calculate the percent composition of butane, C 4 H 10. First, we need the molecular mass of C 4 H 10. Now, we can calculate the percents. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 30

Mass Percent using “grams” • Calculate the % of each element in Fe 2 O 3 by mass. Fe = 58. 5 grams/mol; O = 16. 0 grams/mol Formula weight = 2 (58. 5) + 3 (16) = 117 g/mol + 48 g/mol = 165 g/mol % Fe = 117 g/mol 165 g/mol (100%) = 71% %O = Copyright © Houghton Mifflin Company. All rights reserved. 48 g/mol 165 g/mol (100%) = 29% Presentation of Lecture Outlines, 3– 31

Using Mass Percent • How would one calculate the amount of an element is present in a given mass of sample? • In Fe 2 O 3, iron is 71% by mass in any sample. • How many grams of iron are present in a 258 g sample of iron (III) oxide? • Mass of Fe = (mass of sample) x (percent of Fe/100) • = (258 g) x (0. 71) • = 183 g of Fe Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 32

Determining Chemical Formulas • Determining the formula of a compound from the percent composition. – The percent composition of a compound leads directly to its empirical formula. – An empirical formula (or simplest formula) for a compound is the formula of the substance written with the smallest integer (whole number) subscripts. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 33

Determining Chemical Formulas • Determining the empirical formula from the percent composition. – Benzoic acid is a white, crystalline powder used as a food preservative. The compound contains 68. 8% C, 5. 0% H, and 26. 2% O by mass. What is its empirical formula? – In other words, give the smallest whole-number ratio of the subscripts in the formula C x H y. O z Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 34

Determining Chemical Formulas • Determining the empirical formula from the percent composition. – For the purposes of this calculation, we will assume we have 100. 0 grams of benzoic acid. – Then the mass of each element equals the numerical value of the percentage. – Since x, y, and z in our formula represent mole ratios, we must first convert these masses to moles. C x H y. O z Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 35

Determining Chemical Formulas • Determining the empirical formula from the percent composition. – Our 100. 0 grams of benzoic acid would contain: This isn’t quite a whole number ratio, but if we divide each number by the smallest of the three, a better ratio might emerge. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 36

Determining Chemical Formulas • Determining the empirical formula from the percent composition. – Our 100. 0 grams of benzoic acid would contain: now it’s not too difficult to See that the smallest whole number ratio is 7: 6: 2. The empirical formula is C 7 H 6 O 2. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 37

Determining Chemical Formulas • Determining the molecular formula from the empirical formula. – An empirical formula gives only the smallest whole -number ratio of atoms in a formula. – The molecular formula should be a multiple of the empirical formula (since both have the same percent composition). – To determine the molecular formula, we must know the molecular weight of the compound. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 38

Determining Chemical Formulas • Determining the molecular formula from the empirical formula. – For example, suppose the empirical formula of a compound is CH 2 O and its molecular weight is 60. 0 g/mol. – The molar weight of the empirical formula (the empirical weight) is only 30. 0 g/mol. – The ratio of the formula mass to empirical mass determines the whole number multiple. molecular C 2 H 4 O 2 whole # = =n empirical Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 39

Stoichiometry: Quantitative Relations in Chemical Reactions • Stoichiometry is the calculation of the quantities of reactants and products involved in a chemical reaction. – It is based on the balanced chemical equation and on the relationship between mass and moles. – Stoichiometric calculations involve mole-to-mole and mass-mole relationships from balanced equations. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 40

Molar Interpretation of a Chemical Equation • The balanced chemical equation represents molecule-to-molecule, or “mole-to-mole” relationships. – For example, the Haber process for producing ammonia involves the reaction of hydrogen and nitrogen. reactants Copyright © Houghton Mifflin Company. All rights reserved. products Presentation of Lecture Outlines, 3– 41

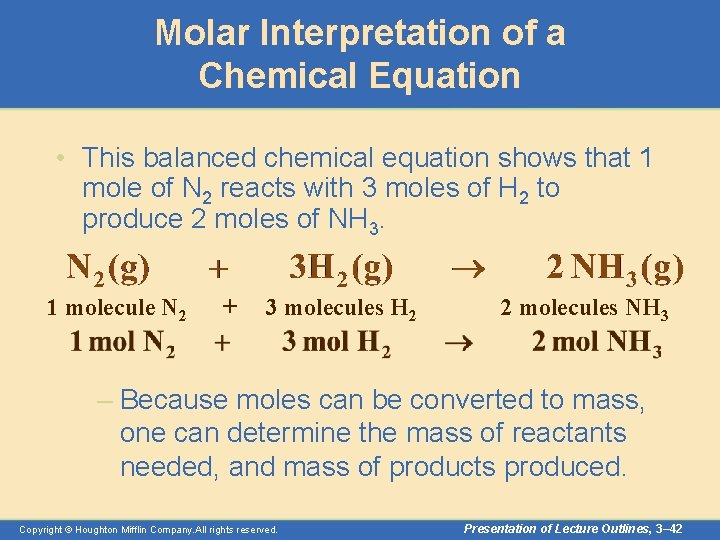
Molar Interpretation of a Chemical Equation • This balanced chemical equation shows that 1 mole of N 2 reacts with 3 moles of H 2 to produce 2 moles of NH 3. 1 molecule N 2 + 3 molecules H 2 2 molecules NH 3 – Because moles can be converted to mass, one can determine the mass of reactants needed, and mass of products produced. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 42

Molar Interpretation of a Chemical Equation • Suppose we wished to determine the number of moles of NH 3 we could obtain from 4. 8 mol H 2. – Because the coefficients in the balanced equation represent mole-to-mole ratios, the calculation is simple. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 43

Mass Relationships in Chemical Equations • Amounts of substances in a chemical reaction by mass. – How many grams of HCl are required to react with 5. 00 grams manganese (IV) oxide according to this equation? Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 44

Mass Relationships in Chemical Equations • First, you write what is given (5. 00 g Mn. O 2) and convert this to moles. • Then convert to moles of what is desired. (mol HCl) • Finally, you convert this to mass (g HCl) Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 45

Example 2 Solid lithium hydroxide is used by space vehicles to remove exhaled carbon dioxide from the living environment. The products of the reaction are solid lithium carbonate and liquid water. What mass of gaseous carbon dioxide can 1 kg of lithium hydroxide absorb? Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 46

Example 2 Write down the equation for the reaction and balance it: 2 Li. OH + CO 2 Li 2 CO 3 + H 2 O Next, convert the initial mass of Li. OH to moles 1 kg 1 mol 24 g/mol = 41. 8 mol of Li. OH Use the mole ratio of CO 2 to Li. OH to calculate the moles of CO 2 needed. 41. 8 mol 1 mol CO 2 2 mol Li. OH Copyright © Houghton Mifflin Company. All rights reserved. = 20. 9 mol CO 2 Presentation of Lecture Outlines, 3– 47

Example 2 Finally, Convert moles of CO 2 to grams of CO 2 44 g CO 2 20. 9 mol CO 2 1 mol CO 2 = 920 g of CO 2 Thus, 1 kg of Li. OH can absorb 920 g of CO 2 Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 48

Limiting Reagent • The limiting reactant (or limiting reagent) is the reactant that is entirely consumed when the reaction goes to completion. (See Figure 3. 14) – The limiting reagent determines how much product can be produced. – For example, bicycles require one frame and two wheels. – If you have 20 wheels but only 5 frames, how many bicycles can be made? – How many wheels are left? Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 49

Limiting Reagent • Zinc metal reacts with hydrochloric acid by the following reaction. – If 0. 30 mol Zn is added to hydrochloric acid containing 0. 52 mol HCl, how many moles of H 2 are produced? Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 50

Limiting Reagent • From each reactant one can calculate the amount of product to expect. • The reactant that gives the smaller amount is the limiting reagent. • Since HCl is the limiting reagent, theoretical yield of H 2 is 0. 26 mol. (How many grams of HCl? ) Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 51

Theoretical and Percent Yield • The theoretical yield refers to the maximum amount of product can be produced from a given amounts of reactants. – The percentage yield is the actual yield (experimental amount) divided by theoretical yield (ie. , the calculated yield) x 100%. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 52

Theoretical and Percent Yield • In the previous example theoretical yield of H 2 was 0. 26 mol (or 0. 52 g) H 2. • An experiment was performed, and the amount of H 2 obtained was only 0. 22 g H 2. • Calculate the %Yield of H 2 = (A. Y. /T. Y. ) x 100% Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 53

Operational Skills • • • Calculating the formula weight from a formula. Calculating the mass of an atom or molecule. Converting moles of substance to grams and vice versa. Calculating the number of molecules in a given mass. Calculating the percentage composition from the formula. Calculating the mass of an element in a given mass of compound. Calculating the percentages C and H by combustion. Determining the empirical formula from percentage composition. Determining the true molecular formula. Relating quantities in a chemical equation. Calculations with a limiting reagent, actual yield, theoretical yield and percent yield. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 54

End of Chapter 3 Practice Problems 6, 8, 10, 12 (balance them), 14, 18, 20, 27, 28, 30, 34, 40, 46 (balance them), 51, 52, 56, 62, 63, 83, 97. Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 55

Figure 3. 2: One mole each of various substances. Photo courtesy of American Color. Return to Slide 5 Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 56

Figure 3. 14: Limiting reactant analogy using cheese sandwiches. Return to Slide 28 Copyright © Houghton Mifflin Company. All rights reserved. Presentation of Lecture Outlines, 3– 57