Calculation of Reduction Potential of FAD in MCAD

Calculation of Reduction Potential of FAD in MCAD using Combined DFTB/MM Simulations Sudeep Bhattacharyay, Marian Stankovich, and Jiali Gao

Overview n Objective n Methods of calculation and strategies n Results n Future Directions

Flavoenzymes q Mediates electron transfer q Flavin ring shuttles between reduced and oxidized states q Protein environment controls the reduction potential of FAD q Coupled electron-proton transfer q p. Ka from experiment often misleading if that is observed through a observable signature belonging to a particular redox state q Need to predict correctly through simulation q Requires accuracy in a) reduction potential calculation and b) p. Ka calculation

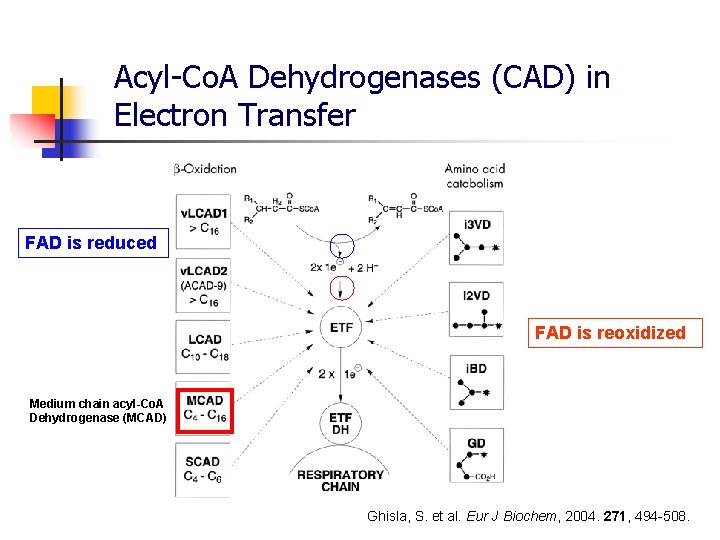
Acyl-Co. A Dehydrogenases (CAD) in Electron Transfer FAD is reduced FAD is reoxidized Medium chain acyl-Co. A Dehydrogenase (MCAD) Ghisla, S. et al. Eur J Biochem, 2004. 271, 494 -508.

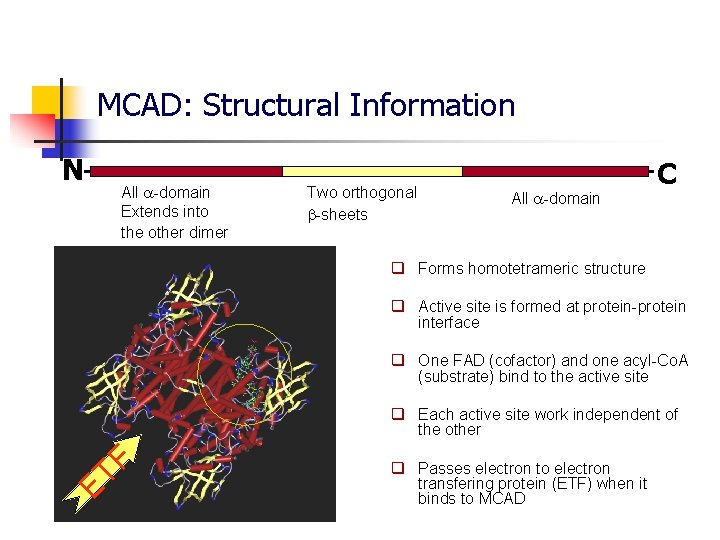
MCAD: Structural Information N All -domain Extends into the other dimer Two orthogonal -sheets All -domain C q Forms homotetrameric structure q Active site is formed at protein-protein interface q One FAD (cofactor) and one acyl-Co. A (substrate) bind to the active site ET F q Each active site work independent of the other q Passes electron to electron transfering protein (ETF) when it binds to MCAD

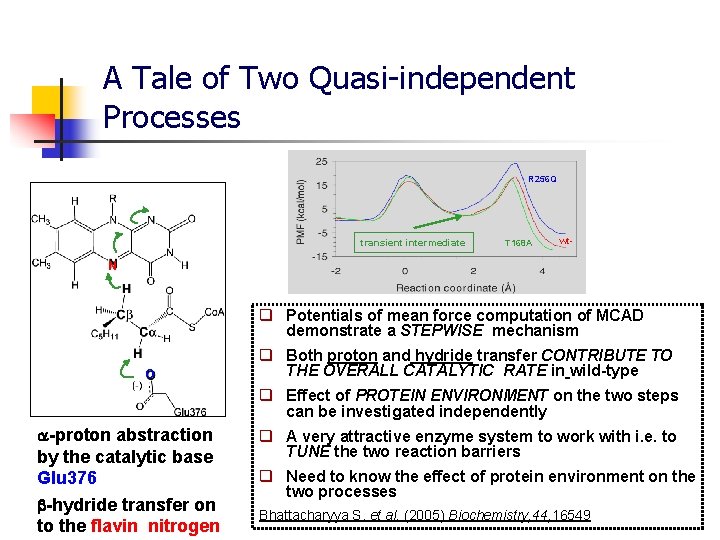
A Tale of Two Quasi-independent Processes R 256 Q transient intermediate T 168 A wt- N q Potentials of mean force computation of MCAD demonstrate a STEPWISE mechanism O q Both proton and hydride transfer CONTRIBUTE TO THE OVERALL CATALYTIC RATE in wild-type q Effect of PROTEIN ENVIRONMENT on the two steps can be investigated independently -proton abstraction by the catalytic base Glu 376 -hydride transfer on to the flavin nitrogen q A very attractive enzyme system to work with i. e. to TUNE the two reaction barriers q Need to know the effect of protein environment on the two processes Bhattacharyya S. et al. (2005) Biochemistry, 44, 16549

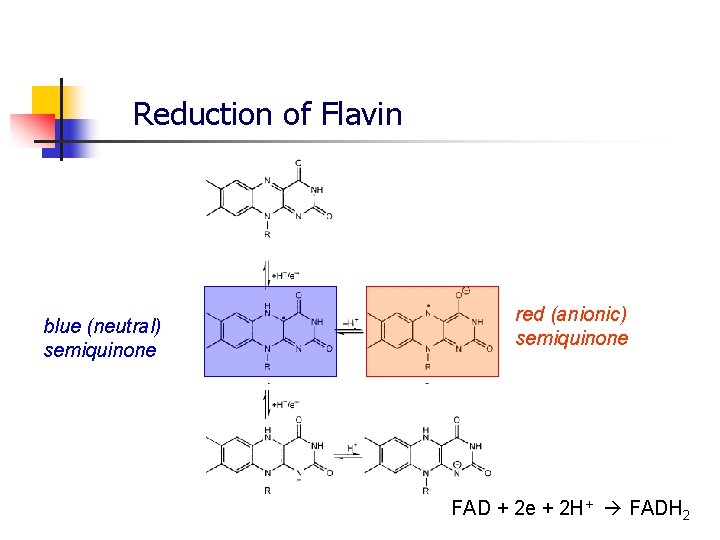
Reduction of Flavin blue (neutral) semiquinone red (anionic) semiquinone FAD + 2 e + 2 H+ FADH 2

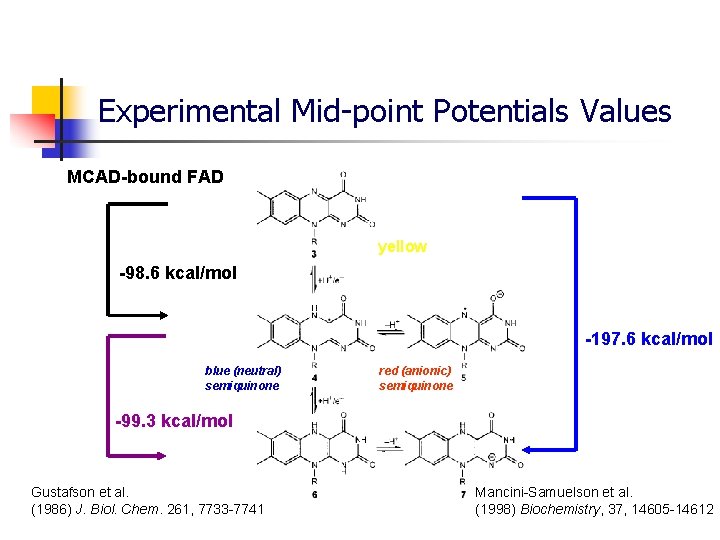
Experimental Mid-point Potentials Values MCAD-bound FAD yellow -98. 6 kcal/mol -197. 6 kcal/mol blue (neutral) semiquinone red (anionic) semiquinone -99. 3 kcal/mol Gustafson et al. (1986) J. Biol. Chem. 261, 7733 -7741 Mancini-Samuelson et al. (1998) Biochemistry, 37, 14605 -14612

Methods and Strategies q Hybrid QM/MM methods; calculation of electron and proton affinities q Thermodynamic integration through FEP q Dual topology single coordinate method q Boundary condition

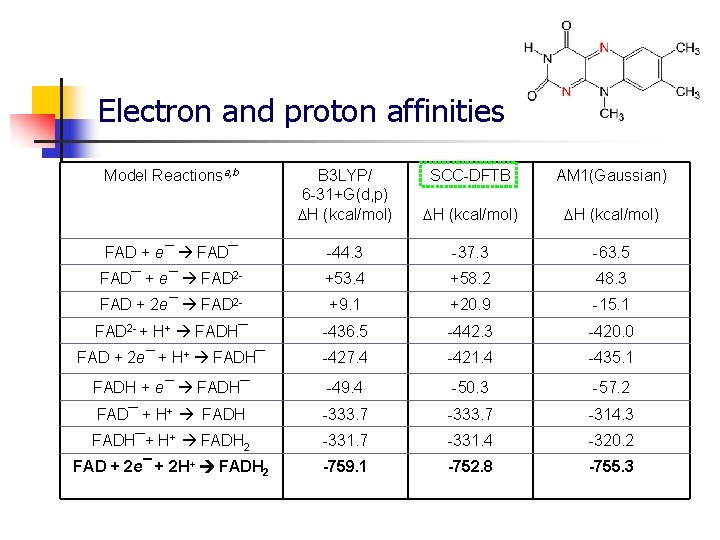
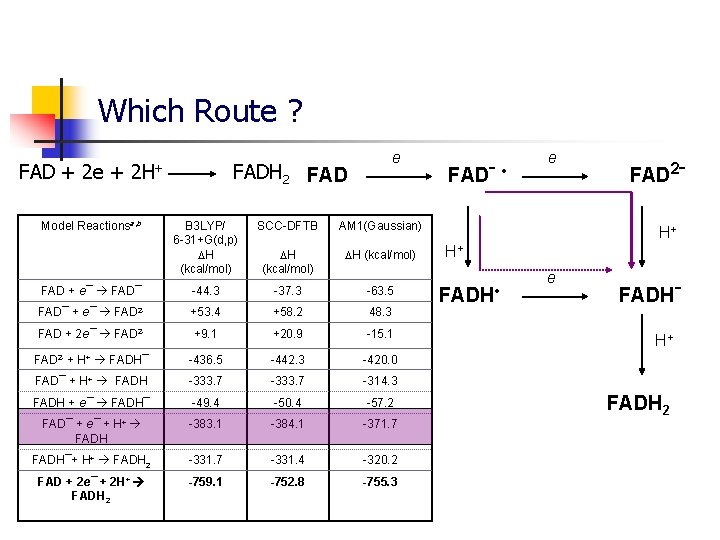
Electron and proton affinities Model Reactionsa, b B 3 LYP/ 6 -31+G(d, p) H (kcal/mol) SCC-DFTB AM 1(Gaussian) H (kcal/mol) FAD + e¯ FAD¯ -44. 3 -37. 3 -63. 5 FAD¯ + e¯ FAD 2 - +53. 4 +58. 2 48. 3 FAD + 2 e¯ FAD 2 - +9. 1 +20. 9 -15. 1 FAD 2 - + H+ FADH¯ -436. 5 -442. 3 -420. 0 FAD + 2 e¯ + H+ FADH¯ -427. 4 -421. 4 -435. 1 FADH + e¯ FADH¯ -49. 4 -50. 3 -57. 2 FAD¯ + H+ FADH -333. 7 -314. 3 FADH¯+ H+ FADH 2 -331. 7 -331. 4 -320. 2 FAD + 2 e¯ + 2 H+ FADH 2 -759. 1 -752. 8 -755. 3

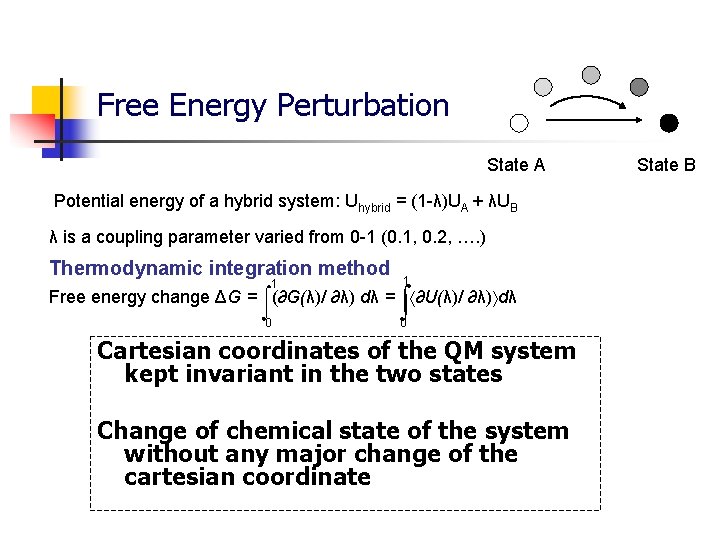
Free Energy Perturbation State A Potential energy of a hybrid system: Uhybrid = (1 -λ)UA + λUB λ is a coupling parameter varied from 0 -1 (0. 1, 0. 2, …. ) Thermodynamic integration method 1 ∫ Free energy change ΔG = (∂G(λ)/ ∂λ) dλ = ∂U(λ)/ ∂λ) dλ 0 0 Cartesian coordinates of the QM system kept invariant in the two states Change of chemical state of the system without any major change of the cartesian coordinate State B

QM/MM Interactions With same number of atoms in the two chemical states Utot (R) = │ĤQM+Ĥel. QM/MM │ + Uvan. QM/MM (R) + Ubonded. QM/MM (R) + UMM (R) electronic energy of the QM system + the electrostatic interaction energy van der Waals bonded energy of the MM atoms Li, G. et al. J. Phys. Chem. B (2003) 107, 8643 G (R; λ) = λ UA/MM(RQM , RMM ) + UB/MM(RQM , RMM ) Only the electrostatic term contributes to the free energy derivative as the two states have same cartesian coordinate

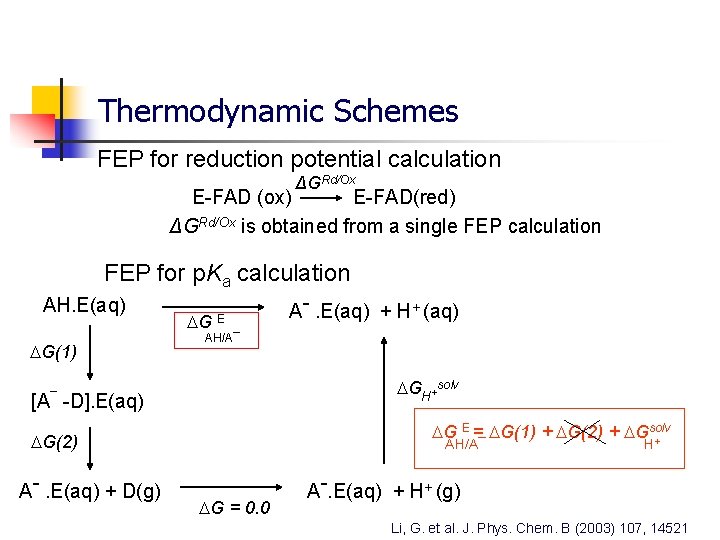
Thermodynamic Schemes FEP for reduction potential calculation ΔGRd/Ox E-FAD (ox) E-FAD(red) ΔGRd/Ox is obtained from a single FEP calculation FEP for p. Ka calculation AH. E(aq) G(1) [A¯ G E AH/A¯ GH+solv -D]. E(aq) G E = G(1) + G(2) + Gsolv + G(2) Aˉ. E(aq) + D(g) Aˉ. E(aq) + H+ (aq) AH/A¯ G = 0. 0 H Aˉ. E(aq) + H+ (g) Li, G. et al. J. Phys. Chem. B (2003) 107, 14521

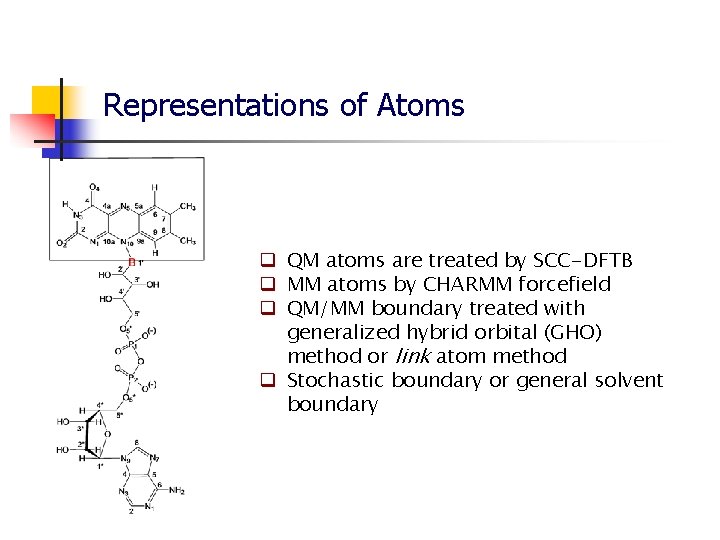
Representations of Atoms q QM atoms are treated by SCC-DFTB q MM atoms by CHARMM forcefield q QM/MM boundary treated with generalized hybrid orbital (GHO) method or link atom method q Stochastic boundary or general solvent boundary

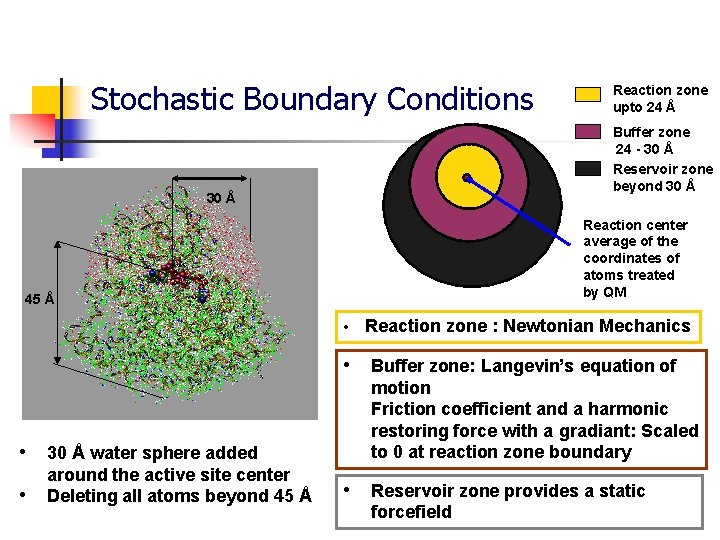
Stochastic Boundary Conditions Reaction zone upto 24 Å Buffer zone 24 - 30 Å Reservoir zone beyond 30 Å Reaction center average of the coordinates of atoms treated by QM 45 Å • Reaction zone : Newtonian Mechanics • Buffer zone: Langevin’s equation of • 30 Å water sphere added • around the active site center Deleting all atoms beyond 45 Å motion Friction coefficient and a harmonic restoring force with a gradiant: Scaled to 0 at reaction zone boundary • Reservoir zone provides a static forcefield

Which Route ? FAD + 2 e + 2 H+ Model Reactionsa, b FADH 2 FAD e B 3 LYP/ 6 -31+G(d, p) H (kcal/mol) SCC-DFTB AM 1(Gaussian) H (kcal/mol) -44. 3 -37. 3 -63. 5 FAD 2 - +53. 4 +58. 2 48. 3 FAD + 2 e¯ FAD 2 - +9. 1 +20. 9 -15. 1 FAD 2 - + H+ FADH¯ -436. 5 -442. 3 -420. 0 FAD¯ + H+ FADH -333. 7 -314. 3 FADH + e¯ FADH¯ -49. 4 -50. 4 -57. 2 FAD¯ + e¯ + H+ FADH -383. 1 -384. 1 -371. 7 FADH¯+ H+ FADH 2 -331. 7 -331. 4 -320. 2 FAD + 2 e¯ + 2 H+ FADH 2 -759. 1 -752. 8 -755. 3 FAD + e¯ FAD¯ + e¯ FADˉ • e FAD 2ˉ H+ H+ FADH • e FADHˉ H+ FADH 2

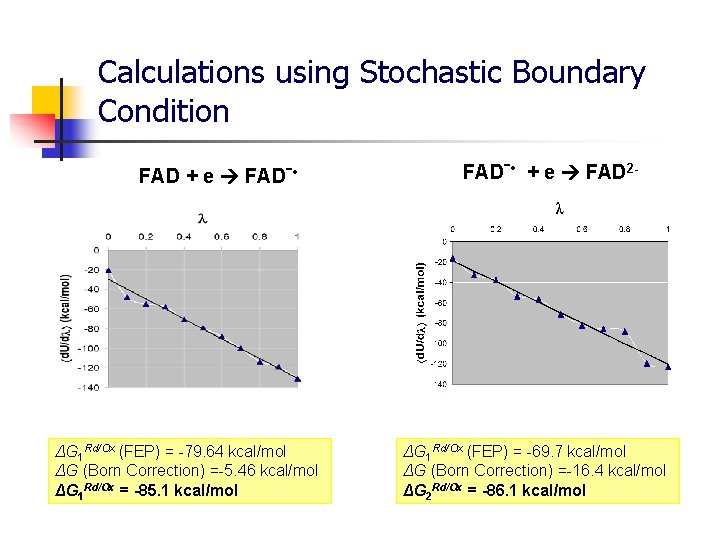
Calculations using Stochastic Boundary Condition FAD + e FADˉ • ΔG 1 Rd/Ox (FEP) = -79. 64 kcal/mol ΔG (Born Correction) =-5. 46 kcal/mol ΔG 1 Rd/Ox = -85. 1 kcal/mol FADˉ • + e FAD 2 - ΔG 1 Rd/Ox (FEP) = -69. 7 kcal/mol ΔG (Born Correction) =-16. 4 kcal/mol ΔG 2 Rd/Ox = -86. 1 kcal/mol

Calculated Reduction Potential Enzyme mid-point reduction potential for MCAD-bound FAD + 2 e + 2 H+ FADH 2 Em = -145 m. V G = -197. 9 kcal/mol (E-FAD 2 - /E-FADH-) ΔGtotal = ΔG 1 Rd/Ox + ΔG 2 Rd/Ox + G -85 -86 -56 + (E-FADH- /E-FADH 2) G -30 Estimated ΔGtotal = -256 kcal/mol; Overestimated energy ~ 60 kcal/mol Possible reason for this overestimation Ø Long-range electrostatic interactions

Test Calculations Ø Stochastic boundary set up with net charge of the complex set to zero Ø General solvent boundary condition Ø Matching with experimental results

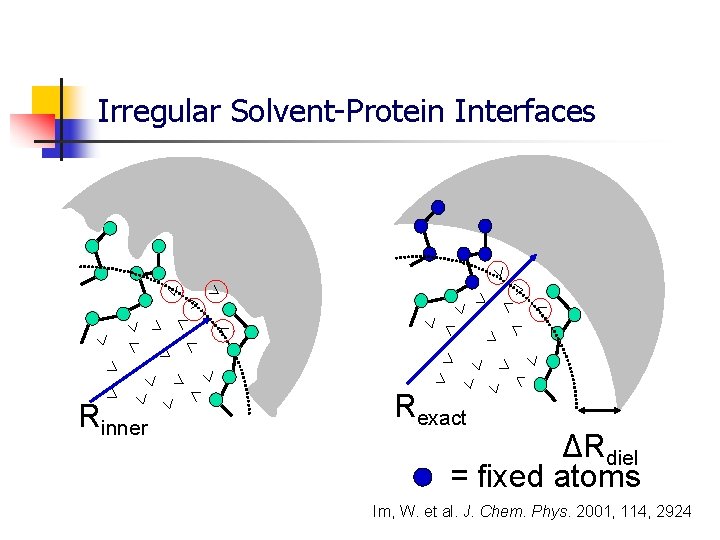
Treating Solvation with General Solvent Boundary Potential (GSBP) q Inner region atoms (ligand + part of enzyme + solvent) treated explicitly q Outer region: Atoms of enzyme are treated explicitly but the solvent is represented as a continuous dielectric medium Im, W. et al. J. Chem. Phys. 2001, 114, 2924

Setup of Zones in GSBP Inner zone upto 16 Å Buffer zone upto 18 Å Secondary buffer (18 -20) Å Reaction center Protein atoms which have 1 -3 connections with reservoir zone are kept fixed Reservoir zone > 20 Å q Inner region atoms (ligand + part of enzyme + solvent) treated explicitly (< 16 Å) q Water atoms deleted beyond 18 Å q Charges of residues beyond 20 Å set to 0 q Protein atom fixed beyond 20 Å q Outer region: Atoms of enzyme are treated explicitly but the solvent is represented as a continuous dielectric medium

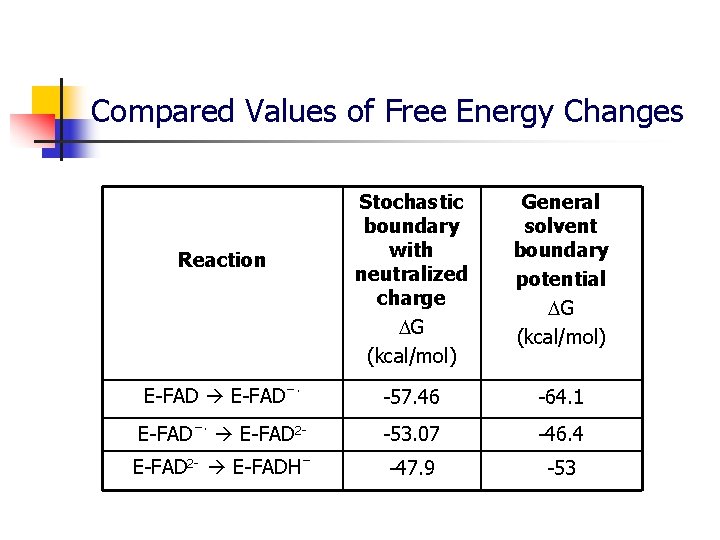
Compared Values of Free Energy Changes Stochastic boundary with neutralized charge G (kcal/mol) General solvent boundary potential G (kcal/mol) E-FADˉ· -57. 46 -64. 1 E-FADˉ· E-FAD 2 - -53. 07 -46. 4 E-FAD 2 - E-FADHˉ -47. 9 -53 Reaction

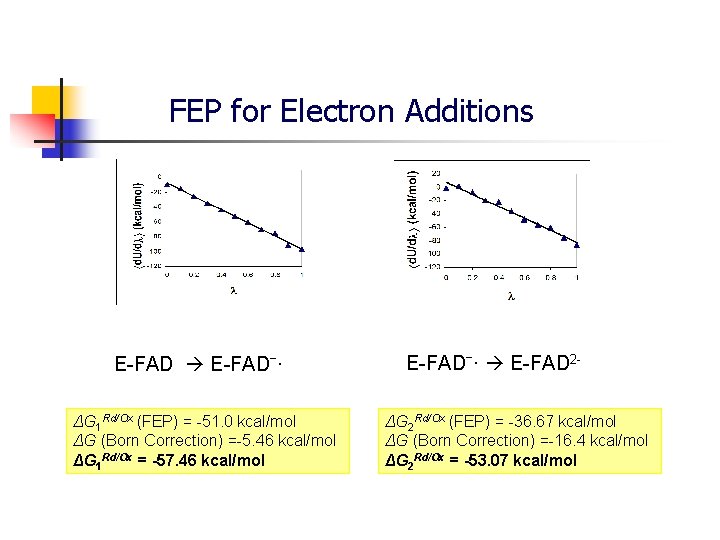
FEP for Electron Additions E-FADˉ· ΔG 1 Rd/Ox (FEP) = -51. 0 kcal/mol ΔG (Born Correction) =-5. 46 kcal/mol ΔG 1 Rd/Ox = -57. 46 kcal/mol E-FADˉ· E-FAD 2ΔG 2 Rd/Ox (FEP) = -36. 67 kcal/mol ΔG (Born Correction) =-16. 4 kcal/mol ΔG 2 Rd/Ox = -53. 07 kcal/mol

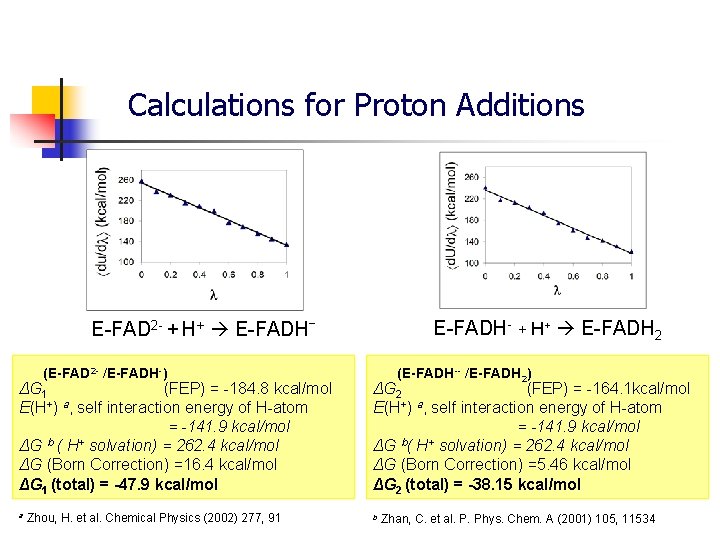
Calculations for Proton Additions E-FADH- + H+ E-FADH 2 E-FAD 2 - + H+ E-FADHˉ (E-FAD 2 - /E-FADH-) ΔG 1 (FEP) = -184. 8 kcal/mol E(H+) a, self interaction energy of H-atom = -141. 9 kcal/mol b + ΔG ( H solvation) = 262. 4 kcal/mol ΔG (Born Correction) =16. 4 kcal/mol ΔG 1 (total) = -47. 9 kcal/mol a Zhou, H. et al. Chemical Physics (2002) 277, 91 (E-FADH-- /E-FADH 2) ΔG 2 (FEP) = -164. 1 kcal/mol E(H+) a, self interaction energy of H-atom = -141. 9 kcal/mol b + ΔG ( H solvation) = 262. 4 kcal/mol ΔG (Born Correction) =5. 46 kcal/mol ΔG 2 (total) = -38. 15 kcal/mol b Zhan, C. et al. P. Phys. Chem. A (2001) 105, 11534

FEP Electron Addition FAD e √ FADˉ • e √ H+ FADH • FAD 2ˉ H+ e ? √ √ FADHˉ H+ FADH 2 √ E-FADH· E-FADHˉ ΔG 1 Rd/Ox (FEP) = -55. 47 kcal/mol ΔG (Born Correction) =-5. 46 kcal/mol ΔG 1 Rd/Ox = -60. 93 kcal/mol

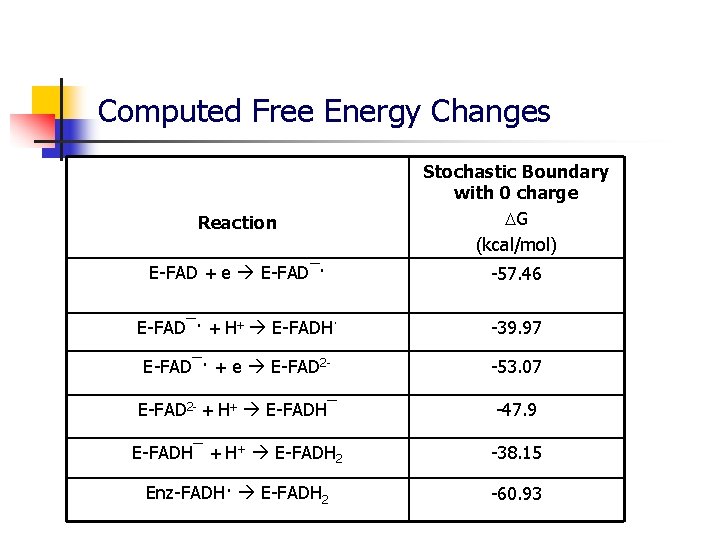
Computed Free Energy Changes Reaction Stochastic Boundary with 0 charge G (kcal/mol) E-FAD + e E-FAD¯· -57. 46 E-FAD¯· + H+ E-FADH· -39. 97 E-FAD¯· + e E-FAD 2 - -53. 07 E-FAD 2 - + H+ E-FADH¯ -47. 9 E-FADH¯ + H+ E-FADH 2 -38. 15 Enz-FADH· E-FADH 2 -60. 93

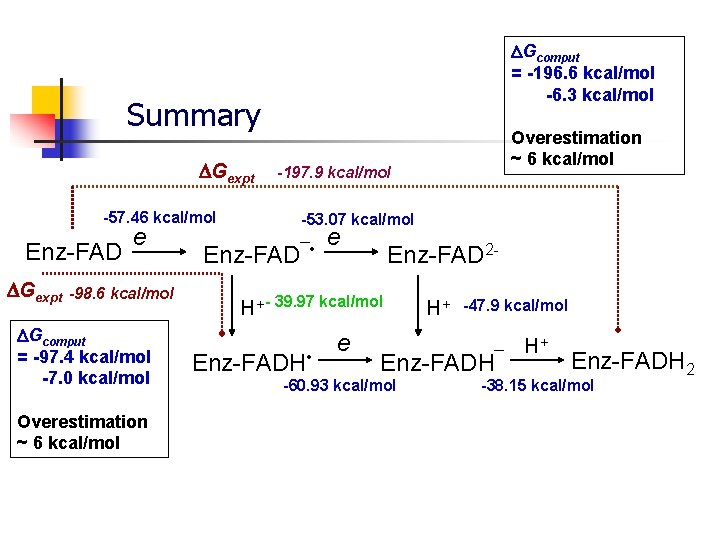
Gcomput = -196. 6 kcal/mol -6. 3 kcal/mol Summary Gexpt -57. 46 kcal/mol Enz-FAD Gexpt e -98. 6 kcal/mol Gcomput = -97. 4 kcal/mol -7. 0 kcal/mol Overestimation ~ 6 kcal/mol -197. 9 kcal/mol -53. 07 kcal/mol Enz-FAD¯ • e Enz-FAD 2 - H+ - 39. 97 kcal/mol Enz-FADH • e H+ -47. 9 kcal/mol Enz-FADH¯ -60. 93 kcal/mol H+ Enz-FADH 2 -38. 15 kcal/mol

Conclusions q q q q The two-electron two-proton reduction potential of FAD in MCAD was calculated Both reduction potential calculations yield results that are consistent to the experimental values Computed 2 e/2 H+ reduction potential for FAD bound MCAD is -180 m. V, which is 35 m. V more negative than the experimental value The first reduction potential of MCAD-bound FAD was calculated to be ~ -103 kcal/mol compared to the experimentally observed value of -98. 6 kcal/mol Computed second reduction potential for MCAD-bound FAD was ~ -105 kcal/mol, about 6 kcal/mol more negative than the experimentally observed value of -99. 3 kcal/mol This calculation shows that at neutral p. H MCAD-bound FAD will be converted to the hydroquinone form FADH 2 through a two electrons/two protons reduction p. Ka calculation of E-FADH¯ and E-FADH 2 show that both values are quite high: 35 and 27, respectively. The p. Ka of E-FADH • was calculated to be ~30 Future Directions Ø Ø Using the method to compute the reduction potential and p. Ka of FAD and FMN in aqueous solution pka calculation of acyl-Co. A substrate bound to MCAD

Acknowledgements $ NIH Professor Jiali Gao Professor Don G. Truhlar Dr. Kowangho Nam Dr. Alessandro Cembran Dr. Marian Stankovich Dr. Qiang Cui Dr. Haibo Yu Minnesota Supercomputing Institute

Converting FAD Reduction Potential FAD + 2 e + 2 H+ FADH 2 (FAD 2 - /FADH 2) Total = S 1 + S 2 + GS Em = -( Total)/n. F + NHE ; n = number of electrons = 2 F= Faraday constant = 23. 06 kcal/mol Total - n. F NHE = -n. FEm , F = 23. 06 kcal/(mol. V) For FAD bound MCAD: n. F NHE = -n 4. 43 F V = -2 x 4. 43 x 23. 06 kcal/mol = -204. 31 kcal/mol Mid point potential, E 0 = -0. 145 V For FAD-MCAD: E 0 = -0. 145 V Lenn, N. D. Stankovich, M. T. Liu, H. Biochemistry, 1990, 29, 3709 Thus Total - n. F NHE = -n. F x (-0. 145) = -2 x 23. 06 x (-0. 145) kcal/mol = 6. 687 kcal/mol Thus Total = (6. 687 + n. F NHE ) kcal/mol = (6. 687 -204. 31) kcal/mol = -197. 6 kcal/mol

Calculating Absolute Reduction Potential Standard Hydrogen Electrode (Normal Hydrogen Electrode) = Free energy change, EH 0 in the reaction H+ (s) + e¯ ½H 2 (g) EH 0 For a general reduction process: M (s) + e¯ M¯(s) EM M¯ Then combining the above 2 equations ½H 2 (g) + M(s) M¯(s) + H+ (s) => EM M¯ = (E 0 + EH 0) E 0 H = -4. 43 e. V

Irregular Solvent-Protein Interfaces Rinner Rexact ΔRdiel = fixed atoms Im, W. et al. J. Chem. Phys. 2001, 114, 2924