Calculating Validity Truth tables can be used to

Calculating Validity Truth tables can be used to calculate validity.

Calculating Validity Truth tables can be used to calculate validity. The Fundamental Question: Is this possible: the premises are T and the conclusion F?

Calculating Validity Truth tables can be used to calculate validity. The Fundamental Question: Is this possible: the premises are T and the conclusion F? If this is possible, then the argument is invalid. Otherwise it is valid.

Calculating Validity Truth tables can be used to calculate validity. The Fundamental Question: Is this possible: the premises are T and the conclusion F? If this is possible, then the argument is invalid. Otherwise it is valid. Valid Defined: 1. Assuming the premises are (all) T, the conclusion has to be T. 2. It is impossible for the premises to be T, and the conclusion to be F.

Invalid Example Is the argument R>W, W | R valid? R T F W T T F F R>W W | R

Invalid Example Is the argument R>W, W | R valid? R T F W T T F F R>W W | R T T F F T F F

Invalid Example Is the argument R>W, W | R valid? R T F W T T F F R>W W | R T TT T T F T FF F TF F F

Invalid Example Is the argument R>W, W | R valid? R T F W T T F F R>W W | R T TT T T F T FF F TF F F Is there a row where the premises are T and the conclusion is F?

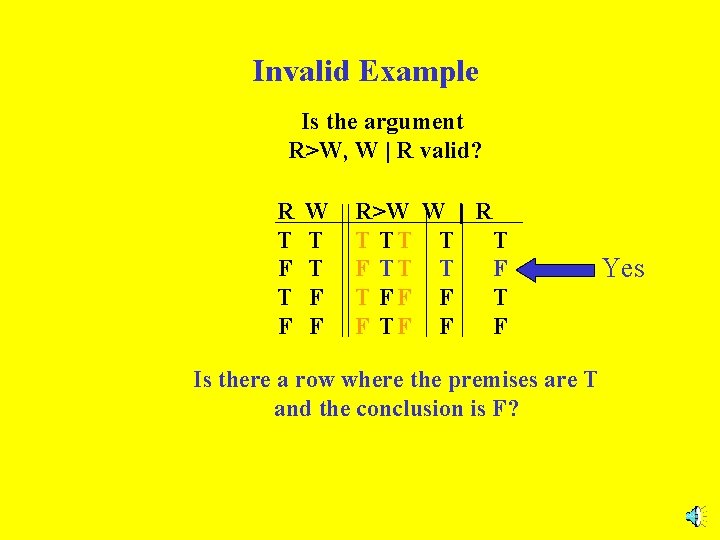
Invalid Example Is the argument R>W, W | R valid? R T F W T T F F R>W W | R T TT T T F T FF F TF F F Is there a row where the premises are T and the conclusion is F? Yes

Invalid Example Is the argument R>W, W | R valid? R T F W T T F F R>W W | R T TT T T F T FF F TF F F Is there a row where the premises are T and the conclusion is F? THE ARGUMENT IS INVALID. Yes

Counterexample A counterexample is a row of a table where the premises are T and the conclusion is false. R T F W T T F F R>W W | R T TT T T F T FF F TF F F Counterexample

Counterexample A counterexample is a row of a table where the premises are T and the conclusion is false. R T F W T T F F R>W W | R T TT T T F T FF F TF F F Counterexample Third Definition of Validity An argument is valid iff it has no counterexample.

Valid Example Is the argument A>G, A | G valid? A T F G T T F F A>G A | G T TT T T FF T F F TF F F Is there a row where the premises are T and the conclusion is F?

Valid Example Is the argument A>G, A | G valid? A T F G T T F F A>G A | G T TT T T FF T F F TF F F Counterexample? Is there a row where the premises are T and the conclusion is F?

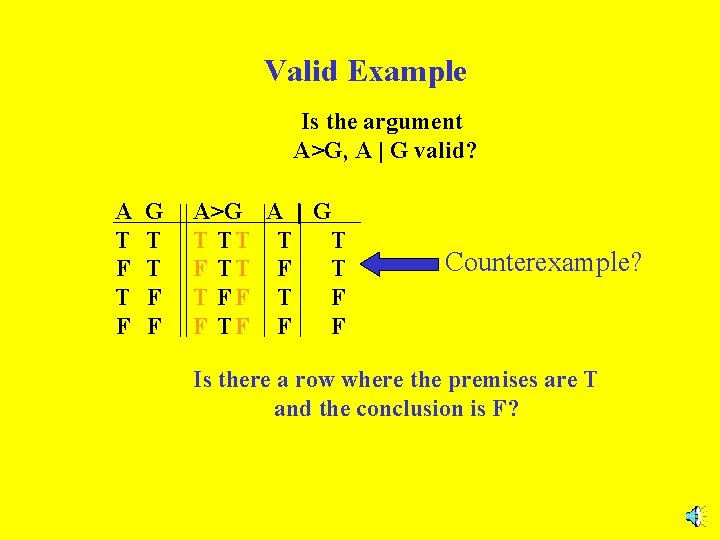
Valid Example Is the argument A>G, A | G valid? A T F G T T F F A>G A | G T TT T T FF T F F TF F F Counterexample? Is there a row where the premises are T and the conclusion is F?

Valid Example Is the argument A>G, A | G valid? A T F G T T F F A>G A | G T TT T T FF T F F TF F F Counterexample? Is there a row where the premises are T and the conclusion is F?

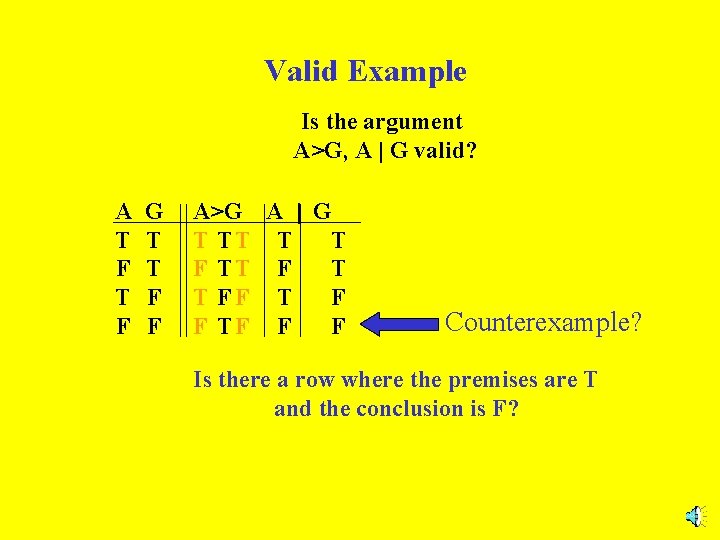
Valid Example Is the argument A>G, A | G valid? A T F G T T F F A>G A | G T TT T T FF T F F TF F F Counterexample? Is there a row where the premises are T and the conclusion is F?

Valid Example Is the argument A>G, A | G valid? A T F G T T F F A>G A | G T TT T T No Counterexample! F TT F T The argument is T FF T F VALID. F TF F F Is there a row where the premises are T and the conclusion is F? For more click here