Calculating the shape of a polynomial from regression

Calculating the shape of a polynomial from regression coefficients Jane E. Miller, Ph. D The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Overview • Functional form of a polynomial • Solving a polynomial for values of the independent variable • Illustrative example – Calculations – Chart • Spreadsheet to perform calculations The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Specifying a model with a polynomial • To specify a polynomial function of an independent variable (IV), include linear and higher-order terms for that IV in the model. E. g. , – A quadratic specification will include linear and square terms (variables): Y = β 0 + β 1 X 1 + β 2 X 1 2 – A cubic specification will include linear, square, and cubic terms: y = β 0 + β 1 X 1 + β 2 X 1 2 + β 3 X 1 3 The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Example: Birth weight as a quadratic function of IPR • If a birth weight model includes both incometo-poverty ratio (IPR) and IPR 2 as independent variables, it yields the following quadratic specification: Birth weight = β 0 + (βIPR × IPR) + (βIPR 2 × IPR 2) – βIPR is the coefficient on the linear term – βIPR 2 is the coefficient on the square term – IPR is the value of the income-to-poverty ratio variable for each case – IPR 2 is IPR-squared for each case The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Solving a polynomial based on βs • Birth weight (grams) = β 0 + (βIPR × IPR) + (βIPR 2 × IPR 2) • Substituting the estimated βs into the general equation gives: Birth weight (grams) = 3, 317. 8 + (80. 5 IPR) + (– 9. 9 IPR 2) • Which can be solved for specific values of IPR • Estimated coefficients are shown in table 9. 1 of The Chicago Guide to Writing about Multivariate Analysis, 2 nd Edition. The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Calculating the shape of the polynomial, holding constant all other IVs • To calculate the effect of the IV in the polynomial holding constant all other independent variables in the model – The intercept (β 0) and the βis related to other IVs in the model will cancel out when you subtract to calculate the difference between values. – So you don’t have to include those coefficients in these calculations. The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

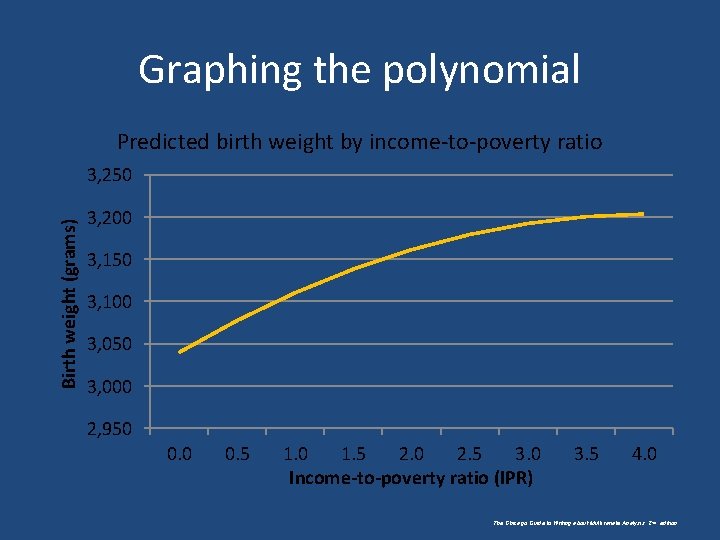
Calculating predicted values of the dependent variable (DV) for different values of the IV • Solve the equation (80. 5 IPR) + (– 9. 9 IPR 2) for each of several selected values of X 1. E. g. , – At IPR = 1. 0 • Birth weight = (80. 5 1. 0) + (– 9. 9 1. 02) = 70. 6 grams – At IPR = 2. 0 • Birth weight = (80. 5 2. 0) + (– 9. 9 2. 02) = 121. 4 grams – At IPR = 3. 0 • Birth weight = (80. 5 3. 0) + (– 9. 9 3. 02) = 151. 8 grams βIPR = 80. 5; βIPR 2 = – 9. 9. We ignore β 0 because it cancels out when we subtract to calculate differences across predicted values, in the next step. The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Selecting values of the IV for which to calculate the predicted DV • Select values of the IV to solve for by picking 5 or 6 values that span the observed range of Xi in your data. E. g. , – The income-to-poverty ratio (IPR) ranges from 0 to 5, so plug in values at 1 -unit increments across that range. – Mother’s age ranges from 15 to 49, so if your model specifies a polynomial function of age, solve it for values at 5 -year increments across that range. • Avoid selecting out of range values, since they were not included in the model that estimated the βs. The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Calculating the effect of changes in the IV on the DV • Compute the difference in predicted value of the dependent variable (DV, Y) by subtracting predicted values of Y for different values of the IV (Xi). – E. g. , predicted Y (Xi = 2) – predicted Y (Xi = 1) • Important to do this for several pairs of values of the IV because when the association is specified with a polynomial, by definition, Xi will not have a constant marginal effect on Y. The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Example: Birth weight as a quadratic function of IPR • As we saw earlier: – At IPR = 1. 0, predicted birth weight = 70. 6 grams – At IPR = 2. 0, predicted birth weight = 121. 4 grams – At IPR = 3. 0, predicted birth weight = 151. 8 grams • Thus the marginal effect of moving from IPR = 1. 0 to IPR = 2. 0 is 121. 4 – 70. 6 = 50. 8 grams IPR = 2. 0 to IPR = 3. 0 is 151. 8 – 131. 4 = 30. 4 grams The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Graphing the polynomial Predicted birth weight by income-to-poverty ratio Birth weight (grams) 3, 250 3, 200 3, 150 3, 100 3, 050 3, 000 2, 950 0. 5 1. 0 1. 5 2. 0 2. 5 3. 0 Income-to-poverty ratio (IPR) 3. 5 4. 0 The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Coefficients and shape of the quadratic • In this example, the decreasing marginal positive effect of IPR on birth weight is due to the combination of – a positive βIPR – a negative βIPR 2 • Recall: βIPR = 80. 5; βIPR 2 = – 9. 9 • Other combinations of positive and negative signs on the linear and squared terms will generate different shapes of the quadratic function. The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Using a spreadsheet to calculate pattern of a polynomial from βs • Spreadsheets are well-suited to conducting repetitive, multistep calculations. • Type in: – Estimated coefficients on the polynomial terms, – Selected values of the independent variable, – Formulas to calculate predicted value of the dependent variable from the βs and values of the independent variable (IV). • Generalize the formulas to apply to all values of the IV. • Create a chart to portray the association between the IV and DV across the observed range of the IV. The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Summary • A regression model involving a polynomial will include separate variables for each term in the polynomial. • The overall shape of the pattern can be calculated by solving the polynomial for values of: – The estimated coefficients on the polynomial terms, and – Selected values of the independent variable across its observed range in the data. • A spreadsheet is an efficient way to calculate and graph the polynomial. The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Suggested resources • Miller, J. E. 2013. The Chicago Guide to Writing about Multivariate Analysis, 2 nd Edition. – Chapter 10, section on polynomials – Appendix D, using a spreadsheet for calculations • Podcast on – Interpreting regression coefficients • Spreadsheet templates – Spreadsheet basics – Solving for a quadratic The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Suggested practice exercises • Study guide to The Chicago Guide to Writing about Multivariate Analysis, 2 nd Edition. – Suggested course extensions for chapter 10 • “Applying statistics and writing” question #7. • “Revising” questions #6 and 9. The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.

Contact information Jane E. Miller, Ph. D jmiller@ifh. rutgers. edu Online materials available at http: //press. uchicago. edu/books/miller/multivariate/index. html The Chicago Guide to Writing about Multivariate Analysis, 2 nd edition.