Calculating Risk of Cost Using Monte Carlo Simulation

Calculating Risk of Cost Using Monte Carlo Simulation with Fuzzy Parameters in Civil Engineering Michał Bętkowski Andrzej Pownuk Silesian University of Technology, Poland

Risk of cost overruns n n We can define risk as possibility of occurrence of loss. There is always the difference between the planned costs and real costs. 2

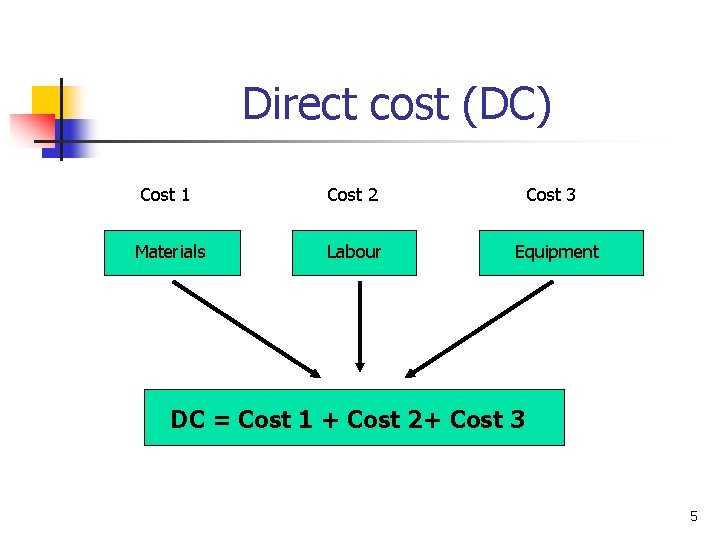
Calculating of cost Direct costs (DC) Direct costs are expenses that are directly linked to the project For example: materials, labour, equipment etc. Indirect costs (IC) Other costs. For example: management costs, cost of insurance etc. 3

Estimating of direct cost (DC) n The project can be decomposed into elements 4

Direct cost (DC) Cost 1 Cost 2 Materials Labour Cost 3 Equipment DC = Cost 1 + Cost 2+ Cost 3 5

Methods of calculating of directional cost n Deterministic n Probabilistic 6

Deterministic methods of calculating costs n - appearance of task is deterministic n - cost of each task is deterministic 7

Calculating Risk in deterministic methods n n Risk in deterministic methods is taken into account as additional constant component of cost. (It is possible to express the risk in percent) 8

Typical problems with deterministic methods of calculating of costs n n n Unknown characteristics of costs (labour, whether), - Alternative tasks, - Additional tasks. 9

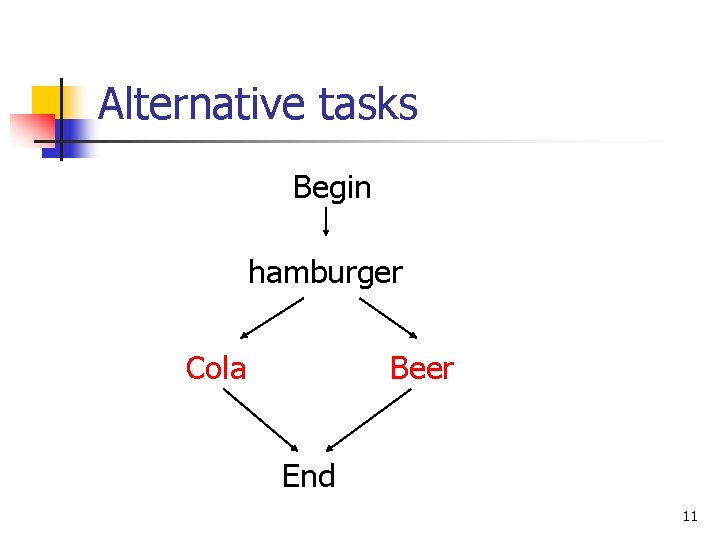
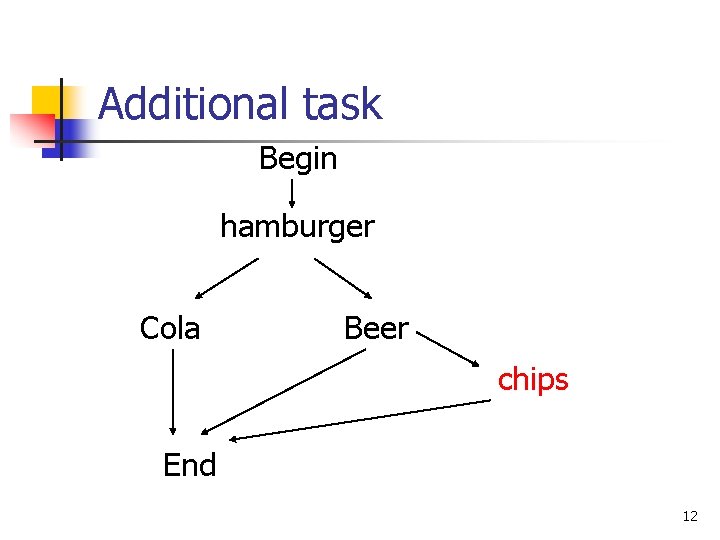
Probabilistic methods n Alternative tasks n Additional task n Changeable costs of tasks 10

Alternative tasks Begin hamburger Cola Beer End 11

Additional task Begin hamburger Cola Beer chips End 12

Changeable costs of tasks n Old car is cheaper than the new one 13

Probabilistic definition of risk - real cost (random variable) - fixed cost 14

Probabilistic definition of risk Probability density function Cumulative distribution function Risk of cost 15

Beta Pert distribution 16

Beta Pert distribution 17

Beta Pert distribution 18

Alternative tasks Cost 1 Cost 2 Cost 3 Total cost = Cost 1 + Cost 2 or Total cost = Cost 1 + Cost 3 19

Existing software - Pert Master, - Risk, - MS Project Etc. 20

Advantages of probabilistic methods n n - Express realistic character of the realization of the process. - Using probabilistic methods it is possible describe random parameters (unpredictable weather, material cost, inaccurate materials estimates) 21

Limitation of pure probabilistic methods n n - unique character of many civil engineering project - different conditions of the realization (weather, geological conditions, geographical region etc. ) Because of that we do not know reliable statistical data 22

Main problem n n It is very difficult to obtain exact values of probabilistic characteristics of the structure For example: m, σ etc. 23

Basic assumption n - According to many experiments parameters of the system can be characterized by typical probability distribution of cost (if we know the data): Normal distribution Beta-Pert distribution Lognormal distribution etc. 24

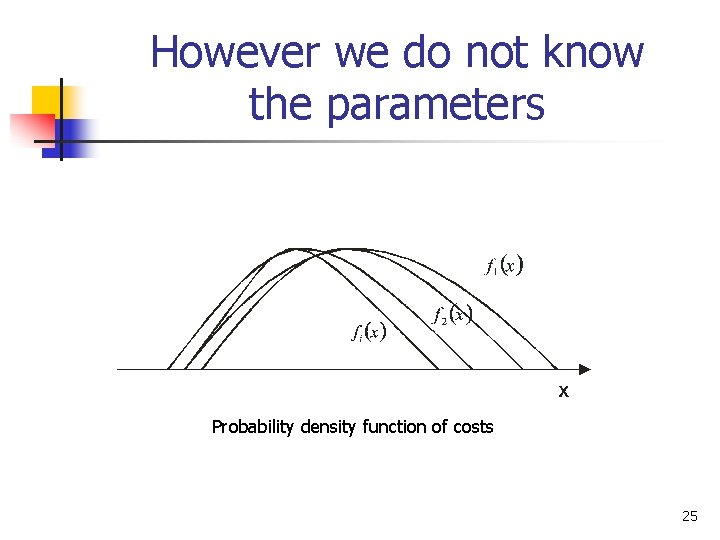
However we do not know the parameters Probability density function of costs 25

What we know? n n n We know deterministic values of costs from the catalogue We have expert knowledge about particular cost (i. e. what happened usually) Sometimes we have some experimental data 26

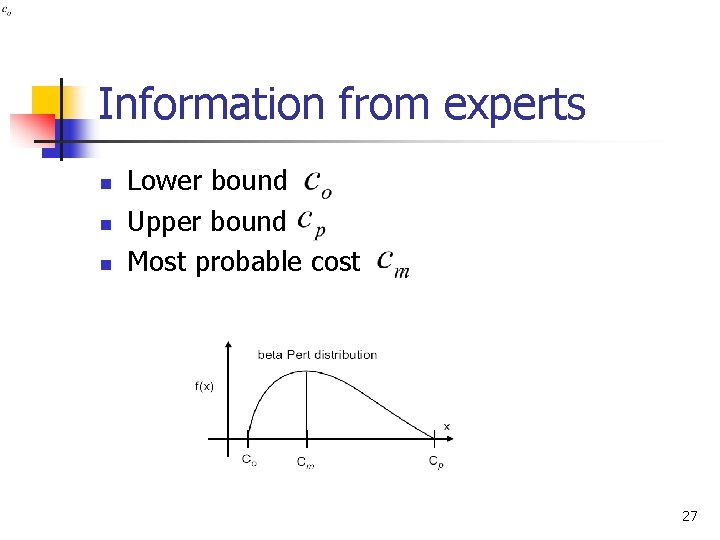
Information from experts n n n Lower bound Upper bound Most probable cost 27

If we have many experts then we can get more information n Lower bound n Upper bound n Most probable cost 28

Fuzzy numbers (clouds) We can also ask experts about confidence intervals for different probability levels (alpha-cuts, degree of membership) 29

Confidence intervals 30

Calculation of fuzzy numbers using the data 31

Advantages of fuzzy sets description (clouds) n n In order to define the worst case (intervals) we do not need many information Confidence intervals can be defined for set valued data (random sets) 32

Dependency problem n It is not a good idea to convert interval probability density function to interval cumulative distribution function (overestimation problem) 33

Dependency problem P-box method consider all possible probability distribution i. e. some of them do not corresponds to any parameters a, b 34

Dependency problem Envelop does not correspond to any combination of parameters 35

Probability density function with fuzzy parameters 36

Application of extension principle 37

- Risk for particular cost - Cumulative distribution function - vector of uncertain parameters 38

Modified extension principle (clouds) 39

Discretization of α-cuts 40

Monte Carlo simulations 41

Advantages of Monte Carlo method n n - it is possible to get full description of probability density function of the results - the method is able to take into account any type of uncertainty and dependency 42

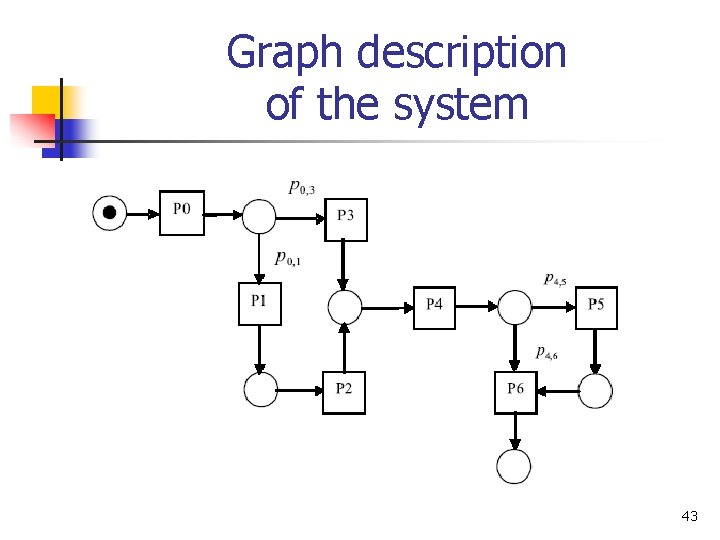
Graph description of the system 43

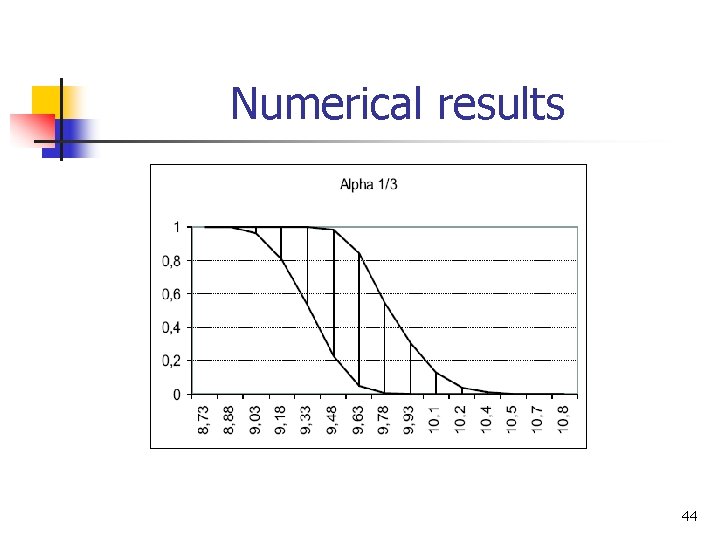
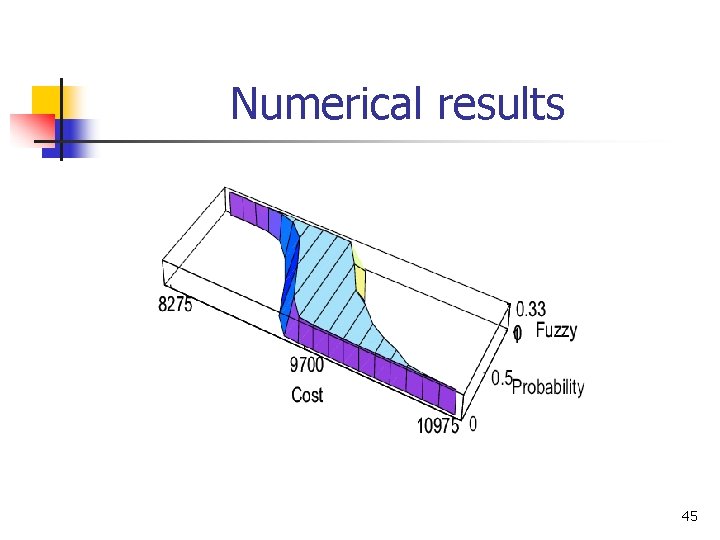
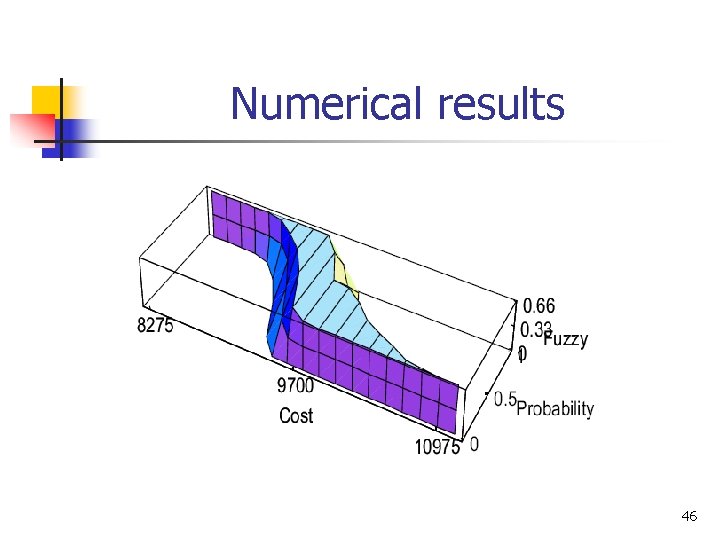
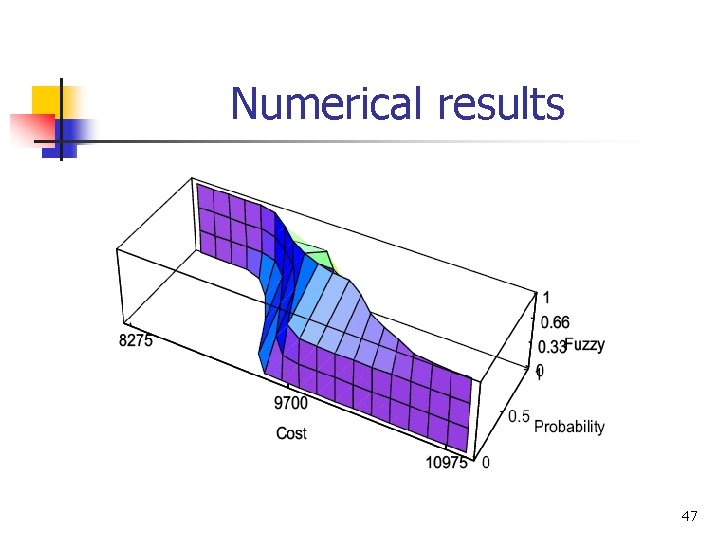
Numerical results 44

Numerical results 45

Numerical results 46

Numerical results 47

Computer implementation of the algorithm n n Algorithm was implemented in C++ language. GSL library was also applied. 48

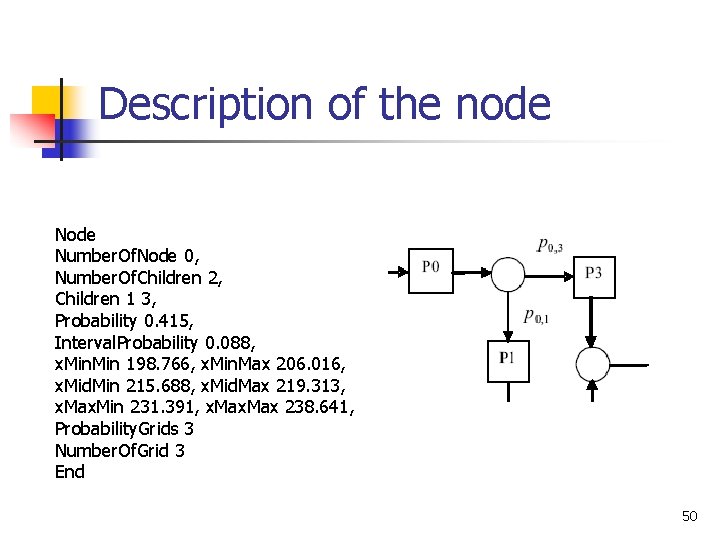
Numerical data for node 0 49

Description of the node Number. Of. Node 0, Number. Of. Children 2, Children 1 3, Probability 0. 415, Interval. Probability 0. 088, x. Min 198. 766, x. Min. Max 206. 016, x. Mid. Min 215. 688, x. Mid. Max 219. 313, x. Max. Min 231. 391, x. Max 238. 641, Probability. Grids 3 Number. Of. Grid 3 End 50

Types of nodes n n n - Normal distribution (with uncertain parameters) - Beta Pert distribution (with uncertain parameters) - constant value - intervals (not implemented) - fuzzy numbers (not implemented) 51

Sum of fuzzy number and probability density function n n Using presented algorithm it is possible to calculate sum of probability density function and fuzzy number (clouds). In calculation one can apply: - min-max extension principle (classical solution - controversial) - new extension principle (recommended, has clear interpretation based on clouds) 52

Results: n n Classic extension principle: - fuzzy probability New extension principle: - fuzzy probability - fuzzy number (confidence intervals, clouds) 53

One more remark about dependency problem Due to nonlinearity alpha cat method is not always good method of transformation of confidence intervals. Because of that we have to check some additional conditions before using this method. 54

Additional information necessary for computation Results Xmin 820, Xmax 1120, Number. Of. Simulations 10000, Number. Of. Classes 20, Number. Of. Grids 3, Distribution. Type 2 End 55

Conclusions Presented method allows estimating the direct cost risk of civil engineering projects in the case when there are no credible data. In presented algorithm the costs can be deterministic, probabilistic, fuzzy number. It is also possible to take into account the cost which is modeled by probability density function with fuzzy parameters. The method shows the relation between the assumed maximal direct costs, the risk of overrun and the uncertainty of the statistical data. 56