Calculating Hrxn There are two ways that Hrxn

Calculating �� Hrxn

There are two ways that ΔHrxn may be calculated from data… 1. Hess’s Law 2. Standard Enthalpies of Formation (ΔH°f)

Hess’s Law

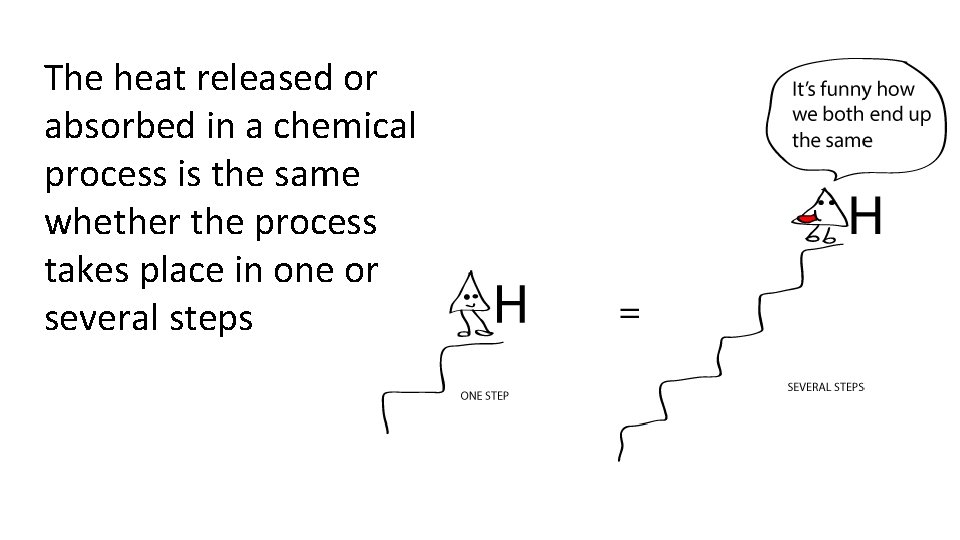
The heat released or absorbed in a chemical process is the same whether the process takes place in one or several steps

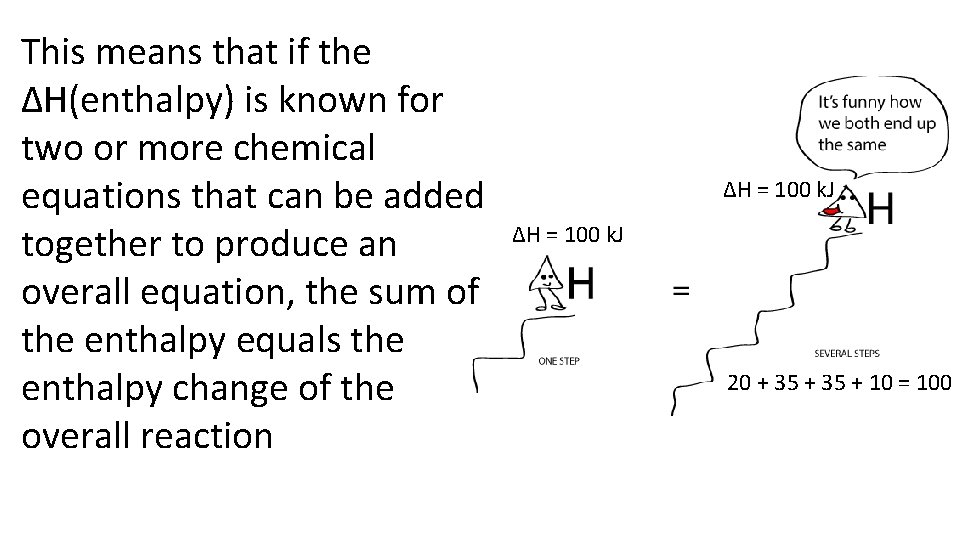
This means that if the ΔH(enthalpy) is known for two or more chemical equations that can be added together to produce an overall equation, the sum of the enthalpy equals the enthalpy change of the overall reaction ΔH = 100 k. J 20 + 35 + 10 = 100

Two rules must be followed to add together the chemical equations: #1 – If you have to reverse the reaction, you must also reverse the sign of the ΔH

#2 – If molar quantities are multiplied by a coefficient then the ΔH must be multiplied by the same coefficient 2 A + B C 4 A + 2 B 2 C ΔH = 100 k. J ΔH = 200 k. J

Calculate the ΔHrxn for the reaction below. H 2 O(g) + C(s) → CO(g) + H 2(g) Use the following sets of reactions. C(s) + ½ O 2(g) → CO(g) H 2(g) + ½ O 2(g) → H 2 O(g) ∆H = -110. 5 k. J ∆H = -241. 8 k. J

Step 1 – Manipulate the equations to get them to match the location (product/reactant) and molar quantity/coefficient of the goal reaction H 2 O(g) + C(s) → CO(g) + H 2(g) C(s) + ½ O 2(g) → CO(g) H 2(g) + ½ O 2(g) → H 2 O(g) ∆H = -110. 5 k. J ∆H = -241. 8 k. J H 2 O – reverse rxn #2 H 2 O(g) → H 2(g) + ½ O 2(g) C – use rxn #1 as is C(s) + ½ O 2(g) → CO(g) CO – taken care of with C H 2 – taken care of with H 2 O ∆H = +241. 8 k. J ∆H = -110. 5 k. J

Step 2 – Cancel compounds/elements (before & after arrow) H 2 O(g) + C(s) → CO(g) + H 2(g) C(s) + ½ O 2(g) → CO(g) H 2(g) + ½ O 2(g) → H 2 O(g) H 2 O – reverse rxn #2 C – use rxn #1 as is ∆H = -110. 5 k. J ∆H = -241. 8 k. J H 2 O(g) → H 2(g) + ½ O 2(g) C(s) + ½ O 2(g) → CO(g) ∆H = +241. 8 k. J ∆H = -110. 5 k. J

Step 3 – Write remaining components as one reaction. This should match the goal equation. H 2 O(g) + C(s) → CO(g) + H 2(g) C(s) + ½ O 2(g) → CO(g) H 2(g) + ½ O 2(g) → H 2 O(g) H 2 O – reverse rxn #2 C – use rxn #1 as is ∆H = -110. 5 k. J ∆H = -241. 8 k. J H 2 O(g) → H 2(g) + ½ O 2(g) C(s) + ½ O 2(g) → CO(g) ∆H = +241. 8 k. J ∆H = -110. 5 k. J H 2 O(g) + C(s) → CO(g) + H 2(g)

Step 4 – Find the sum of the ΔH to get the ΔH for the goal reaction. H 2 O(g) + C(s) → CO(g) + H 2(g) C(s) + ½ O 2(g) → CO(g) H 2(g) + ½ O 2(g) → H 2 O(g) H 2 O – reverse rxn #2 C – use rxn #1 as is ∆H = -110. 5 k. J ∆H = -241. 8 k. J H 2 O(g) → H 2(g) + ½ O 2(g) C(s) + ½ O 2(g) → CO(g) H 2 O(g) + C(s) → CO(g) + H 2(g) ∆H = +241. 8 k. J ∆H = -110. 5 k. J ∆H = +131. 3 k. J

Calculate the ΔHrxn for the reaction below. 4 NH 3(g) + 5 O 2(g) 4 NO(g) + Use the following sets of reactions. N 2(g) + O 2(g) N 2(g) + 3 H 2(g) 2 H 2(g) + O 2(g) 2 NO(g) 2 NH 3(g) 2 H 2 O(g) H = 180. 6 H = -91. 8 k. J H = -483. 7 k. J

Step 1 4 NH 3(g) + N 2(g) + O 2(g) N 2(g) + 3 H 2(g) 2 H 2(g) 5 O 2(g) + O 2(g) 2 NO(g) 2 NH 3(g) 2 H 2 O(g) 4 NO(g) H = 180. 6 H = -91. 8 k. J H = -483. 7 k. J NH 3 – reverse rxn #2 & 2 x 4 NH 3(g) 2 N 2(g) + 6 H 2(g) ΔH = +183. 6 k. J NO – 2 x rxn #1 2 N 2(g) + 2 O 2 4 NO(g) H 2 O – 3 x rxn #3 ΔH = +361. 2 k. J 6 H 2(g) + 3 O 2(g) 6 H 2 O(g) ΔH = -1451. 1 k. J

Step 2 4 NH 3(g) + 5 O 2(g) 4 NO(g) NH 3 – 4 NH 3(g) 2 N 2(g) + 6 H 2(g) ΔH = +183. 6 k. J NO – 2 N 2(g) + 2 O 2 4 NO(g) ΔH = +361. 2 k. J H 2 O – 6 H 2(g) + 3 O 2(g) 6 H 2 O(g) ΔH = -1451. 1 k. J +

Steps 3 & 4 4 NH 3(g) + 5 O 2(g) 4 NO(g) NH 3 – 4 NH 3(g) 2 N 2(g) + 6 H 2(g) ΔH = +183. 6 k. J NO – 2 N 2(g) + 2 O 2 4 NO(g) ΔH = +361. 2 k. J H 2 O – 6 H 2(g) + 3 O 2(g) 6 H 2 O(g) 4 NH 3(g) + 5 O 2(g) → 4 NO(g) + 6 H 2 O(g) ΔH = -1451. 1 k. J ∆H = -906. 3 k. J +

Calculate the ΔHrxn for the reaction below. 4 C(s) + 5 H 2(g) → C 4 H 10(g) Use the following sets of reactions. C 4 H 10(g) + 6 ½ O 2(g) → 4 CO 2(g) + 5 H 2 O(g) ∆H= -2657. 4 k. J/mol C(s) + O 2(g) → CO 2(g) ∆H= -393. 5 k. J/mol H 2(g) + ½O 2(g) → H 2 O(g) ∆H= -241. 8 k. J/mol

Step 1 4 C(s) + 5 H 2(g) → C 4 H 10(g) + 6 ½ O 2(g) → 4 CO 2(g) + 5 H 2 O(g) ∆H= -2657. 4 k. J/mol C(s) + O 2(g) → CO 2(g) ∆H= -393. 5 k. J/mol H 2(g) + ½O 2(g) → H 2 O(g) ∆H= -241. 8 k. J/mol C – 4 x rxn #2 H 2 – 5 x rxn #3 4 C(s) + 4 O 2(g) 4 CO 2(g) 5 H 2(g) + 2½O 2(g) 5 H 2 O(g) ΔH = -1574 k. J ΔH = -1209 k. J C 4 H 10 – reverse rxn #1 4 CO 2(g) + 5 H 2 O(g) C 4 H 10(g) + 6 ½ O 2(g) ΔH = +2657. 4 k. J

Step 2 4 C(s) + 5 H 2(g) → C 4 H 10(g) C– 4 C(s) + 4 O 2(g) 4 CO 2(g) ΔH = -1574 k. J H 2 – 5 H 2(g) + 2½O 2(g) 5 H 2 O(g) ΔH = -1209 k. J C 4 H 10 – 4 CO 2(g) + 5 H 2 O(g) C 4 H 10(g) + 6 ½ O 2(g) ΔH = +2657. 4 k. J

Step 3 & 4 4 C(s) + 5 H 2(g) → C 4 H 10(g) C– 4 C(s) + 4 O 2(g) 4 CO 2(g) ΔH = -1574 k. J H 2 – 5 H 2(g) + 2½O 2(g) 5 H 2 O(g) ΔH = -1209 k. J C 4 H 10 – 4 CO 2(g) + 5 H 2 O(g) C 4 H 10(g) + 6 ½ O 2(g) ΔH = +2657. 4 k. J 4 C(s) + 5 H 2(g) → C 4 H 10(g) ∆H = -125. 6 k. J

Standard Enthalpy of Formation (ΔH°f) aka heat of formation

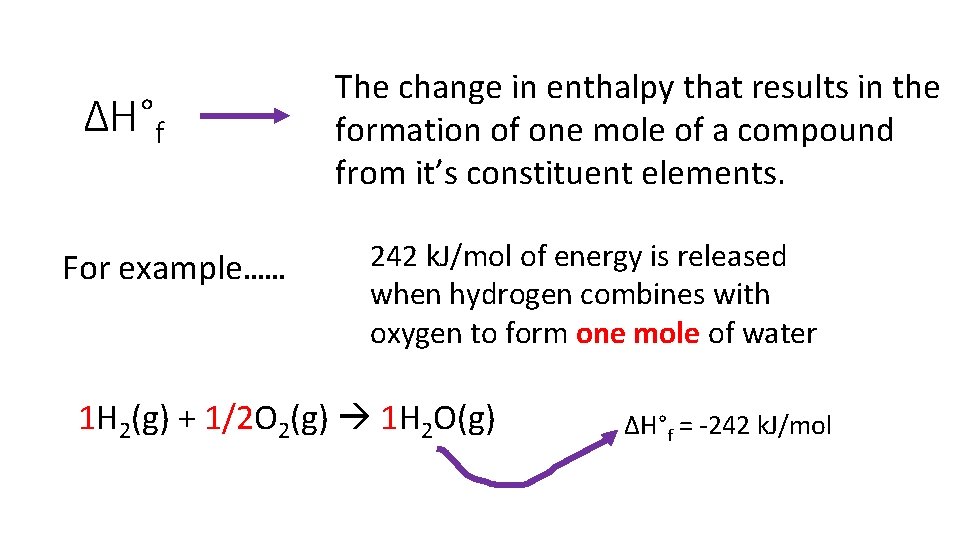
ΔH°f For example…… The change in enthalpy that results in the formation of one mole of a compound from it’s constituent elements. 242 k. J/mol of energy is released when hydrogen combines with oxygen to form one mole of water 1 H 2(g) + 1/2 O 2(g) 1 H 2 O(g) ΔH°f = -242 k. J/mol

Compound/Element ΔH°f are known quantities for ALL elements, including diatomics Hf = 0 k. J/mol H 2 (g) O 2 (g) H 2 O (l) H 2 O 2 (l) NH 3 (g) NH 4 Cl (s) HCl (g) Fe. S (s) Fe 2 O 3 (s) SO 2 (g) Na. HCO 3 (s) Na 2 CO 3 (s) CO 2 (g) H 2 S (g) H f k. J/mol 0 0 -242 -286 -188 -46 -314 -92 -102 -824 -297 -951 -1131 -394 -21

The enthalpy of a reaction (ΔHrxn) can be calculated from the heat of formation (ΔHf) of the substances in the reaction. “Sum of Reactants” Hrxn = n Hf°products – m Hf° reactants “Sum of Products” ** n and m are the stoichiometric coefficients ** ** you have to have a balanced equation **

Calculate the ΔHrxn for the reaction below. 2 CO + O 2 2 CO 2 Hf CO = -110. 5 k. J, Hf CO 2 = -393. 5 k. J Hrxn = n Hf°products – m Hf° reactants = (2(-393. 5 k. J)) – (2(-110. 5 k. J) + 0 k. J) = -787. 0 k. J + 221. 0 k. J Hrxn = -566. 0 k. J