Calculating Area on Topographic Maps Area of a



- Slides: 7

Calculating Area on Topographic Maps

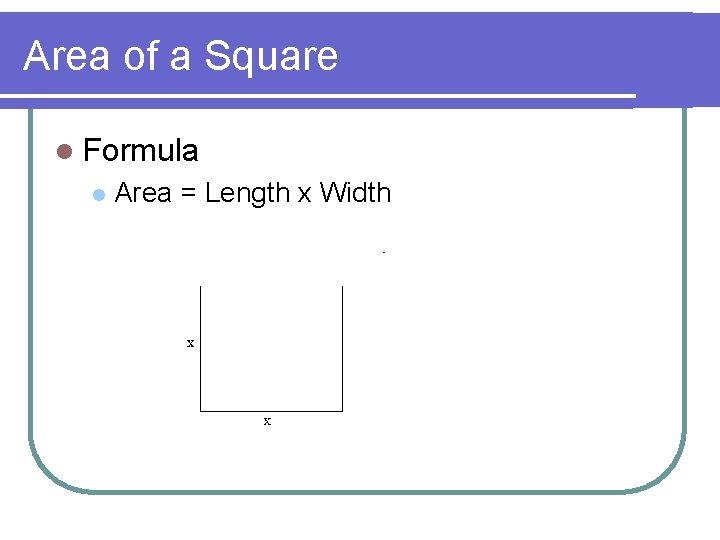
Area of a Square l Formula l Area = Length x Width

Calculating the area of an even boundary l A map with a scale of 1: 50 000. The length of this map is 5 cm and the width is 3 cm. Calculate the area represented by the map. l Convert the length and width into what they represent in reality before using the formula*. Scale 1: 50 000 - therefore each cm on the map represents 0. 5 km in reality l Length: 5 cm x 0. 5 km = 2. 5 km l Width: 3 cm x 0. 5 km = 1. 5 km l Area = Length x Width = 2. 5 km x 1. 5 km = 3. 75 sq. km

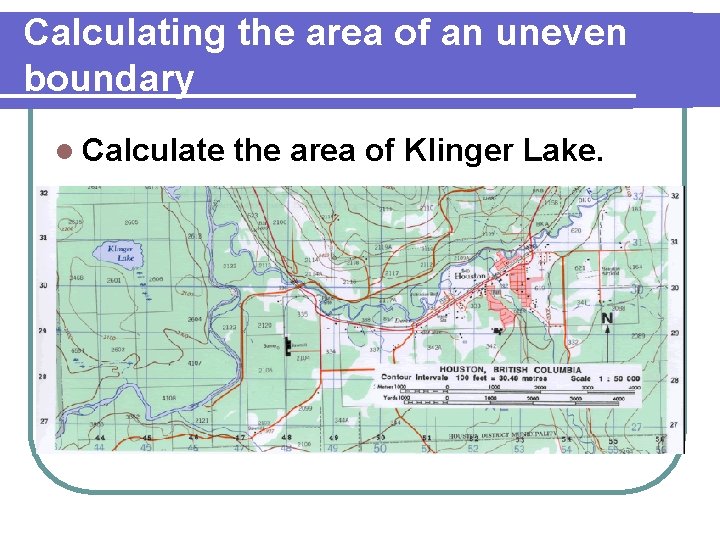
Calculating the area of an uneven boundary l Calculate the area of Klinger Lake.

How to do it… Step 1: Work out the area of one grid square on the map. l Scale of this map: 1: 50 000, therefore each cm represents 0. 5 km l Length: 2 cm x 0. 5 km = 1. 0 km l Width: 2 cm X 0. 5 km = 1. 0 km l Area of One Grid Square = 1. 0 km x 1. 0 km = 1. 0 sq. km Step 2: Determine the number of squares that the object occupies. l Klinger Lake occupies a total of about 0. 5 of a grid square. Step 3: Multiply the number of grid squares that the object occupies by the area of one grid square. l Hence, 0. 5 of a square x 1. 0 sq. km = 0. 5 sq. km which is the area of Klinger Lake.

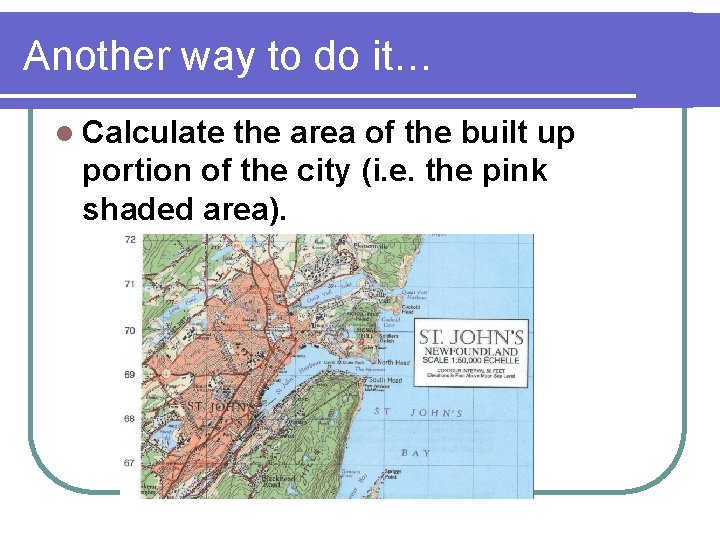
Another way to do it… l Calculate the area of the built up portion of the city (i. e. the pink shaded area).

Working with Percentages… Step 1: Work out the area of one grid square on the map. l It is the same as the previous map: 1. 0 sq. km. Step 2: Determine the number of squares that the object occupies. l In this situation, one could go from grid square to grid square determing how much the built up area occupies each square. i. e. 0. 1 of a grid square (5866) + 0. 4 (5966) + 0. 7 (5967) + 0. 7 (6067) + 0. 03 (5868) + 0. 5 (5968) + 1. 0 (6068) + 0. 25 (6168) + 0. 2 (5869) + 0. 6 (5969) + 1. 0 (6069) + 0. 85 (6169) + 0. 2 (6269) + 0. 8 (6070) + 0. 85 (6170) + 0. 2 (6270) + 0. 2 (6071) + 0. 4 (6171) = 8. 98 squares Step 3: Multiply the number of grid squares that the object occupies by the area of one grid square. l Hence, 8. 98 squares x 1. 0 sq. km = 8. 98 sq. km which is the area of downtown St. John's.