Calcolo delle variazioni Modellistica e Ottimizzazione di Sistemi

Calcolo delle variazioni Modellistica e Ottimizzazione di Sistemi e Processi Energetici K. D. Bizon

Ottimizzazione in spazi funzionali: il calcolo variazionale • Si può generalizzare il concetto di ottimizzazione, costruendo un cosiddetto funzionale, ossia un’espressione a valori in , l’equivalente concettuale della funzione obiettivo, che dipende non più da un certo numero di parametri di progetto, ma da una o più funzioni incognite. • Tali funzionali possono per esempio essere formulati come integrali che coinvolgono una funzione incognita e le sue derivate. L’interesse è per le funzioni estremali: quelle cioè che rendono massimo o minimo il valore del funzionale. • Come per i problemi di minimizzazione in spazi a dimensione finita, anche in quest’ambito esistono condizioni necessarie per l’esistenza di estremi, che corrispondono a una condizione di stazionarietà per il funzionale. L’analisi delle piccole variazioni attorno ad una presunta soluzione porta a una condizione necessaria del primo ordine.

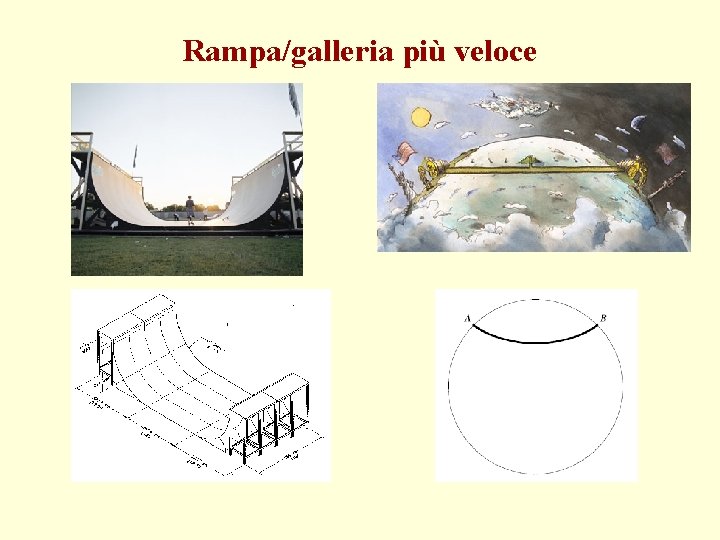
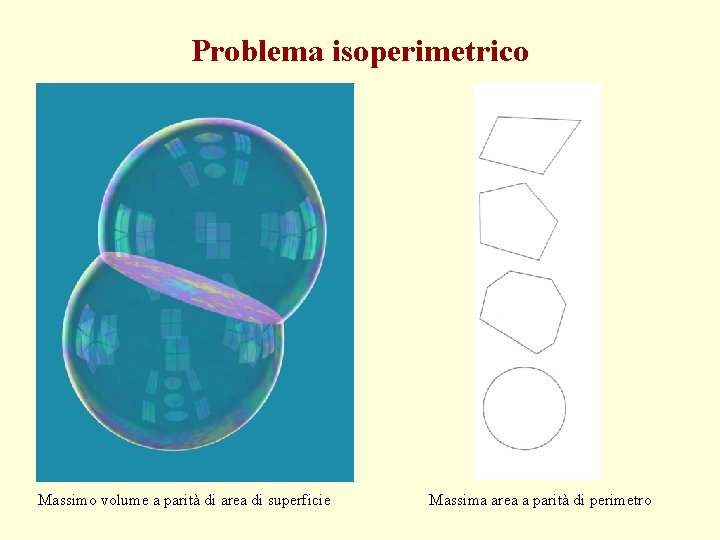
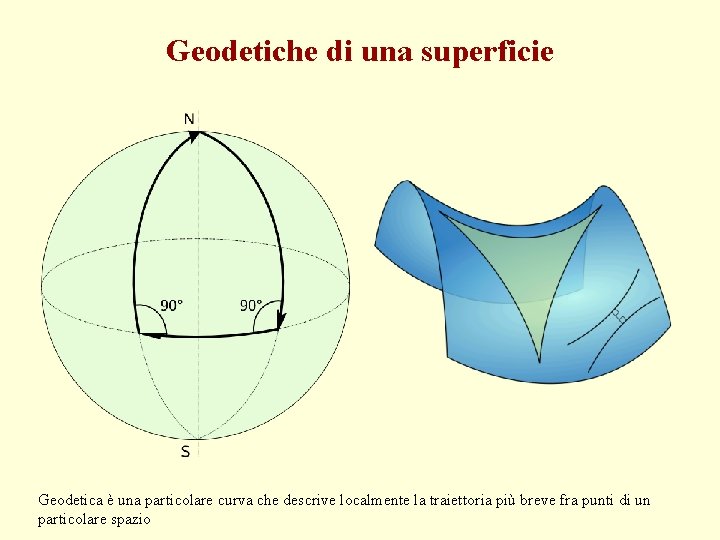
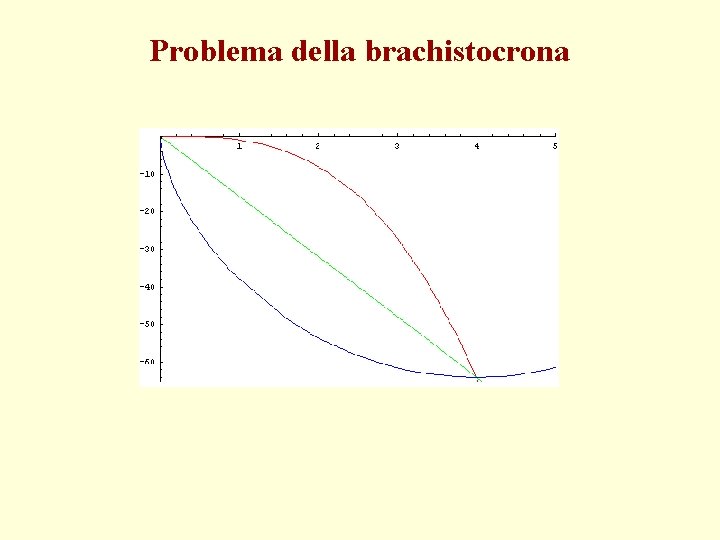
I problemi classici di calcolo delle variazioni • Tra i grandi problemi passati alla storia della matematica, vale la pena citarne alcuni, oltreché per il loro interesse soprattutto geometrico e fisico, per il ruolo che hanno avuto nello sviluppo del calcolo delle variazioni. • Nel problema isoperimetrico ci si chiede quale figura piana o spaziale renda massima l’area o il volume, a seconda della dimensione, a parità di perimetro o di area della superficie che lo racchiude. • Un altro problema interessante è quello della ricerca delle geodetiche di una superficie, che sono le curve di minima lunghezza, di estremi assegnati e giacenti su di essa. Per la sfera le soluzioni sono gli archi di cerchio massimo. • Il celebre problema della brachistocrona venne posto nel 1696 da Jean Bernoulli. Si tratta della traiettoria prestabilita liscia lungo la quale deve scivolare un punto materiale pesante, con posizioni iniziale e finale assegnate, affinché il tempo impiegato per la discesa sia minimo.

Rampa/galleria più veloce

Problema isoperimetrico Massimo volume a parità di area di superficie Massima area a parità di perimetro

Geodetiche di una superficie Geodetica è una particolare curva che descrive localmente la traiettoria più breve fra punti di un particolare spazio

Problema della brachistocrona

Calcolo delle variazioni • Lo strumento chiave del calcolo delle variazioni classico è l’equazione di Eulero-Lagrange. • Nella sua forma più semplice, il calcolo delle variazioni consiste nel minimizzare il cosiddetto integrale d'azione: al variare della funzione y (x) fra tutte quelle che soddisfano le condizioni y (x 1) = y 1 ed y (x 2) = y 2. Si cerca dunque una funzione y = y (x) (x 1 x x 2 ) che collega i due punti (x 1 , y 1 ) e (x 2 , y 2 ) e che minimizza l'integrale d'azione I.

Calcolo delle variazioni Nella sua forma più semplice, il calcolo delle variazioni consiste nel minimizzare il cosiddetto integrale d'azione: al variare della funzione y(x) fra tutte quelle che soddisfano le condizioni: y (x 1) = y 1 ; y(x 2) = y 2. Questo appena enunciato si chiama problema fondamentale del calcolo delle variazioni. Si cerca dunque una funzione y = y(x) , (x 1 x x 2 ) che collega i due punti (x 1 , y 1 ) e (x 2 , y 2 ) e che minimizza l'integrale I.

Calcolo delle variazioni: l’equazione di Eulero-Lagrange Supponiamo che f sia di classe C 1 nelle tre variabili x, y ed y´, e consideriamo le due funzioni y(x) ed Y(x) = y(x) , entrambe passanti per i due punti (x 1 , y 1 ) e (x 2 , y 2 ), dove è un parametro. Poiché y(x 1) = Y(x 1) ed y(x 2) = Y(x 2) , allora (x 1) = (x 2) = 0 ; per il resto, la funzione (x) è arbitraria. Il termine (x) rappresenta la variazione di y(x). Noi vogliamo determinare quella y(x) per la quale il funzionale I ha un estremo relativo, e dunque quella y(x) che, comunque perturbata dalla variazione (x), con piccolo, lascia stazionario il valore del funzionale:

Calcolo delle variazioni: l’equazione di Eulero-Lagrange Calcoliamo quindi la derivata rispetto ad del funzionale I. Applicando la regola di derivazione delle funzioni composte, si ha: Scomponiamo l’integrale in somma di integrali ed integriamo il secondo per parti:

Calcolo delle variazioni: l’equazione di Eulero-Lagrange Poiché (x 1) = (x 2) = 0, l’integrale del fattore finito si annulla e dunque, portando a fattor comune, si ha: Dato che (x) è una funzione arbitraria, l’integrale è nullo se e solo se è identicamente nulla la quantità in parentesi. Di conseguenza, la derivata rispetto ad del funzionale I si annulla se e solo se y(x) è soluzione dell’equazione (detta di Eulero-Lagrange):

Calcolo delle variazioni: l’identità di Beltrami Se la funzione f è esplicitamente indipendente da x, si può dimostrare che la soluzione del problema variazionale soddisfa una forma particolare dell’equazione di Eulero-Lagrange, detta Identità di Beltrami: dove C è una costante.

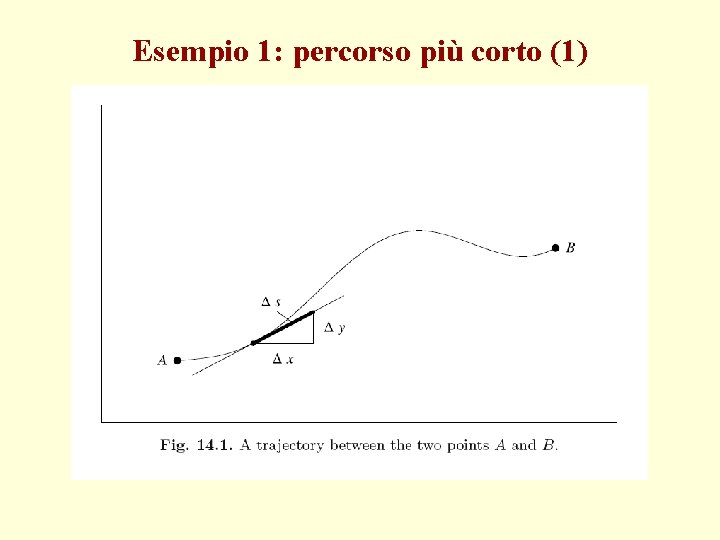
Esempio 1: percorso più corto (1)

Esempio 1: percorso più corto (2)

Esempio 1: percorso più corto (3)

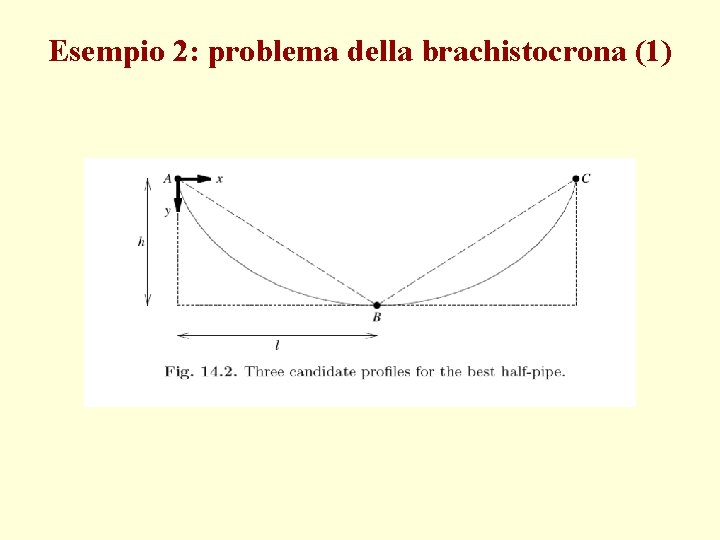
Esempio 2: problema della brachistocrona (1)

Esempio 2: problema della brachistocrona (2)

Esempio 2: problema della brachistocrona (3)

Esempio 2: problema della brachistocrona (4)

Esempio 2: problema della brachistocrona (5)

Esempio 2: problema della brachistocrona (8)

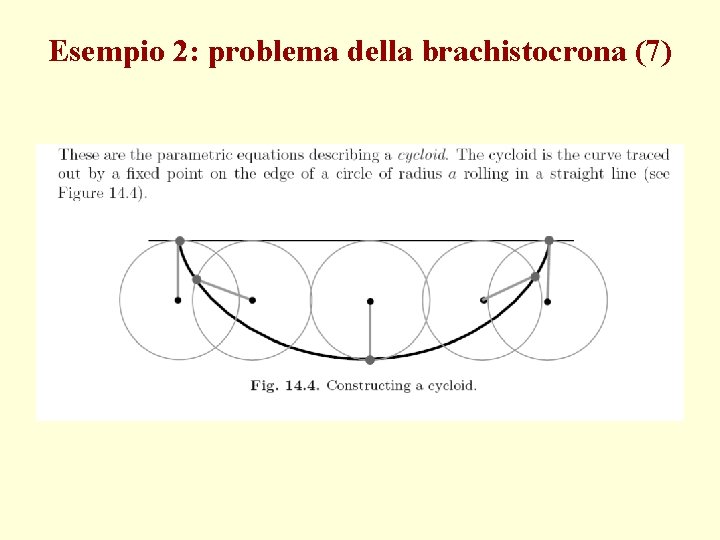
Esempio 2: problema della brachistocrona (7)

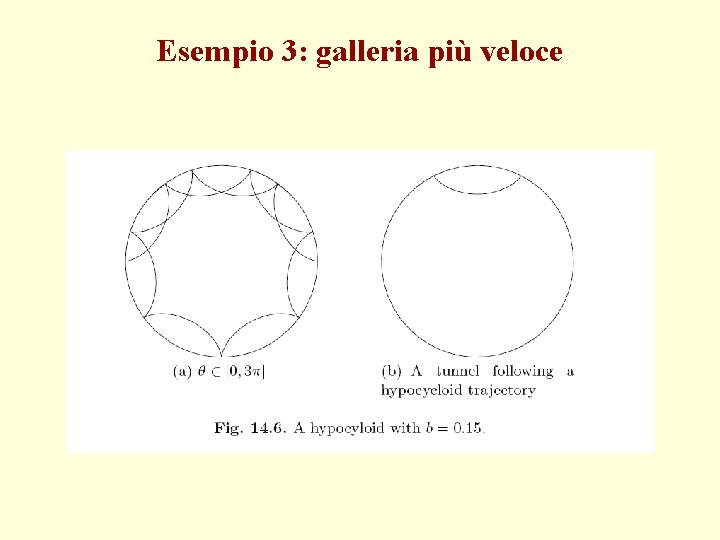
Esempio 3: galleria più veloce

Problema isoperimetrico (1)

Problema isoperimetrico (2)

Esempio 5: cavo sospeso (1)

Esempio 5: cavo sospeso (2)

Esempio 5: cavo sospeso (3)

Metodi numerici • Metodo di Eulero • Metodo di Ritz • Metodo di Kantorowicz (per più variabili)

Metodo di Ritz (1)

Metodo di Ritz (2)

Metodo di Ritz (3)

Metodo di Ritz: esempio (1)

Metodo di Ritz: esempio (2)

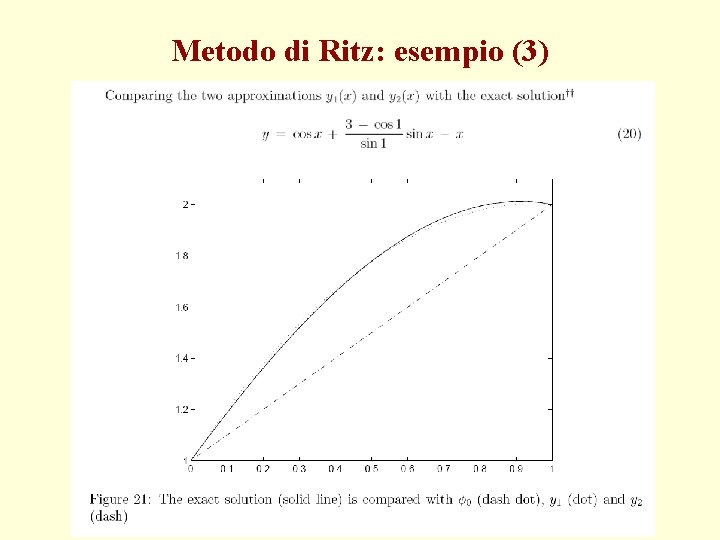
Metodo di Ritz: esempio (3)

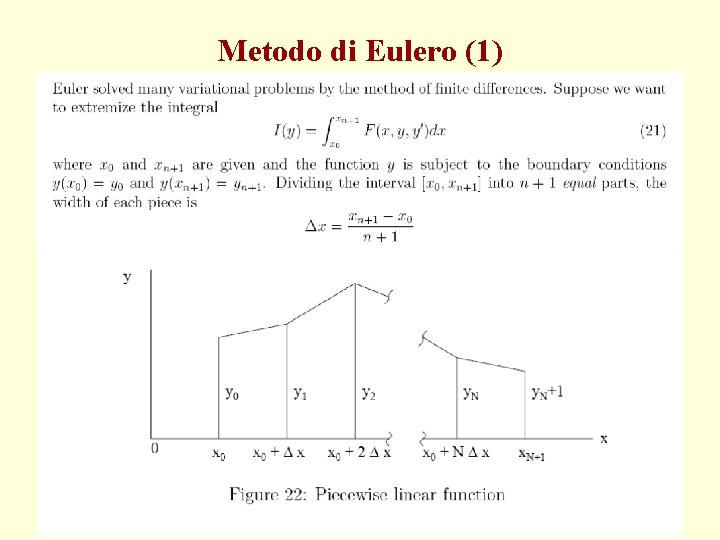
Metodo di Eulero (1)

Metodo di Eulero (1)

Metodo di Eulero (3)

Metodo di Eulero: esempio (1)

Metodo di Eulero: esempio (2)

Metodo di Eulero: esempio (3)

Metodo di Eulero: esempio (4)

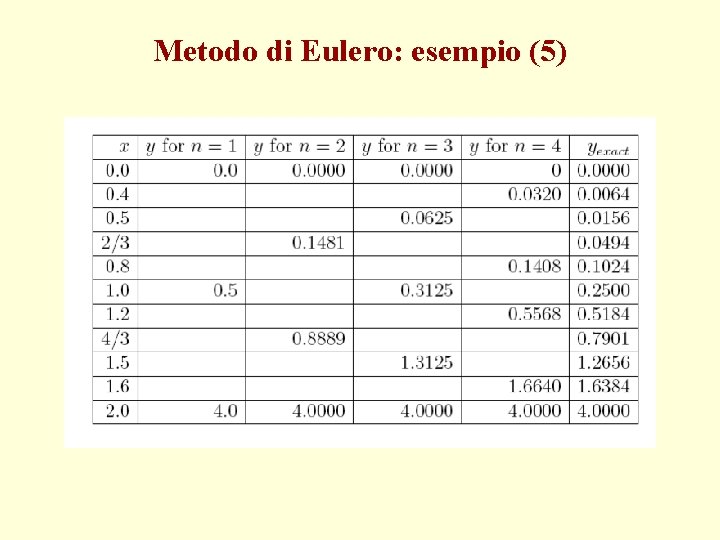
Metodo di Eulero: esempio (5)