C Programming Review 1 Overview Integer Errors Representation

C Programming Review 1

Overview • Integer Errors • Representation, conversion, operations • Common misunderstandings, sources of error • • • Strings Arrays Pointers Dynamic memory allocation Memory Errors 2

Integer Representation 3

Motivation • Integers represent a growing and underestimated source of vulnerabilities in C and C++ programs • Integer range checking has not been systematically applied in the development of most C and C++ software • Outline 1. 2. 3. 4. Integer representation Integer conversions Integer operations Mitigation See “Secure Coding in C and C++”, 2 nd edition, Robert Seacord, Chapter 5; CERT Standard, Computer Systems A Programmers Perspective, Bryant & O’Hallaron, Ch. 2 “Unverified” link to Seacord: http: //ptgmedia. pearsoncmg. com/images/0321335724/samplechapter/seacord_ch 05. pdf 4

1) Integer Representation • Signed-magnitude • One’s complement • Two’s complement • These integer representations vary in how they represent negative numbers 5

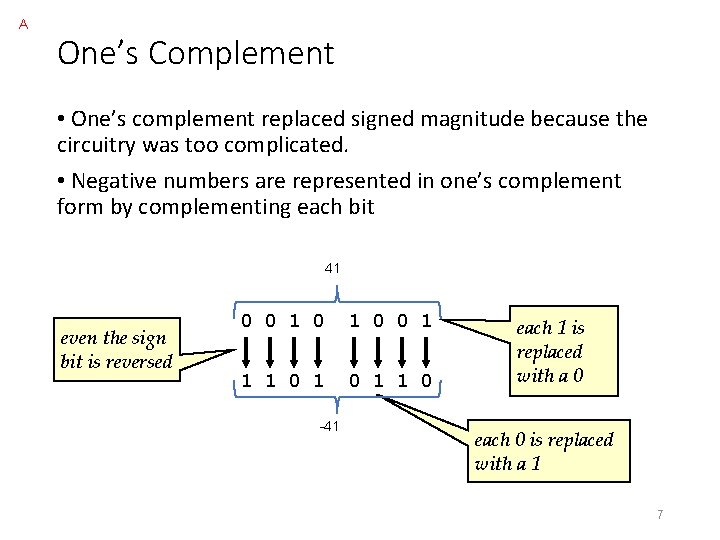
Signed-magnitude Representation • Uses the high-order bit to indicate the sign • 0 for positive • 1 for negative • remaining low-order bits indicate the magnitude of the value Signed-magnitude representation of 41 and -41. 6

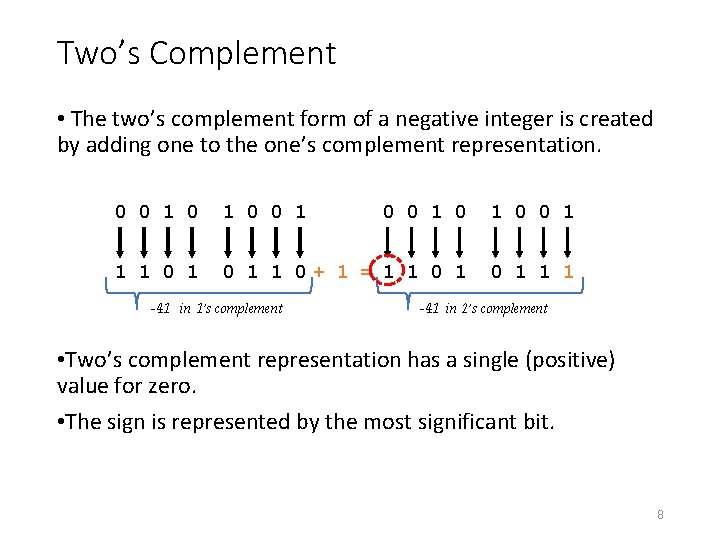
A One’s Complement • One’s complement replaced signed magnitude because the circuitry was too complicated. • Negative numbers are represented in one’s complement form by complementing each bit 41 even the sign bit is reversed 0 0 1 1 1 0 -41 each 1 is replaced with a 0 each 0 is replaced with a 1 7

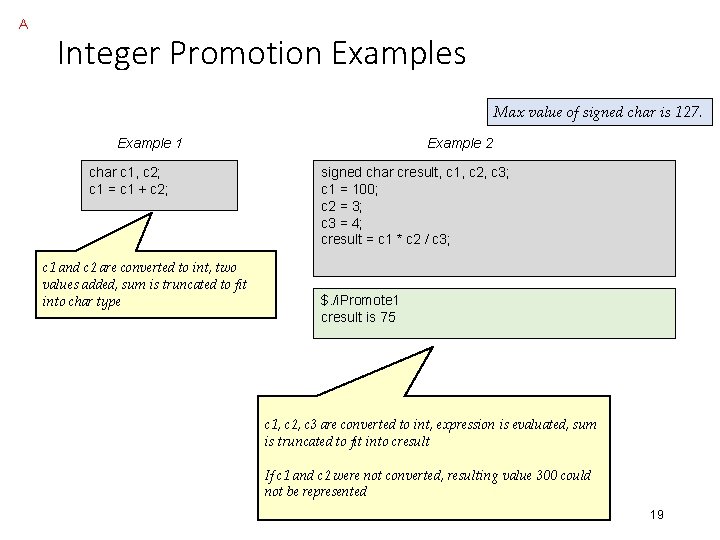
Two’s Complement • The two’s complement form of a negative integer is created by adding one to the one’s complement representation. 0 0 1 0 1 0 0 1 1 1 0+ 1 = 1 1 0 1 1 1 -41 in 1’s complement -41 in 2’s complement • Two’s complement representation has a single (positive) value for zero. • The sign is represented by the most significant bit. 8

Signed and Unsigned Types • Integers in C and C++ are either signed or unsigned. • For each signed type there is an equivalent unsigned type. • Two’s complement on N bit integer: • Signed range is –(2 N-1) to 2(N-1) - 1 • Unsigned range is 0 to 2 N-1 * • limits. h defines compiler and platform-specific limits (e. g. UINT_MAX, INT_MIN, etc. ) *On Linux systems, header files usually in /usr/include/. 9

Example Integer Ranges (8 bits) (16 bits) = -215 = 215 - 1 (16 bits) 216 - 1 = 10

Guaranteed Ranges for C Integral Data C Type Minimum Maximum [signed] char -128 127 unsigned char 0 255 short -32768 32767 unsigned short 0 65535 int -2147483648 2147483647 unsigned int 0 4294967295 long -2147483648 (-9223372036854775808) 2147483647 (9223372036854775807) unsigned long 0 4294967295 (18446744073709551615) Int 32_t -2147483648 2147483647 uint 32_t 0 4294967295 int 64_t -9223372036854775808 9223372036854775807 uint 64_t 0 18446744073709551615 32 -bit and 64 -bit are the same except where noted. Values in parentheses note 64 bit values where they are different from 32 -bit 11

Integer Types • Standard integers include the following types in nondecreasing length order: signed char, short int, long int • The following types are used for special purposes • ptrdiff_t is the signed integer type of the result of subtracting two pointers • size_t is the unsigned result of the sizeof operator • wchar_t is an integer type whose range of values can represent distinct codes for all members of the largest extended character set specified among the supported locales 12

Signed/Unsigned Characters • The type char can be signed or unsigned. • When a signed char with its high bit set is saved in an integer, the result is a negative number. • Use unsigned char for buffers, pointers, and casts when dealing with character data that may have values greater than 127 (0 x 7 f). 13

A Example 1: Signed to Unsigned int main(){ int i = -3; unsigned short u; u=i; printf("u = %hun", u); } -3 is: 11111111 11111101 Bit pattern preserved, truncated. 11111101 is MAX (65535) – 2 /. $sign u = 65533 14

Example 2: Unsigned to Signed int main(){ unsigned short int u; short int i; printf("unsigned short int is %d bytesn", sizeof(unsigned short int)); printf("short int is %d bytesn", sizeof(short int)); u=32768; // 2^15 = 10. . . 00 base 2 Bit pattern is preserved. i=u; printf("i = %dn", i); u=65535; // 2^16 – 1 = 11. . . 11 Bit pattern is preserved. i=u; printf("i=%dn", i); } $. /truncation unsigned short int is 2 bytes i = -32768 i=-1 15

Example 3 See limits. h. Defines limits the implementation imposes on application. #include <limits. h> int main() } int i; unsigned int j; i = INT_MAX; // 2, 147, 483, 647 = 231 - 1 i++; printf("INT_MAX=%d, i=%dn", INT_MAX, i; ( j = UINT_MAX; // 4, 294, 967, 295 = 232 - 1; j++; printf("UNIT_MAX=%u, j=%un", UINT_MAX, j; ( i = INT_MIN; // -2, 147, 483, 648 = -231 i--; printf("INT_MIN=%d, i = %dn", INT_MIN, i; ( j = 0; j; - printf("j = %un", j; ( $. /overflow { INT_MAX=2147483647, i=-2147483648 UNIT_MAX=4294967295, j=0 INT_MIN=-2147483648, i = 2147483647 j = 4294967295 16

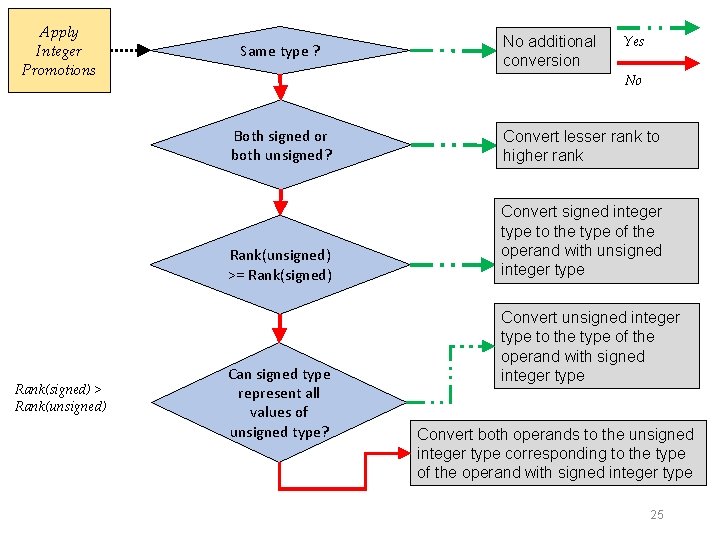
2) Integer Conversions • Type conversions occur explicitly in C and C++ as the result of a cast or implicitly as required by an operation x = (float)10/3 • Implicit conversions are a consequence of the C language ability to perform operations on mixed types • Conversions can lead to lost or misinterpreted data • C 99 rules define how C compilers handle conversions i. Integer promotions: performed automatically ii. Integer conversion rank: used by usual arithmetic conversions iii. Usual arithmetic conversions: rules for conversion after promotion 17

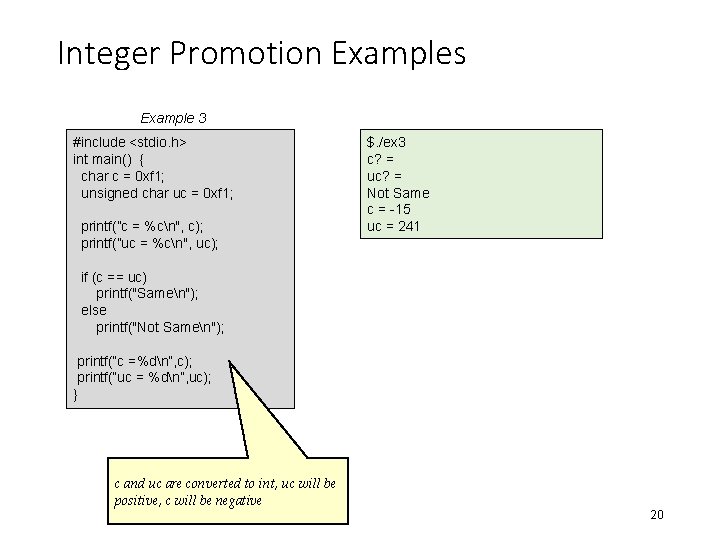
2. i) Integer Promotions • Integer types smaller than int are promoted when an operation is performed on them • If all values of original type can be represented as an int, value of smaller type converted to int; otherwise, converted to unsigned int • Integer promotions are applied as part of the usual arithmetic conversions to • certain argument expressions • operands of the unary +, -, and ~ operators • operands of the shift operators 18

A Integer Promotion Examples Max value of signed char is 127. Example 1 char c 1, c 2; c 1 = c 1 + c 2; c 1 and c 2 are converted to int, two values added, sum is truncated to fit into char type Example 2 signed char cresult, c 1, c 2, c 3; c 1 = 100; c 2 = 3; c 3 = 4; cresult = c 1 * c 2 / c 3; $. /i. Promote 1 cresult is 75 c 1, c 2, c 3 are converted to int, expression is evaluated, sum is truncated to fit into cresult If c 1 and c 2 were not converted, resulting value 300 could not be represented 19

Integer Promotion Examples Example 3 #include <stdio. h> int main() { char c = 0 xf 1; unsigned char uc = 0 xf 1; printf(”c = %cn", c); printf(”uc = %cn", uc); $. /ex 3 c? = uc? = Not Same c = -15 uc = 241 if (c == uc) printf("Samen"); else printf("Not Samen"); printf(“c =%dn”, c); printf(“uc = %dn”, uc); } c and uc are converted to int, uc will be positive, c will be negative 20

2. ii) Integer Conversion Rank • Each integer type has a conversion rank • Used to determine how conversions are performed • Rules for ranking defined by C standard 1. No two different signed integer types shall have the same rank, even if they have the same representation. 2. The rank of a signed integer type shall be greater than the rank of any signed integer type with less precision. 3. The rank of long int shall be greater than the rank of long int, which shall be greater than the rank of int, which shall be greater than the rank of short int, which shall be greater than the rank of signed char. 4. The rank of any unsigned integer type shall equal the rank of the corresponding signed integer type, if any. 5. The rank of char shall equal the rank of signed char and unsigned char 21

Integer Conversion Rank 6. The rank of any standard integer type is greater than the rank of any extended integer type with the same width. 7. The rank of any extended signed integer type relative to another extended signed integer type with the same precision is implementation defined but still subject to the other rules for determining the integer conversion rank. 8. For all integer types T 1, T 2, and T 3, if T 1 has greater rank than T 2 and T 2 has greater rank than T 3, then T 1 has greater rank than T 3. Operand Type long int, unsigned long int, unsigned int Higher Rank short int, unsigned short int char, signed char, unsigned char Conversion ranks for integer types 22

2. iii) Usual Arithmetic Conversions • Usual arithmetic conversions are rules to yield a common type when • both operands of binary operator balanced to a common type or • second and third operands of the conditional operator ( ? : ) are balanced to a common type • Balancing conversions involve two operands of different types, and one or both operands may be converted • After integer promotions are performed on both operands, the following rules are applied to the promoted operands. 1. If both operands have the same type, no further conversion is needed 2. If both operands are of the same integer type (signed or unsigned), the operand with the type of lesser integer conversion rank is converted to the type of the operand with greater rank. 23

3. If the operand that has unsigned integer type has rank greater than or equal to the rank of the type of the other operand, the operand with signed integer type is converted to the type of the operand with unsigned integer type. 4. If the type of the operand with signed integer type can represent all of the values of the type of the operand with unsigned integer type, the operand with unsigned integer type is converted to the type of the operand with signed integer type. Otherwise, both operands are converted to the unsigned integer type corresponding to the type of the operand with signed integer type. Specific operations can add to or modify the semantics of the usual arithmetic operations. 24

Apply Integer Promotions Rank(signed) > Rank(unsigned) Same type ? No additional conversion Yes No Both signed or both unsigned? Convert lesser rank to higher rank Rank(unsigned) >= Rank(signed) Convert signed integer type to the type of the operand with unsigned integer type Can signed type represent all values of unsigned type? Convert unsigned integer type to the type of the operand with signed integer type Convert both operands to the unsigned integer type corresponding to the type of the operand with signed integer type 25

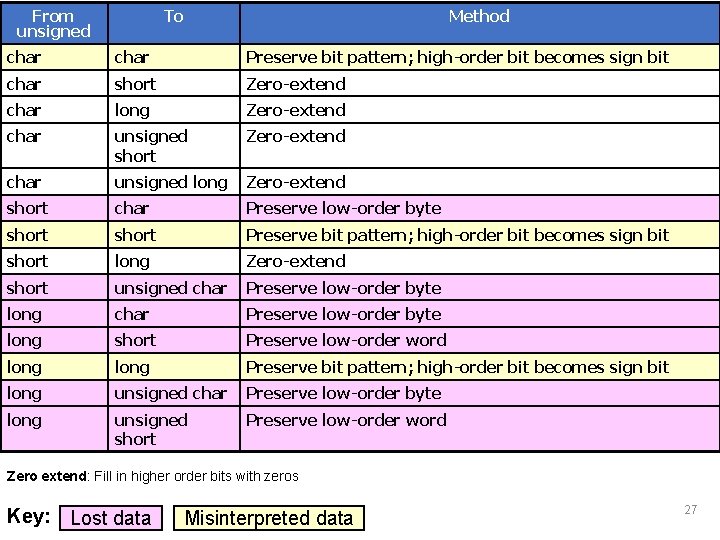
Unsigned Integer Conversions • Conversions of smaller unsigned integer types to larger unsigned integer types is • Always safe • Typically accomplished by zero-extending the value • When a larger unsigned integer is converted to a smaller unsigned integer type the • Larger value is truncated • Low-order bits are preserved • When unsigned integer types converted to the corresponding signed integer type • The bit pattern is preserved so no data is lost • The high-order bit becomes the sign bit • If the sign bit is set, both sign and magnitude of value changes. 26

From unsigned To Method char Preserve bit pattern; high-order bit becomes sign bit char short Zero-extend char long Zero-extend char unsigned short Zero-extend char unsigned long Zero-extend short char Preserve low-order byte short Preserve bit pattern; high-order bit becomes sign bit short long Zero-extend short unsigned char Preserve low-order byte long short Preserve low-order word long Preserve bit pattern; high-order bit becomes sign bit long unsigned char Preserve low-order byte long unsigned short Preserve low-order word Zero extend: Fill in higher order bits with zeros Key: Lost data Misinterpreted data 27

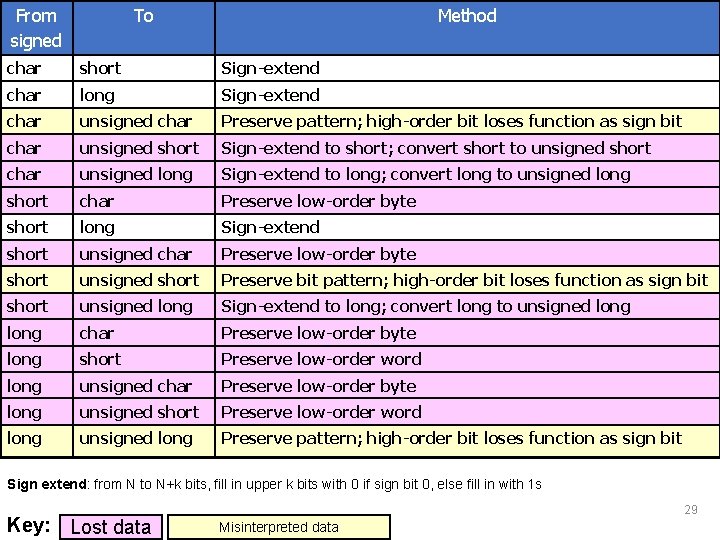
Signed Integer Conversions • A signed integer is converted to a shorter signed integer by truncating the high-order bits • When signed integer is converted to an unsigned integer of equal or greater size and value of the signed integer is not negative • The value is unchanged • The signed integer is sign-extended Sign extend from N to N+k bits: fill in upper k bits with 0 if sign bit 0, else fill in with 1 s • When signed integers are converted to unsigned integer • Bit pattern is preserved - no lost data • High-order bit loses its function as a sign bit • If the value of the signed integer is not negative, the value is unchanged • If the value is negative, the resulting unsigned value is evaluated as a large, signed integer. 28

From signed To Method char short Sign-extend char long Sign-extend char unsigned char Preserve pattern; high-order bit loses function as sign bit char unsigned short Sign-extend to short; convert short to unsigned short char unsigned long Sign-extend to long; convert long to unsigned long short char Preserve low-order byte short long Sign-extend short unsigned char Preserve low-order byte short unsigned short Preserve bit pattern; high-order bit loses function as sign bit short unsigned long Sign-extend to long; convert long to unsigned long char Preserve low-order byte long short Preserve low-order word long unsigned char Preserve low-order byte long unsigned short Preserve low-order word long unsigned long Preserve pattern; high-order bit loses function as sign bit Sign extend: from N to N+k bits, fill in upper k bits with 0 if sign bit 0, else fill in with 1 s Key: Lost data 29 Misinterpreted data

Example 1 main(){ int i; short int s; 0 x 80000000 + 0 x 00000001 = 0 x 80000001 i=INT_MIN+1; s=i; 0 x 80000001 -> 0 x 0001 printf("i is <%d> INT_MIN is <%d>n", i, INT_MIN); printf("s is <%hd> n", s); } jmayo$. /trunc. Int i is <-2147483647> INT_MIN is <-2147483648> s is <1> jmayo$ 30

Example 2 int main}() signed s; unsigned u; signed q; Same bit pattern as UINT_MAX-1 (even) s=-2; u=2; printf("s is <%d> u is <%u>n", s, u; ( q=s/u; Rank unsigned >= rank signed UINT_MAX = 4, 294, 967, 295 = 232 -1 s as unsigned is 4, 294, 967, 294=232 -2 s/2 is 2147483647 (= 231 -1 = INT_MAX) printf(”q is <%d>n", q; ( { jmayo$/. conv s is <-2> u is <2< q is <2147483647< 31

3) Integer Operations Will look at operations and identify exceptional conditions that can result in vulnerabilities Assignment • Right operand converted to type of left operand • Can result in truncation Addition • Addition can be used to add two arithmetic operands or a pointer and an integer. • If both operands are of arithmetic type, the usual arithmetic conversions are performed on them. • Signed addition can result in overflow • Unsigned addition can result in wraparound 32

Unsigned Integer Addition • Addition can result in wraparound if the sum of the lefthand side (LHS) and right-hand side (RHS) is greater than corresponding maximum (e. g. , UINT_MAX for unsigned int) • Precondition test (check for error before op performed) Overflow occurs when A and B are unsigned int and A + B > UINT_MAX Use #include <limits. h> unsigned int ui 1, ui 2, usum; if (ui 1 + ui 2 > UINT_MAX) if (UINT_MAX – ui 1 < ui 2) /* handle error */ else usum=ui 1+ui 2 Is this a valid check to see if operation will overflow? 33

• Postcondition test (perform operation and see if within limit) unsigned int ui 1, ui 2, usum; usum=ui 1+ui 2 if (usum < ui 1) /* handle error */ 34

Signed Integer Addition of signed integers is more complicated: LHS RHS Exception Condition Positive Overflow if INT_MAX – LHS < RHS Positive Negative None possible Negative Positive None possible Negative Overflow if LHS < INT_MIN – RHS Precondition: #include <limits. h> signed int si 1, si 2, ssum; if (((si 2 > 0) && (si 1 > (INT_MAX – si 2)) || ((si 2 < 0) && (si 1 < (INT_MIN – si 2)))) /* handle error */ else ssum=si 1+si 2 SEI CERT C Coding Standard: Rules fir Developing Safe, Reliable, and Secure Systems (2016 Edition) 35

Postcondition: Let sum = lhs + rhs. • If lhs is non-negative and sum < rhs, an overflow has occurred. • If lhs is negative and sum > rhs, an overflow has occurred. • In all other cases, the addition operation succeeds without overflow. 36

Upcast then Downcast • Sum of two integers of width w can always fit in an integer of width w+1 bits, • Can perform the addition in a type with greater width and then range check before downcasting to original type 37

Integer Subtraction diff=s 1 -s 2 • Signed • Overflow from subtraction on signed integers cannot occur when both operands are positive or both are negative. • Precondition: signed int si 1, si 2, sdiff; if ((s 2>0 && s 1 < INT_MIN + s 2)|| (s 2<0 && s 1 > INT_MAX + s 2)) /* handle error */ else sdiff=s 1 -s 2 The SEI CERT C Coding Standard: Rules for Developing Safe, Reliable, and Secure Systems. (2016 Edition) 38

• Unsigned • Wraparound occurs if difference between the operands is negative • Precondition unsigned int ui 1, ui 2, udiff; if (ui 1 < ui 2) /* handle error */ else udiff=ui 1 -ui 2 • Postcondition: unsigned int ui 1, ui 2, udiff; udiff=ui 1 -ui 2; if (udiff > ui 1) /* handle error */ The SEI CERT C Coding Standard: Rules for Developing Safe, Reliable, and Secure Systems. (2016 Edition) 39

Integer Multiplication • Multiplication is prone to overflow errors because relatively small operands can overflow • Product of two integer operands can always be represented using twice the number of bits of the larger of the two operands. • Upcast can avoid overflow. • Must ensure result can be represented in destination type before downcasting 40

• Signed precondition: si 1 si 2 Error when positive si 1 > (INT_MAX/si 2) positive non-positive si 2 < (INT_MIN/si 1) non-positive si 1 < (INT_MIN/si 2) non-positive (si 1!=0) && (si 2 < (INT_MAX/si 1)) If no error, multiplication OK. • Unsigned precondition: unsigned int ui 1, ui 2, product; if (ui 1>UINT_MAX/ui 2) /* handle error */ else product=ui 1*ui 2 Secure Coding in C and C++, Second Edition, Robert Seacord 41

• Signed downcast (int to twice number of bits; op; downcast w/check) static_assert( sizeof(long) > 2*sizeof(int), “Unable to detect overflow after multiplication” ); long tmp=(long)si 1 * (long)si 2; if ( (tmp > INT_MAX) || (tmp < INT_MIN)) /* handle overflow*/ else product = (int)tmp; • Unsigned downcast static_assert( sizeof(unsigned long) > 2*sizeof(unsigned int), “Unable to detect wrapping after multiplication” ); unsigned long tmp=(unsigned long)si 1 * (unsigned long)si 2; if (tmp > UINT_MAX) /* handle wrapping */ else product = (unsigned int)tmp; 42

Upcast Example void* Alloc. Blocks(size_t c. Blocks) { // allocating no blocks is an error if (c. Blocks == 0) return NULL; // Allocate enough memory // Upcast the result to a 64 -bit integer // and check against 32 -bit UINT_MAX // to makes sure there's no overflow ULONG alloc = c. Blocks * 16; return (alloc < UINT_MAX) ? malloc(c. Blocks * 16): NULL; } Can you find the error? This is a 32 -bit operation that results in a 32 -bit value. The result is assigned to a ULONG but the calculation may have already overflowed. 43

Corrected Upcast Example void* Alloc. Blocks(size_t c. Blocks) { // allocating no blocks is an error if (c. Blocks == 0) return NULL; // Allocate enough memory // Upcast the result to a 64 -bit integer // and check against 32 -bit UINT_MAX // to makes sure there's no overflow ULONG alloc = (ULONG)c. Blocks*16; return (alloc < UINT_MAX) ? malloc(c. Blocks * 16) : NULL; } 44

Integer Division • Behavior of / and % undefined if second operator is zero • Unsigned integer division cannot wrap • Signed overflow may occur when minimum two’s complement value is divided by -1 • Signed precondition (for longs) signed long sl 1, sl 2, quotient, result; if ( (sl 2==0) || ((sl 1==LONG_MIN)&&(sl 2==-1))) /* handle error */ else quotient=sl 1/sl 2; /* or result = sl 1%sl 2 for remainder */ 45

Review • Improper use of integers emerging target of attacks • Conversions, arithmetic operations may cause unanticipated values • Conversions: • Determine width/representation of result of mixed type operands • Integer promotions • Usual arithmetic conversions • Result of conversion • Larger -> smaller: truncation, preserve bit pattern, signedness determines value • Signed <-> unsigned: preserve bit pattern, signedness determines value • Smaller->larger: zero-extend (unsigned to any) or sign-extend (signed to any) • Result of arithmetic operations • Range check 46