C Plus Data Structures Nell Dale David Teague

C++ Plus Data Structures Nell Dale David Teague Chapter 5 Linked Structures Slides by Sylvia Sorkin, Community College of Baltimore County - Essex Campus 1

Definition of Stack • Logical (or ADT) level: A stack is an ordered group of homogeneous items (elements), in which the removal and addition of stack items can take place only at the top of the stack. • A stack is a LIFO “last in, first out” structure. 2

Stack ADT Operations • Make. Empty -- Sets stack to an empty state. • Is. Empty -- Determines whether the stack is currently empty. • Is. Full -- Determines whether the stack is currently full. • Push (Item. Type new. Item) -- Adds new. Item to the top of the stack. • Pop (Item. Type& item) -- Removes the item at the top of the stack and returns it in item. 3

ADT Stack Operations Transformers • Make. Empty • Push • Pop change state Observers • Is. Empty observe state • Is. Full 4

Another Stack Implementation • One advantage of an ADT is that the kind of implementation used can be changed. • The dynamic array implementation of the stack has a weakness -- the maximum size of the stack is passed to the constructor as parameter. • Instead we can dynamically allocate the space for each stack element as it is pushed onto the stack. 5

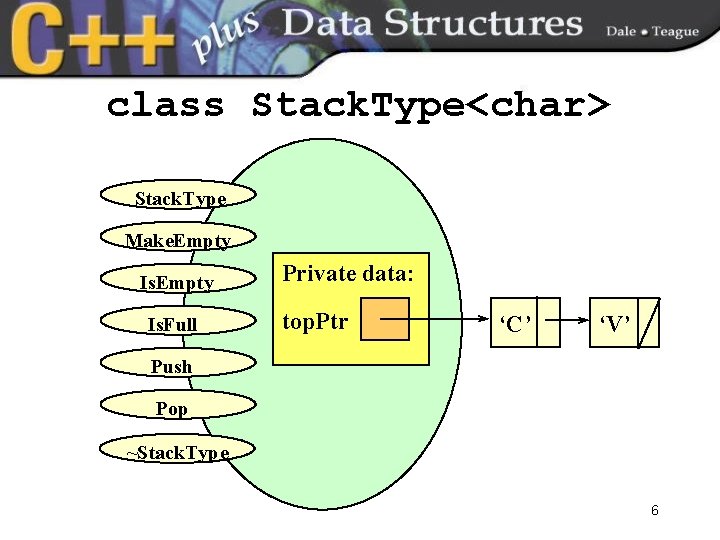
class Stack. Type<char> Stack. Type Make. Empty Is. Full Private data: top. Ptr ‘C’ ‘V’ Push Pop ~Stack. Type 6

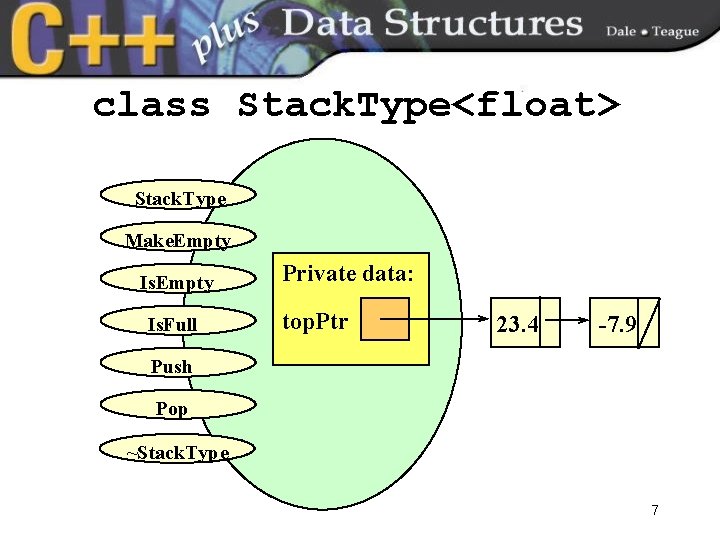
class Stack. Type<float> Stack. Type Make. Empty Is. Full Private data: top. Ptr 23. 4 -7. 9 Push Pop ~Stack. Type 7

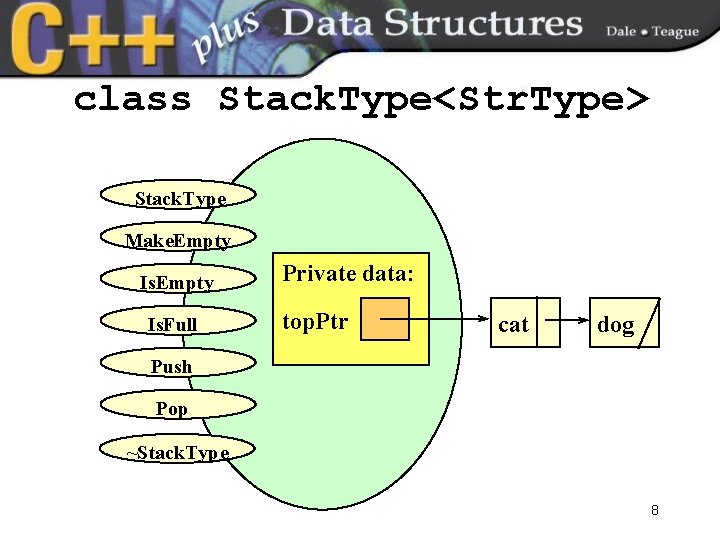
class Stack. Type<Str. Type> Stack. Type Make. Empty Is. Full Private data: top. Ptr cat dog Push Pop ~Stack. Type 8

letter char ‘V’ Tracing Client Code letter = ‘V’; Stack. Type< char > my. Stack; my. Stack. Push(letter); my. Stack. Push(‘C’); my. Stack. Push(‘S’); if ( !my. Stack. Is. Empty( ) ) my. Stack. Pop( letter ); my. Stack. Push(‘K’); 9

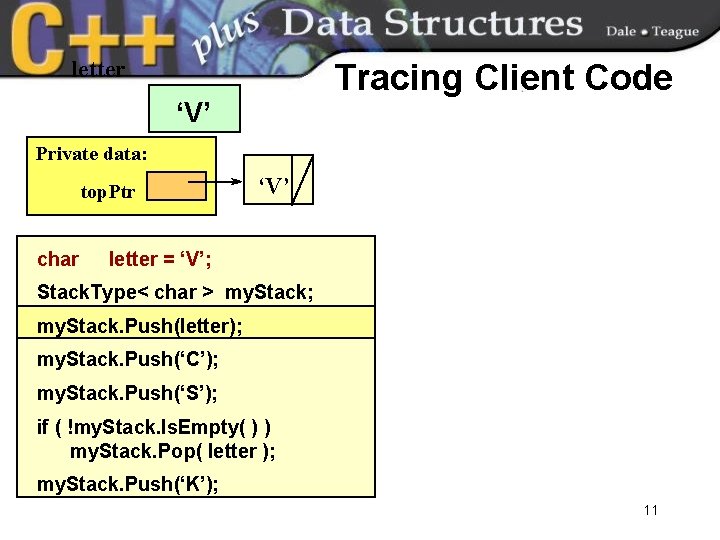
letter ‘V’ Tracing Client Code Private data: top. Ptr NULL char letter = ‘V’; Stack. Type< char > my. Stack; my. Stack. Push(letter); my. Stack. Push(‘C’); my. Stack. Push(‘S’); if ( !my. Stack. Is. Empty( ) ) my. Stack. Pop( letter ); my. Stack. Push(‘K’); 10

letter Tracing Client Code ‘V’ Private data: top. Ptr char ‘V’ letter = ‘V’; Stack. Type< char > my. Stack; my. Stack. Push(letter); my. Stack. Push(‘C’); my. Stack. Push(‘S’); if ( !my. Stack. Is. Empty( ) ) my. Stack. Pop( letter ); my. Stack. Push(‘K’); 11

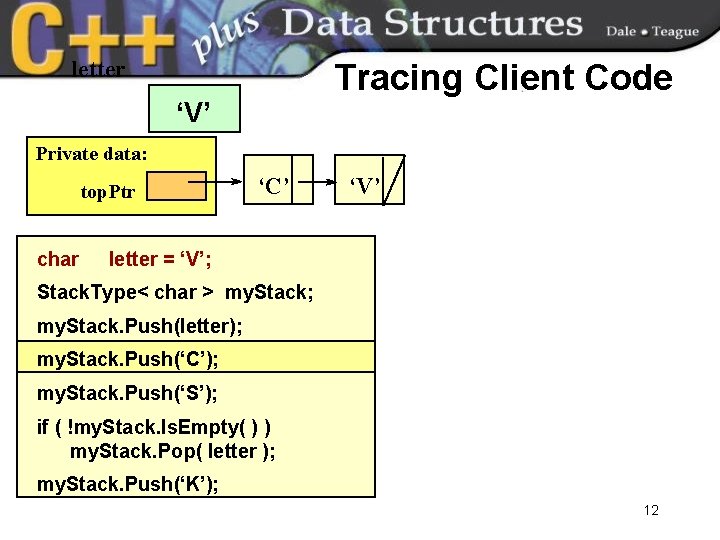
letter Tracing Client Code ‘V’ Private data: top. Ptr char ‘C’ ‘V’ letter = ‘V’; Stack. Type< char > my. Stack; my. Stack. Push(letter); my. Stack. Push(‘C’); my. Stack. Push(‘S’); if ( !my. Stack. Is. Empty( ) ) my. Stack. Pop( letter ); my. Stack. Push(‘K’); 12

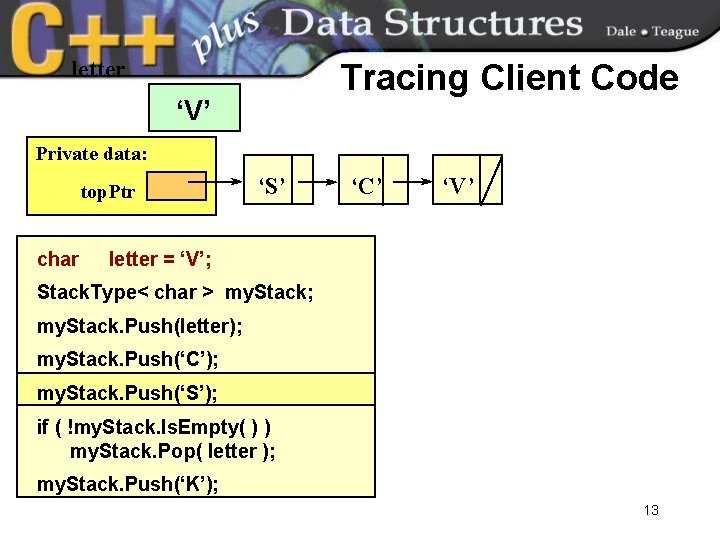
letter Tracing Client Code ‘V’ Private data: top. Ptr char ‘S’ ‘C’ ‘V’ letter = ‘V’; Stack. Type< char > my. Stack; my. Stack. Push(letter); my. Stack. Push(‘C’); my. Stack. Push(‘S’); if ( !my. Stack. Is. Empty( ) ) my. Stack. Pop( letter ); my. Stack. Push(‘K’); 13

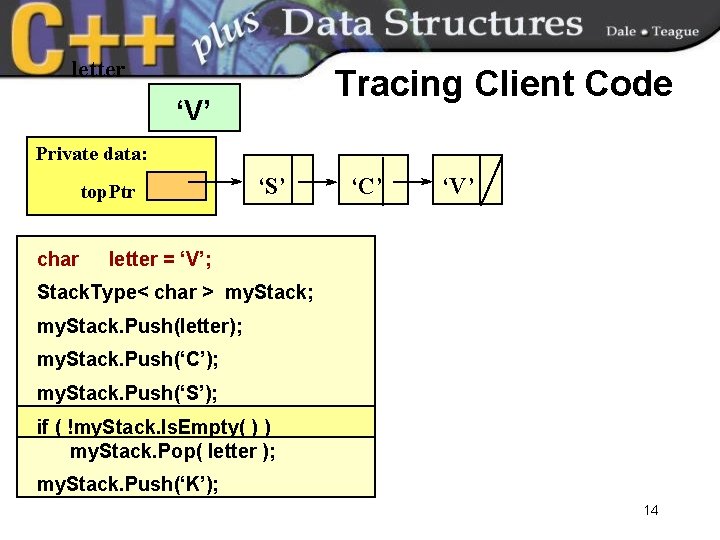
letter Tracing Client Code ‘V’ Private data: top. Ptr char ‘S’ ‘C’ ‘V’ letter = ‘V’; Stack. Type< char > my. Stack; my. Stack. Push(letter); my. Stack. Push(‘C’); my. Stack. Push(‘S’); if ( !my. Stack. Is. Empty( ) ) my. Stack. Pop( letter ); my. Stack. Push(‘K’); 14

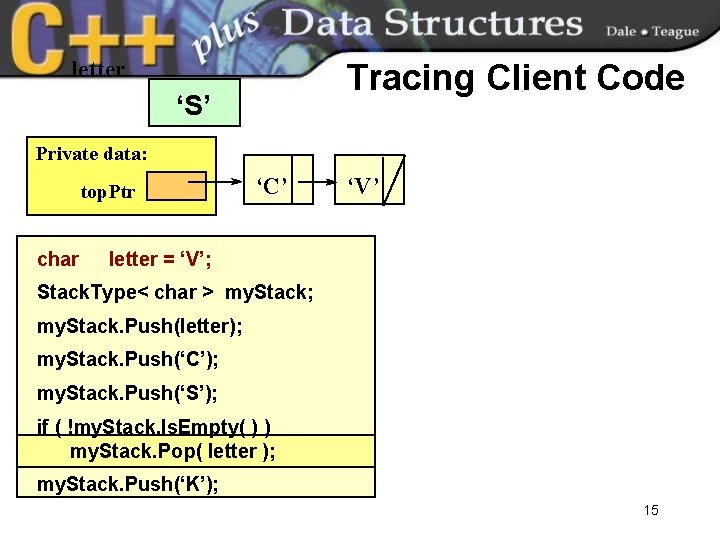
letter Tracing Client Code ‘S’ Private data: top. Ptr char ‘C’ ‘V’ letter = ‘V’; Stack. Type< char > my. Stack; my. Stack. Push(letter); my. Stack. Push(‘C’); my. Stack. Push(‘S’); if ( !my. Stack. Is. Empty( ) ) my. Stack. Pop( letter ); my. Stack. Push(‘K’); 15

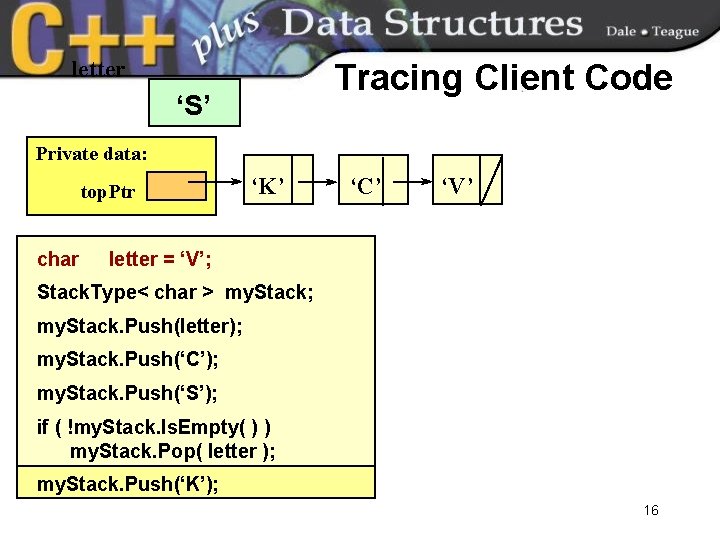
letter Tracing Client Code ‘S’ Private data: top. Ptr char ‘K’ ‘C’ ‘V’ letter = ‘V’; Stack. Type< char > my. Stack; my. Stack. Push(letter); my. Stack. Push(‘C’); my. Stack. Push(‘S’); if ( !my. Stack. Is. Empty( ) ) my. Stack. Pop( letter ); my. Stack. Push(‘K’); 16

Dynamically Linked Implementation of Stack // DYNAMICALLY LINKED IMPLEMENTATION OF STACK #include "Item. Type. h" // for Item. Type template<class Item. Type> struct Node. Type { Item. Type info; Node. Type<Item. Type>* next; } ‘A’ 6000 . info . next 17

// DYNAMICALLY LINKED IMPLEMENTATION OF STACK continued template<class Item. Type> class Stack. Type { public: Stack. Type( ); // constructor // Default constructor. // POST: Stack is created and empty. void Make. Empty( ); // PRE: None. // POST: Stack is empty. bool Is. Empty( ) const; // PRE: Stack has been initialized. // POST: Function value = (stack is empty) bool Is. Full( ) const; // PRE: Stack has been initialized. // POST: Function value = (stack is full) 18

// DYNAMICALLY LINKED IMPLEMENTATION OF STACK continued void Push( Item. Type item ); // PRE: Stack has been initialized. // Stack is not full. // POST: new. Item is at the top of the stack. void Pop( Item. Type& item ); // PRE: Stack has been initialized. // Stack is not empty. // POST: Top element has been removed from stack. // item is a copy of removed element. ~Stack. Type( ); // destructor // PRE: Stack has been initialized. // POST: Memory allocated for nodes has been // deallocated. private: Node. Type<Item. Type>* }; top. Ptr ; 19

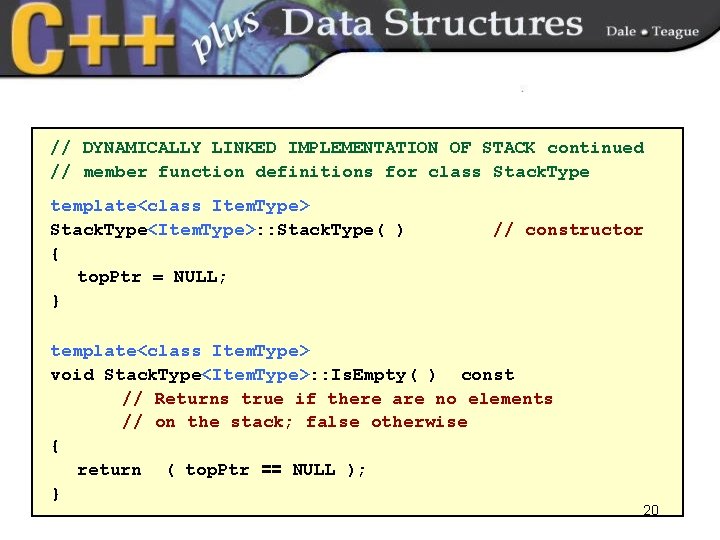
// DYNAMICALLY LINKED IMPLEMENTATION OF STACK continued // member function definitions for class Stack. Type template<class Item. Type> Stack. Type<Item. Type>: : Stack. Type( ) { top. Ptr = NULL; } // constructor template<class Item. Type> void Stack. Type<Item. Type>: : Is. Empty( ) const // Returns true if there are no elements // on the stack; false otherwise { return ( top. Ptr == NULL ); } 20

Using operator new If memory is available in an area called the free store (or heap), operator new allocates the requested object, and returns a pointer to the memory allocated. The dynamically allocated object exists until the delete operator destroys it. 21

new. Item ‘B’ Adding new. Item to the stack new. Item = ‘B’; Node. Type<char>* location; location = new Node. Type<char>; location->info = new. Item; location->next = top. Ptr; top. Ptr = location; top. Ptr ‘X’ ‘C’ ‘L’ 22

new. Item ‘B’ Adding new. Item to the stack new. Item = ‘B’; Node. Type<char>* location; location = new Node. Type<char>; location->info = new. Item; location->next = top. Ptr; top. Ptr = location; top. Ptr ‘X’ ‘C’ ‘L’ location 23

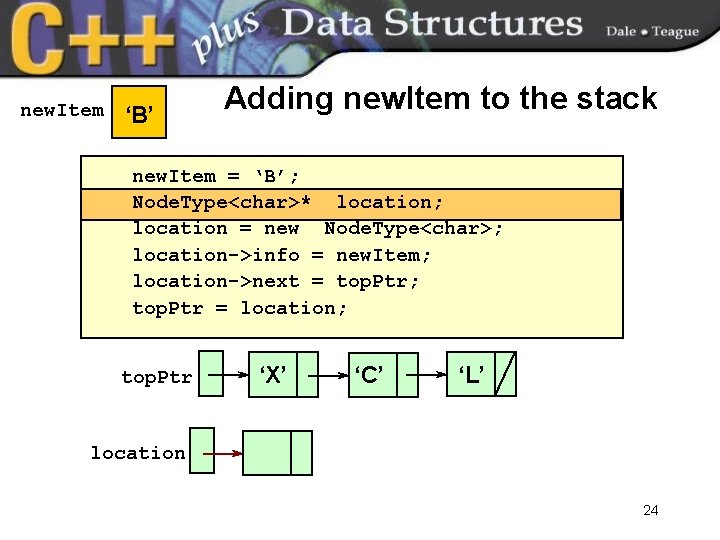
new. Item ‘B’ Adding new. Item to the stack new. Item = ‘B’; Node. Type<char>* location; location = new Node. Type<char>; location->info = new. Item; location->next = top. Ptr; top. Ptr = location; top. Ptr ‘X’ ‘C’ ‘L’ location 24

new. Item ‘B’ Adding new. Item to the stack new. Item = ‘B’; Node. Type<char>* location; location = new Node. Type<char>; location->info = new. Item; location->next = top. Ptr; top. Ptr = location; top. Ptr location ‘X’ ‘C’ ‘L’ ‘B’ 25

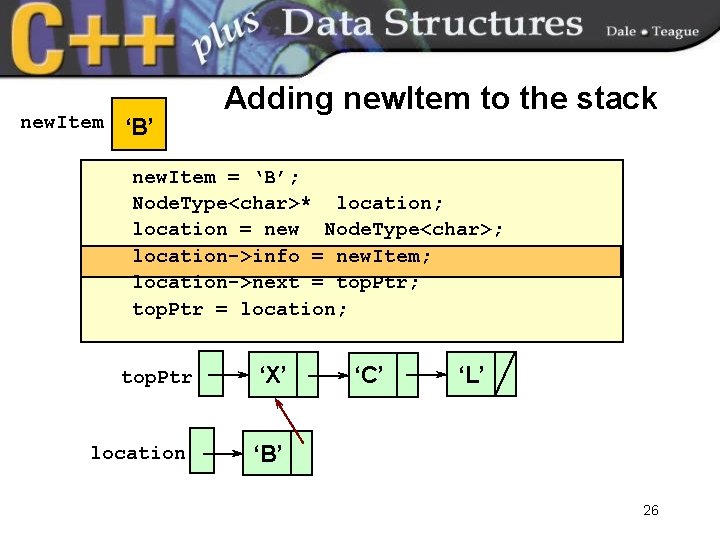
new. Item ‘B’ Adding new. Item to the stack new. Item = ‘B’; Node. Type<char>* location; location = new Node. Type<char>; location->info = new. Item; location->next = top. Ptr; top. Ptr = location; top. Ptr location ‘X’ ‘C’ ‘L’ ‘B’ 26

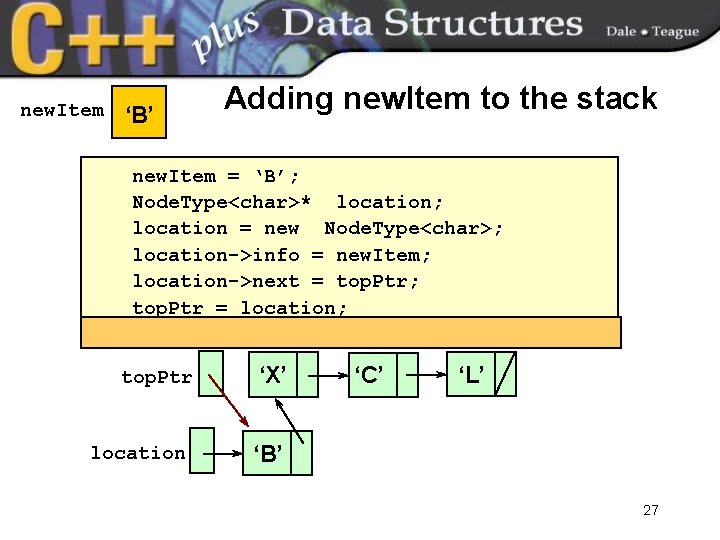
new. Item ‘B’ Adding new. Item to the stack new. Item = ‘B’; Node. Type<char>* location; location = new Node. Type<char>; location->info = new. Item; location->next = top. Ptr; top. Ptr = location; top. Ptr location ‘X’ ‘C’ ‘L’ ‘B’ 27

Implementing Push template<class Item. Type> void Stack. Type<Item. Type>: : Push ( Item. Type new. Item ) // Adds new. Item to the top of the stack. { if (Is. Full()) throw Push. On. Full. Stack(); Node. Type<Item. Type>* location; location = new Node. Type<Item. Type>; location->info = new. Item; location->next = top. Ptr; top. Ptr = location; } 28

Using operator delete The object currently pointed to by the pointer is deallocated, and the pointer is considered unassigned. The memory is returned to the free store. 29

Deleting item from the stack Node. Type<Item. Type>* temp. Ptr; item = top. Ptr->info; temp. Ptr = top. Ptr; top. Ptr = top. Ptr->next; delete temp. Ptr; top. Ptr ‘B’ ‘X’ ‘C’ ‘L’ temp. Ptr 30

item ‘B’ Deleting item from the stack Node. Type<Item. Type>* temp. Ptr; item = top. Ptr->info; temp. Ptr = top. Ptr; top. Ptr = top. Ptr->next; delete temp. Ptr; top. Ptr ‘B’ ‘X’ ‘C’ ‘L’ temp. Ptr 31

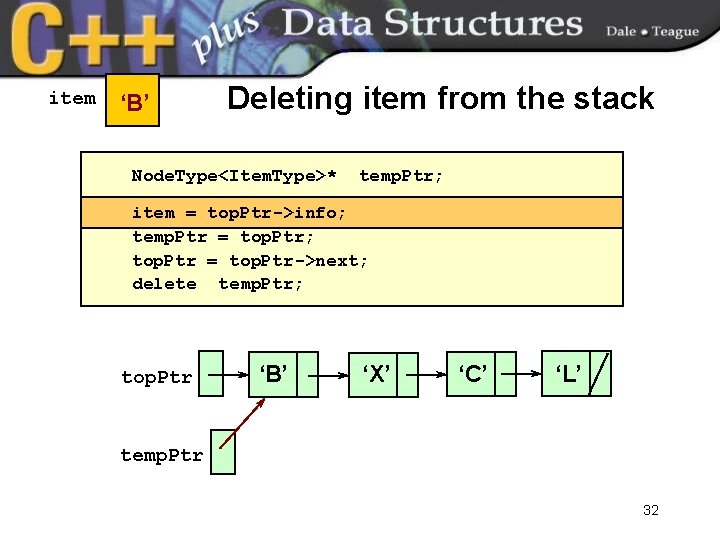
item ‘B’ Deleting item from the stack Node. Type<Item. Type>* temp. Ptr; item = top. Ptr->info; temp. Ptr = top. Ptr; top. Ptr = top. Ptr->next; delete temp. Ptr; top. Ptr ‘B’ ‘X’ ‘C’ ‘L’ temp. Ptr 32

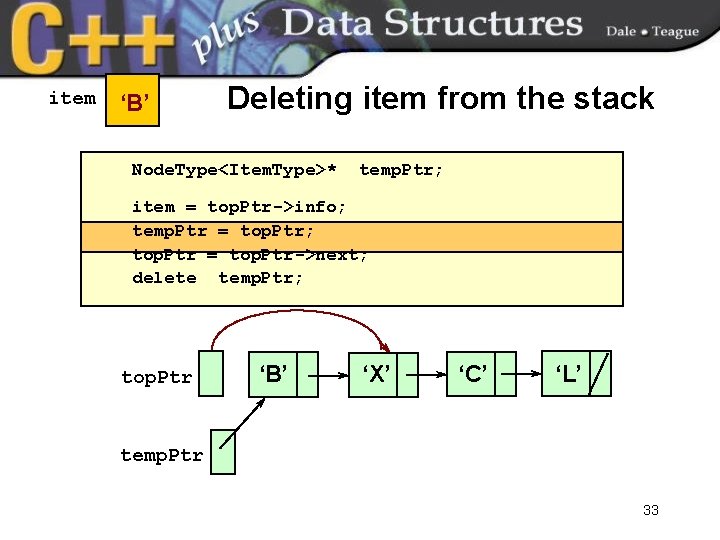
item ‘B’ Deleting item from the stack Node. Type<Item. Type>* temp. Ptr; item = top. Ptr->info; temp. Ptr = top. Ptr; top. Ptr = top. Ptr->next; delete temp. Ptr; top. Ptr ‘B’ ‘X’ ‘C’ ‘L’ temp. Ptr 33

item ‘B’ Deleting item from the stack Node. Type<Item. Type>* temp. Ptr; item = top. Ptr->info; temp. Ptr = top. Ptr; top. Ptr = top. Ptr->next; delete temp. Ptr; top. Ptr ‘X’ ‘C’ ‘L’ temp. Ptr 34

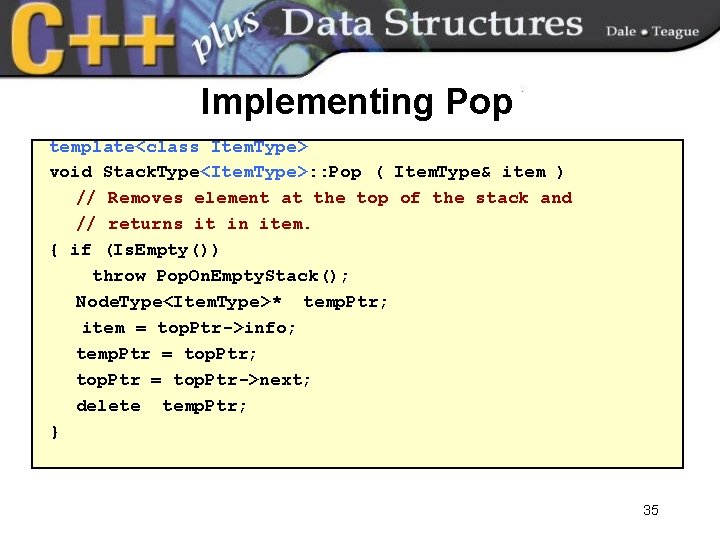
Implementing Pop template<class Item. Type> void Stack. Type<Item. Type>: : Pop ( Item. Type& item ) // Removes element at the top of the stack and // returns it in item. { if (Is. Empty()) throw Pop. On. Empty. Stack(); Node. Type<Item. Type>* temp. Ptr; item = top. Ptr->info; temp. Ptr = top. Ptr; top. Ptr = top. Ptr->next; delete temp. Ptr; } 35

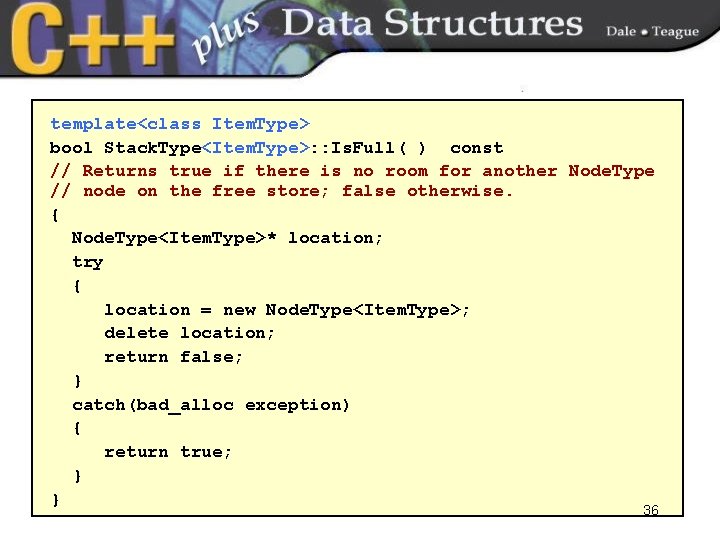
template<class Item. Type> bool Stack. Type<Item. Type>: : Is. Full( ) const // Returns true if there is no room for another Node. Type // node on the free store; false otherwise. { Node. Type<Item. Type>* location; try { location = new Node. Type<Item. Type>; delete location; return false; } catch(bad_alloc exception) { return true; } } 36

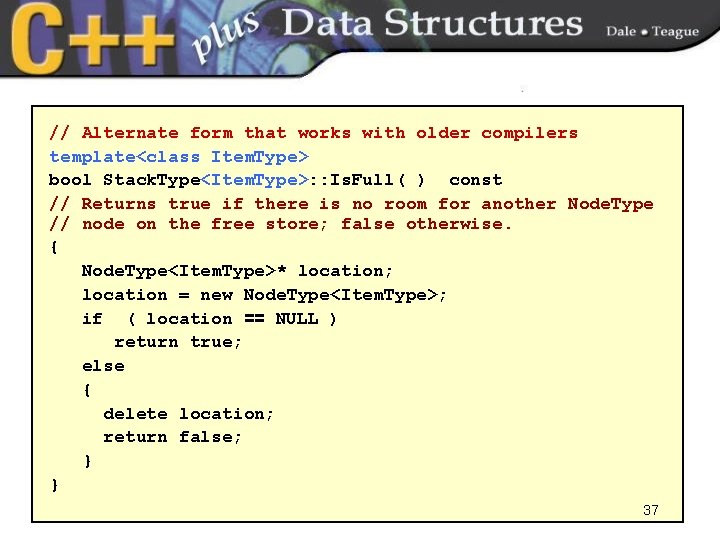
// Alternate form that works with older compilers template<class Item. Type> bool Stack. Type<Item. Type>: : Is. Full( ) const // Returns true if there is no room for another Node. Type // node on the free store; false otherwise. { Node. Type<Item. Type>* location; location = new Node. Type<Item. Type>; if ( location == NULL ) return true; else { delete location; return false; } } 37

Why is a destructor needed? When a local stack variable goes out of scope, the memory space for data member top. Ptr is deallocated. But the nodes that top. Ptr points to are not automatically deallocated. A class destructor is used to deallocate the dynamic memory pointed to by the data member. 38

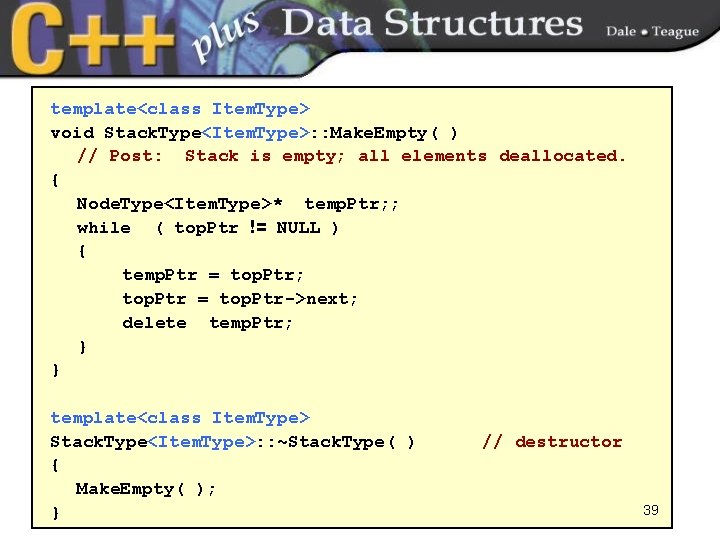
template<class Item. Type> void Stack. Type<Item. Type>: : Make. Empty( ) // Post: Stack is empty; all elements deallocated. { Node. Type<Item. Type>* temp. Ptr; ; while ( top. Ptr != NULL ) { temp. Ptr = top. Ptr; top. Ptr = top. Ptr->next; delete temp. Ptr; } } template<class Item. Type> Stack. Type<Item. Type>: : ~Stack. Type( ) { Make. Empty( ); } // destructor 39

What is a Queue? • Logical (or ADT) level: A queue is an ordered group of homogeneous items (elements), in which new elements are added at one end (the rear), and elements are removed from the other end (the front). • A queue is a FIFO “first in, first out” structure. 40

Queue ADT Operations • Make. Empty -- Sets queue to an empty state. • Is. Empty -- Determines whether the queue is currently empty. • Is. Full -- Determines whether the queue is currently full. • Enqueue (Item. Type new. Item) -- Adds new. Item to the rear of the queue. • Dequeue (Item. Type& item) -- Removes the item at the front of the queue and returns it in item. 41

ADT Queue Operations Transformers • Make. Empty • Enqueue • Dequeue change state Observers • Is. Empty observe state • Is. Full 42

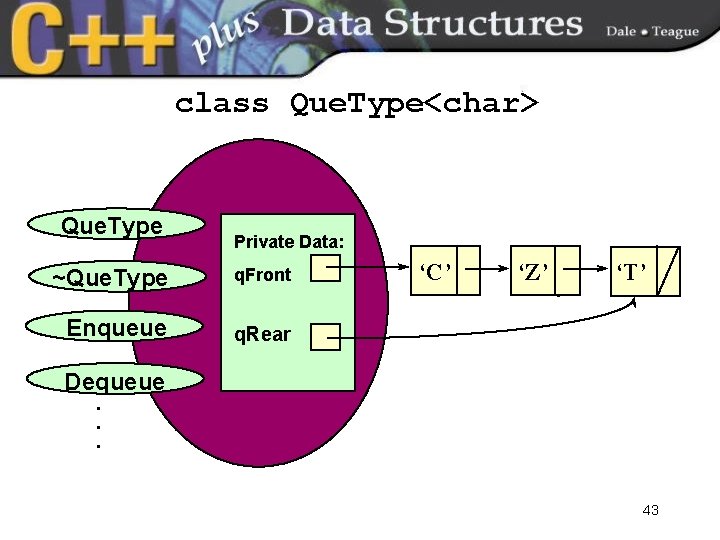
class Que. Type<char> Que. Type Private Data: ~Que. Type q. Front Enqueue q. Rear ‘C’ ‘Z’ ‘T’ Dequeue. . . 43

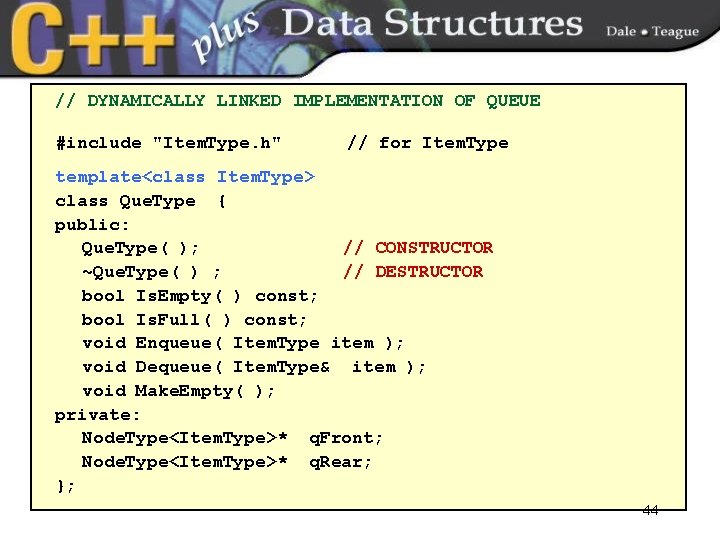
// DYNAMICALLY LINKED IMPLEMENTATION OF QUEUE #include "Item. Type. h" // for Item. Type template<class Item. Type> class Que. Type { public: Que. Type( ); // CONSTRUCTOR ~Que. Type( ) ; // DESTRUCTOR bool Is. Empty( ) const; bool Is. Full( ) const; void Enqueue( Item. Type item ); void Dequeue( Item. Type& item ); void Make. Empty( ); private: Node. Type<Item. Type>* q. Front; Node. Type<Item. Type>* q. Rear; }; 44

// DYNAMICALLY LINKED IMPLEMENTATION OF QUEUE continued // member function definitions for class Que. Type template<class Item. Type> Que. Type<Item. Type>: : Que. Type( ) { q. Front = NULL; q. Rear = NULL; } // CONSTRUCTOR template<class Item. Type> bool Que. Type<Item. Type>: : Is. Empty( ) const { return ( q. Front == NULL ) } 45

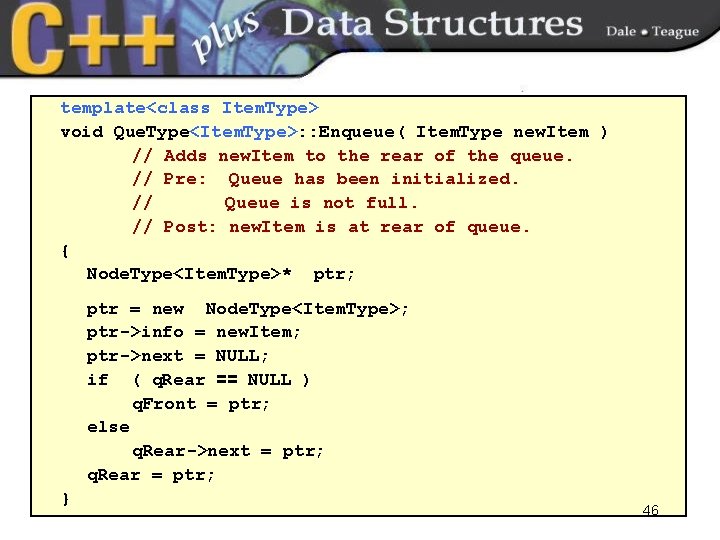
template<class Item. Type> void Que. Type<Item. Type>: : Enqueue( Item. Type new. Item ) // Adds new. Item to the rear of the queue. // Pre: Queue has been initialized. // Queue is not full. // Post: new. Item is at rear of queue. { Node. Type<Item. Type>* ptr; ptr = new Node. Type<Item. Type>; ptr->info = new. Item; ptr->next = NULL; if ( q. Rear == NULL ) q. Front = ptr; else q. Rear->next = ptr; q. Rear = ptr; } 46

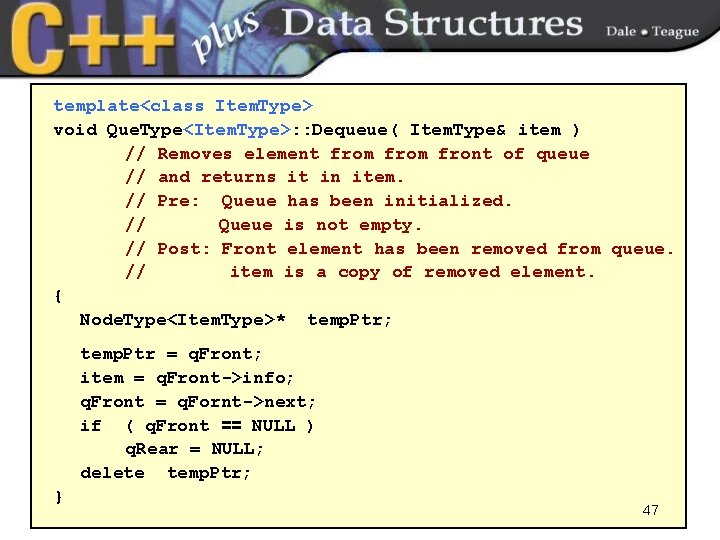
template<class Item. Type> void Que. Type<Item. Type>: : Dequeue( Item. Type& item ) // Removes element from front of queue // and returns it in item. // Pre: Queue has been initialized. // Queue is not empty. // Post: Front element has been removed from queue. // item is a copy of removed element. { Node. Type<Item. Type>* temp. Ptr; temp. Ptr = q. Front; item = q. Front->info; q. Front = q. Fornt->next; if ( q. Front == NULL ) q. Rear = NULL; delete temp. Ptr; } 47

What is a List? • A list is a homogeneous collection of elements, with a linear relationship between elements. • That is, each list element (except the first) has a unique predecessor, and each element (except the last) has a unique successor. 48

ADT Unsorted List Operations Transformers • Make. Empty • Insert. Item • Delete. Item change state Observers • Is. Full • Length. Is • Retrieve. Item observe state Iterators • Reset. List • Get. Next. Item process all 49

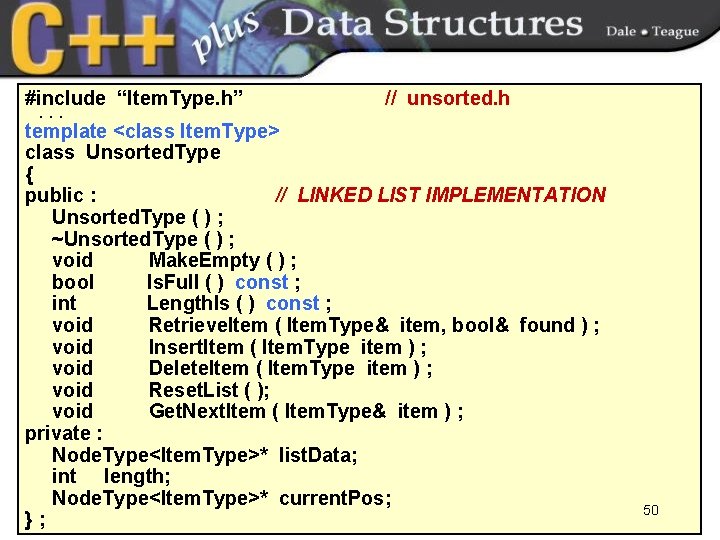
#include “Item. Type. h”. . . // unsorted. h template <class Item. Type> class Unsorted. Type { public : // LINKED LIST IMPLEMENTATION Unsorted. Type ( ) ; ~Unsorted. Type ( ) ; void Make. Empty ( ) ; bool Is. Full ( ) const ; int Length. Is ( ) const ; void Retrieve. Item ( Item. Type& item, bool& found ) ; void Insert. Item ( Item. Type item ) ; void Delete. Item ( Item. Type item ) ; void Reset. List ( ); void Get. Next. Item ( Item. Type& item ) ; private : Node. Type<Item. Type>* list. Data; int length; Node. Type<Item. Type>* current. Pos; }; 50

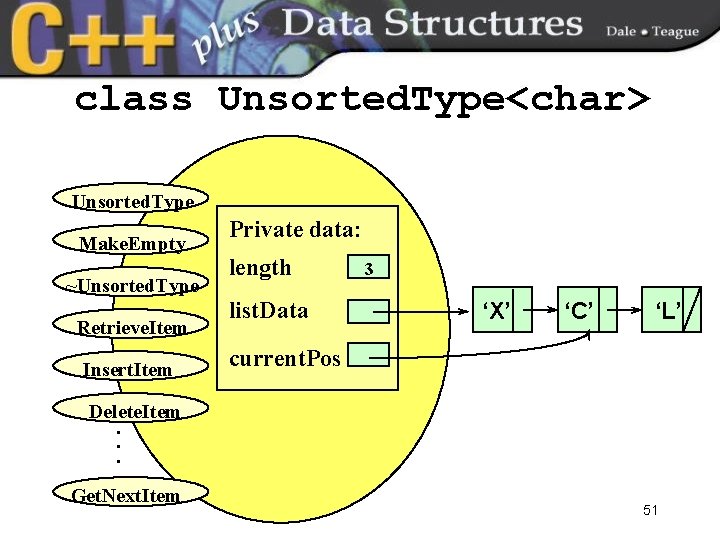
class Unsorted. Type<char> Unsorted. Type Make. Empty ~Unsorted. Type Retrieve. Item Insert. Item Private data: length list. Data 3 ‘X’ ‘C’ ‘L’ current. Pos Delete. Item. . . Get. Next. Item 51

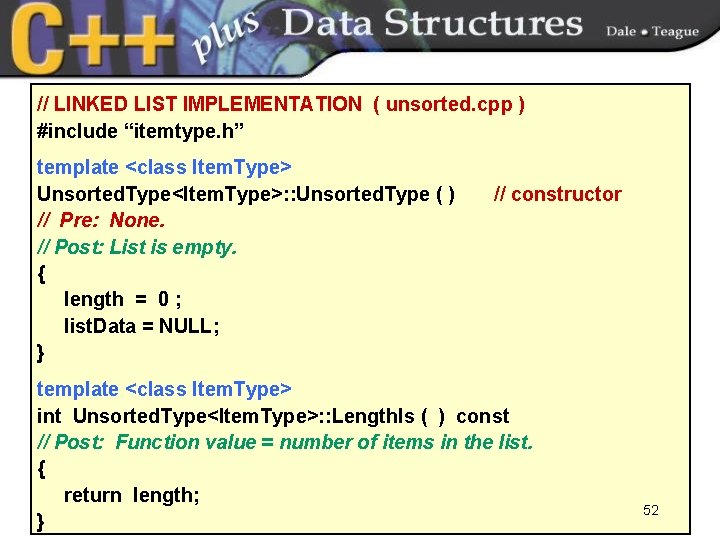
// LINKED LIST IMPLEMENTATION ( unsorted. cpp ) #include “itemtype. h” template <class Item. Type> Unsorted. Type<Item. Type>: : Unsorted. Type ( ) // Pre: None. // Post: List is empty. { length = 0 ; list. Data = NULL; } // constructor template <class Item. Type> int Unsorted. Type<Item. Type>: : Length. Is ( ) const // Post: Function value = number of items in the list. { return length; } 52

template <class Item. Type> void Unsorted. Type<Item. Type>: : Retrieve. Item( Item. Type& item, bool& found ) // Pre: Key member of item is initialized. // Post: If found, item’s key matches an element’s key in the list and a copy // of that element has been stored in item; otherwise, item is unchanged. { bool more. To. Search ; Node. Type<Item. Type>* location ; location = list. Data ; found = false ; more. To. Search = ( location != NULL ) ; while ( more. To. Search && !found ) { if ( item == location->info ) // match here { found = true ; item = location->info ; } else // advance pointer { location = location->next ; more. To. Search = ( location != NULL ) ; } } } 53

template <class Item. Type> void Unsorted. Type<Item. Type>: : Insert. Item ( Item. Type item ) // Pre: list is not full and item is not in list. // Post: item is in the list; length has been incremented. { Node. Type<Item. Type>* location ; // obtain and fill a node location = new Node. Type<Item. Type> ; location->info = item ; location->next = list. Data ; list. Data = location ; length++ ; } 54

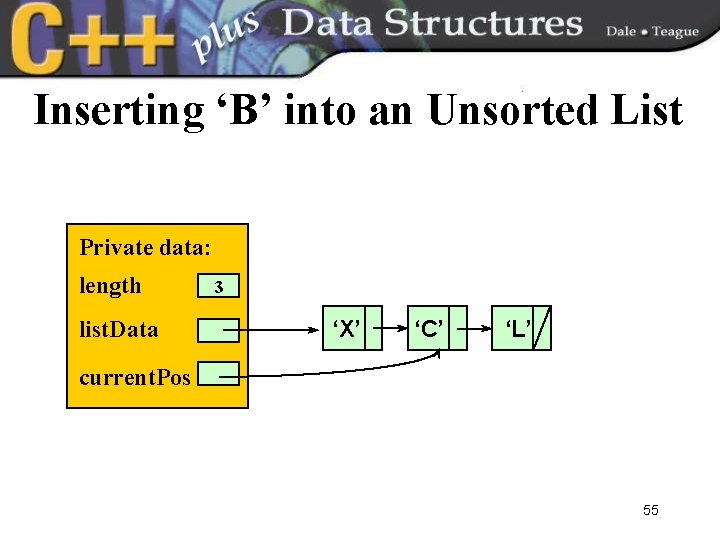
Inserting ‘B’ into an Unsorted List Private data: length list. Data 3 ‘X’ ‘C’ ‘L’ current. Pos 55

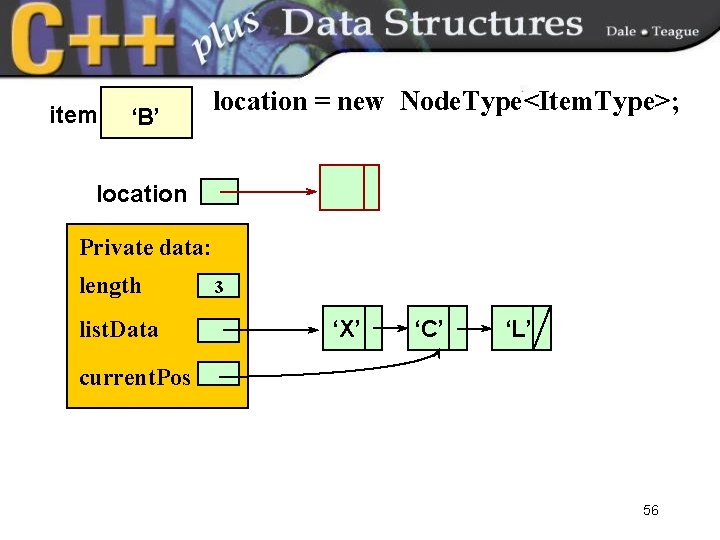
item ‘B’ location = new Node. Type<Item. Type>; location Private data: length list. Data 3 ‘X’ ‘C’ ‘L’ current. Pos 56

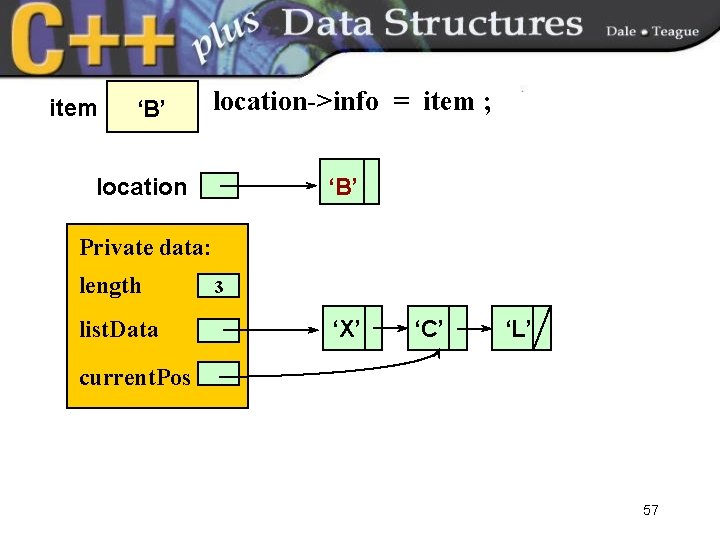
item ‘B’ location->info = item ; ‘B’ location Private data: length list. Data 3 ‘X’ ‘C’ ‘L’ current. Pos 57

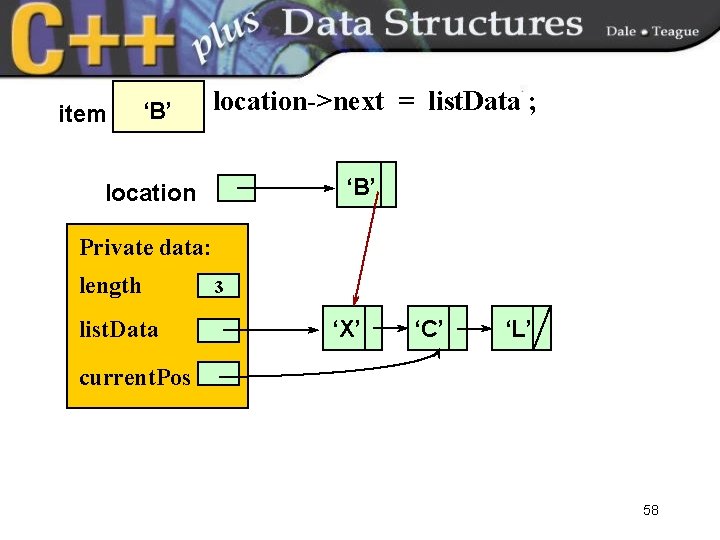
item ‘B’ location->next = list. Data ; ‘B’ location Private data: length list. Data 3 ‘X’ ‘C’ ‘L’ current. Pos 58

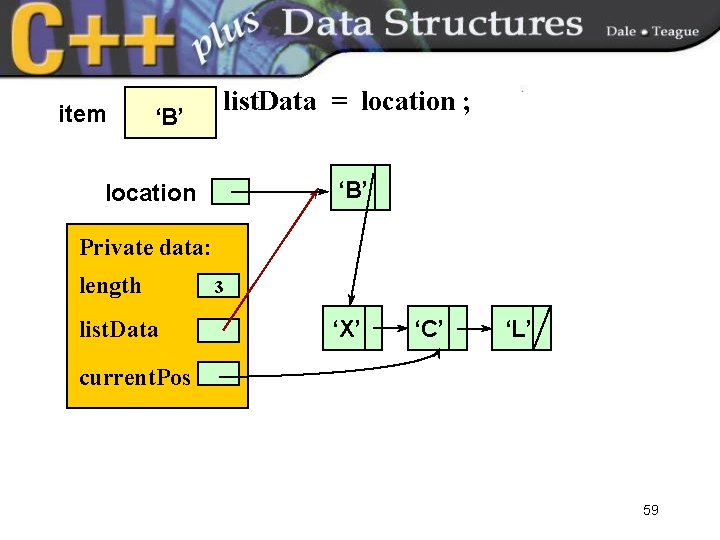
item ‘B’ list. Data = location ; ‘B’ location Private data: length list. Data 3 ‘X’ ‘C’ ‘L’ current. Pos 59

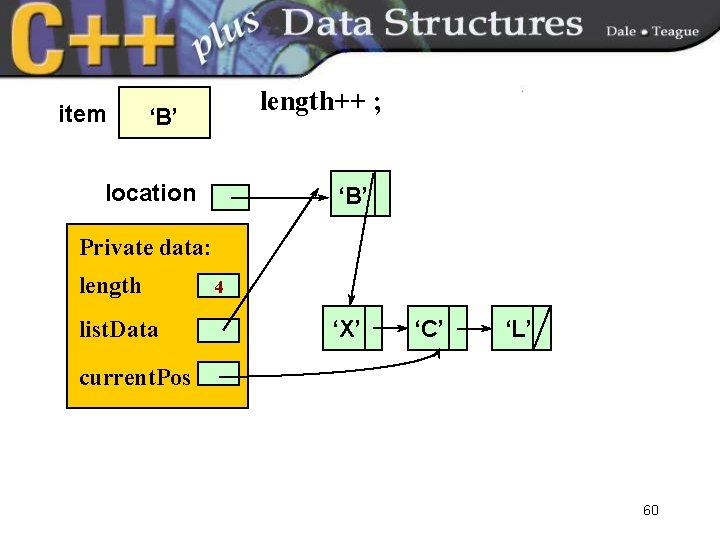
item length++ ; ‘B’ location ‘B’ Private data: length list. Data 4 ‘X’ ‘C’ ‘L’ current. Pos 60

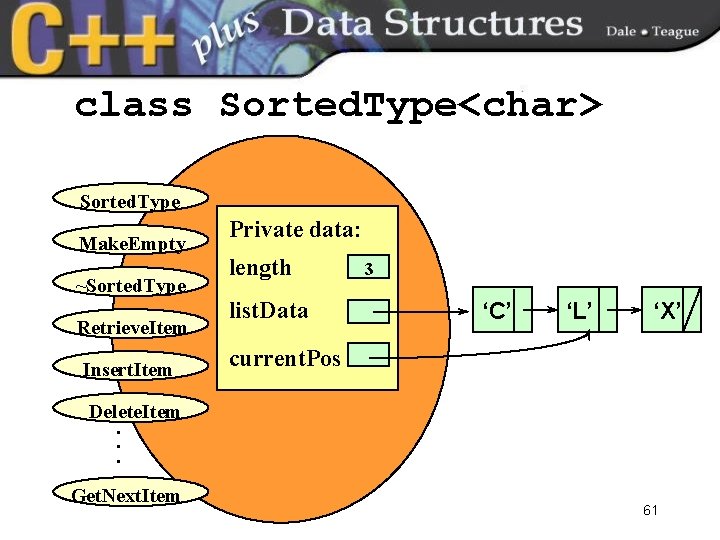
class Sorted. Type<char> Sorted. Type Make. Empty ~Sorted. Type Retrieve. Item Insert. Item Private data: length list. Data 3 ‘C’ ‘L’ ‘X’ current. Pos Delete. Item. . . Get. Next. Item 61

Insert. Item algorithm for Sorted Linked List • Find proper position for the new element in the sorted list using two pointers pred. Loc and location, where pred. Loc trails behind location. • Obtain a node for insertion and place item in it. • Insert the node by adjusting pointers. • Increment length. 62

Implementing Sorted. Type member function Insert. Item // LINKED LIST IMPLEMENTATION #include “Item. Type. h” (sorted. cpp) template <class Item. Type> void Sorted. Type<Item. Type> : : Insert. Item ( Item. Type item ) // Pre: List has been initialized. List is not full. item is not in list. // List is sorted by key member. // Post: item is in the list. List is still sorted. {. . . } 63

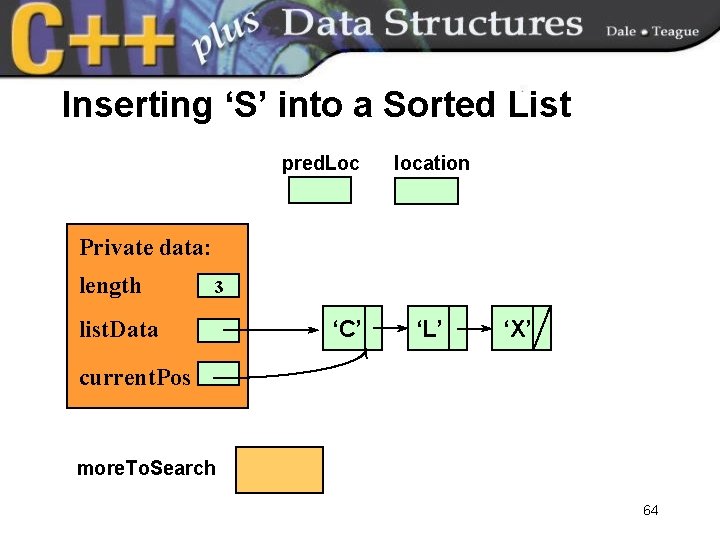
Inserting ‘S’ into a Sorted List pred. Loc location Private data: length 3 list. Data ‘C’ ‘L’ ‘X’ current. Pos more. To. Search 64

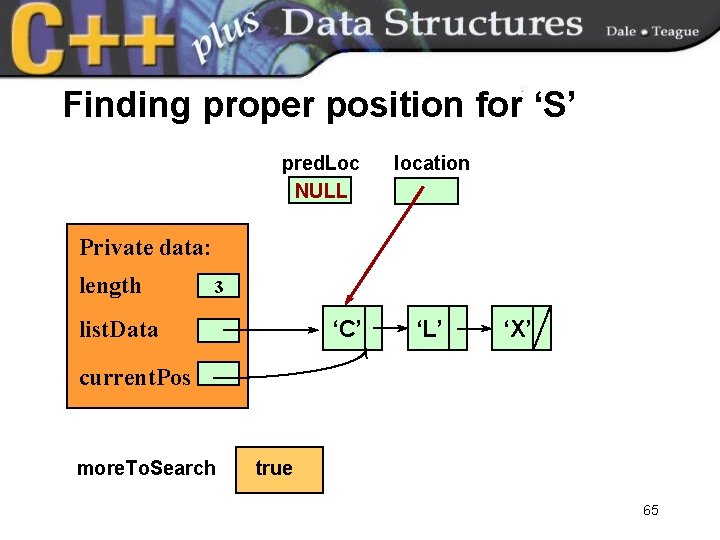
Finding proper position for ‘S’ pred. Loc NULL location Private data: length 3 list. Data ‘C’ ‘L’ ‘X’ current. Pos more. To. Search true 65

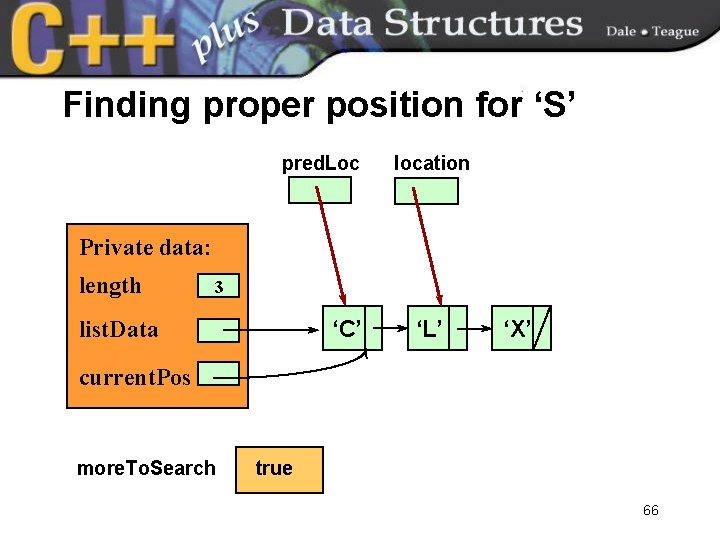
Finding proper position for ‘S’ pred. Loc location Private data: length 3 list. Data ‘C’ ‘L’ ‘X’ current. Pos more. To. Search true 66

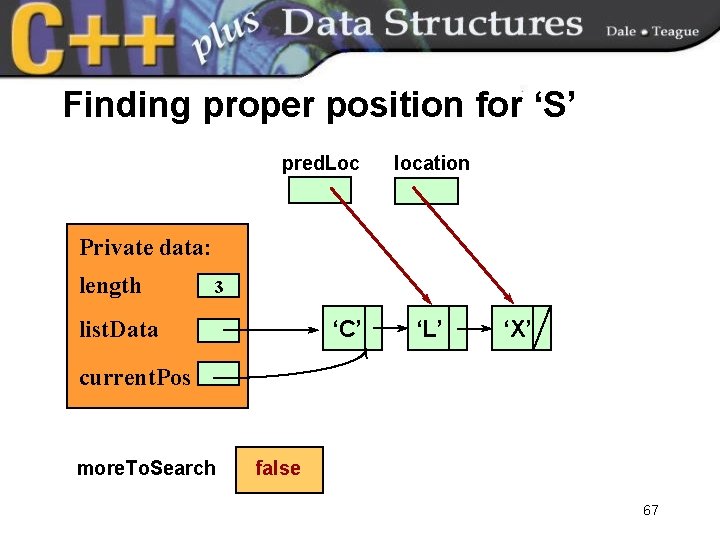
Finding proper position for ‘S’ pred. Loc location Private data: length 3 list. Data ‘C’ ‘L’ ‘X’ current. Pos more. To. Search false 67

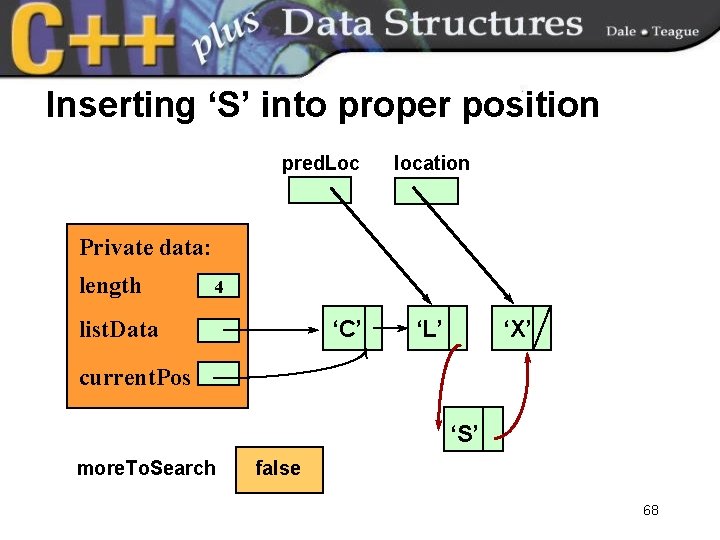
Inserting ‘S’ into proper position pred. Loc location Private data: length 4 list. Data ‘C’ ‘L’ ‘X’ current. Pos ‘S’ more. To. Search false 68