C Plus Data Structures Nell Dale Chapter 8

C++ Plus Data Structures Nell Dale Chapter 8 Binary Search Trees Modified from the slides by Sylvia Sorkin, Community College of Baltimore County - Essex Campus 1

Binary search for an element in a sorted list stored sequentially l l in an array: O(Log 2 N) in a linked list: ? (midpoint = ? ) 2

Goals of this chapter l Introduce some basic tree vocabulary l Develop algorithms l Implement operations needed to use a binary search tree 3

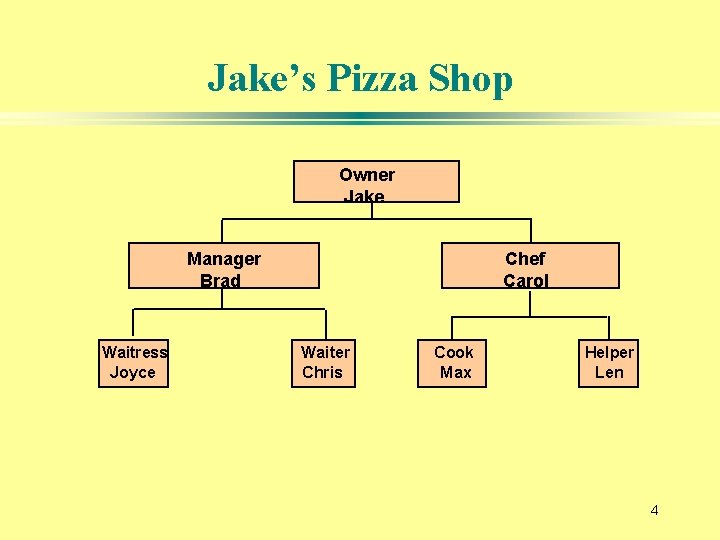
Jake’s Pizza Shop Owner Jake Manager Brad Waitress Joyce Chef Carol Waiter Chris Cook Max Helper Len 4

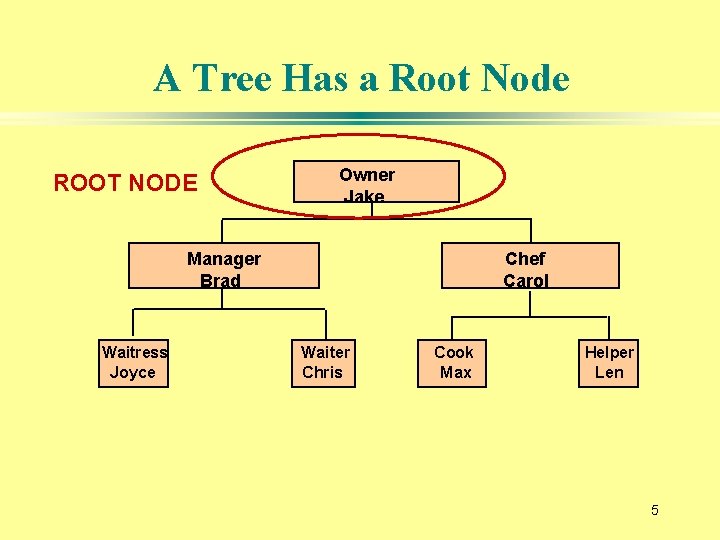
A Tree Has a Root Node ROOT NODE Owner Jake Manager Brad Waitress Joyce Chef Carol Waiter Chris Cook Max Helper Len 5

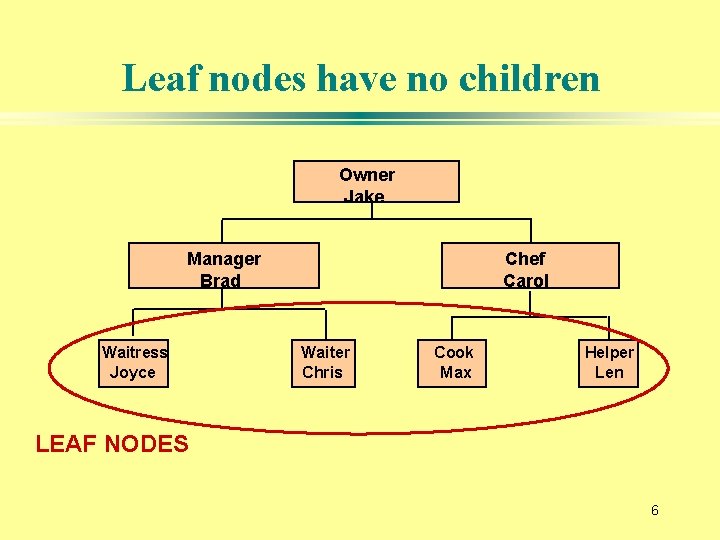
Leaf nodes have no children Owner Jake Manager Brad Waitress Joyce Chef Carol Waiter Chris Cook Max Helper Len LEAF NODES 6

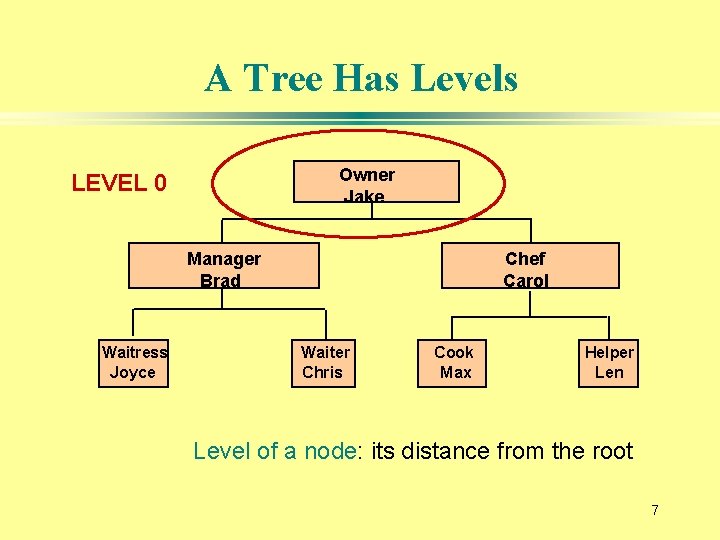
A Tree Has Levels Owner Jake LEVEL 0 Manager Brad Waitress Joyce Chef Carol Waiter Chris Cook Max Helper Len Level of a node: its distance from the root 7

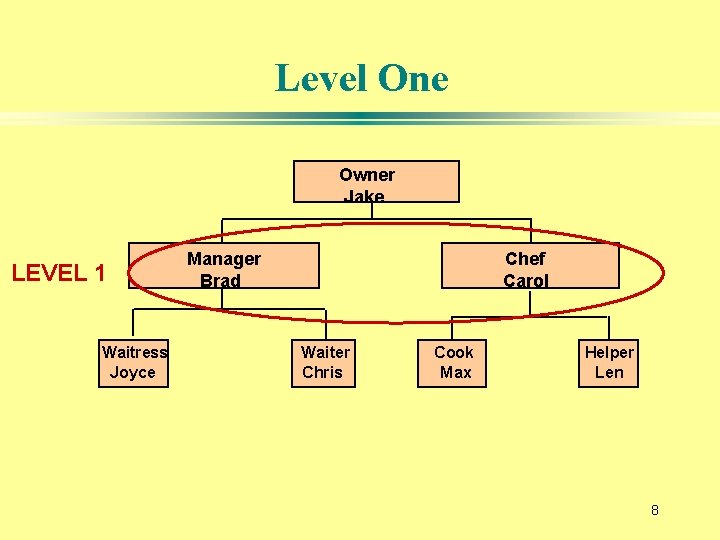
Level One Owner Jake LEVEL 1 Waitress Joyce Manager Brad Chef Carol Waiter Chris Cook Max Helper Len 8

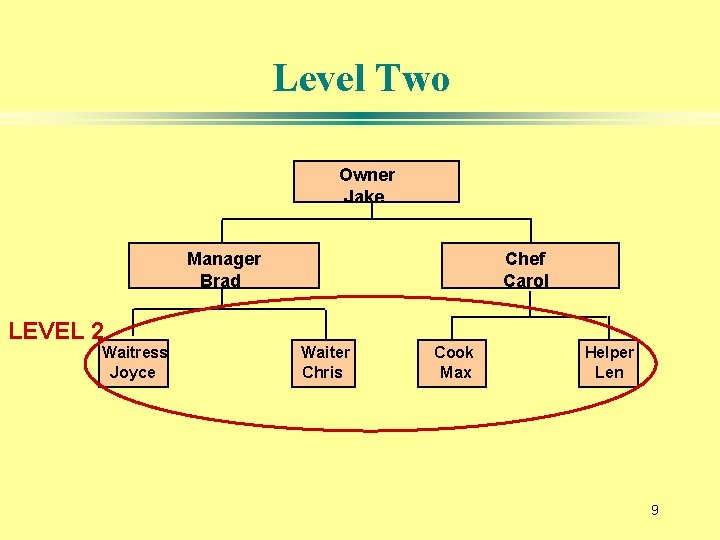
Level Two Owner Jake Manager Brad LEVEL 2 Waitress Joyce Chef Carol Waiter Chris Cook Max Helper Len 9

A binary tree with N nodes: l Maximum number of levels: N l Minimum number of levels: log. N + 1 e. g. , N=8, 16, …, 1000 10

The height of a tree: the maximum level in a tree -- a critical factor in determining how efficiently we can search for elements 11

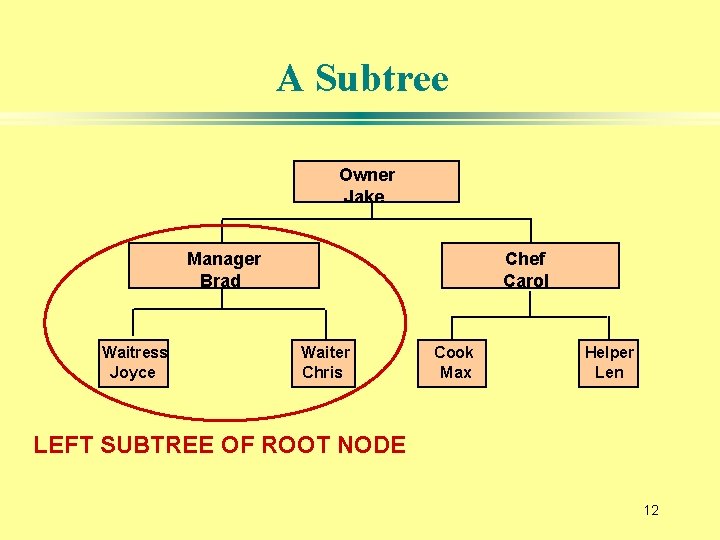
A Subtree Owner Jake Manager Brad Waitress Joyce Chef Carol Waiter Chris Cook Max Helper Len LEFT SUBTREE OF ROOT NODE 12

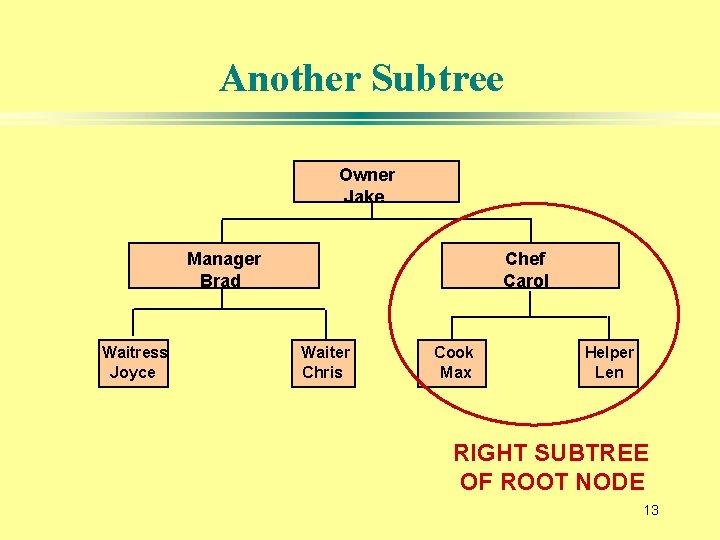
Another Subtree Owner Jake Manager Brad Waitress Joyce Chef Carol Waiter Chris Cook Max Helper Len RIGHT SUBTREE OF ROOT NODE 13

Binary Tree A binary tree is a structure in which: Each node can have at most two children, and in which a unique path exists from the root to every other node. The two children of a node are called the left child and the right child, if they exist. 14

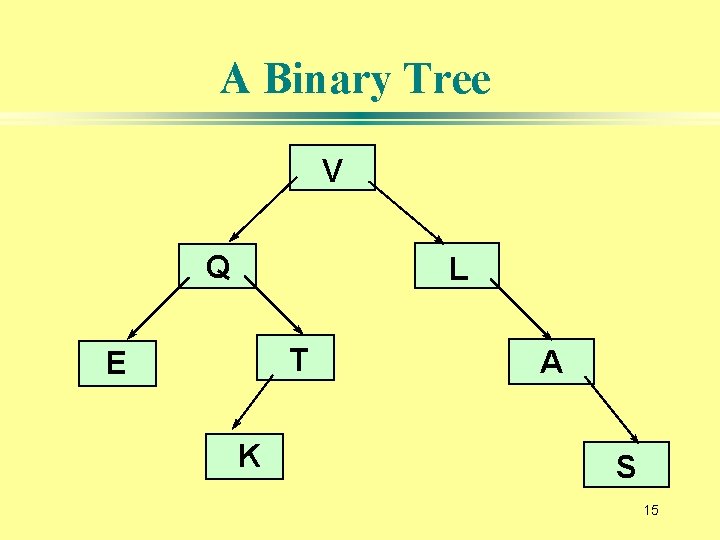
A Binary Tree V Q L T E K A S 15

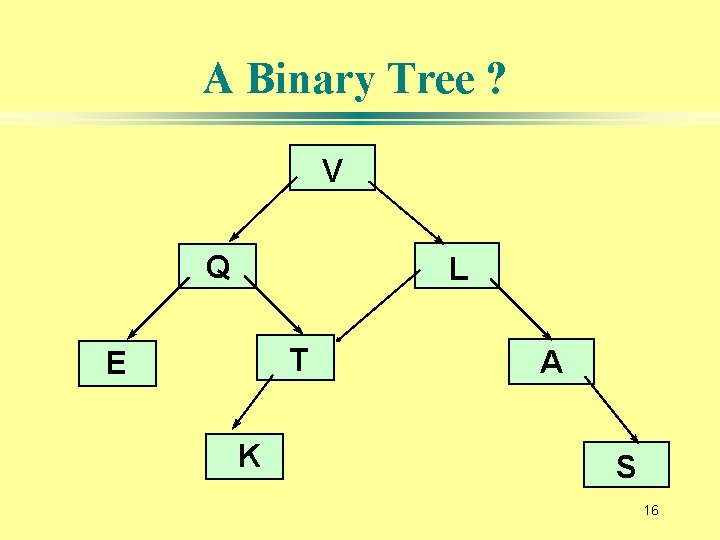
A Binary Tree ? V Q L T E K A S 16

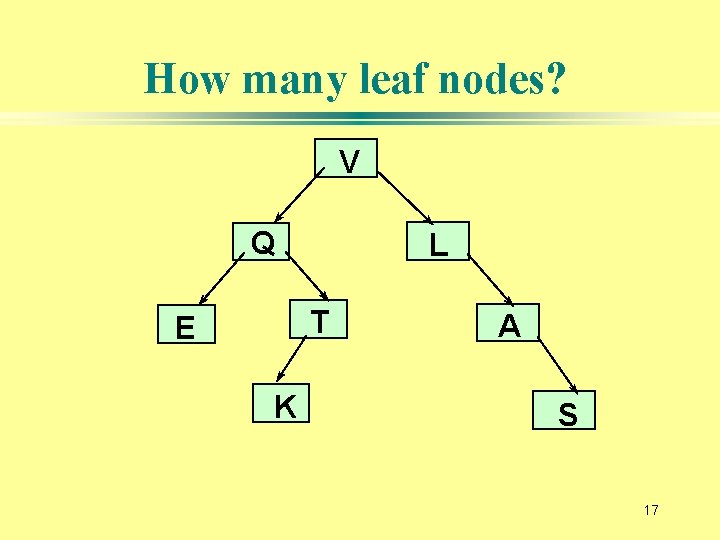
How many leaf nodes? V Q L T E K A S 17

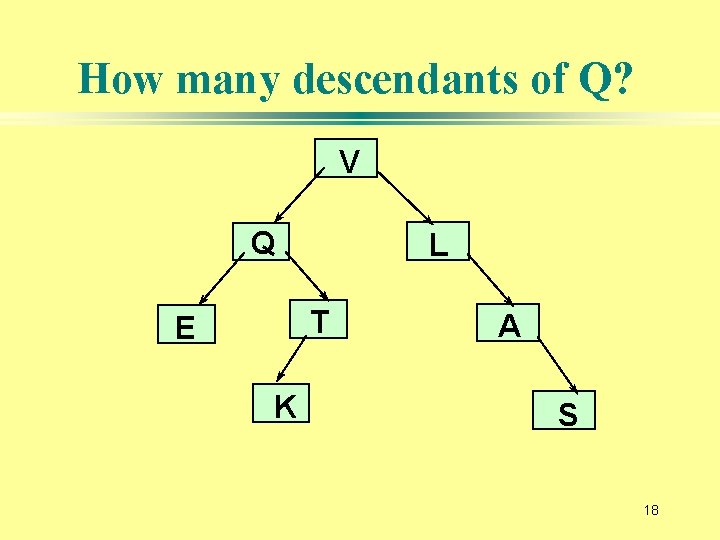
How many descendants of Q? V Q L T E K A S 18

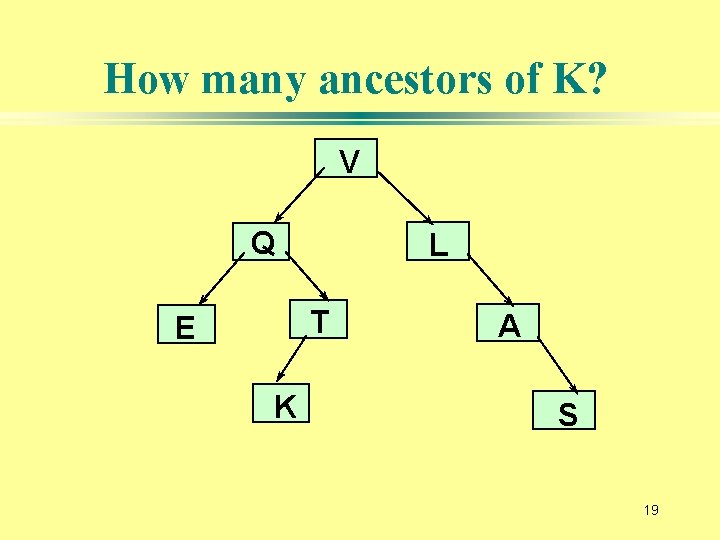
How many ancestors of K? V Q L T E K A S 19

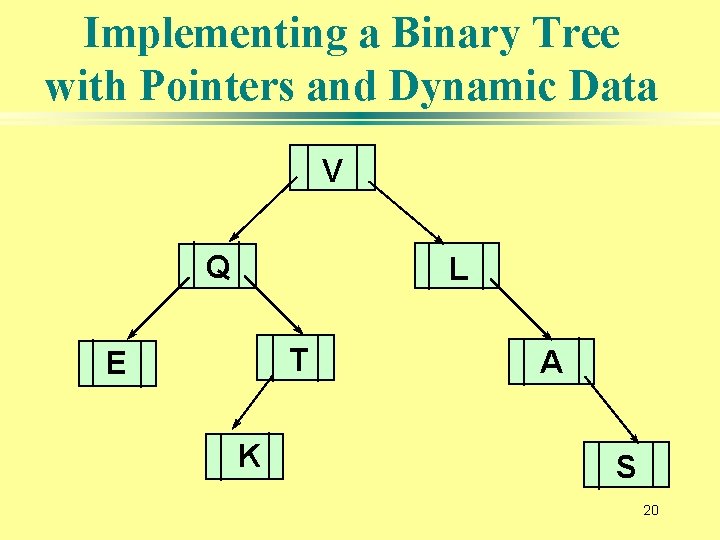
Implementing a Binary Tree with Pointers and Dynamic Data V Q L T E K A S 20

Each node contains two pointers template< class Item. Type > struct Tree. Node { Item. Type info; // Data member Tree. Node<Item. Type>* left; // Pointer to left child Tree. Node<Item. Type>* right; // Pointer to right child }; NULL. left ‘A’ 6000 . info . right 21

// BINARY SEARCH TREE SPECIFICATION template< class Item. Type > class Tree. Type { public: Tree. Type ( ); // constructor ~Tree. Type ( ); // destructor bool Is. Empty ( ) const; bool Is. Full ( ) const; int Number. Of. Nodes ( ) const; void Insert. Item ( Item. Type item ); void Delete. Item (Item. Type item ); void Retrieve. Item ( Item. Type& item, bool& found ); void Print. Tree (ofstream& out. File) const; . . . private: Tree. Node<Item. Type>* root; }; 22

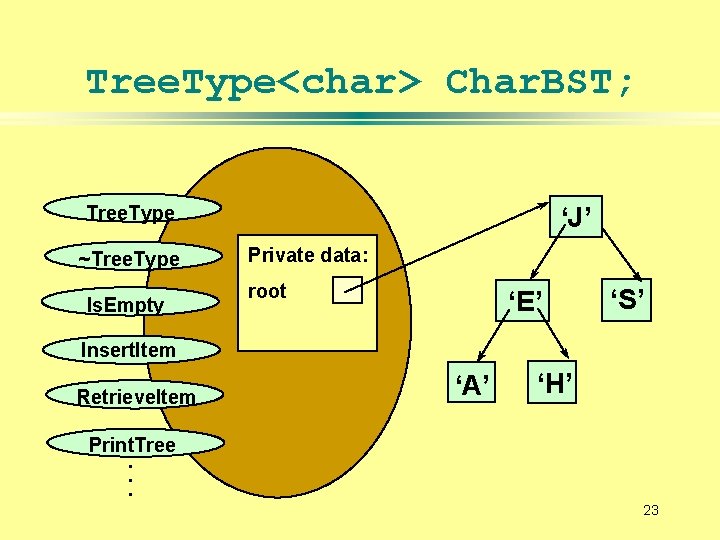
Tree. Type<char> Char. BST; ‘J’ Tree. Type ~Tree. Type Is. Empty Private data: root ‘E’ ‘S’ Insert. Item Retrieve. Item ‘A’ ‘H’ Print. Tree. . . 23

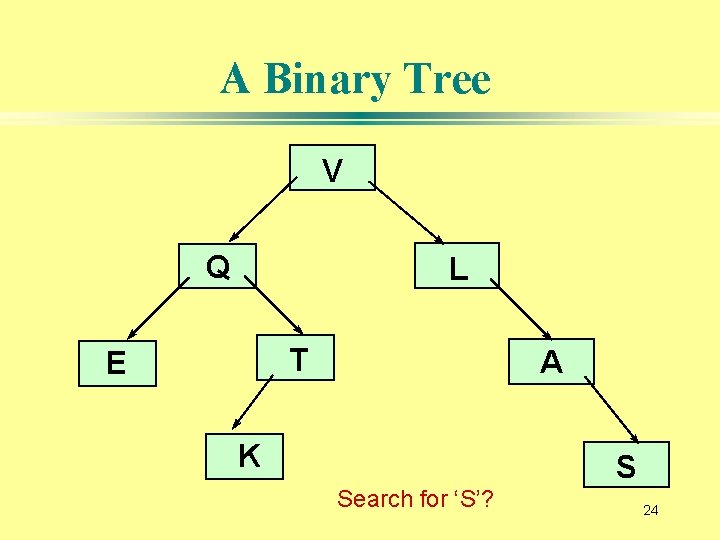
A Binary Tree V Q L T E A K S Search for ‘S’? 24

A Binary Search Tree (BST) is. . . A special kind of binary tree in which: 1. Each node contains a distinct data value, 2. The key values in the tree can be compared using “greater than” and “less than”, and 3. The key value of each node in the tree is less than every key value in its right subtree, and greater than every key value in its left subtree. 25

Shape of a binary search tree. . . Depends on its key values and their order of insertion. Insert the elements ‘J’ ‘E’ ‘F’ ‘T’ ‘A’ in that order. The first value to be inserted is put into the root node. ‘J’ 26

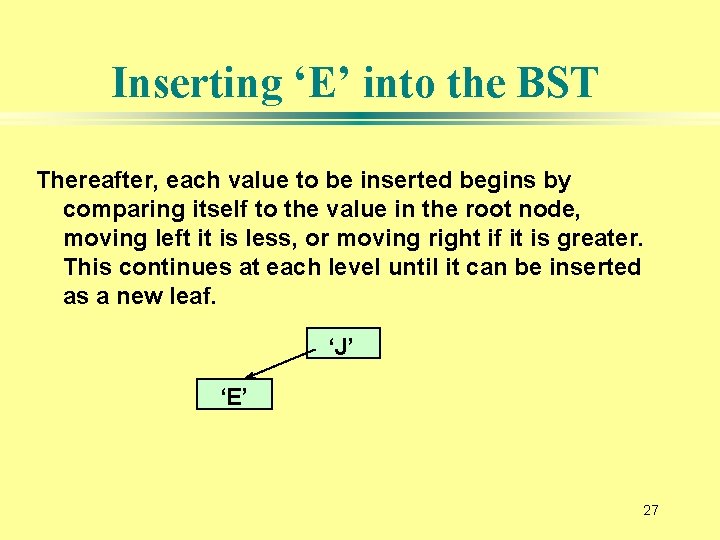
Inserting ‘E’ into the BST Thereafter, each value to be inserted begins by comparing itself to the value in the root node, moving left it is less, or moving right if it is greater. This continues at each level until it can be inserted as a new leaf. ‘J’ ‘E’ 27

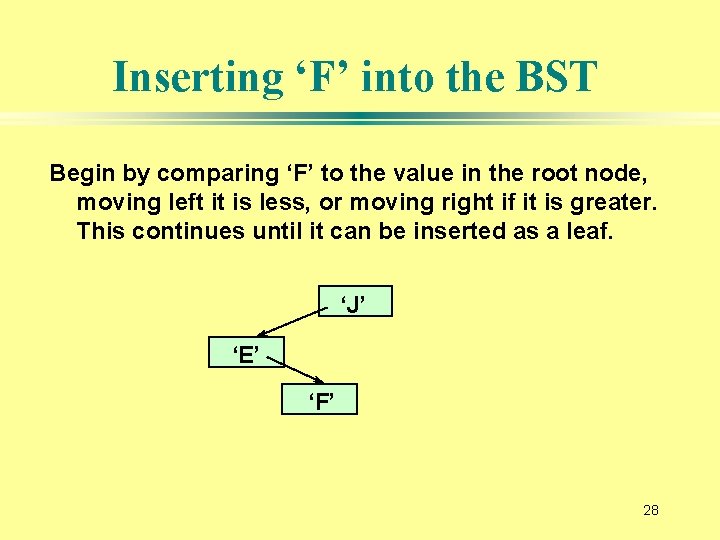
Inserting ‘F’ into the BST Begin by comparing ‘F’ to the value in the root node, moving left it is less, or moving right if it is greater. This continues until it can be inserted as a leaf. ‘J’ ‘E’ ‘F’ 28

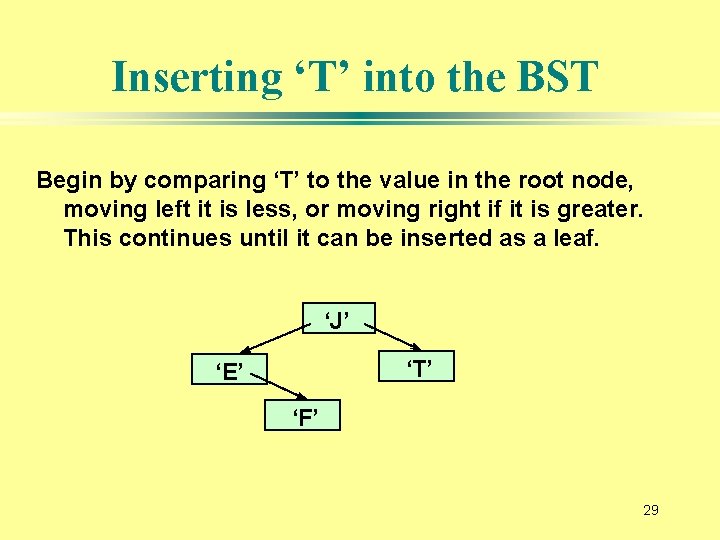
Inserting ‘T’ into the BST Begin by comparing ‘T’ to the value in the root node, moving left it is less, or moving right if it is greater. This continues until it can be inserted as a leaf. ‘J’ ‘T’ ‘E’ ‘F’ 29

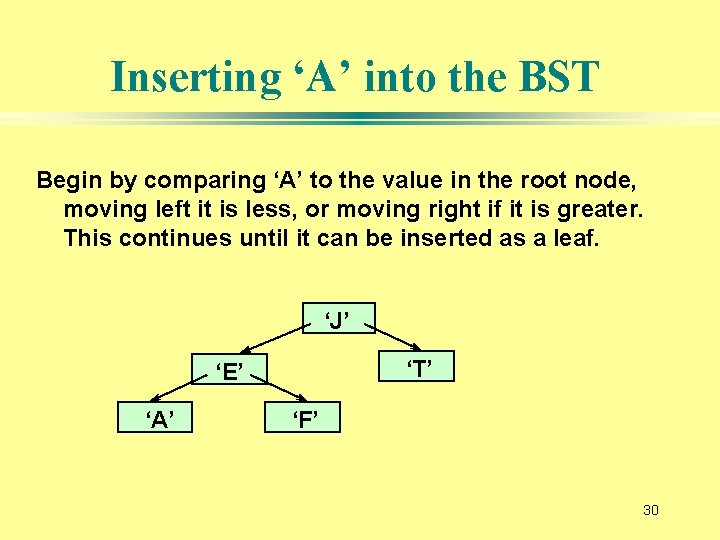
Inserting ‘A’ into the BST Begin by comparing ‘A’ to the value in the root node, moving left it is less, or moving right if it is greater. This continues until it can be inserted as a leaf. ‘J’ ‘T’ ‘E’ ‘A’ ‘F’ 30

What binary search tree. . . is obtained by inserting the elements ‘A’ ‘E’ ‘F’ ‘J’ ‘T’ in that order? ‘A’ 31

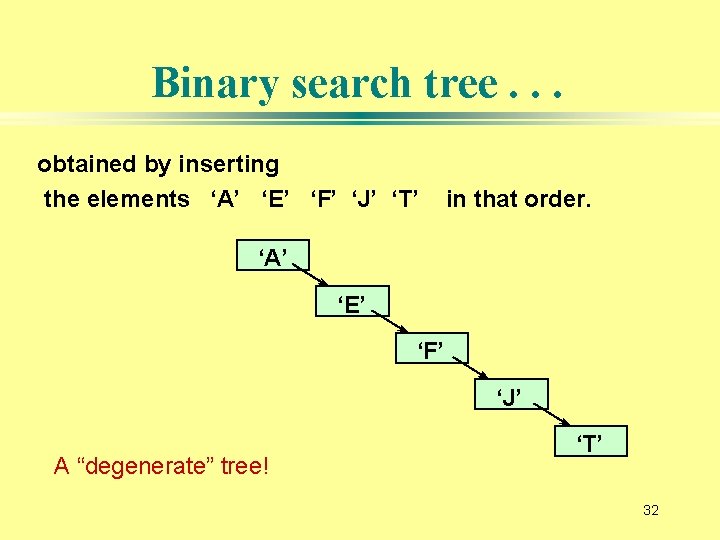
Binary search tree. . . obtained by inserting the elements ‘A’ ‘E’ ‘F’ ‘J’ ‘T’ in that order. ‘A’ ‘E’ ‘F’ ‘J’ A “degenerate” tree! ‘T’ 32

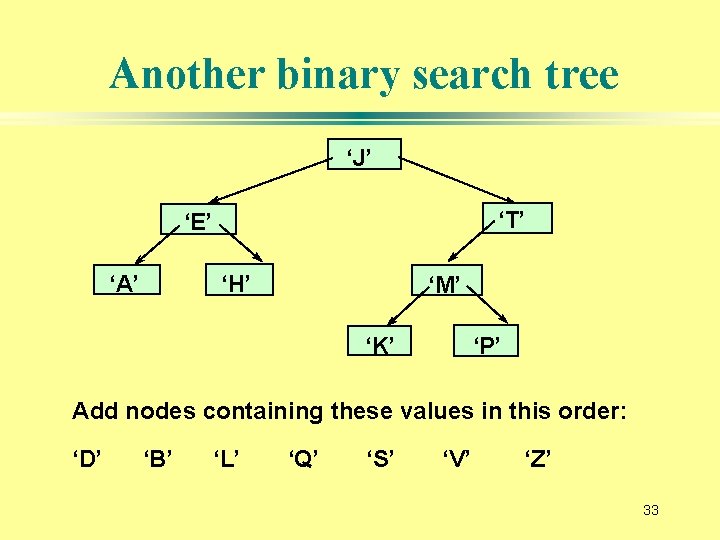
Another binary search tree ‘J’ ‘T’ ‘E’ ‘A’ ‘H’ ‘M’ ‘P’ ‘K’ Add nodes containing these values in this order: ‘D’ ‘B’ ‘L’ ‘Q’ ‘S’ ‘V’ ‘Z’ 33

// BINARY SEARCH TREE SPECIFICATION template< class Item. Type > class Tree. Type { public: Tree. Type ( ) ; // constructor ~Tree. Type ( ) ; // destructor bool Is. Empty ( ) const ; bool Is. Full ( ) const ; int Number. Of. Nodes ( ) const ; void Insert. Item ( Item. Type item ) ; void Delete. Item (Item. Type item ) ; void Retrieve. Item ( Item. Type& item , bool& found ) ; void Print. Tree (ofstream& out. File) const ; . . . private: Tree. Node<Item. Type>* root ; }; 35

// SPECIFICATION (continued) // - - - - - - - - - - - - - // RECURSIVE PARTNERS OF MEMBER FUNCTIONS template< class Item. Type > void Print. Helper ( Tree. Node<Item. Type>* ptr, ofstream& out. File ) ; template< class Item. Type > void Insert. Helper ( Tree. Node<Item. Type>*& ptr, Item. Type item ) ; template< class Item. Type > void Retrieve. Helper ( Tree. Node<Item. Type>* ptr, Item. Type& item, bool& found ) ; template< class Item. Type > void Destroy. Helper ( Tree. Node<Item. Type>* ptr ) ; 36

// BINARY SEARCH TREE IMPLEMENTATION // OF MEMBER FUNCTIONS AND THEIR HELPER FUNCTIONS // - - - - - - - - - - - - - template< class Item. Type > Tree. Type<Item. Type> : : Tree. Type ( ) // constructor { root = NULL ; } // - - - - - - - - - - - - - template< class Item. Type > bool Tree. Type<Item. Type> : : Is. Empty( ) const { return ( root == NULL ) ; } 37

template< class Item. Type > void Tree. Type<Item. Type> : : Retrieve. Item ( Item. Type& item, bool& found ) { Retrieve. Helper ( root, item, found ) ; } template< class Item. Type > void Retrieve. Helper ( Tree. Node<Item. Type>* ptr, Item. Type& item, bool& found) { if ( ptr == NULL ) found = false ; else if ( item < ptr->info ) // GO LEFT Retrieve. Helper( ptr->left , item, found ) ; else if ( item > ptr->info ) // GO RIGHT Retrieve. Helper( ptr->right , item, found ) ; else { // item = ptr->info ; found = true ; } 38 }

template< class Item. Type, class KF > void Tree. Type<Item. Type, KF> : : Retrieve. Item ( Item. Type& item, KF key, bool& found ) // Searches for an element with the same key as item’s key. // If found, store it into item { Retrieve. Helper ( root, item, key, found ) ; } template< class Item. Type > void Retrieve. Helper ( Tree. Node<Item. Type, KF>* ptr, Item. Type& item, KF key, bool& found) { if ( ptr == NULL ) found = false ; else if ( key < ptr->info. key() ) // GO LEFT Retrieve. Helper( ptr->left , item, key, found ) ; else if ( key > ptr->info. key() ) // GO RIGHT Retrieve. Helper( ptr->right , item, key, found ) ; else { item = ptr->info ; found = true ; } 39 }

template< class Item. Type > void Tree. Type<Item. Type> : : Insert. Item ( Item. Type item ) { Insert. Helper ( root, item ) ; } template< class Item. Type > void Insert. Helper ( Tree. Node<Item. Type>*& ptr, Item. Type item ) { if ( ptr == NULL ) { // INSERT item HERE AS LEAF ptr = new Tree. Node<Item. Type> ; ptr->right = NULL ; ptr->left = NULL ; ptr->info = item ; } else if ( item < ptr->info ) // GO LEFT Insert. Helper( ptr->left , item ) ; else if ( item > ptr->info ) // GO RIGHT Insert. Helper( ptr->right , item ) ; 40 }

Delete() l l l Find the node in the tree Delete the node from the tree Three cases: 1. Deleting a leaf 2. Deleting a node with only one child 3. Deleting a node with two children Note: the tree must remain a binary tree and the search property must remain intact 41

template< class Item. Type > void Tree. Type<Item. Type> : : Delete. Item ( Item. Type& item ) { Delete. Helper ( root, item ) ; } template< class Item. Type > void Delete. Helper ( Tree. Node<Item. Type>* ptr, Item. Type& item) { if ( item < ptr->info ) // GO LEFT Delete. Helper( ptr->left , item ) ; else if ( item > ptr->info ) // GO RIGHT Delete. Helper( ptr->right , item ) ; else { Delete. Node(ptr); // Node is found: call Delete. Node } } 42

template< class Item. Type > void Delete. Node ( Tree. Node<Item. Type>*& tree ) { Item. Type data; Tree. Node< Item. Type>* temp. Ptr; temp. Ptr = tree; if ( tree->left == NULL ) { tree = tree->right; delete temp. Ptr; } else if (tree->right == NULL ) { tree = tree->left; delete temp. Ptr; } else { // have two children Get. Predecessor(tree->left, item); tree->info = item; Delete. Helper(tree->left, item); // Delete predecessor node (rec) } } 43

template< class Item. Type > void Get. Predecessor( Tree. Node<Item. Type>* tree, Item. Type& data ) // Sets data to the info member of the rightmost node in tree { while (tree->right != NULL) tree = tree->right; data = tree->info; } 44

Print. Tree() Traverse a list: -- forward -- backward Traverse a tree: -- there are many ways! 45

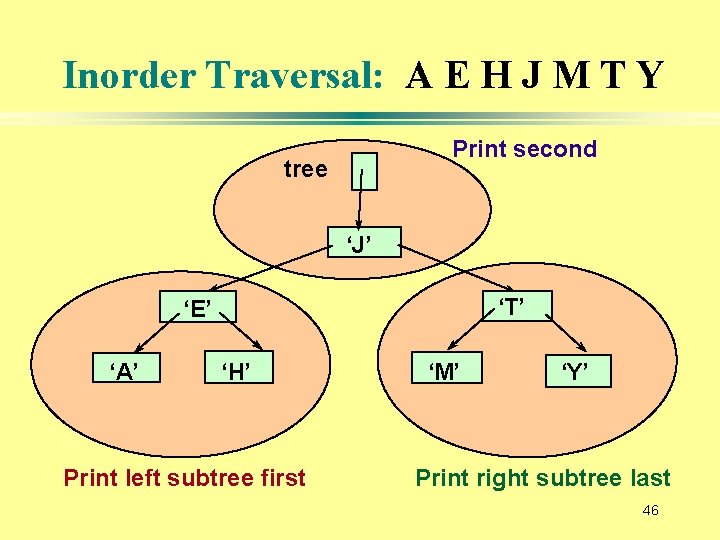
Inorder Traversal: A E H J M T Y Print second tree ‘J’ ‘T’ ‘E’ ‘A’ ‘H’ Print left subtree first ‘M’ ‘Y’ Print right subtree last 46

// INORDER TRAVERSAL template< class Item. Type > void Tree. Type<Item. Type> : : Print. Tree ( ofstream& out. File ) const { Print. Helper ( root, out. File ) ; } template< class Item. Type > void Print. Helper ( Tree. Node<Item. Type>* ptr, ofstream& out. File ) { if ( ptr != NULL ) { Print. Helper( ptr->left , out. File ) ; // Print left subtree out. File << ptr->info ; Print. Helper( ptr->right, out. File ) ; // Print right subtree } } 47

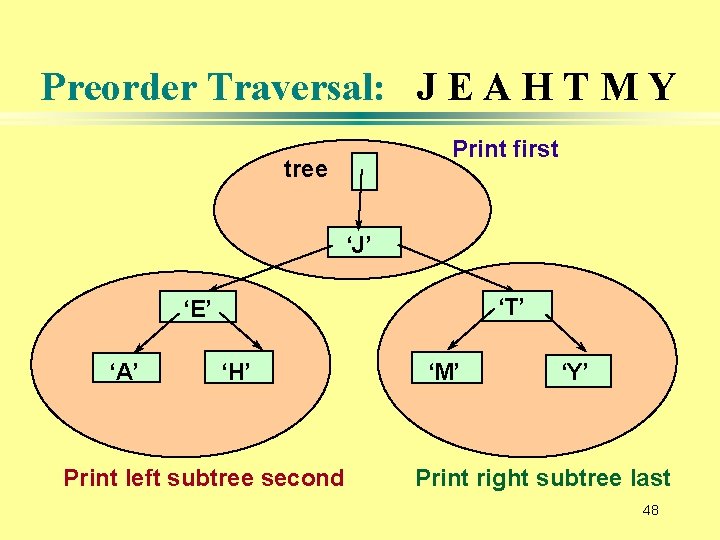
Preorder Traversal: J E A H T M Y Print first tree ‘J’ ‘T’ ‘E’ ‘A’ ‘H’ Print left subtree second ‘M’ ‘Y’ Print right subtree last 48

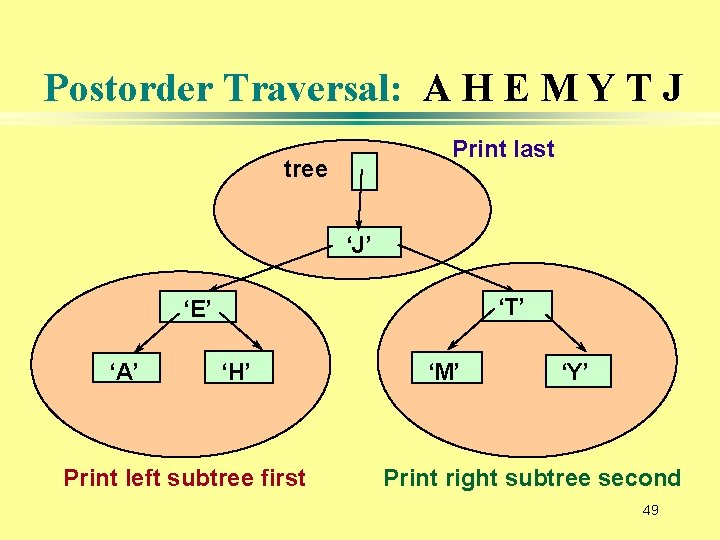
Postorder Traversal: A H E M Y T J Print last tree ‘J’ ‘T’ ‘E’ ‘A’ ‘H’ Print left subtree first ‘M’ ‘Y’ Print right subtree second 49

template< class Item. Type > Tree. Type<Item. Type> : : ~Tree. Type ( ) { Destroy. Helper ( root ) ; } // DESTRUCTOR template< class Item. Type > void Destroy. Helper ( Tree. Node<Item. Type>* ptr ) // Post: All nodes of the tree pointed to by ptr are deallocated. { if ( ptr != NULL ) { Destroy. Helper ( ptr->left ) ; Destroy. Helper ( ptr->right ) ; delete ptr ; } } 50

Iterative Insertion and Deletion Read Text … 51

Recursion or Iteration? Assume: the tree is well balanced. l l l Is the depth of recursion relatively shallow? Yes. Is the recursive solution shorter or clearer than the nonrecursive version? Yes. Is the recursive version much less efficient than the nonrecursive version? No. 52

Use a recursive solution when (Chpt. 7): l The depth of recursive calls is relatively “shallow” compared to the size of the problem. l The recursive version does about the same amount of work as the nonrecursive version. l The recursive version is shorter and simpler than the nonrecursive solution. SHALLOW DEPTH EFFICIENCY CLARITY 53

Binary Search Trees (BSTs) vs. Linear Lists BST: l l Quick random-access with the flexibility of a linked structure Can be implemented elegantly and concisely using recursion Takes up more memory space than a singly linked list Algorithms are more complicated 54

End 55