C MetaProgramming Concepts and Results Walter E Brown

C++ Meta<Programming> Concepts and Results Walter E. Brown WB@fnal. gov f Fermi National Accelerator Laboratory C++ Meta<Programming>

What is Metaprogramming? f “The art of programming programs that read, transform, or write other programs. ” - François-René Rideau Let’s dream for a moment: Suppose we could programs that can “transform” themselves …. It’s not a dream: Via templates, we can do exactly that in modern C++! 10 April 2001 C++ Meta<Programming> 2

f Overview w Concepts: • Generalized parameterization via C++ templates • Kinds of templates; kinds of template parameters w Selected results: • Meta-algorithms & generic programming • Templates as general computation engines: § Compile-time computation § Type computations § Compile-time control structures for selection & looping • Meta-coding and -debugging methodologies • Performance 10 April 2001 C++ Meta<Programming> 3

Review of Classical Parameterization f w Function behavior is traditionally expressed in terms of placeholder objects, parameters: double square( double x ) { return x * x; } w Specific values (arguments) are supplied (passed) when the function is invoked: … square( -3. 14 ) … w Such parameter passage: • Happens at run-time • Uses copy semantics to initialize parameters 10 April 2001 C++ Meta<Programming> 4

Generalized Parameterization f w Modern C++ also provides compile-time placeholders, e. g. , type parameters: template< typename T > inline T square( T x ) { return x * x; } w Compiler processes such a function template: • • Semantics akin to text substitution: instantiation Yields a specialization (argument-specific version) Specialization compiled & used as a function No further use of template 10 April 2001 C++ Meta<Programming> 5

Specialization Details f w A specialization is instantiated iff needed: … square<double>( -3. 14 ) … w Template arguments may be deduced from the function arguments: square( -3. 14 ); // implies square<double>(…) My. Type m = … ; square( m ); // implies square<My. Type>(…) w We can define our own specializations: template<> // alternate algorithm for My. Type double square<My. Type>( My. Type x ) { … } 10 April 2001 C++ Meta<Programming> 6

Example: swap<>( ) from <algorithm> f w Usual algorithm, but couched generically (i. e. , a meta-algorithm, applicable to many types): template< typename T > inline void swap( T & x, T & y ) { T const tmp( x ); x = y; y = tmp; } w Note reliance on T’s concepts (properties): • In above, T must be copyable and assignable • Compile-time enforcement (concept-checking) techniques available 10 April 2001 C++ Meta<Programming> 7

Generic Programming Pitfalls f w Extra thought is necessary when designing generic components: template< typename X, typename Y > // No! void swap( X & x, Y & y ) { X const tmp( x ); x = y; y = tmp; } w Relies on X Y conversion concepts: • Post-swap() values need not match original values • Hence, swap() twice can’t always restore originals • Such counter-intuitive behavior ought be avoided 10 April 2001 C++ Meta<Programming> 8

Class Templates f w Example from <complex>: template< class T > class complex { public: complex( T r, T i ) : realpart(r), imagpart(i) { } T real() const { return realpart; } // … more member functions … private: T realpart, imagpart; }; w Usage: complex< double > c; 10 April 2001 C++ Meta<Programming> 9

Class Template Details f w Each function member is a function template: • Each is independently instantiated, iff needed • Its template parameters match those of the class • May have its own (additional) template parameters w Common practice is to publish each class template’s arguments: template< class T > class Container { public: typedef T value_type; // … }; 10 April 2001 C++ Meta<Programming> 10

Unlike Function Templates … f w Class template arguments can’t be deduced in the same way, so usually written explicitly: complex <double> c; w Class template parameters may have default values: template< class T, class U = int > class My. Cls { … }; w Class templates may be partially specialized: template< class U > class My. Cls< bool, U > { … }; 10 April 2001 C++ Meta<Programming> 11

Using Specializations f w First declare (and/or define) the general case: template< class T > class C { /* handle most types this way */ }; w Then provide either or both kinds of special cases as desired: template< class T > class C< T * > { /* handle pointers specially */ }; template<> // note: fully specialized class C< int * > { /* treat int pointers thusly */ }; w Compiler will select the most specialized applicable class template 10 April 2001 C++ Meta<Programming> 12

f Shims w Useful for certain kinds of boilerplate code, e. g. , a polymorphic clone( ) function: class Mine : public Parent { virtual Mine * clone( ) const { return new Mine(*this); } }; w Awkward to maintain in a hierarchy: • Are all clone( ) functions equivalent to begin with? • Now change all return types to Base. Cls *, or use std: : auto_ptr<>, or add non-const versions, or … • Will need to find and update each occurrence • Did we get them all? Are they really consistent? 10 April 2001 C++ Meta<Programming> 13

f Shims (cont’d) w Introduce clone shims into the hierarchy: class Mine : public Clone. Shim< Mine , Parent > { … }; class Yours : public Clone. Shim< Yours, Mine > { … }; w All clone shims arise from one class template: template< class D, class B > struct Clone. Shim : public B { // … constructors … virtual D * clone( ) const { return new D( * (D*)this ); } }; w Result: a single point of code maintenance! 10 April 2001 C++ Meta<Programming> 14

f Generic Algorithms with User Plug-ins w Functor: a class with an operator( ) member w Functors and functions are compatible: void fn( float x ) { … } struct Ftor { void operator( ) ( float x ) { … } }; w A generic algorithm can call either kind: template< typename Func > void algo( Func f, float q ) { f(q); } // Sample invocations of generic algorithm: algo( fn, -3. 14 ); algo( Ftor( ), -3. 14 ); OR Ftor f; algo( f, -3. 14 ); 10 April 2001 C++ Meta<Programming> 15

Non-type Template Parameters f w Non-type parameters include: • Integral, enum. types: int, long, bool, enum, … • Pointer types: int *, std: : string *, void (*)( int ), … w Example: template< unsigned N > inline double pow( double x ) { double ans( 1. 0 ); for ( unsigned k = 0; k < N; ++k ) ans *= x; return ans; } 10 April 2001 C++ Meta<Programming> 16

An Improved Algorithm f w Based on mathematical identity x. N = (x 2)(N/2) w Time complexity O(log 2 N) vs. prior O(N): template< unsigned N > inline double pow( double x ) { return pow<N % 2>( x ) * pow<N / 2>( x * x ); } template<> inline double pow<1 u>( double x ) { return x; } template<> inline double pow<0 u>( double x ) { return 1. ; } 10 April 2001 C++ Meta<Programming> 17

f Representative Timings std: : pow() pow<>() v 1 pow<>() v 2 real 11. 858 s 8. 081 s 3. 035 s user 11. 837 s 8. 081 s 3. 024 s sys 0. 020 s 0. 030 s w Based on x 50 repeated 10, 000 times w Using gcc 2. 95. 2 on 700 MHz PIII, Win 2 K 10 April 2001 C++ Meta<Programming> 18

f Timings with Optimization std: : pow() pow<>() v 1 pow<>() v 2 real 11. 857 s 4. 286 s 0. 300 s user 11. 847 s 4. 236 s 0. 190 s sys 0. 020 s 0. 010 s w Using g++ -O 2 to compile; otherwise same w Improvements: ~47% for v 1; ~90% for v 2! 10 April 2001 C++ Meta<Programming> 19

f Why? “[Use of ] templates will often result in code that is orders of magnitude faster (because costs are pushed to compile time). ” - Francis Glassborow “Most of the win … comes from the additional optimization possibilities that are opened up. ” - James Kanze 10 April 2001 C++ Meta<Programming> 20

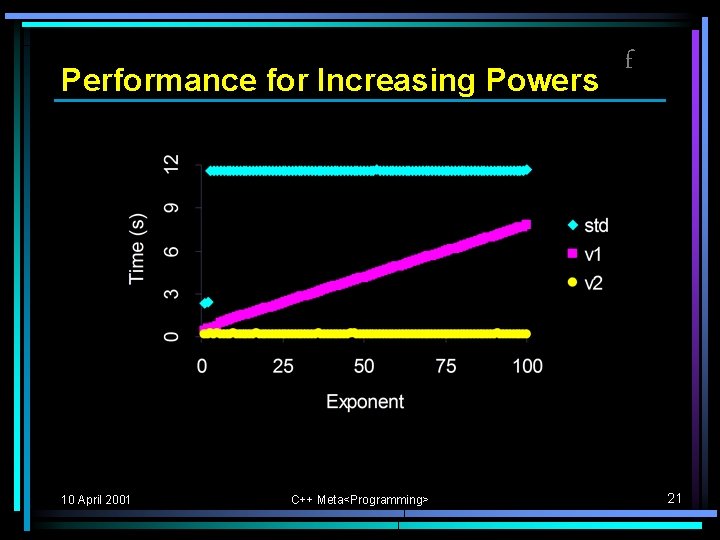
Performance for Increasing Powers 10 April 2001 C++ Meta<Programming> f 21

Template Parameters f w A class template can be a template argument w Example: template<class> class Bag > class C { // … Bag< float > b; }; w Or even: template< class E, template<class> class Bag > class C { // … Bag< E > b; }; 10 April 2001 C++ Meta<Programming> 22

Traits/Policies/Strategy/Behavior f w Common to generic programming: • Instantiation G<U> needs some service, guidance, or information from U • But G doesn’t know how to ask this of arbitrary U w Use non-intrusive, indirect adaptor Tr<>: • Typedef t or static member s of Tr<> provides an interface to the needed functionality or property • User will specialize Tr<U> for U‘s of interest • Instantiation G<U> uses Tr<U>: : s instead of U: : ? 10 April 2001 C++ Meta<Programming> 23

f Using Traits/Policies template< class > struct Ctraits; { // default traits template< class U, template<class> class Tr = Ctraits > class G { // generic algorithm typedef Tr<U>: : return_type; inline type operator( ) { return Tr<U>: : s( ); } }; template<> struct Ctraits<int> { // specialized traits typedef double return_type; static inline double s( ) { return 3. 14; } }; … G<int>( ) … // user application code 10 April 2001 C++ Meta<Programming> 24

Templates in Brief f w Summary so far: • Function templates and class templates • Type, non-type, template parameters • Traits, shims, functors, generic programming w Significant inherent computational power: • Realized only long after templates’ initial design: § Explains unfamiliar, somewhat awkward syntax § Is surprisingly powerful: Turing-completeness claimed • Exploited via meta-programming, advanced compile-time computation 10 April 2001 C++ Meta<Programming> 25

Compile-time Computation f w Compile-time absolute value: template< int N > struct Abs { // publish computed value: static int const ans = (N < 0) ? - N : N; }; w Usage: int const my. Num = …; Abs<my. Num>: : ans // now a compile-time const w We’ve barely begun the fun … 10 April 2001 C++ Meta<Programming> 26

Example: General Compile-time Decisions f w Consider a type computation: template< bool, class > struct IF { typedef … type; // publish resulting type }; w This leads to self-configuring code: • • • 10 April 2001 int const q = … ; // user’s configuration parameter // Now compiler makes decisions based on q’s value: IF< (q<0), int, unsigned >: : type k; // pick 1 of 2 types IF< (q<0), F, G >: : type( )( … ) // call 1 of 2 functors class D : // inherit from 1 of 2 base classes public IF< (q<0), B 1, B 2 >: : type { … }; C++ Meta<Programming> 27

IF<> Behind the Scenes f w Simplest to rely on partial specialization: template< bool c, class T, class F > struct IF { // general case; assumes condition c is true typedef T type; }; template< class T, class F > struct IF< false, T, F > { // special case for false condition typedef F type; }; w Alternate (long-winded) implementations are available for broken compilers 10 April 2001 C++ Meta<Programming> 28

Combining Some Ideas f w Compile-time greatest common divisor: template< int M, int N > class Gcd { // via Euclid’s method private: static int const m = Abs<M>: : ans, n = Abs<N>: : ans; typedef typename IF< ( n == 0 ) , Gcd. Last<m, n> // final step , Gcd. Next<m, n> // next step >: : type Step; public: static int const ans = Step: : ans; }; 10 April 2001 C++ Meta<Programming> 29

Gcd<>’s Helpers f w Take the next step of Euclid’s algorithm: template< int M, int N > struct Gcd. Next { static int const ans = Gcd< N, M % N >: : ans; }; w Interpret the result when done: template< int M, int > struct Gcd. Last { // Gcd<M, 0> static int const ans = (M == 0) ? 1 : M; }; 10 April 2001 C++ Meta<Programming> 30

Gcd<> v 2: One Fewer Helper f w Absorb Gcd. Next<> into main template: template< int M, int N > class Gcd { // via Euclid’s method private: static int const m = Abs<M>: : ans, n = Abs<N>: : ans; typedef typename IF< ( n == 0 ) , Gcd. Last<m, n> // final step , Gcd<n, m % n > // next step >: : type Step; public: static int const ans = Step: : ans; }; 10 April 2001 C++ Meta<Programming> 31

f Gcd<> v 3: Partial Spec. as 2 nd Helper template< int M, int N > class Gcd { // via Euclid’s method private: static int const m = Abs<M>: : ans, n = Abs<N>: : ans; public: static int const ans = Gcd< n, m%n >: : ans; }; template< int M > class Gcd<M, 0> { // final step; subsumes Gcd. Last<>, IF<> public: static int const ans = (M == 0) ? 1 : Abs<M>: : ans; }; 10 April 2001 C++ Meta<Programming> 32

Metaprogramming Issues f w Most of us have little experience with this style of programming: • Concepts are unfamiliar • Utility is unfamiliar • Thought processes are unfamiliar w Can the process be simplified, perhaps even become formulaic? • Yes! • Apply elementary theory of computation 10 April 2001 C++ Meta<Programming> 33

What is a Computation? (Simplified) f w Computer memory defines state: • Systematically read and concatenate all bits, then interpret as a (large!) binary number • Start-up gives an initial state • Now any change in memory yields a new state w A computation transforms state. Init ® state. Final: • Typically composed of a sequence of steps, each itself a (sub-)computation • Commonly realized (of course!) via hardware • Each step (instruction) triggers a side effect (memory write) when carried out (executed) 10 April 2001 C++ Meta<Programming> 34

f Class State w A class’ state has traditionally been equated with its data members’ values: • This is run-time state, for execution may change it • If no data members, the class is deemed stateless w A class’ compile-time state is given by: • Internal type names (typedefs or nested classes) • Internally initialized data members (static integral or enum. consts) 10 April 2001 C++ Meta<Programming> 35

Example of Class State f template< class T = double > class Multiplier { public: // compile-time state: typedef T value_type; static int const t_size = sizeof( T ); Multiplier( T const & factor ) : m(factor) { } T operator( ) ( T const & x ) { return m * x; } private: // run-time state: T m; }; 10 April 2001 C++ Meta<Programming> 36

Compile-Time Iteration f w Design based on the C++ run-time for statement as a general looping model w Semantics based on 4 user-supplied parts: • • Initialization: a distinguished start state Condition: a state®bool mapping Body: a state®state mapping Reinitialization: another state®state mapping w So a for-loop maps a 4 -tuple to a (final) state 10 April 2001 C++ Meta<Programming> 37

Mantra for Compile-Time Loop State f w Use a class template with one parameter in place of each desired variable w Publish all the parameters w Example: template< int const N, long Prod=1, int K=N > struct State { static int const n = N; static long const prod = Prod; static int const k = K; }; 10 April 2001 C++ Meta<Programming> 38

Mantra for Compile-Time Loop Condition f w Use a class template whole sole parameter (say, S) is a state w Publish ans, a boolean result calculated from S’s published values w Example: template< class S > struct Cond { static bool const ans = ( S: : k > 0 ); }; 10 April 2001 C++ Meta<Programming> 39

Mantra for Compile-Time State®Statef Map w Use a class template whole sole parameter (say, S) is the initial state w Publish Next. State: : type, the successor state, computing its template arguments from S’s published values w Trivial (but useful!) example: template< class S > struct Do. Nothing { struct Next. State { typedef S type; }; }; 10 April 2001 C++ Meta<Programming> 40

More State®State Map Examples f // for reference: State< int const N, long Prod, int k > template< class S > struct Body { struct Next. State { typedef State< S: : n , S: : prod * S: : k , S: : k > type; }; }; template< class S > struct Reinit { struct Next. State { typedef State< S: : n , S: : prod , S: : k - 1 > type; }; }; 10 April 2001 C++ Meta<Programming> 41

A Convenient Wrapper using For<> f template< int N > struct Factorial { private: typedef typename For< State<N> , Pred , Reinit , Body >: : type Final. State; public: static long const ans = Final. State: : prod; }; // usage: Factorial<10>: : ans // now a compile-time constant! 10 April 2001 C++ Meta<Programming> 42

f How to Test? w First thought: std: : cout << "0! = " << Factorial< 0 >: : ans << ‘n’; std: : cout << “ 1! = " << Factorial< 1 >: : ans << ‘n’; std: : cout << “ 2! = " << Factorial< 2 >: : ans << ‘n’; std: : cout << “ 3! = " << Factorial< 3 >: : ans << ‘n’; std: : cout << “ 4! = " << Factorial< 4 >: : ans << ‘n’; std: : cout << “ 5! = " << Factorial< 5 >: : ans << ‘n’; w Observation: this is repetitive! w Would prefer to let the compiler generate it: Test. Factorial<5>( ); // this works! 10 April 2001 C++ Meta<Programming> 43

Using For<> to Generate Code f w Initial state: • Initialize const target n per argument • Initialize counter k = 0 • Provide constructor body with code prototype w Predicate: k <= n w Reinitialization: increment k w Body: nothing to do, so just use Do. Nothing<>! w Wrapper: instantiate the loop in the constructor 10 April 2001 C++ Meta<Programming> 44

Code Generation Loop Parts f template< int const N, int K=0 > struct Fact. Test. State { static int const n = N; static int const k = K; Test. Fact. State( ) { // constructor std: : cout << K << "! = " << Factorial<K>: : ans << 'n'; } }; template< class S > struct Fact. Test. Pred { static bool const ans = ( S: : k <= S: : n ); }; template< class S > struct Fact. Test. Reinit { struct Next. State { typedef Test. Fact. State< S: : n , 1 + S: : k > type; }; }; 10 April 2001 C++ Meta<Programming> 45

Code Generation Wrapper f template< int N > struct Factorial. Test { typedef typename For< Fact. Test. State<N> , Fact. Test. Pred , Fact. Test. Reinit , Do. Nothing > Loop; Test. Fact( ) { Loop( ); } // constructor }; 10 April 2001 C++ Meta<Programming> 46

Metaprogramming’s Memory Usage f w Code space: • Function templates are only instantiated if called • Use of IF<> can reduce necessary instantiations • Code optimization opportunities are plentiful w Data space: • It’s like coding 1 + 2: the object code has only a 3 • Class templates, even if instantiated, seldom leave any memory footprint for data w “Bloat” is very often an artifact of inexperience 10 April 2001 C++ Meta<Programming> 47

f Metaprogramming’s Use of CPU Time w Build time may increase somewhat: • Compiler is doing (considerably) more work • Compile time often supplants execution time w Build time may decrease somewhat: • Unused code is not compiled • Better inlining decreases link time 10 April 2001 C++ Meta<Programming> 48

Overall Metaprogramming Efficiency f w Many programmers confuse efficiency with performance: • A program giving the wrong answer at the speed of light is fast, but certainly not efficient! • Efficiency is correctly measured as a weighted sum of all relevant costs w Yes, metaprogramming can certainly be an important source of improved performance • Unfamiliar, so has a longish learning curve for now • Rapidly becoming increasingly important in modern programming 10 April 2001 C++ Meta<Programming> 49

For More Information f w C++ language: • Koenig & Moo: Accelerated C++, 2000 • Stroustrup: The C++ Programming Language, Special Edition, 2000 w C++ programming technique: • www. boost. org: “Generic Programming Techniques, ” 2001 • Alexandrescu: Modern C++ Design, 2001 • Czarnecki & Eisenecker: Generative Programming, 2000 10 April 2001 C++ Meta<Programming> 50

f Commercial #1 w Brown: Meta • Support library (headers) to facilitate C++ metaprogramming • Experimental version now available for CVS checkout via Zoom project • No documentation yet, but lots of test programs • Works with: § KAI 4. 0 d under Irix § gcc 2. 95. 3 + STLport 4. 1 b 5 library under Cygwin/Win 2 K 10 April 2001 C++ Meta<Programming> 51

f Commercial #2 w Brown: SIunits: the Library of Unit-Based Computation • • Extensive application of C++ metaprogramming New release in preparation Being adopted by JPL Seeking summer student to help with final details of new release, e. g. input, testing, documentation 10 April 2001 C++ Meta<Programming> 52

C++ Meta<Programming> Concepts and Results Walter E. Brown WB@fnal. gov f Fermi National Accelerator Laboratory C++ Meta<Programming>