C I R C U L A O

C I R C U L A Ç Ã O A circulação vertical faz-se por meio de ESCADAS, de RAMPAS e de ELEVADORES. V E R T I C A L DISCIPLINA DE DESENHO II ARQUITETURA E URBANISMO FAG

C V I R C U L A Ç Ã O E R T E S C A D A S DISCIPLINA DE DESENHO II ARQUITETURA E URBANISMO I C A L FAG

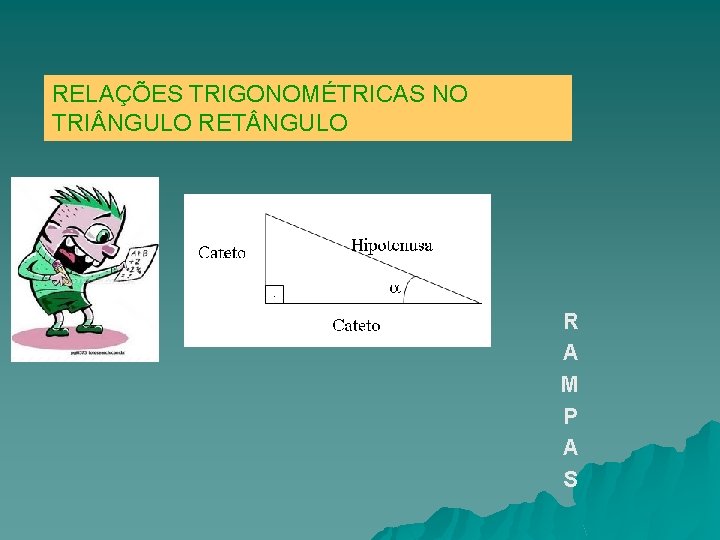
RELAÇÕES TRIGONOMÉTRICAS NO TRI NGULO RET NGULO R A M P A S

Rampas R A M P A S

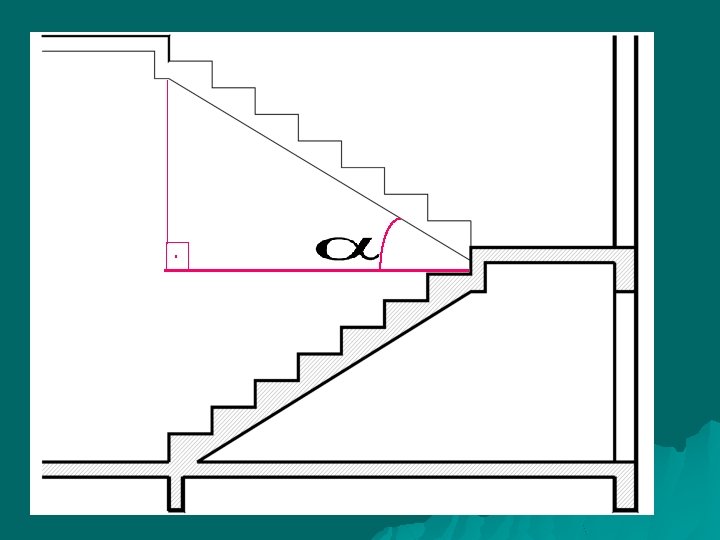
RAMPAS: A rampa é um plano inclinado que se utiliza para a circulação de pessoas, de cargas ou de veículos. Deve ser previsto patamar de descanso em condições semelhantes às da escada. As inclinações máximas das rampas são determinadas por normas, de acordo com o seu uso/destino na edificação. Para uso de pedestres a inclinação ideal é de 8 a 10%. Para uso de automóveis a inclinação máxima deve ser de 20%.

RAMPAS: Existe lei, que obriga, e normas técnicas que orientam, os projetos para a acessibilidade das pessoas portadoras de deficiências ou com mobilidade reduzida, mediante a supressão de barreiras e de obstáculos nas vias e espaços públicos, no mobiliário urbano, na construção e reforma de edifícios e nos meios de transporte e de comunicação.

DIMENSIONAMENTO: Rampas de lance reto: A inclinação das rampas deve ser calculada da seguinte forma: Se i=10%: Para cada 100 cm linear na horizontal, sobe-se 10 cm em altura: Neste caso, para subir 3 m de altura (h=3, 00) são necessários 30 m de rampa, pois 3 m= 10% de 30 m.

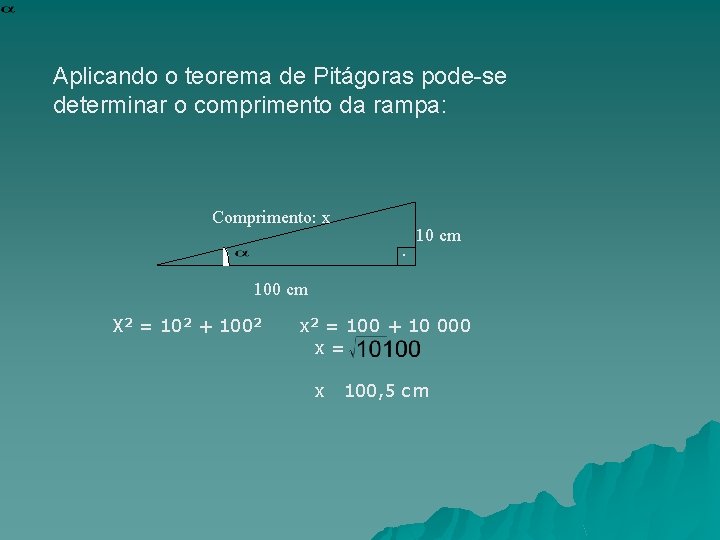
Aplicando o teorema de Pitágoras pode-se determinar o comprimento da rampa: Comprimento: x 10 cm. 100 cm X 2 = 102 + 1002 x 2 = 100 + 10 000 x= x 100, 5 cm

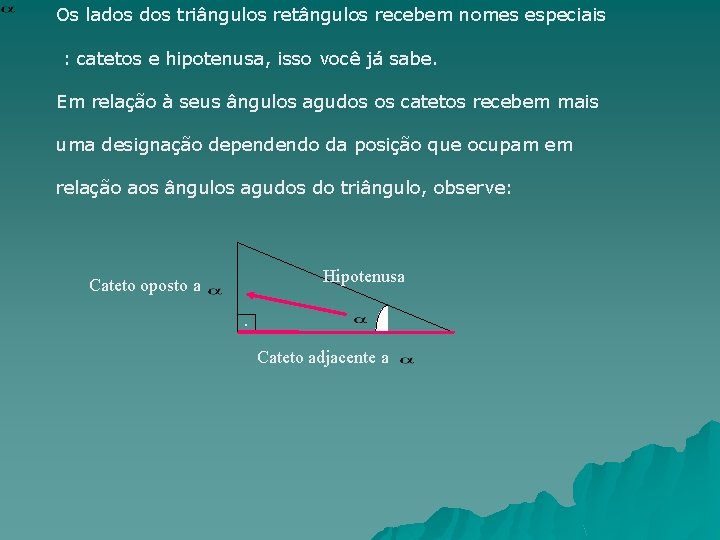
Os lados triângulos retângulos recebem nomes especiais : catetos e hipotenusa, isso você já sabe. Em relação à seus ângulos agudos os catetos recebem mais uma designação dependendo da posição que ocupam em relação aos ângulos agudos do triângulo, observe: Hipotenusa Cateto oposto a. Cateto adjacente a

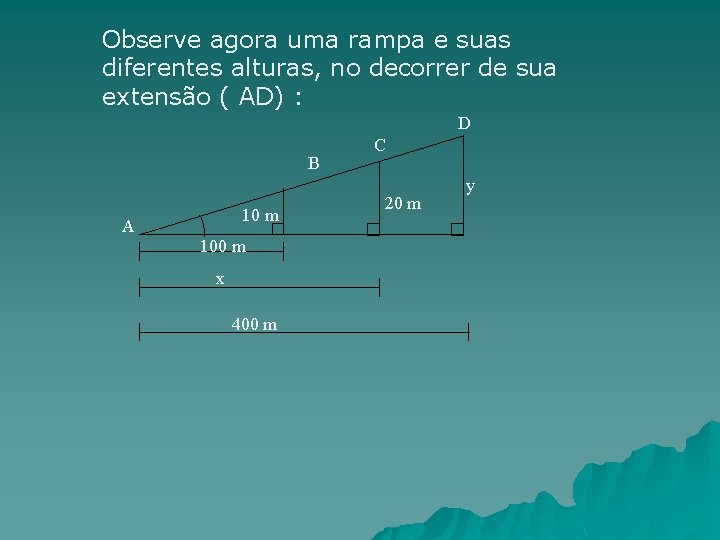
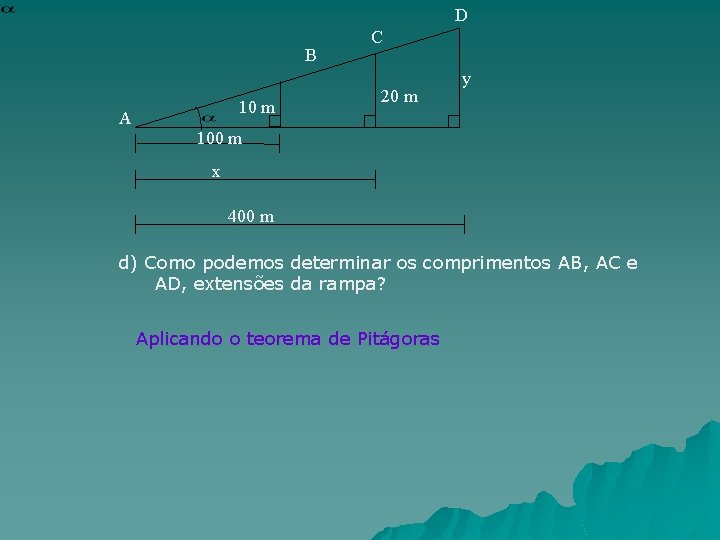
Observe agora uma rampa e suas diferentes alturas, no decorrer de sua extensão ( AD) : D B 10 m A 100 m x 400 m C 20 m y

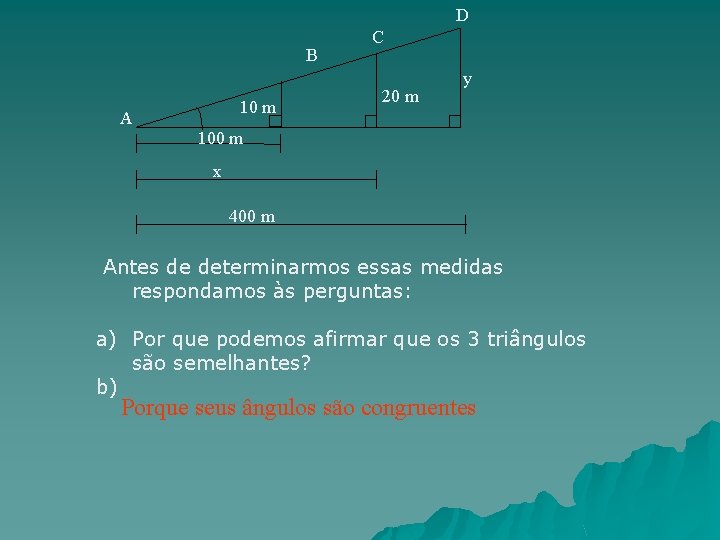
D B 10 m A C 20 m y 100 m x 400 m Antes de determinarmos essas medidas respondamos às perguntas: a) Por que podemos afirmar que os 3 triângulos são semelhantes? b) Porque seus ângulos são congruentes

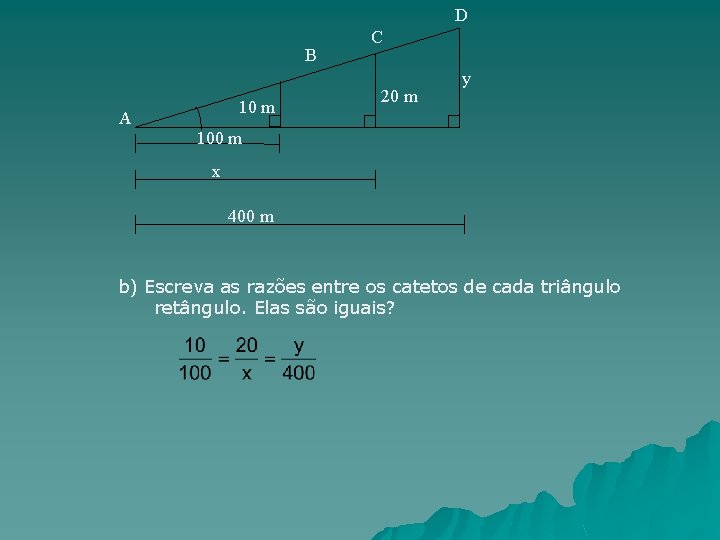
D B 10 m A C 20 m y 100 m x 400 m b) Escreva as razões entre os catetos de cada triângulo retângulo. Elas são iguais?

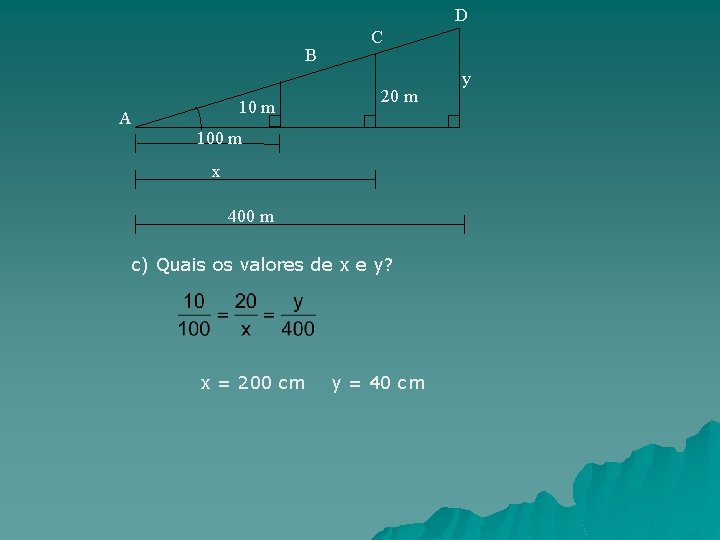
D B 10 m A C 20 m 100 m x 400 m c) Quais os valores de x e y? x = 200 cm y = 40 cm y

D B 10 m A C 20 m y 100 m x 400 m d) Como podemos determinar os comprimentos AB, AC e AD, extensões da rampa? Aplicando o teorema de Pitágoras

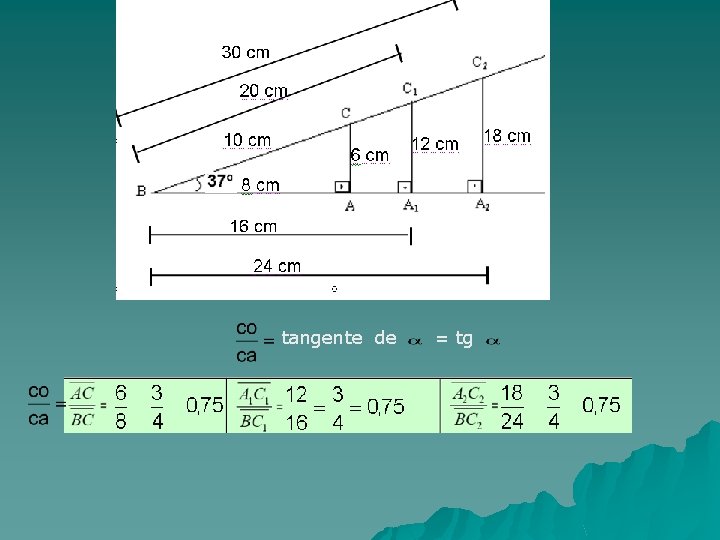
tangente de = tg

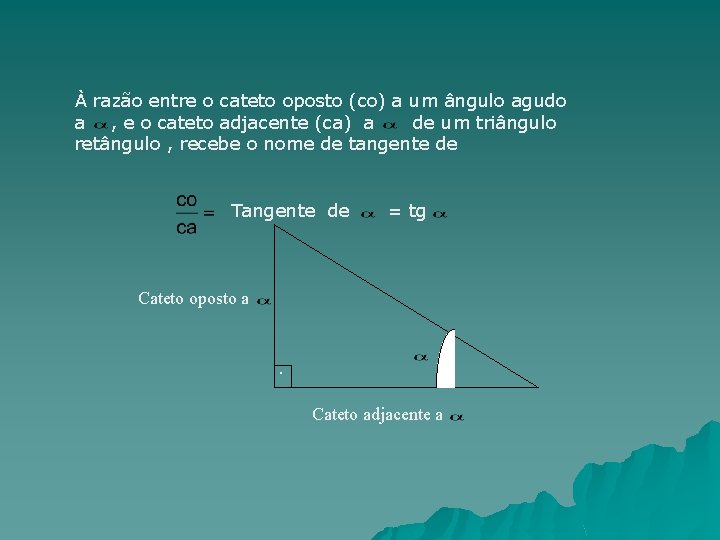
À razão entre o cateto oposto (co) a um ângulo agudo a , e o cateto adjacente (ca) a de um triângulo retângulo , recebe o nome de tangente de Tangente de = tg Cateto oposto a . Cateto adjacente a

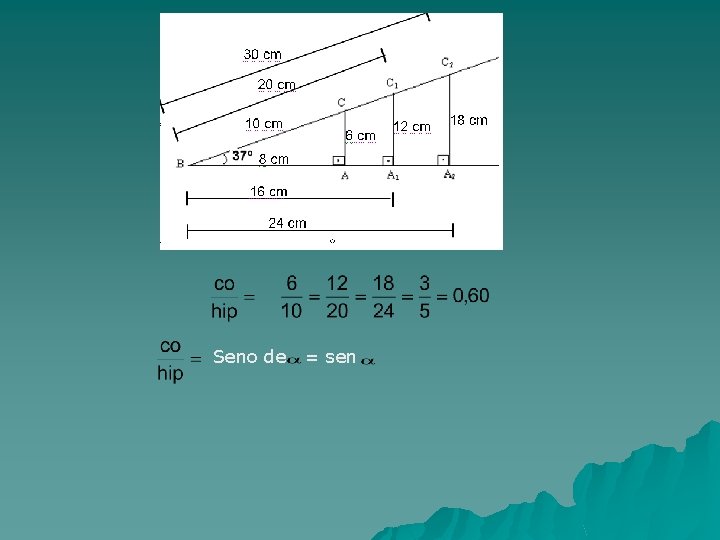
Seno de = sen

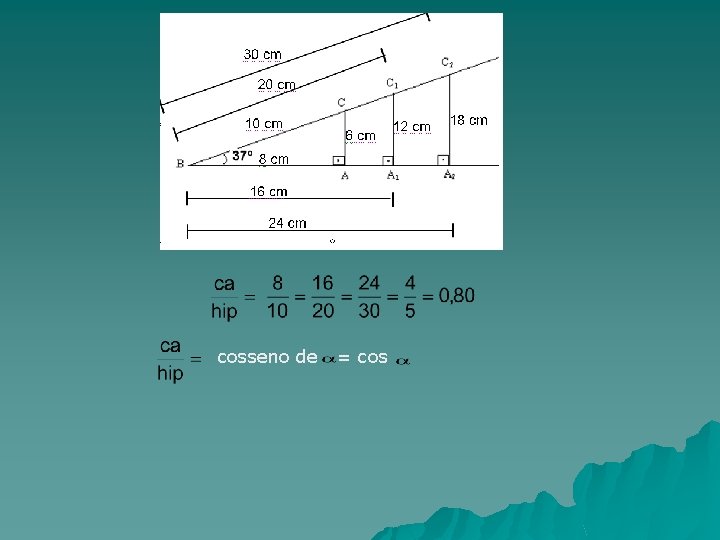
cosseno de = cos

Vamos pensar. . .

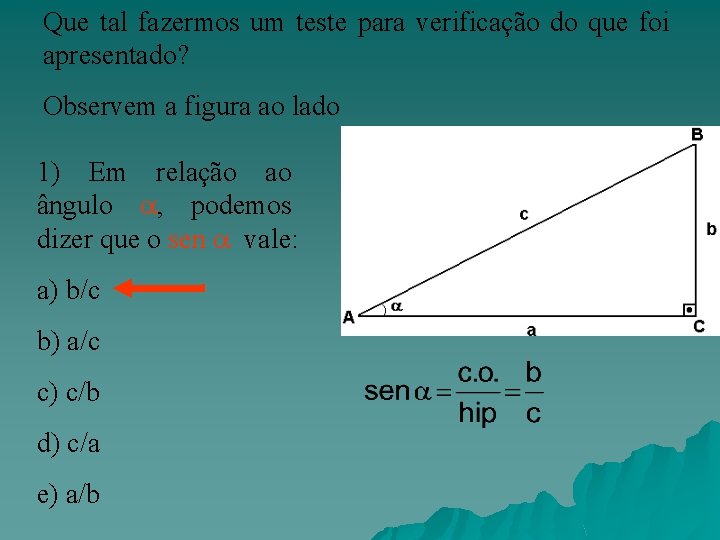
Que tal fazermos um teste para verificação do que foi apresentado? Observem a figura ao lado 1) Em relação ao ângulo , podemos dizer que o sen vale: a) b/c b) a/c c) c/b d) c/a e) a/b

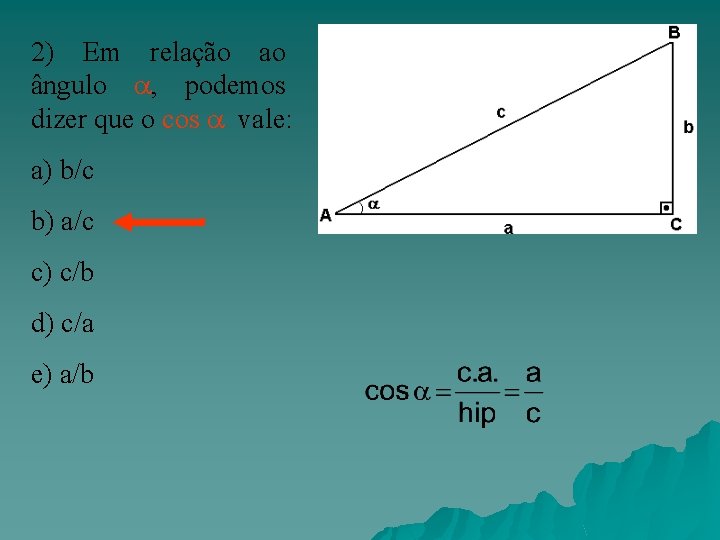
2) Em relação ao ângulo , podemos dizer que o cos vale: a) b/c b) a/c c) c/b d) c/a e) a/b

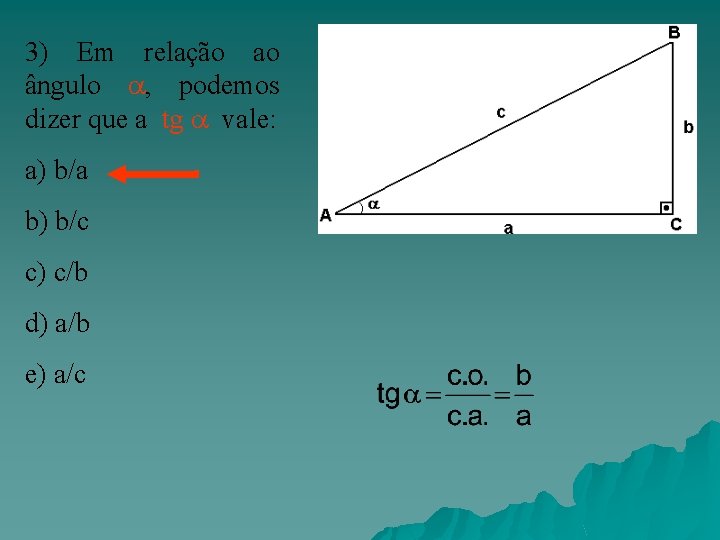
3) Em relação ao ângulo , podemos dizer que a tg vale: a) b/a b) b/c c) c/b d) a/b e) a/c

Trigonometria Algumas Aplicações

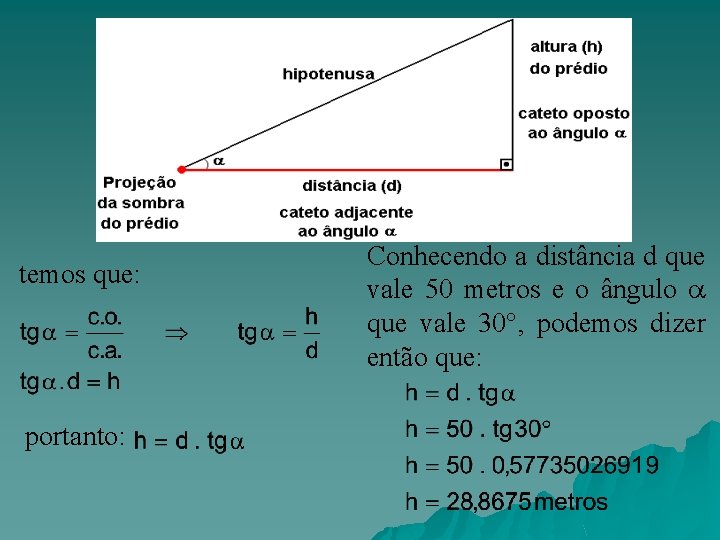
Parte Prática O exemplo clássico da Sombra Para que possamos medir (aproximadamente) a altura de um prédio, sem a necessidade de subir ao terraço, ou utilizar equipamentos sofisticados, seria necessário somente 2 elementos. São eles: uma distância um ângulo Observe a seguir. . .

temos que: portanto: Conhecendo a distância d que vale 50 metros e o ângulo que vale 30°, podemos dizer então que: