C E 33 Conic Sections in General Form

General Form of a Conic Equation We sometimes see conic equations written in General

A conic equation written in General Form doesn’t have to have all SIX terms!

So, it’s a conic equation if. . . • the highest degree (power) of

The values of the coefficients in the conic equation determine the TYPE of conic.

Circles. . . where A & C have the SAME SIGN and they have

Ellipses. . . where A & C have the SAME SIGN but DIFFERENT VALUES

Hyperbola. . . where A & C have DIFFERENT signs. NOTE: There is no

Parabola. . . A Parabola can be oriented 2 different ways: A parabola is

Parabola …Vertical The following equations all represent vertical parabolas in general form; they all

Parabola …Horizontal The following equations all represent horizontal parabolas in general form, they all

Summary. . . General Form of a Conic Equation: where A, B, C, D,

Practice. . . Identify each of the following equations as a(n): (a) ellipse (b)

Answers. . . (a) ellipse (b) circle (c) hyperbola (d) parabola (e) not a

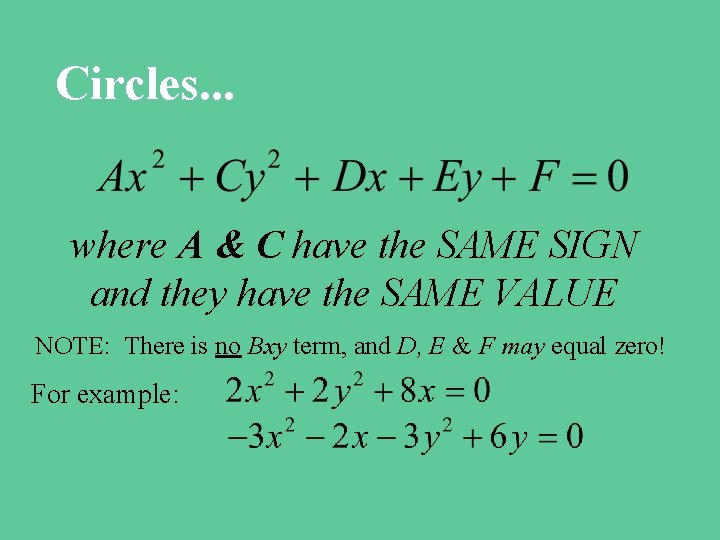
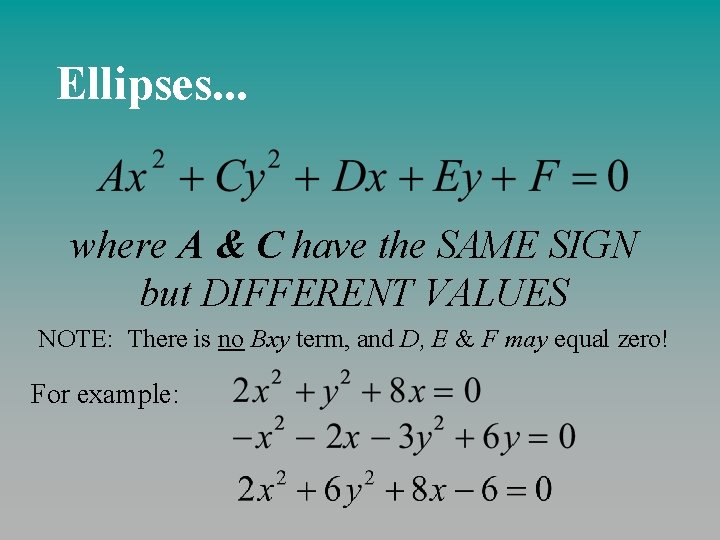
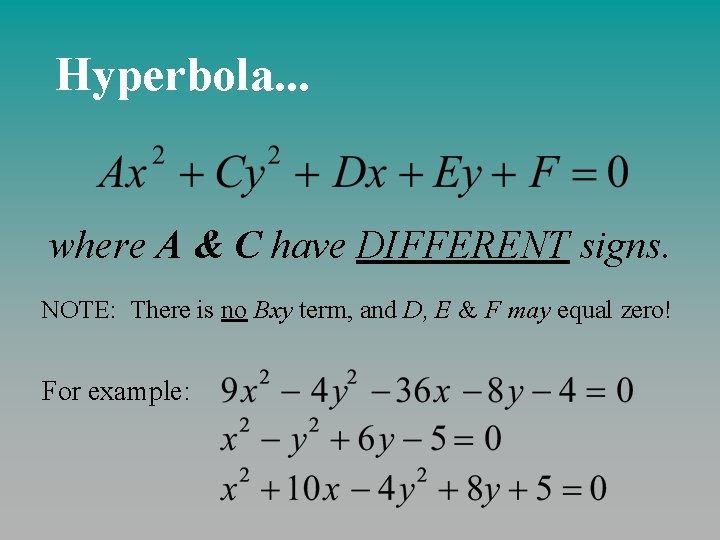
Slides: 14

Download presentation

C E 33. Conic Sections in General Form H P

General Form of a Conic Equation We sometimes see conic equations written in General Form: where A, B, C, D, E and F are integers and A, B and C are NOT ALL equal to zero.

A conic equation written in General Form doesn’t have to have all SIX terms! Several of the coefficients A, B, C, D, E and F can equal zero, as long as A, B and C don’t ALL equal zero. If A, B and C all equal zero, what kind of equation do you have? . . . T H I N K. . . Linear!

So, it’s a conic equation if. . . • the highest degree (power) of x and/or y is 2 (at least ONE has to be squared) • the other terms are either linear, constant, or the product of x and y • there are no variable terms with rational exponents (i. e. no radical expressions) or terms with negative exponents (i. e. no rational expressions)

The values of the coefficients in the conic equation determine the TYPE of conic. What values form a circle? What values form an Ellipse? What values form a Hyperbola? What values form a Parabola?

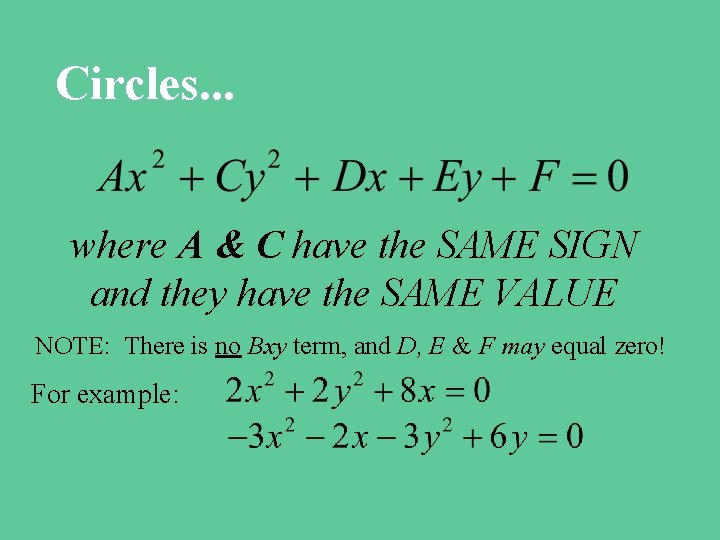
Circles. . . where A & C have the SAME SIGN and they have the SAME VALUE NOTE: There is no Bxy term, and D, E & F may equal zero! For example:

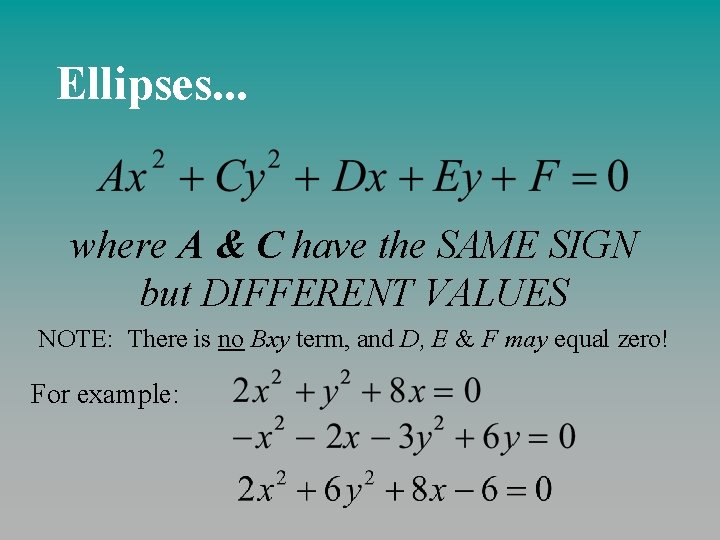
Ellipses. . . where A & C have the SAME SIGN but DIFFERENT VALUES NOTE: There is no Bxy term, and D, E & F may equal zero! For example:

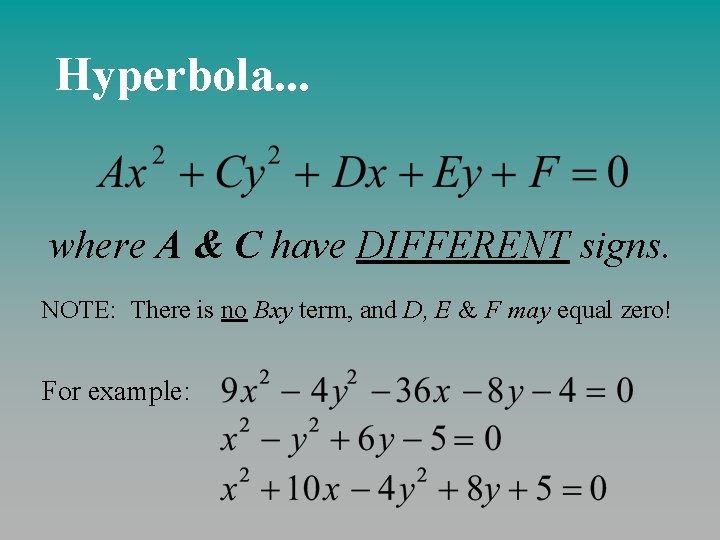
Hyperbola. . . where A & C have DIFFERENT signs. NOTE: There is no Bxy term, and D, E & F may equal zero! For example:

Parabola. . . A Parabola can be oriented 2 different ways: A parabola is vertical if the equation has an x squared term AND a linear y term; it may or may not have a linear x term & constant: A parabola is horizontal if the equation has a y squared term AND a linear x term; it may or may not have a linear y term & constant:

Parabola …Vertical The following equations all represent vertical parabolas in general form; they all have a squared x term and a linear y term:

Parabola …Horizontal The following equations all represent horizontal parabolas in general form, they all have a squared y term and a linear x term:

Summary. . . General Form of a Conic Equation: where A, B, C, D, E and F are integers and A, B and C are NOT ALL equal to zero. Identifying a Conic Equation:

Practice. . . Identify each of the following equations as a(n): (a) ellipse (b) circle (d) parabola (e) not a conic (c) hyperbola See if you can rewrite each equation into its Graphing Form!

Answers. . . (a) ellipse (b) circle (c) hyperbola (d) parabola (e) not a conic