C Classes and Data Structures Recursion 1 Recursive

















































- Slides: 96

C++ Classes and Data Structures Recursion 1

Recursive Functions • Recursive functions are functions that call themselves • Data structures, especially linked implementations of binary trees, sometimes use recursive functions 2

Example: Factorial Function • The factorial function is often written as a recursive function • The factorial of a positive integer is the product of all positive integers less than or equal to the number 5 factorial is written 5! 5! = 5 * 4 * 3 * 2 * 1 = 120 3! = 3 * 2 * 1 = 6 0! is defined to be 1 3

Factorial Function 1 2 3 4 5 6 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 4

Factorial Function 1 2 3 4 5 6 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } The recursive function call 5

What Happens When a Function Calls Itself? • When a function calls itself, it is not actually executing itself again • Instead, another function is made which is identical • Then, that function is called from the recursive function call • This will be illustrated in the slides that follow… 6

Recursive Process x = factorial( 4 ); A function call that should produce 24 as a result and assign it to x. 7

Recursive Process (cont. ) x = factorial( 4 ); 4 is passed into num int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 8

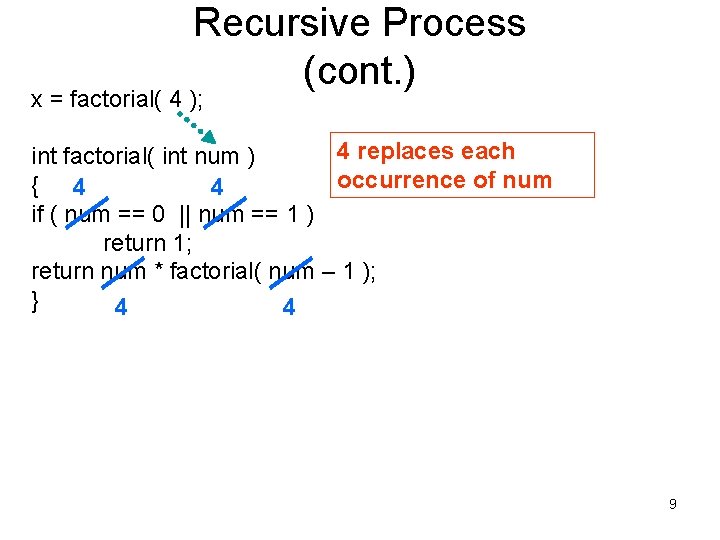
Recursive Process (cont. ) x = factorial( 4 ); 4 replaces each int factorial( int num ) occurrence of num { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 4 4 9

Recursive Process (cont. ) x = factorial( 4 ); int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 4 4 10

Recursive Process (cont. ) x = factorial( 4 ); int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 4 4 11

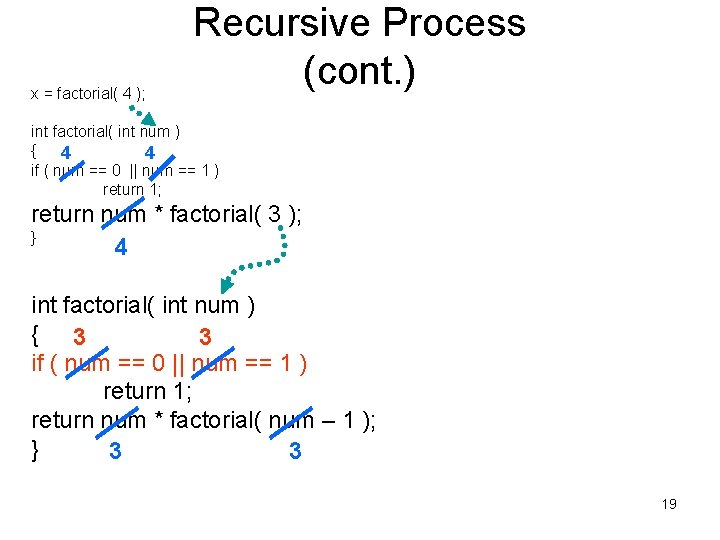
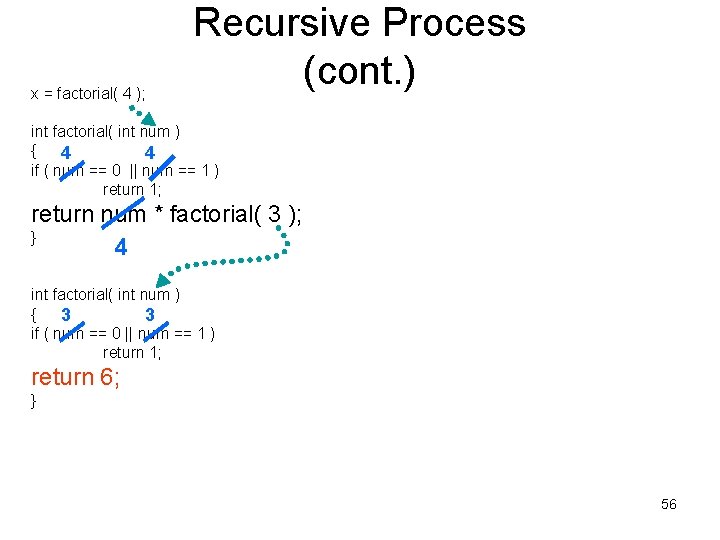
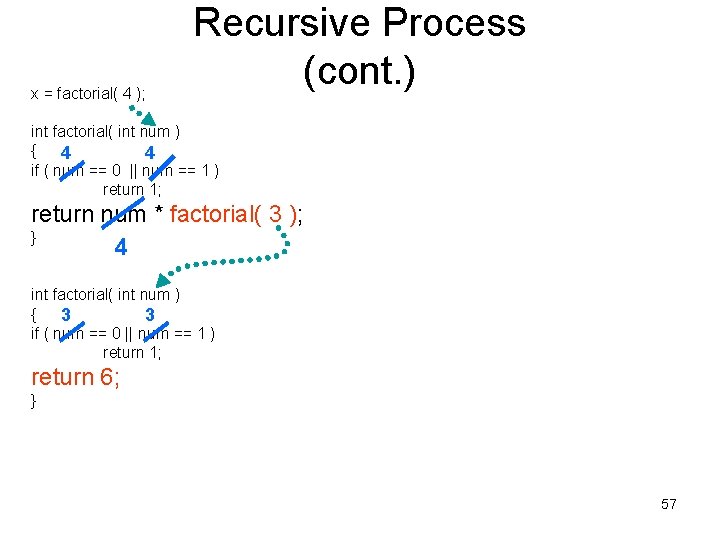
Recursive Process (cont. ) x = factorial( 4 ); int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 12

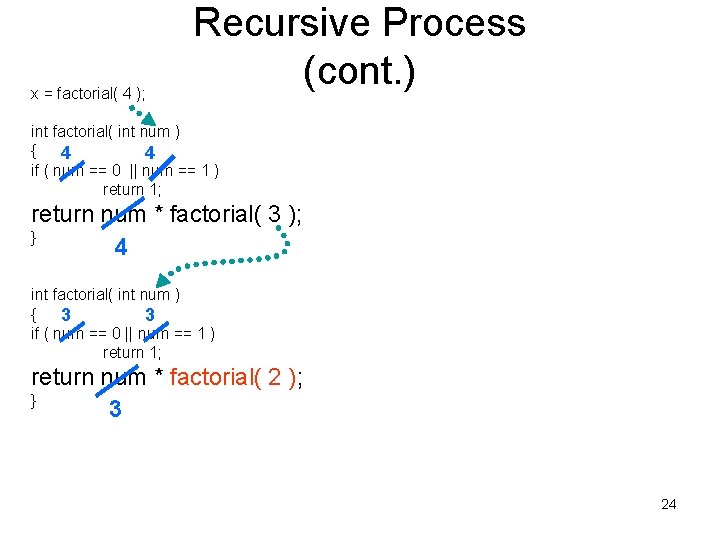
Recursive Process (cont. ) x = factorial( 4 ); int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 13

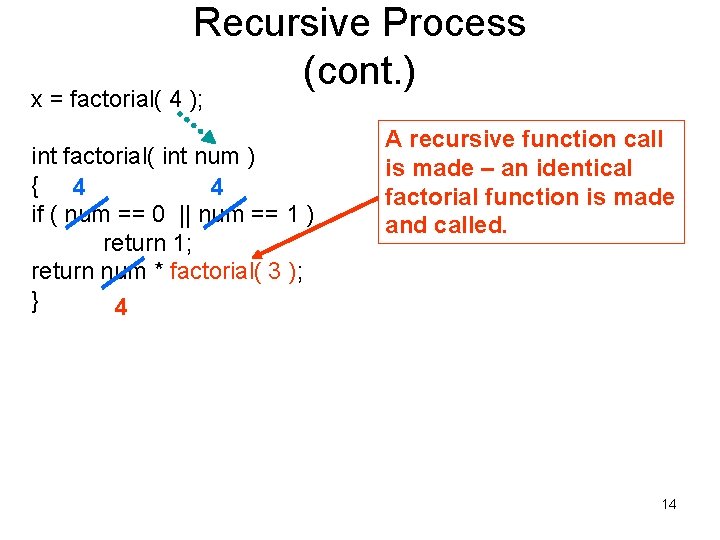
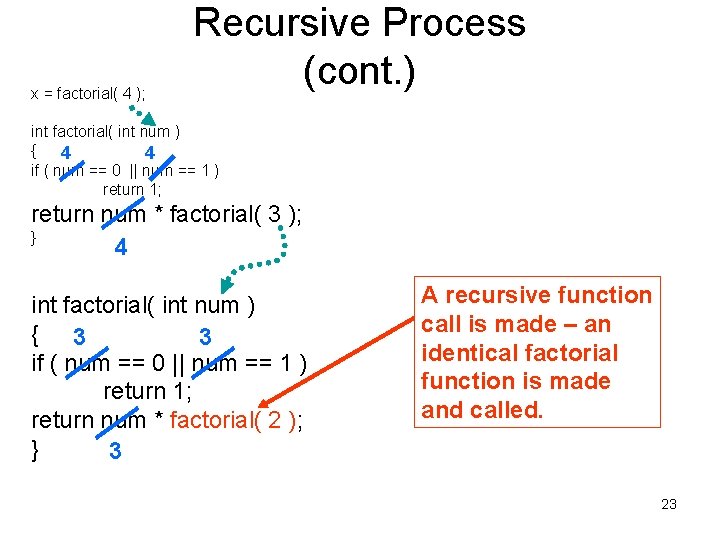
Recursive Process (cont. ) x = factorial( 4 ); int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 A recursive function call is made – an identical factorial function is made and called. 14

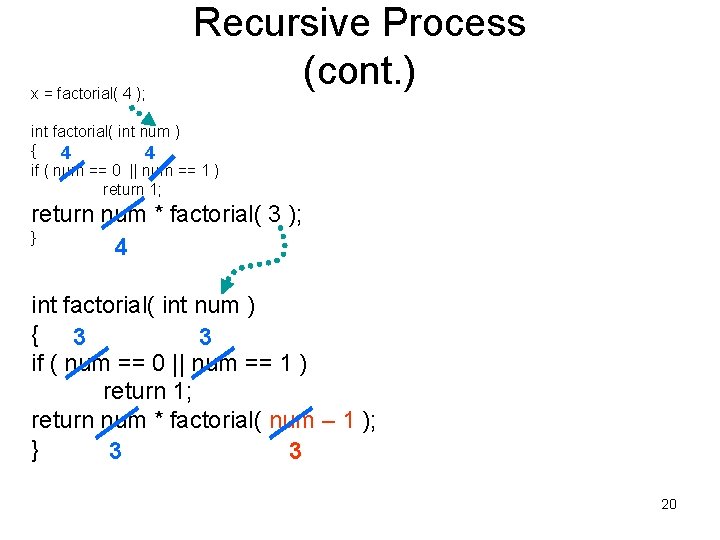
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 15

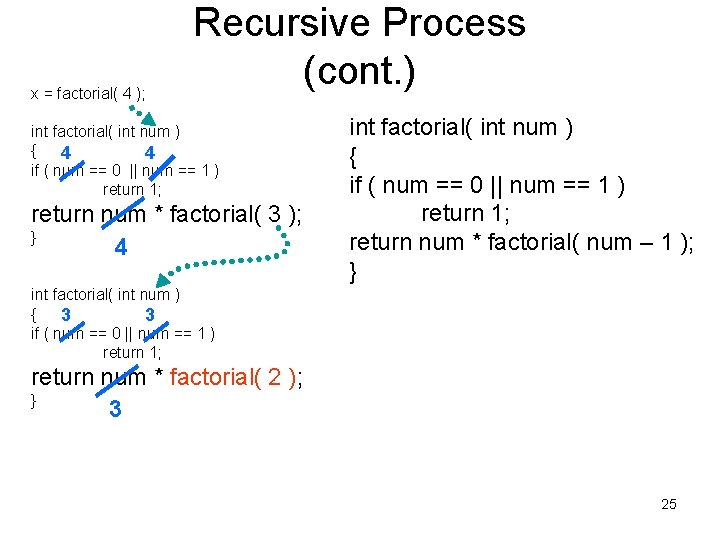
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 16

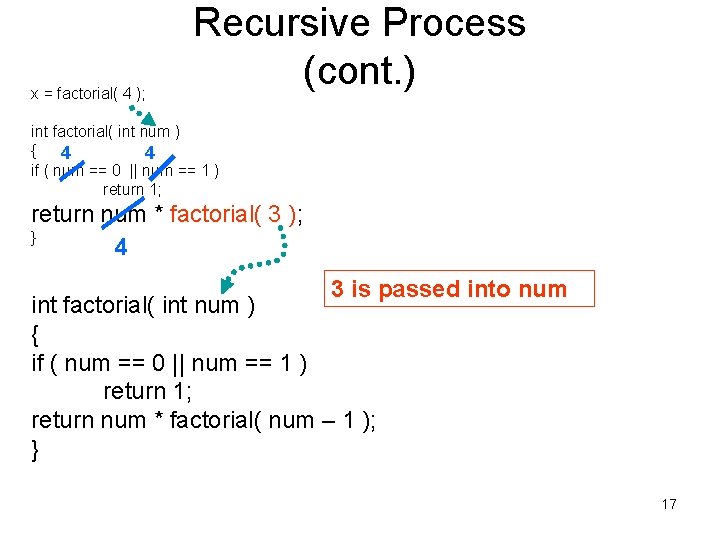
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 3 is passed into num int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 17

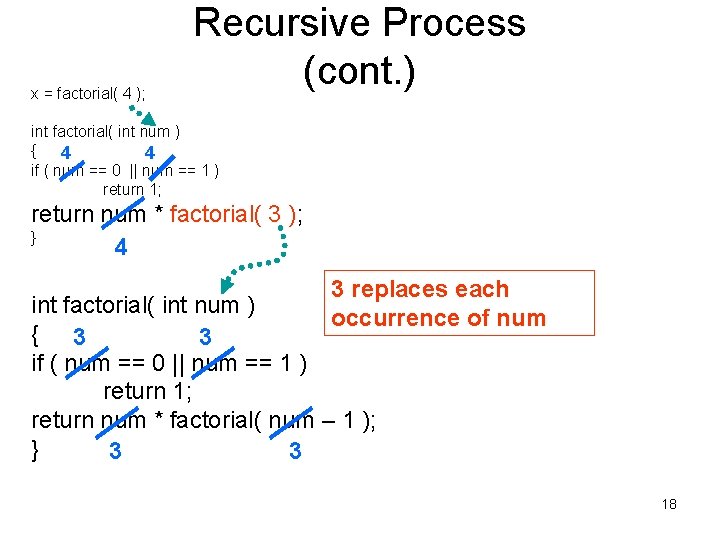
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 3 replaces each occurrence of num int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 3 3 18

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 3 3 19

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 3 3 20

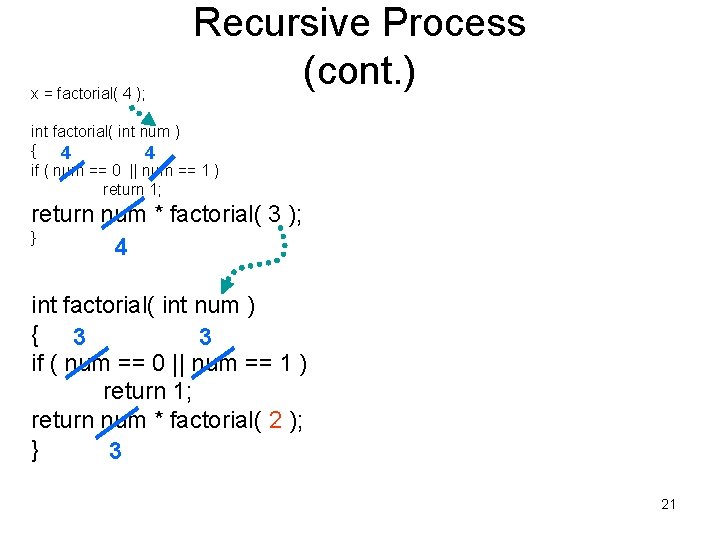
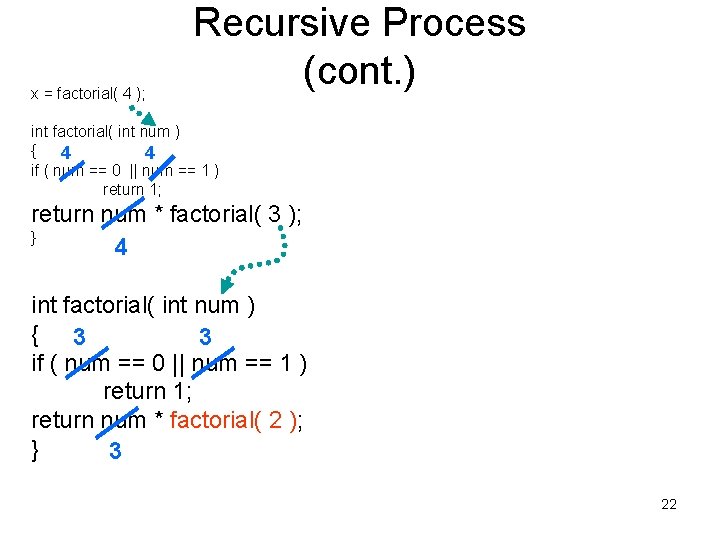
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 21

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 22

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 A recursive function call is made – an identical factorial function is made and called. 23

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 24

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 25

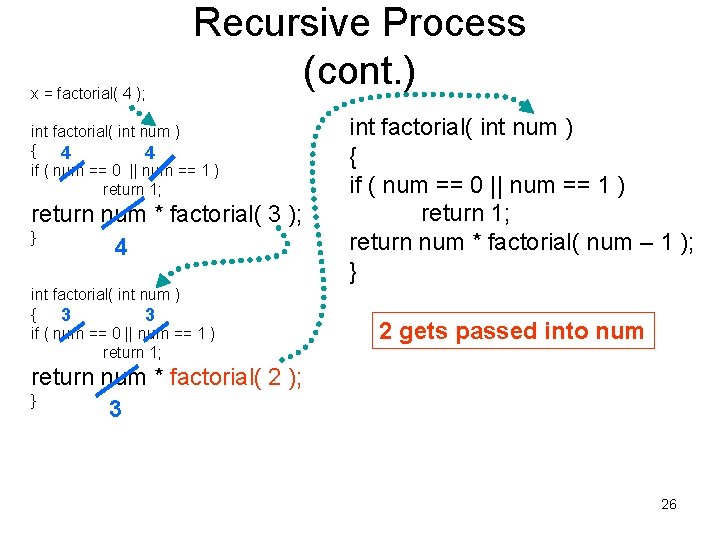
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 2 gets passed into num return num * factorial( 2 ); } 3 26

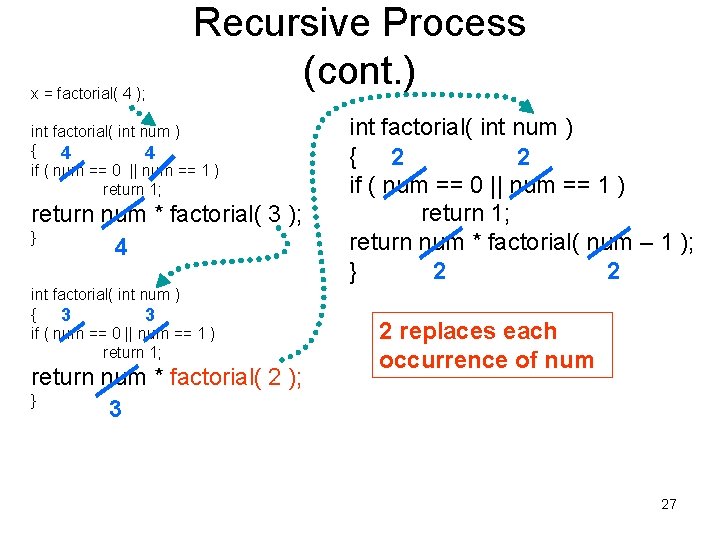
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 2 2 2 replaces each occurrence of num 27

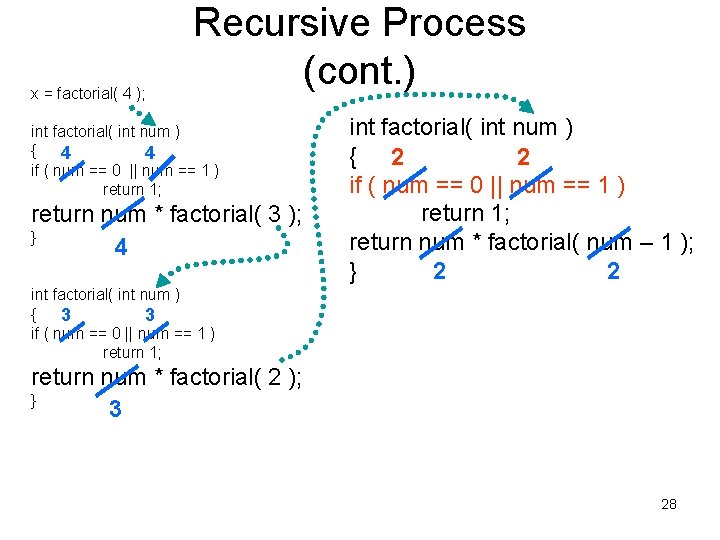
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 2 2 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 28

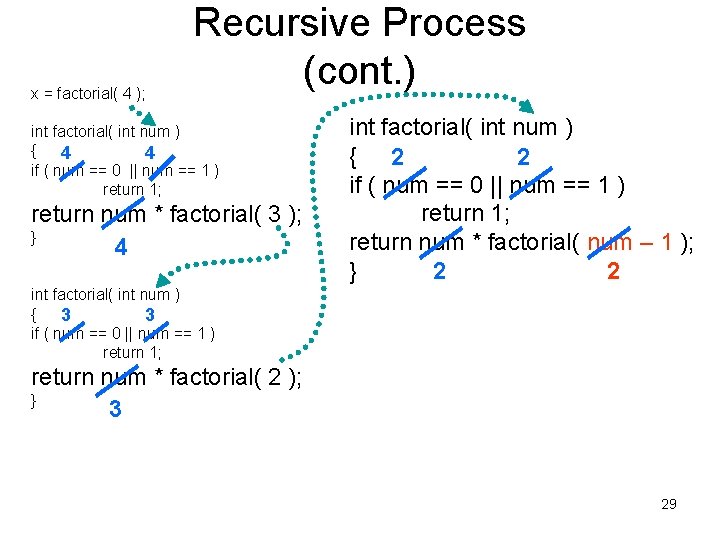
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 2 2 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 29

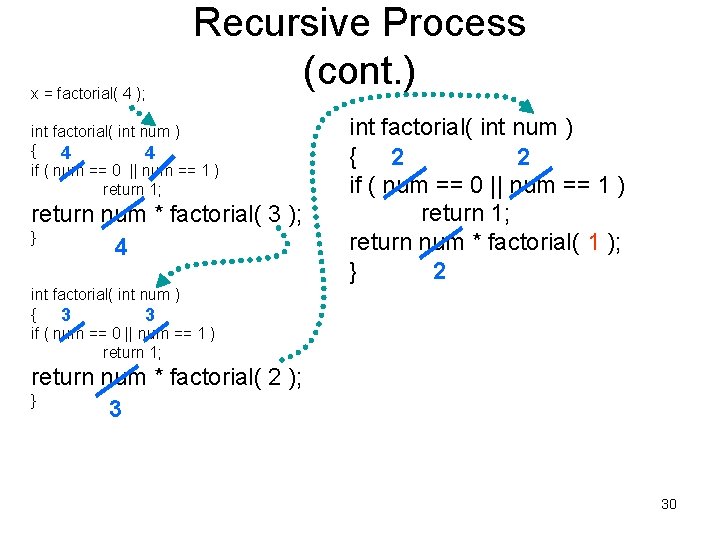
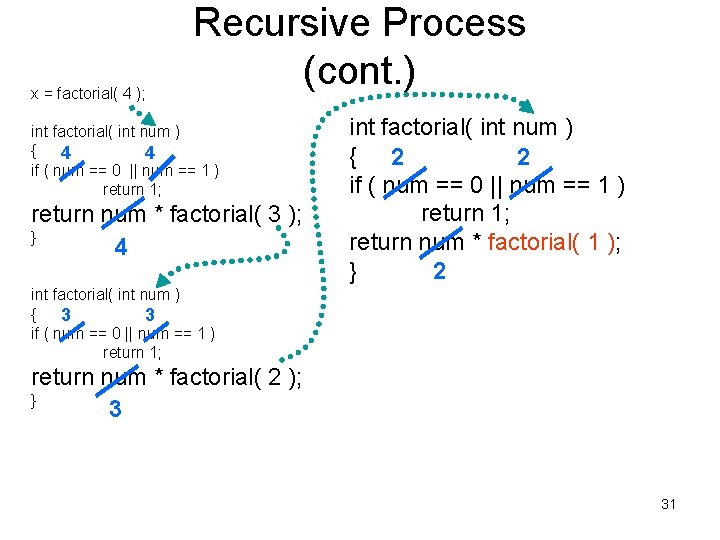
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 30

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 31

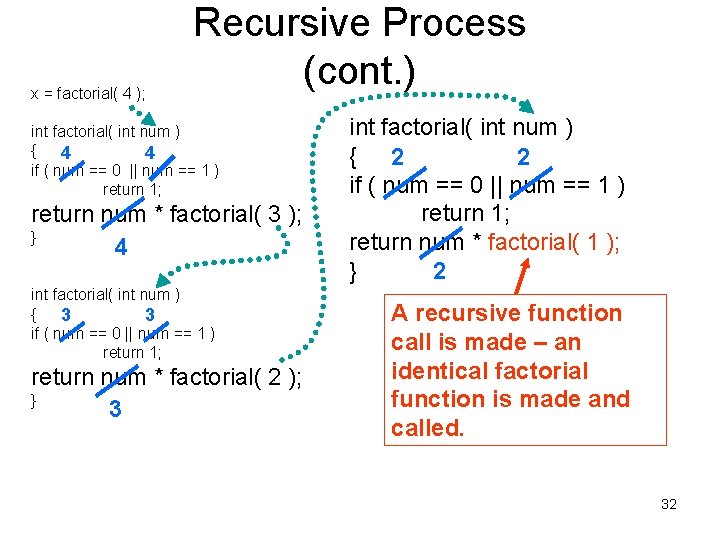
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 A recursive function call is made – an identical factorial function is made and called. 32

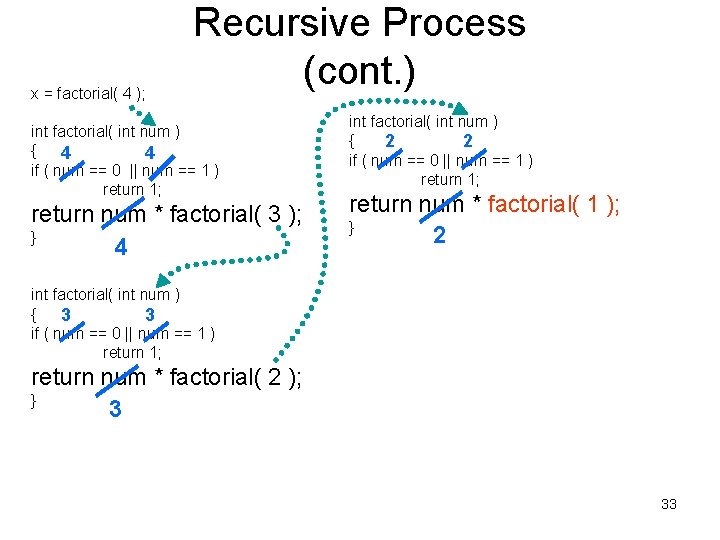
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 33

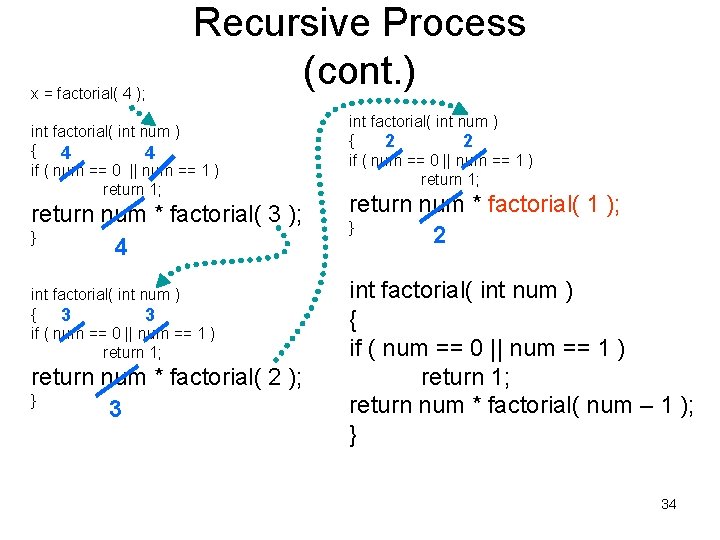
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 34

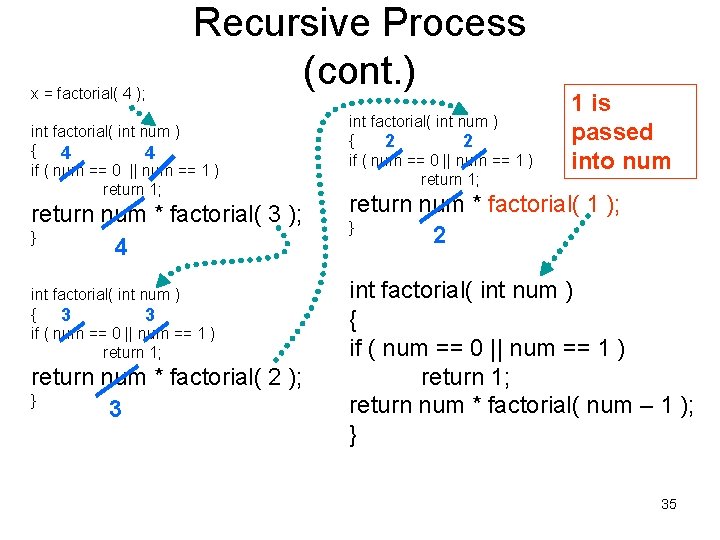
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; 1 is passed into num return num * factorial( 1 ); } 2 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 35

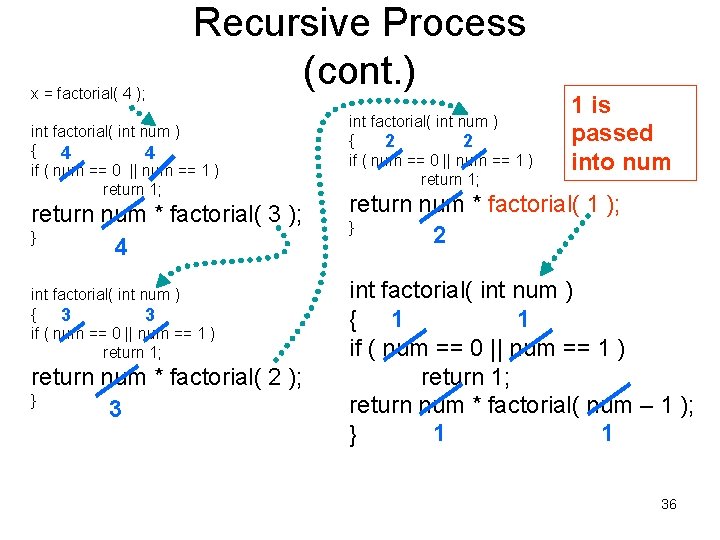
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; 1 is passed into num return num * factorial( 1 ); } 2 int factorial( int num ) 1 { 1 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); 1 1 } 36

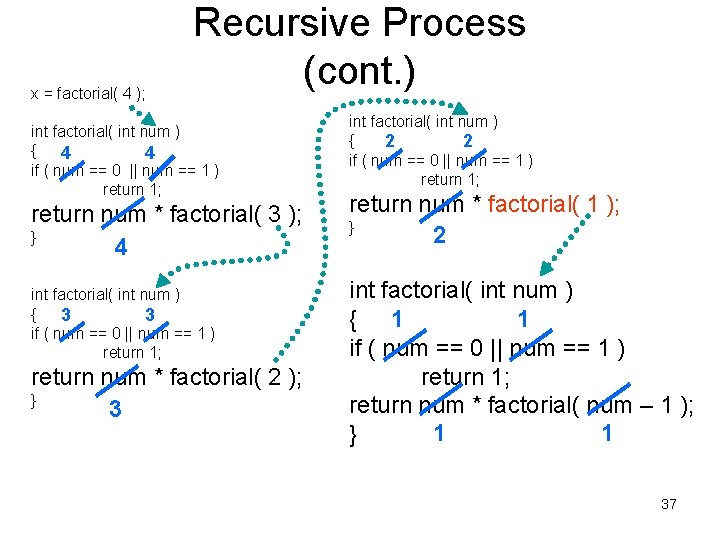
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 int factorial( int num ) 1 { 1 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); 1 1 } 37

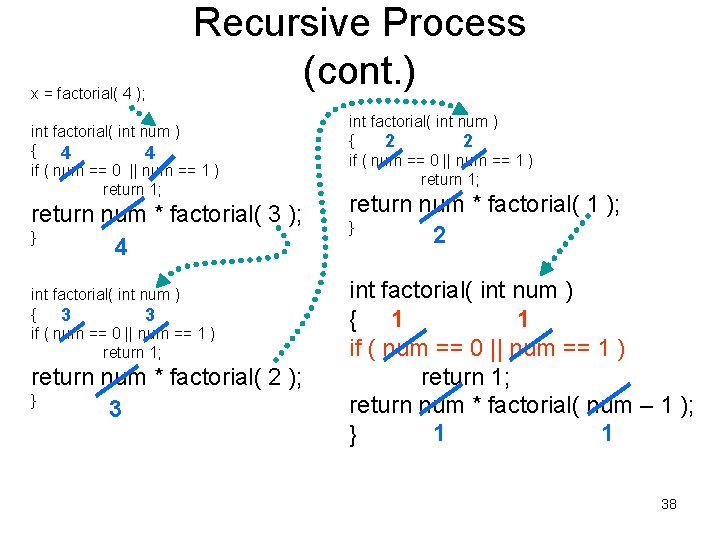
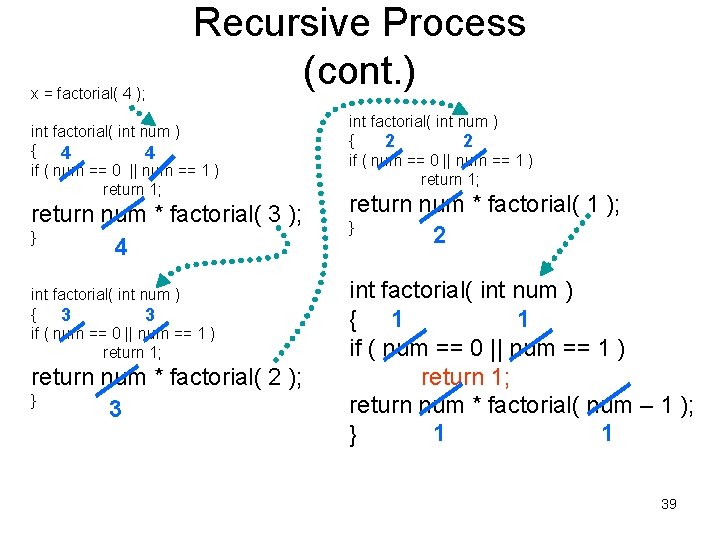
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 int factorial( int num ) 1 { 1 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); 1 1 } 38

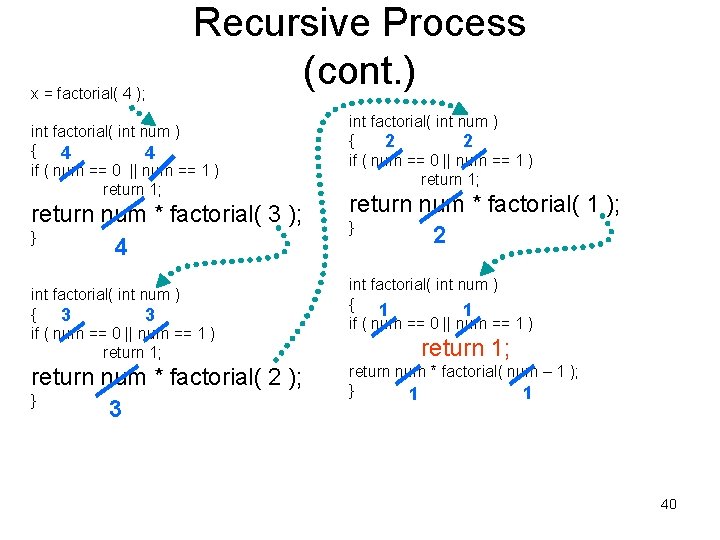
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 int factorial( int num ) 1 { 1 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); 1 1 } 39

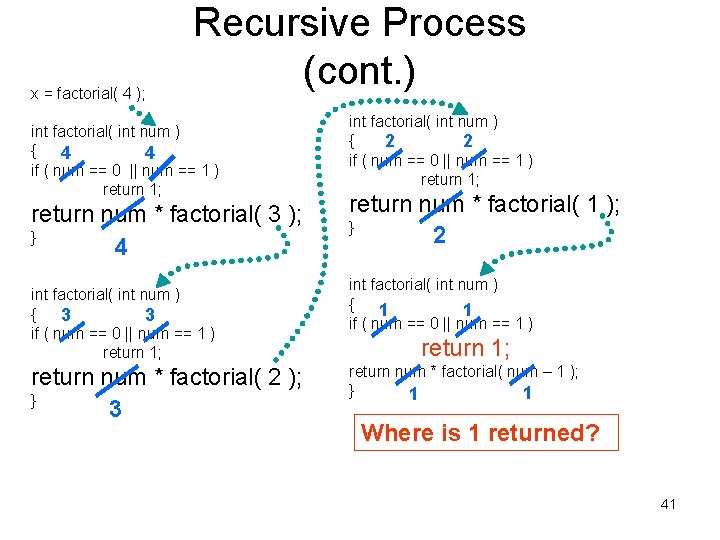
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 int factorial( int num ) { 1 1 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 1 1 40

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 int factorial( int num ) { 1 1 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 1 1 Where is 1 returned? 41

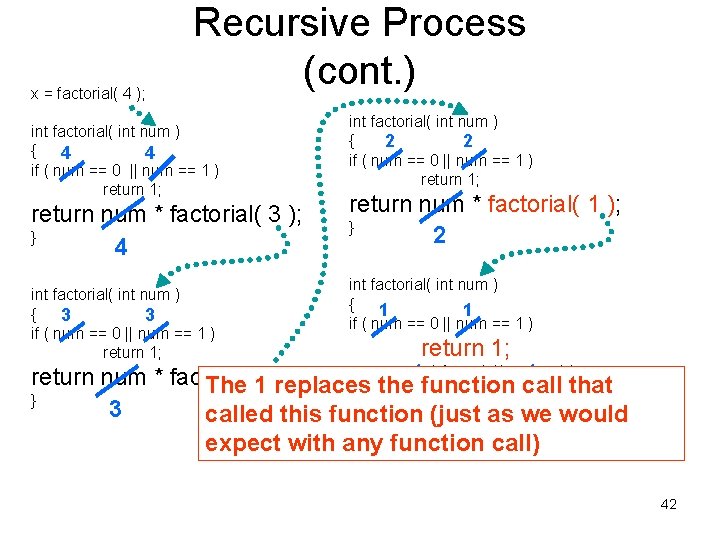
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 int factorial( int num ) { 1 1 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); return num * factorial( 2 ); The 1 replaces that } the 1 function call 1 } 3 called this function (just as we would expect with any function call) 42

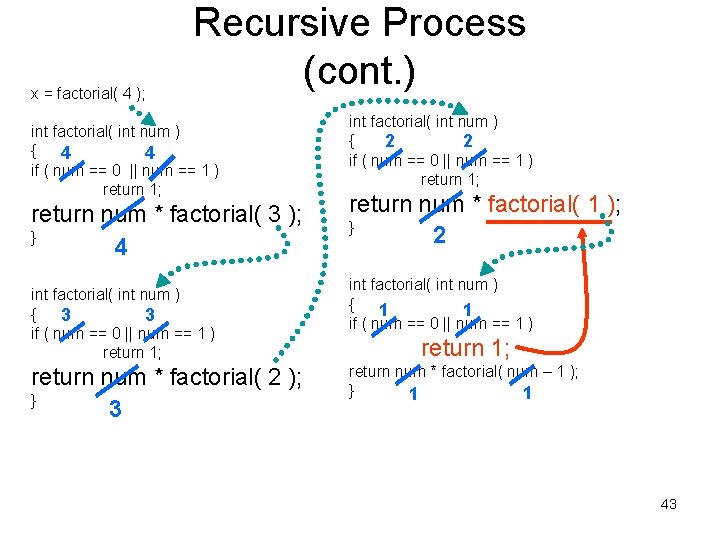
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * factorial( 1 ); } 2 int factorial( int num ) { 1 1 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 1 1 43

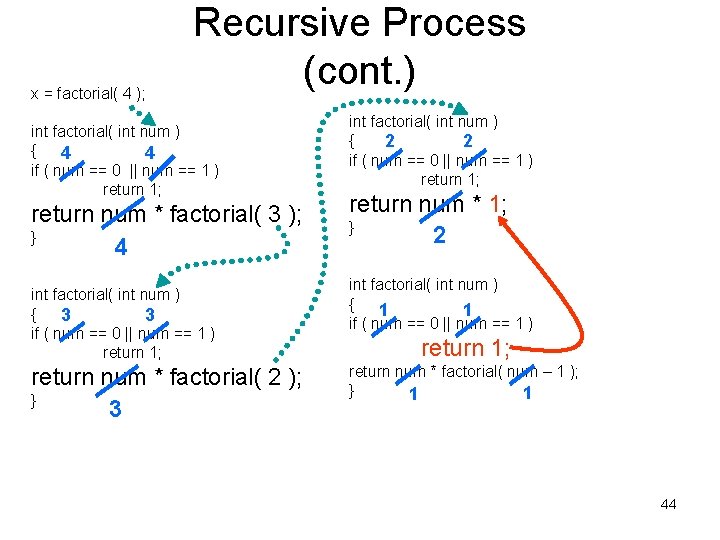
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * 1; } 2 int factorial( int num ) { 1 1 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 1 1 44

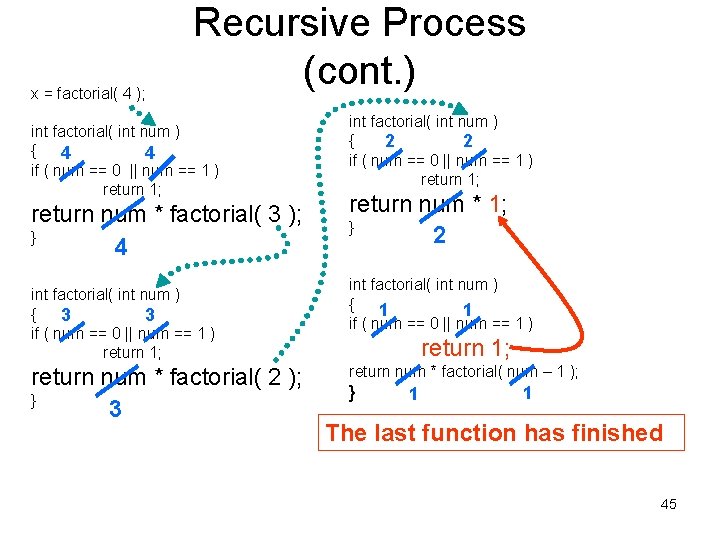
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * 1; } 2 int factorial( int num ) { 1 1 if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } 1 1 The last function has finished 45

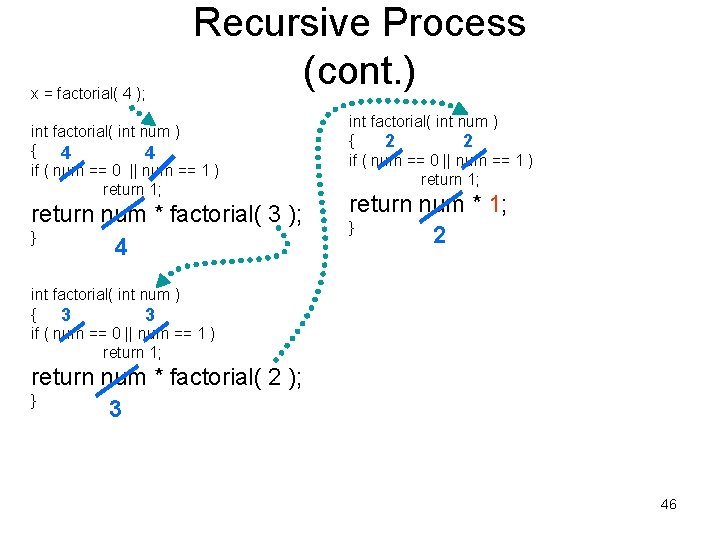
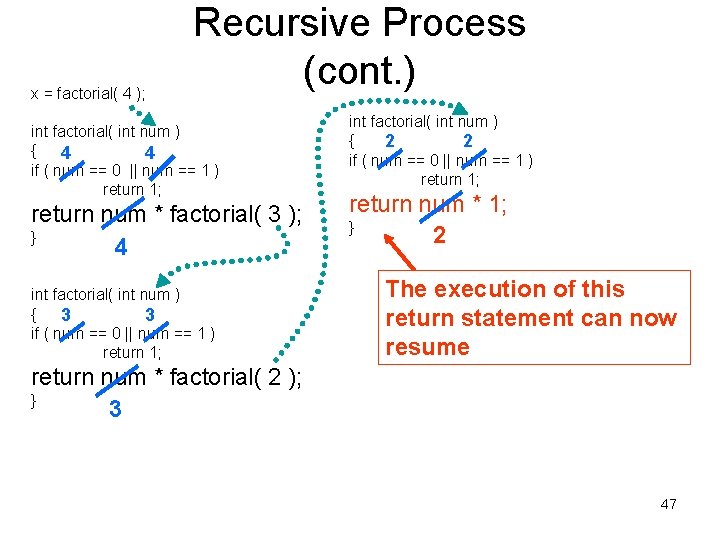
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * 1; } 2 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 46

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return num * 1; } 2 The execution of this return statement can now resume return num * factorial( 2 ); } 3 47

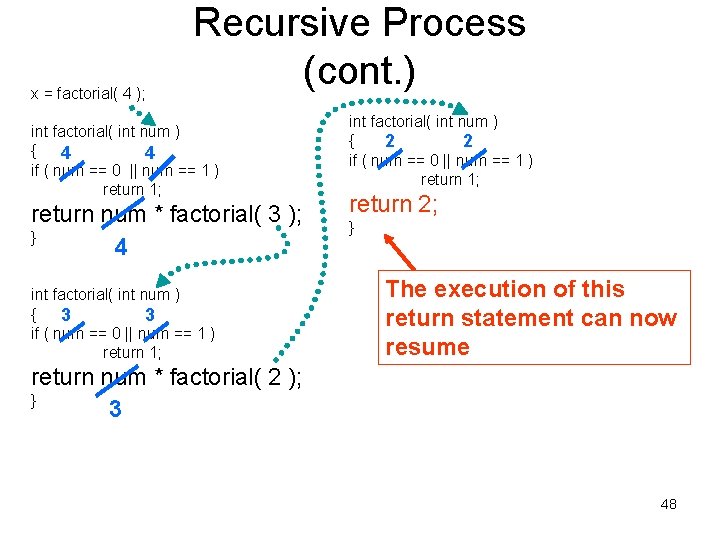
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return 2; } The execution of this return statement can now resume return num * factorial( 2 ); } 3 48

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return 2; } It now returns 2 back to the function call that called this function. return num * factorial( 2 ); } 3 49

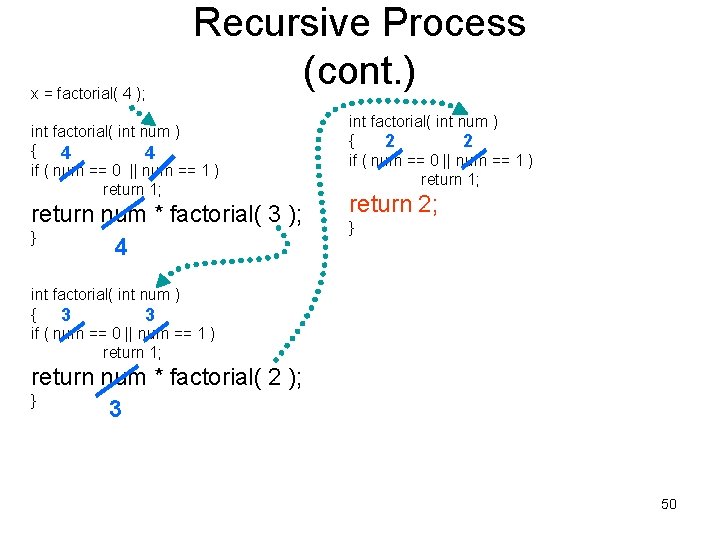
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return 2; } int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 50

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return 2; } int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 51

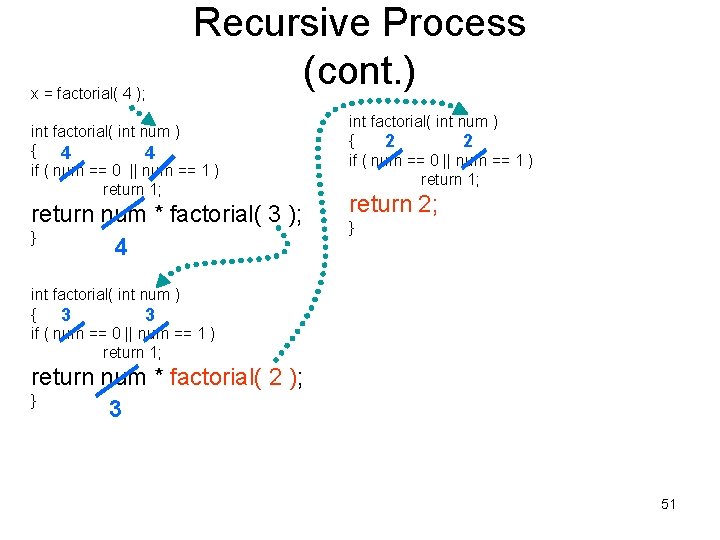
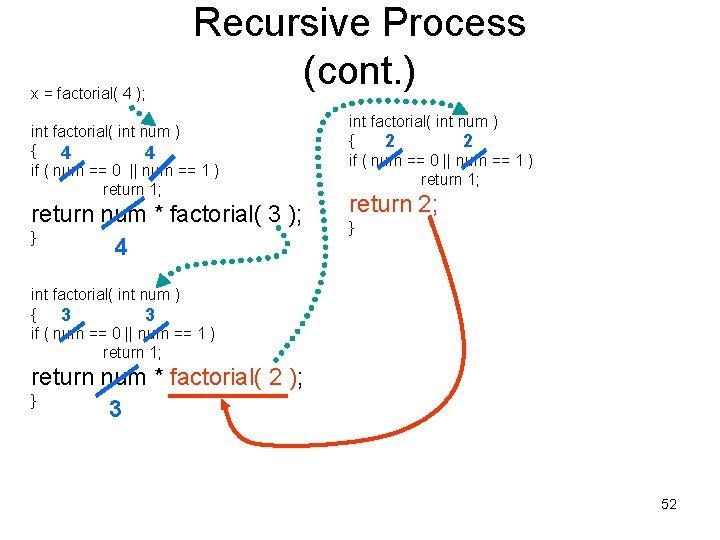
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return 2; } int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * factorial( 2 ); } 3 52

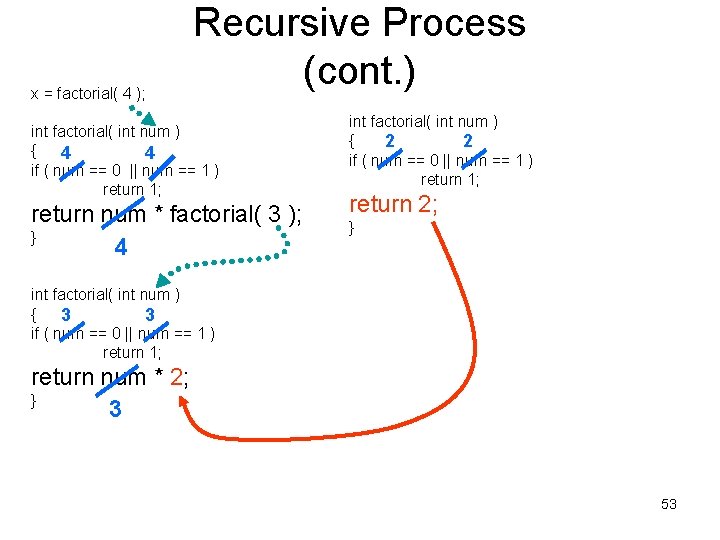
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 2 2 if ( num == 0 || num == 1 ) return 1; return 2; } int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * 2; } 3 53

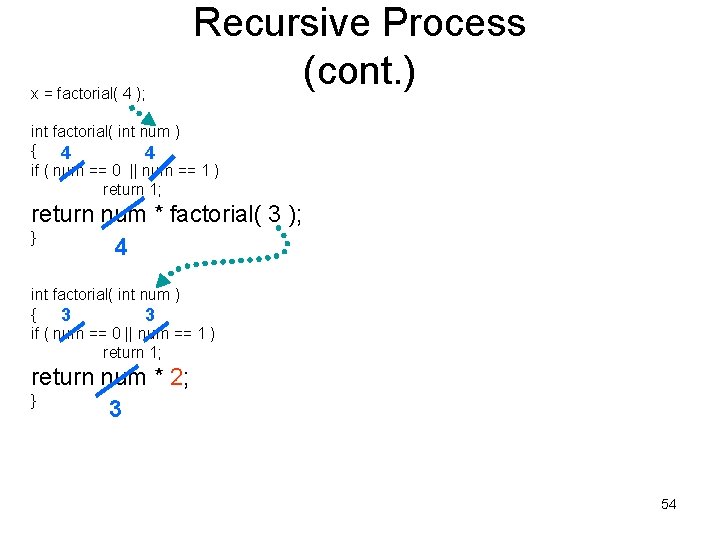
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * 2; } 3 54

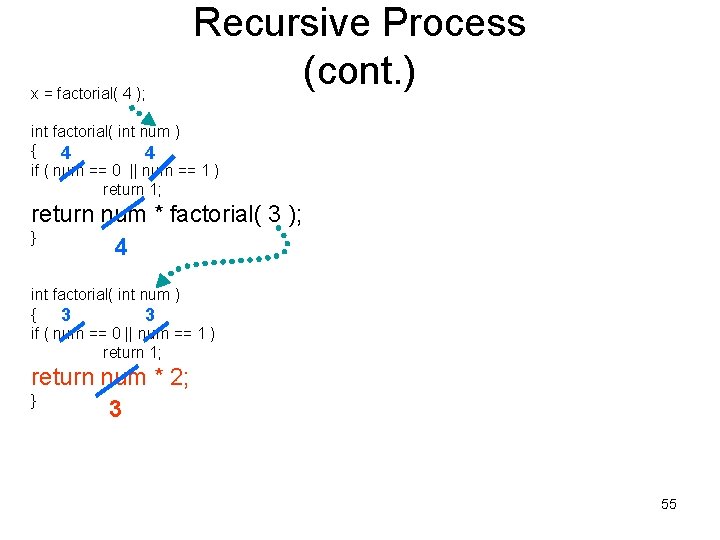
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return num * 2; } 3 55

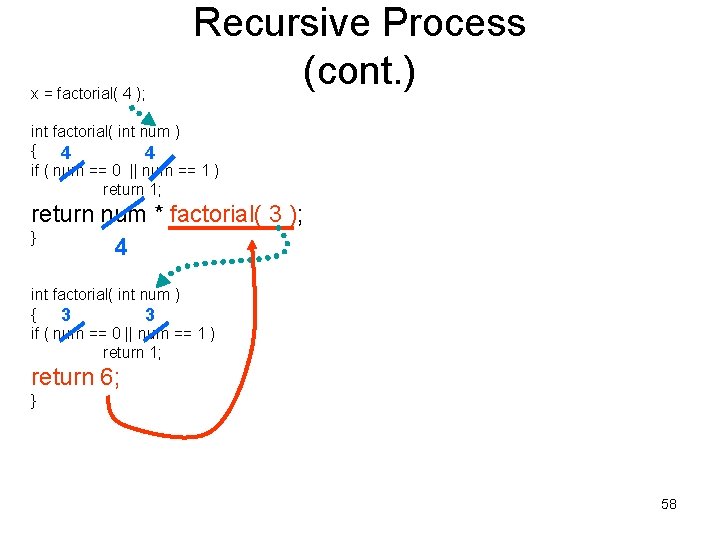
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return 6; } 56

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return 6; } 57

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * factorial( 3 ); } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return 6; } 58

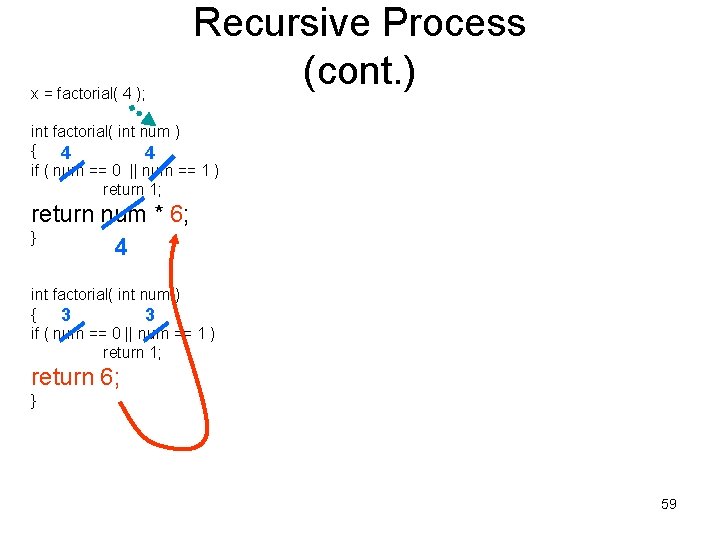
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * 6; } 4 int factorial( int num ) { 3 3 if ( num == 0 || num == 1 ) return 1; return 6; } 59

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * 6; } 4 60

x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return num * 6; } 4 61

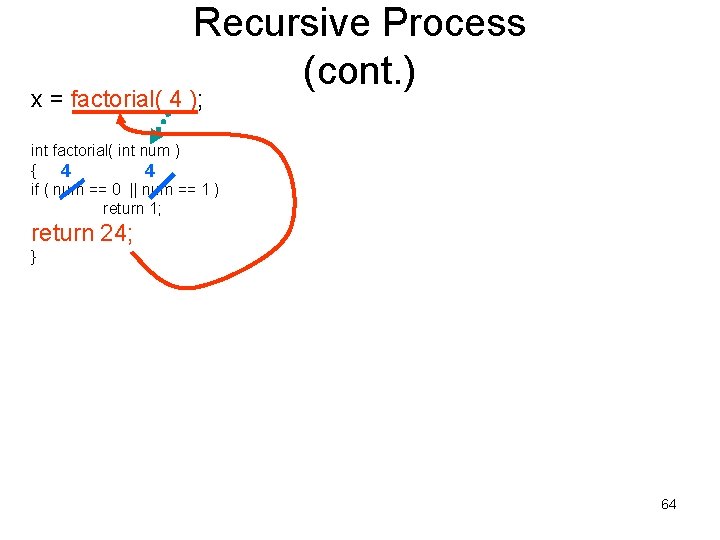
x = factorial( 4 ); Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return 24; } 62

Recursive Process (cont. ) x = factorial( 4 ); int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return 24; } 63

Recursive Process (cont. ) x = factorial( 4 ); int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return 24; } 64

Recursive Process (cont. ) x = factorial( 4 ); int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return 24; x gets the correct value of 24 } 65

x = 24; Recursive Process (cont. ) int factorial( int num ) { 4 4 if ( num == 0 || num == 1 ) return 1; return 24; x gets the correct value of 24 } 66

x = 24; Recursive Process (cont. ) 67

Base Case 1 2 3 4 5 6 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } Notice that these lines stopped the recursion – without these lines, the function will call itself over and over again (infinite recursion) 68

Base Case (cont. ) 1 2 3 4 5 6 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } These lines are called the base case – the case that stops the recursion 69

Recursive Case 1 2 3 4 5 6 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } This line that produces a recursive function call is called the recursive case. All recursive functions have a base case and a recursive case (and sometimes more than one of each). 70

What If? 1 2 3 4 5 6 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } If one makes a mistake and inputs a negative number into this function: factorial( -2 ); what will happen? 71

Infinite Recursion 1 2 3 4 5 6 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } If one makes a mistake and inputs a negative number into this function: factorial( -2 ); what will happen? Infinite recursion. 72

Drivers 1 2 3 4 5 6 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } In order to prevent this problem, we can change the name of this function to factorial 2… 73

Drivers 1 2 3 4 5 6 int factorial( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } In order to prevent this problem, we can change the name of this function to factorial 2… 74

Drivers (cont. ) 1 2 3 4 5 6 int factorial 2( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } In order to prevent this problem, we can change the name of this function to factorial 2… 75

Drivers (cont. ) 1 2 3 4 5 6 int factorial 2( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial( num – 1 ); } In order to prevent this problem, we can change the name of this function to factorial 2… 76

Drivers (cont. ) 1 2 3 4 5 6 int factorial 2( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial 2( num – 1 ); } In order to prevent this problem, we can change the name of this function to factorial 2… 77

Drivers (cont. ) 1 2 3 4 5 6 int factorial 2( int num ) { if ( num == 0 || num == 1 ) return 1; return num * factorial 2( num – 1 ); } and then write a factorial function, called a driver, to call this function… 78

Drivers (cont. ) int factorial( int num ) { if ( num < 0 ) { cout << “The factorial of a negative number is undefined” << endl; return 0; } return factorial 2( num ); } 79

Guidelines • There must be a base case that stops recursion • Each recursive call should approach the base case • The recursive function call should work for the case next to the base case • The recursive function should make logical sense, assuming that the recursive function call inside it does everything it should do 80

Example • When you know the case next to the base case works, you know factorial( 2 ) works • Since 3! = 3 * factorial( 2 ), you know factorial( 3 ) works – makes logical sense • Since 4! = 4 * factorial( 3 ) and you know that factorial( 3 ) works, you know that factorial( 4 ) works • Etc. , etc. 81

Recursion on a Linked List Car search( Node<Car> *ptr, Car mercedes ) { if ( ptr->info == mercedes ) return ptr->info; return search( ptr->next, mercedes ); } For use when we know Mercedes is in a linked list Initial call: Car auto = search( start, mercedes ); 82

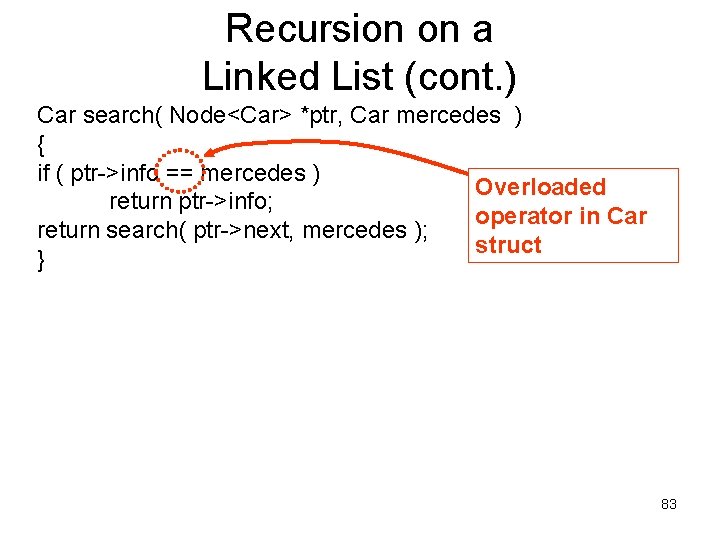
Recursion on a Linked List (cont. ) Car search( Node<Car> *ptr, Car mercedes ) { if ( ptr->info == mercedes ) Overloaded return ptr->info; operator in Car return search( ptr->next, mercedes ); struct } 83

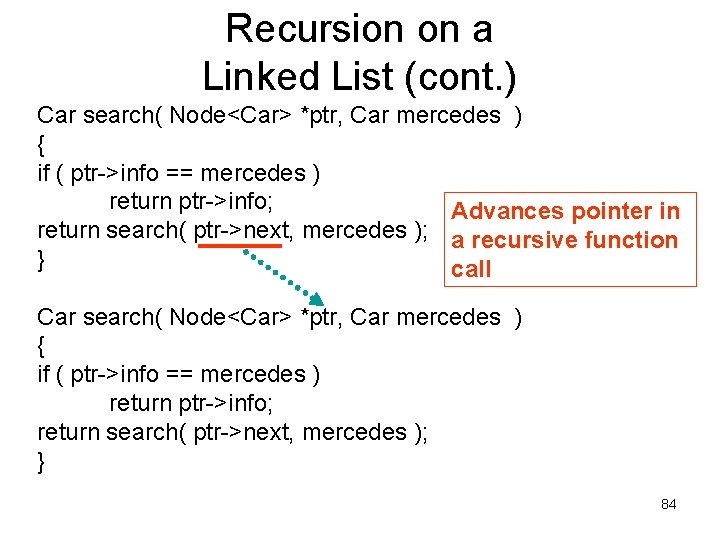
Recursion on a Linked List (cont. ) Car search( Node<Car> *ptr, Car mercedes ) { if ( ptr->info == mercedes ) return ptr->info; Advances pointer in return search( ptr->next, mercedes ); a recursive function } call Car search( Node<Car> *ptr, Car mercedes ) { if ( ptr->info == mercedes ) return ptr->info; return search( ptr->next, mercedes ); } 84

Recursion on a Linked List (cont. ) bool search( Node<Car> *ptr, Car & auto, Car mercedes ) { if ( ptr == NULL ) return false; if ( ptr->info == mercedes ) { auto = ptr->info; return true; } return search( ptr->next, auto, mercedes ); } For use when we are not sure there is a Mercedes in the linked list. 85

Recursion on a Linked List (cont. ) bool search( Node<Car> *ptr, Car & auto, Car mercedes ) { if ( ptr == NULL ) return false; if ( ptr->info == mercedes ) { auto = ptr->info; return true; } return search( ptr->next, auto, mercedes ); } Returns true if in list; returns false otherwise. 86

Recursion on a Linked List (cont. ) bool search( Node<Car> *ptr, Car & auto, Car mercedes ) { if ( ptr == NULL ) If true is returned, return false; auto will be assigned if ( ptr->info == mercedes ) { Mercedes (passed by auto = ptr->info; reference on each return true; recursive call) } return search( ptr->next, auto, mercedes ); } 87

Recursion on a Linked List (cont. ) bool search( Node<Car> *ptr, Car & auto, Car mercedes ) { if ( ptr == NULL ) Two return false; base if ( ptr->info == mercedes ) { cases auto = ptr->info; return true; } return search( ptr->next, auto, mercedes ); } 88

Recursion on a Linked List (cont. ) bool search( Node<Car> *ptr, Car & auto, Car mercedes ) { if ( ptr == NULL ) return false; if ( ptr->info == mercedes ) { auto = ptr->info; return true; } return search( ptr->next, auto, mercedes ); } Don’t forget the return ( it is a common mistake)… 89

Recursion on a Linked List (cont. ) bool search( Node<Car> *ptr, Car & auto, Car mercedes ) { if ( ptr == NULL ) return false; if ( ptr->info == mercedes ) { auto = ptr->info; return true; } return search( ptr->next, auto, mercedes ); } It passes the true/false value (from base cases) back through the succession of recursive function calls. 90

Recursion on a Linked List (cont. ) 1 2 3 4 5 6 7 void discount( Node<Car> *ptr ) { if ( ptr != NULL ) { ptr->info. price -= 0. 1 * ( ptr->info. price ); discount( ptr->next ); } } Discounts all auto prices in a linked list by 10% 91

Recursion on a Linked List (cont. ) 1 2 3 4 5 6 7 void discount( Node<Car> *ptr ) { if ( ptr != NULL ) { ptr->info. price -= 0. 1 * ( ptr->info. price ); discount( ptr->next ); } } Recursive call – no return necessary (void return type) 92

Recursion on a Linked List (cont. ) 1 2 3 4 5 6 7 void discount( Node<Car> *ptr ) { if ( ptr != NULL ) { ptr->info. price -= 0. 1 * ( ptr->info. price ); discount( ptr->next ); } } Where is the base case? 93

Recursion on Linked Lists (cont. ) 1 2 3 4 5 6 7 void discount( Node<Car> *ptr ) { if ( ptr != NULL ) { ptr->info. price -= 0. 1 * ( ptr->info. price ); discount( ptr->next ); } } The base case exists, it just does not need to be written. When ptr == NULL, it is the base case. The only thing that needs to be done for the base case is to return. 94

Time Complexities for Recursion • Recursion is an alternative to a loop • Recursion is never necessary – anything that can be done with recursion can be done with a loop • Just as we would estimate how many times a loop iterates, we must estimate how many times a recursive function is called – this gives the time complexity 95

Time Complexities for Recursion (cont. ) 1 2 3 4 5 6 7 void discount( Node<Car> *ptr ) { if ( ptr != NULL ) { ptr->info. price -= 0. 1 * ( ptr->info. price ); discount( ptr->next ); } This function is called recursively, once for } each of the n elements in a linked list, plus one more time for when ptr == NULL, giving us a total number of n + 1 calls – 96