C 20 0046 Database Management Systems Lecture 25

C 20. 0046: Database Management Systems Lecture #25 Matthew P. Johnson Stern School of Business, NYU Spring, 2004 M. P. Johnson, DBMS, Stern/NYU, Sp 2004 1

Agenda n n Previously: Hardware & sorting Next: q q q Indices Failover/recovery Data warehousing & mining n n Hw 3 due Thursday q n n Websearch no extensions! 1 -minute responses XML links up M. P. Johnson, DBMS, Stern/NYU, Sp 2004 2

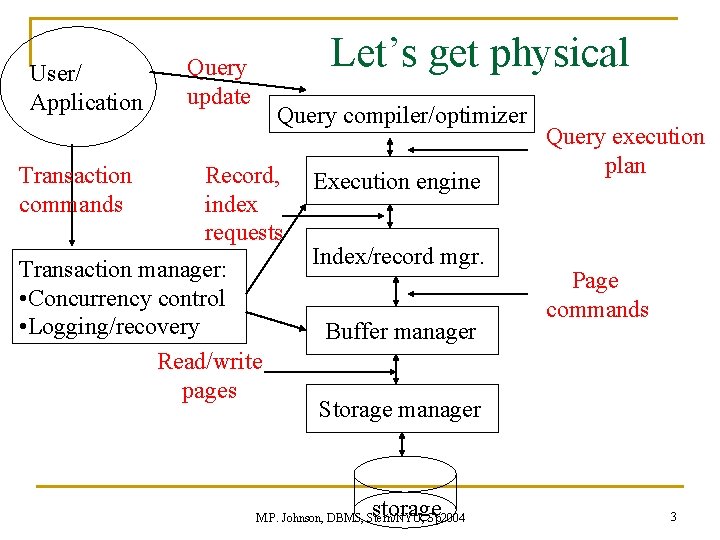
User/ Application Transaction commands Let’s get physical Query update Query compiler/optimizer Record, index requests Transaction manager: • Concurrency control • Logging/recovery Read/write pages Execution engine Index/record mgr. Buffer manager Query execution plan Page commands Storage manager storage M. P. Johnson, DBMS, Stern/NYU, Sp 2004 3

Hardware/memory review n DBs won’t fit in RAM Disk access is O(100, 000) times slower than RAM Model of Computation n q n I/O Model of Computation q q q n Single ops about same as single memory access We read/write one block (4 k) at a time Measure time in # disk accesses Ignore processor operations – O(100, 000) times faster Regular Mergesort q Divide in half each time and recurse M. P. Johnson, DBMS, Stern/NYU, Sp 2004 4

Hardware/memory review n Big problem: how to sort 1 GB with 1 MB of RAM? q n Soln: TPMMS (External Merge. Sort) 1. 2. 3. n Can use MS but must read/write all data 19+ times Sort data in 1 MB chunks Sort 249 of the chunks into a 249 MB chunk Sort 249 of the 249 MB chunks… Each iteration: q RAM size/blocksize * last-chunk-size M. P. Johnson, DBMS, Stern/NYU, Sp 2004 5

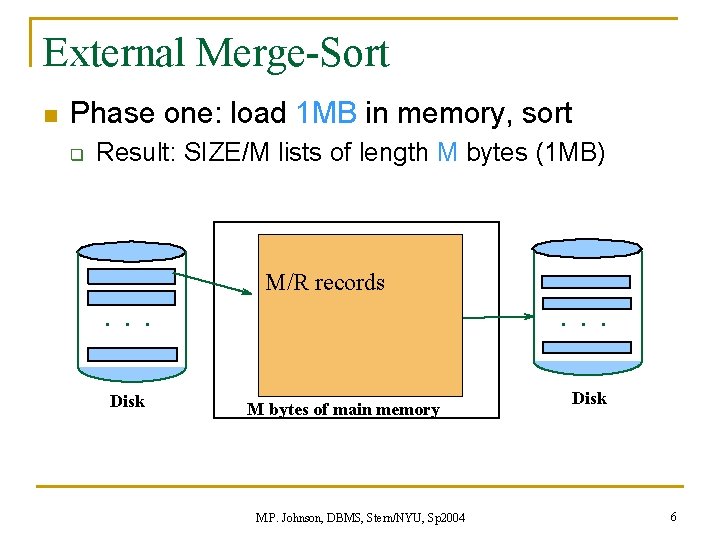
External Merge-Sort n Phase one: load 1 MB in memory, sort q Result: SIZE/M lists of length M bytes (1 MB) . . . Disk M/R records M bytes of main memory M. P. Johnson, DBMS, Stern/NYU, Sp 2004 . . . Disk 6

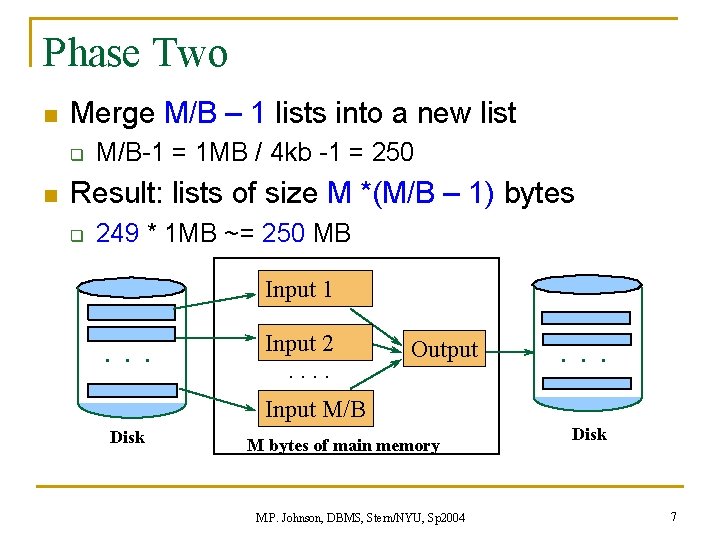
Phase Two n Merge M/B – 1 lists into a new list q n M/B-1 = 1 MB / 4 kb -1 = 250 Result: lists of size M *(M/B – 1) bytes q 249 * 1 MB ~= 250 MB Input 1 . . . Input 2. . Output . . . Input M/B Disk M bytes of main memory M. P. Johnson, DBMS, Stern/NYU, Sp 2004 Disk 7

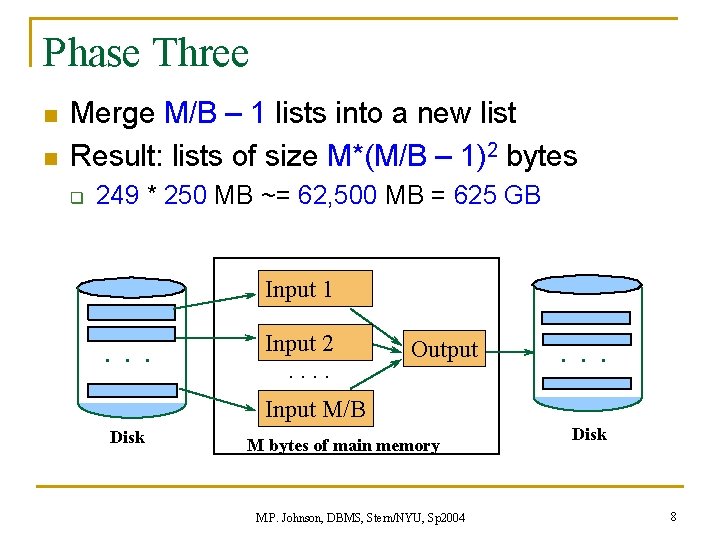
Phase Three n n Merge M/B – 1 lists into a new list Result: lists of size M*(M/B – 1)2 bytes q 249 * 250 MB ~= 62, 500 MB = 625 GB Input 1 . . . Input 2. . Output . . . Input M/B Disk M bytes of main memory M. P. Johnson, DBMS, Stern/NYU, Sp 2004 Disk 8

Next topic: File organization 1 n Heap files: unordered list of rows q n All row queries are easy: q n n One damn row after another. SELECT * FROM T; Insert is easy: just add to end Unique/subset queries are hard: q Must test each row M. P. Johnson, DBMS, Stern/NYU, Sp 2004 9

File organization 2 n Sorted file: sort rows on some fields Since datafile likely to be large, must use an external sort like external MS n Equality, range select now easier: n q q n Insert, delete now hard q n Do binary search to find first Walk through rows until one fails test Must move avg of half rows forward or back Possible solns: q q Leave empty space Use “overflow” pages M. P. Johnson, DBMS, Stern/NYU, Sp 2004 10

Modifications n Insert: File is unsorted easy q File is sorted: n Is there space in the right block? q n n If anything else fails, create overflow block Delete: Free space in block q Maybe be able to eliminate an overflow block n n Then store it there If not, use a tombstone (null record) Update: new rec is shorter than prev. easy q If it’s longer, need to shift records, create overflow blocks M. P. Johnson, DBMS, Stern/NYU, Sp 2004 11

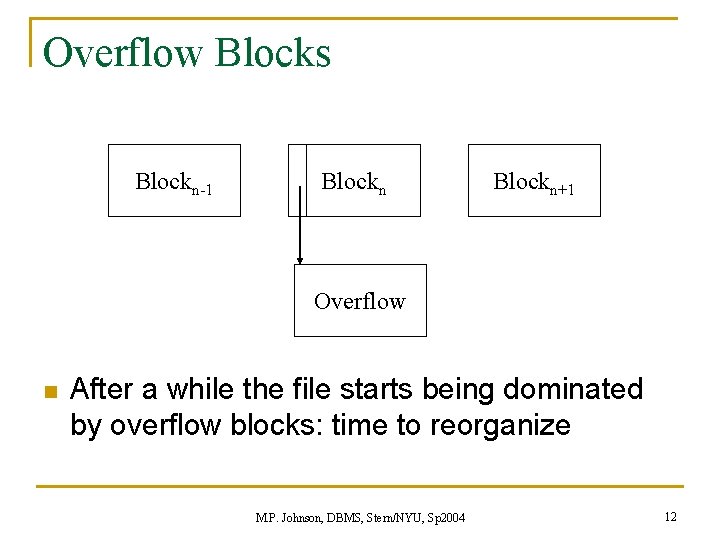
Overflow Blocks Blockn-1 Blockn+1 Overflow n After a while the file starts being dominated by overflow blocks: time to reorganize M. P. Johnson, DBMS, Stern/NYU, Sp 2004 12

File organization 3 n Datafile (un/sorted) + index n Speeds searches based on its fields q q Any subset/list of table’s fields these called search key n n Idea: trade disk space for disk time q n not to be confused with table’s keys/superkeys also may cost processor/RAM time Downsides: q q Takes up more space Must reflect changes in data M. P. Johnson, DBMS, Stern/NYU, Sp 2004 13

Classification of indices n Primary v. secondary Clustered v. unclustered Dense v. sparse n Index data structures: n n q q n B-trees Hash tables More advanced types: q q q Function-based indices R-trees Bitmap indices M. P. Johnson, DBMS, Stern/NYU, Sp 2004 14

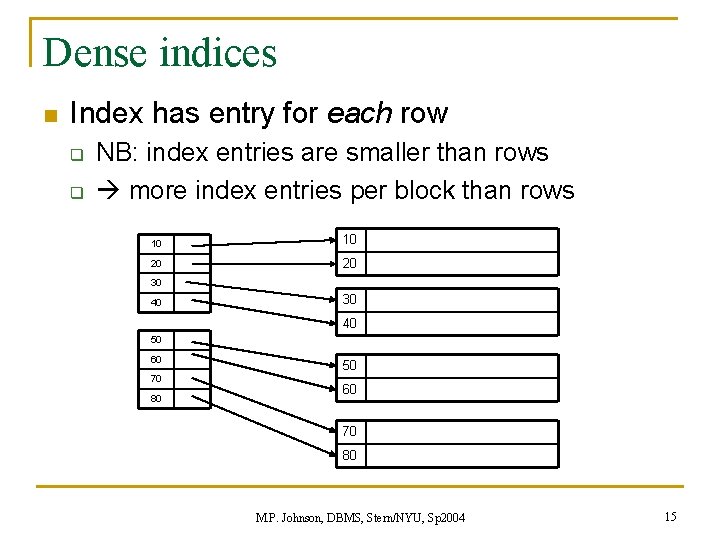
Dense indices n Index has entry for each row q q NB: index entries are smaller than rows more index entries per block than rows 10 10 20 20 30 40 50 60 70 80 M. P. Johnson, DBMS, Stern/NYU, Sp 2004 15

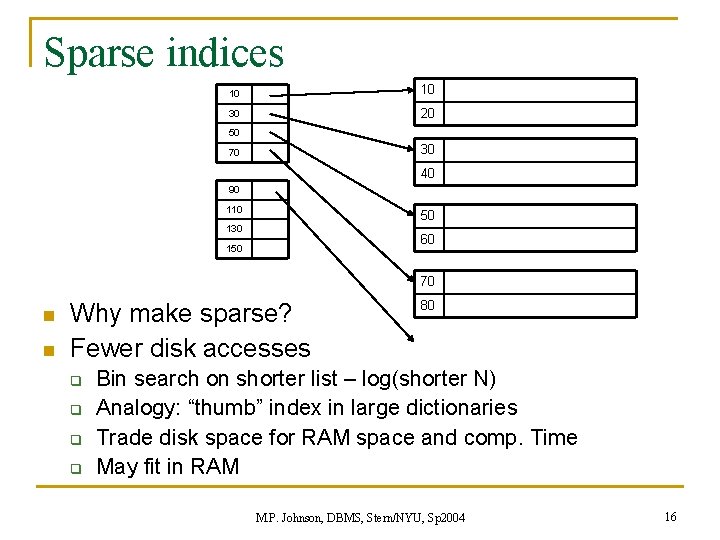
Sparse indices 10 10 30 20 50 30 70 40 90 110 50 130 60 150 70 n n Why make sparse? Fewer disk accesses q q 80 Bin search on shorter list – log(shorter N) Analogy: “thumb” index in large dictionaries Trade disk space for RAM space and comp. Time May fit in RAM M. P. Johnson, DBMS, Stern/NYU, Sp 2004 16

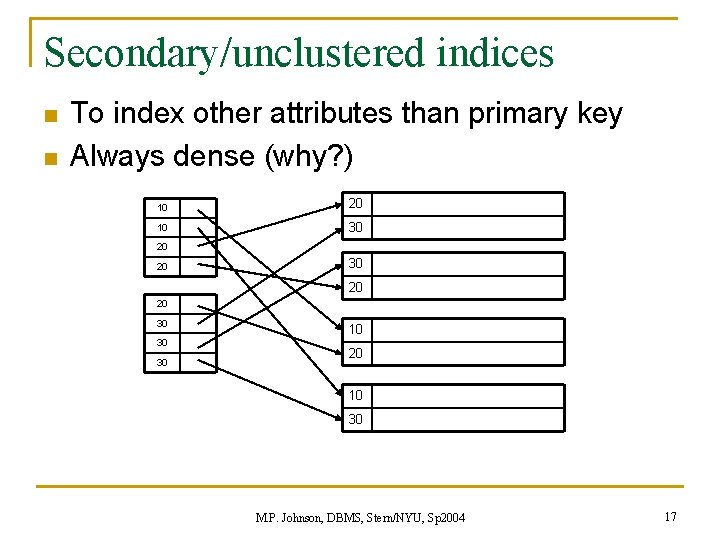
Secondary/unclustered indices n n To index other attributes than primary key Always dense (why? ) 10 20 10 30 20 20 30 30 30 10 20 10 30 M. P. Johnson, DBMS, Stern/NYU, Sp 2004 17

Clustered v. unclustered n Clustered means: data and index sorted same way q q n Sparse indices must be clustered q n Sorted on the fields the index is indexing Each index entry stored “near” data entry Unclustered indices must be dense Clustered indices can reduce disk latency q q Related data stored together – less far to go Good for range queries M. P. Johnson, DBMS, Stern/NYU, Sp 2004 18

Primary v. secondary n Primary indexes q q q n usually clustered Only one per table Use PRIMARY KEY Secondary indexes q q q usually unclustered many allowed per table Use UNIQUE or CREATE INDEX M. P. Johnson, DBMS, Stern/NYU, Sp 2004 19

Partial key searches n Situ: index on fields a 1, a 2, a 3; we search on fields ai, aj n When will this work? i and j must be 1 and 2 (in either order) 1. n n 2. Searched fields must be a prefix of the indexed fields E. g. : lastname, firstname in phone book Index must be clustered M. P. Johnson, DBMS, Stern/NYU, Sp 2004 20

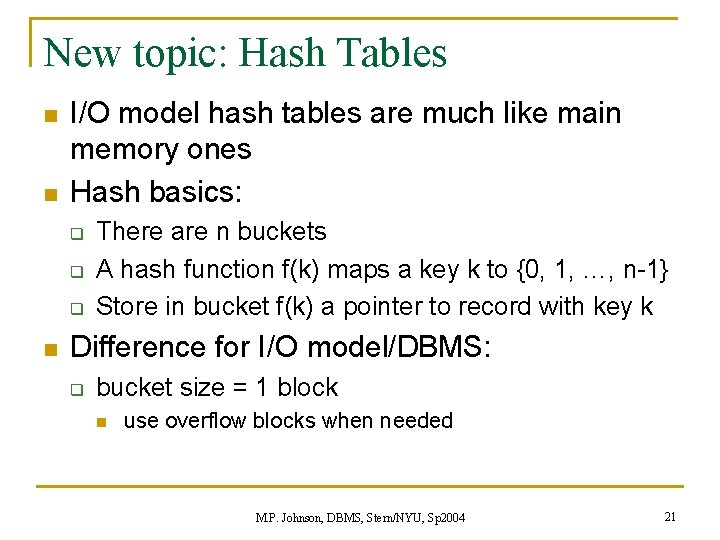
New topic: Hash Tables n n I/O model hash tables are much like main memory ones Hash basics: q q q n There are n buckets A hash function f(k) maps a key k to {0, 1, …, n-1} Store in bucket f(k) a pointer to record with key k Difference for I/O model/DBMS: q bucket size = 1 block n use overflow blocks when needed M. P. Johnson, DBMS, Stern/NYU, Sp 2004 21

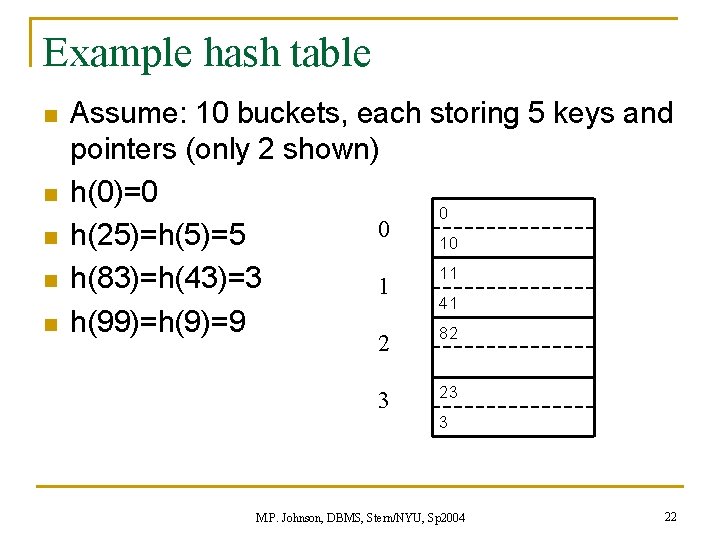
Example hash table n n n Assume: 10 buckets, each storing 5 keys and pointers (only 2 shown) h(0)=0 0 0 h(25)=h(5)=5 10 11 h(83)=h(43)=3 1 41 h(99)=h(9)=9 82 2 3 23 3 M. P. Johnson, DBMS, Stern/NYU, Sp 2004 22

Hash table search n Search for 82: q q q Compute h(82)=2 Read bucket 2 1 disk access 0 10 11 41 2 82 3 23 3 M. P. Johnson, DBMS, Stern/NYU, Sp 2004 23

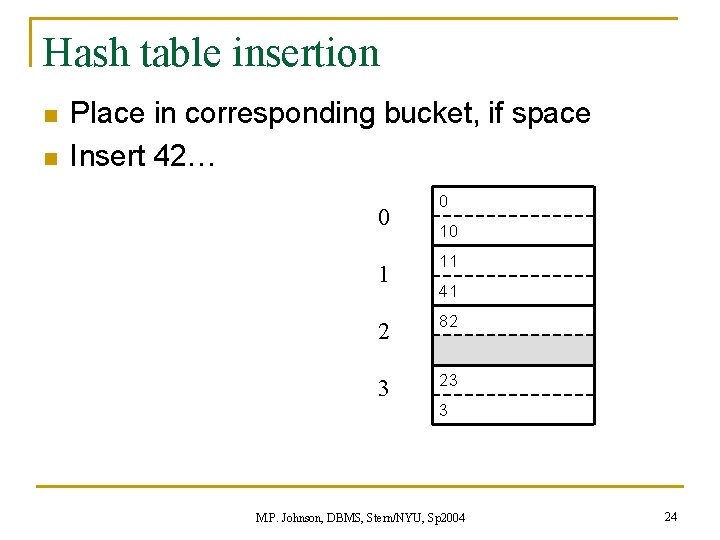
Hash table insertion n n Place in corresponding bucket, if space Insert 42… 0 10 11 41 2 82 3 23 3 M. P. Johnson, DBMS, Stern/NYU, Sp 2004 24

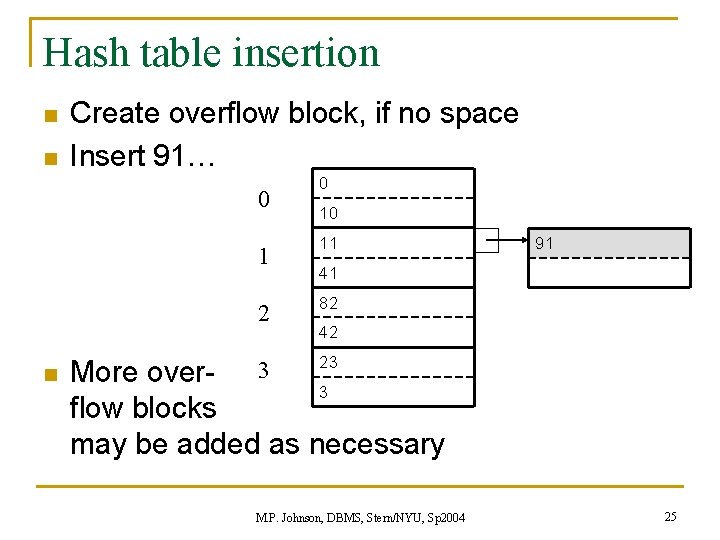
Hash table insertion n n Create overflow block, if no space Insert 91… 0 1 2 n 0 10 11 91 41 82 42 23 More over- 3 3 flow blocks may be added as necessary M. P. Johnson, DBMS, Stern/NYU, Sp 2004 25

Hash table performance n n n Excellent if no overflow blocks For in-memory indices, hash tables usually preferred Performance degrades as ratio of keys/(n*blocksize) increases M. P. Johnson, DBMS, Stern/NYU, Sp 2004 26

Hash functions n n Lots of ideas for “good” functions, depending on situation One obvious idea: h(x) = x mod n q q q n Every x mapped to one of 0, 1, …, n-1 Roughly 1/nth of x’s mapped to each bucket Does this work for equality search? Does this work for range search? Does this work for partial-key search? Good functions of hashing passwords? q What was the point of hashing in that case? M. P. Johnson, DBMS, Stern/NYU, Sp 2004 27

Extensible hash table n Number of buckets grows to prevent overflows n Also used for crypto, hashing passwords, etc. And: Java’s Hash. Map and object. hash. Code() n M. P. Johnson, DBMS, Stern/NYU, Sp 2004 28

New topic: B-trees n Saw connected, rooted graphs before: XML graphs n Trees are connected, acyclic graphs n Saw rooted trees before: q q q n XML docs directory structure on hard drive Organizational/management charts B-trees are one kind of rooted tree M. P. Johnson, DBMS, Stern/NYU, Sp 2004 29

Twenty Questions n What am I thinking of? q q q n Strategy: q q n Large space of possible choices Can ask only yes/no questions Each gives <=1 bit ask questions that divide searchspace in half gain full bit from each question log 2(1, 000 ~= 220) = 20 M. P. Johnson, DBMS, Stern/NYU, Sp 2004 30

BSTs n Very simple data structure in CS: BSTs q q q n Each node has two children: q q n Binary Search Trees Keep balanced Each node ~ one item Left subtree: < Right subtree: >= Can search, insert, delete in log time q log 2(1 MB = 220) = 20 M. P. Johnson, DBMS, Stern/NYU, Sp 2004 31

Search for DBMS n Big improvement: log 2(1 MB) = 20 q Each op divides remaining range in half! n But recall: all that matters is #disk accesses n 20 is better than 220 but: Can we do better? M. P. Johnson, DBMS, Stern/NYU, Sp 2004 32

BSTs B-trees n n Like BSTs except each node ~ one block Branching factor is >> 2 q q q n Data stored only in leaves q q n Each access divides remaining range by, say, 300 B-trees = BSTs + blocks B+ trees are a variant of B-trees Leaves form a (sorted) linked list Better supports range queries Consequences: q q q Much shorter depth Many fewer disk reads Must find element within node Trades CPU/RAM time for disk time M. P. Johnson, DBMS, Stern/NYU, Sp 2004 33

B-tree search efficiency n With params: q q q n the largest n satisfying 4 n+8(n+1) <= 4096 is n=340 q q n block=4 k integer = 4 b, pointer = 8 b Each node has 170. . 340 keys assume on avg has (170+340)/2=255 Then: q q 255 rows depth = 1 2552 = 64 k rows depth = 2 2553 = 16 M rows depth = 3 2554 = 4 G rows depth = 4 M. P. Johnson, DBMS, Stern/NYU, Sp 2004 34

Next time n Next: Failover For next time: reading online n Hw 3 due next time n q n no extensions! Now: one-minute responses M. P. Johnson, DBMS, Stern/NYU, Sp 2004 35