Byzantine Fault Tolerance in BFT Greg Bronevetsky Byzantine

Byzantine Fault Tolerance in BFT Greg Bronevetsky

Byzantine Failure Tolerance via Replication Run a program multiple times and compare the results of different runs. � Pro: Much work done in this area and working solutions exist. � Con: Typical systems incur about 200% overhead in time and/or resources �

BFT Background � BFT = “Byzantine Fault Tolerance” Library created at the MIT Laboratory of Computer Science by Miguel Castro and Barbara Liskov. � Uses replication to make services Byzantine Fault-Tolerant. � BFS is a Byzantine Fault-Tolerant implementation of the NFS file system. �

System Model Network delivers messages eventually but messages may be delayed, duplicated or delivered out of order. � Node Failures assumed to be independent. � Non-faulty nodes cannot be delayed indefinitely. � All messages are cryptographically signed by their sender and these signatures cannot be subverted by the adversary. (Thus, the sender of every message is known. ) �

Service Properties A service is replicated among ≥ 3 f+1 processors. Resilient to ≤ f failures. � Safety – All replicas guaranteed to process the same requests in the same order. Thus, if each replica implements the same deterministic service and starts in the same state, then all replicas will end up in the same state. � Liveness – Clients are guaranteed to eventually receive replies to all requests. �

Limitations � Faulty Clients may corrupt system state if they have proper access. � Fault-Tolerant Privacy is not addressed.

Overall Structure � There are 3 f+1 replicas, one of which is the primary P, which initiates the protocols. The primary still implements the service and services requests. Execution is broken up into views. During view v, replica Rv (mod 3 f+1) serves as the primary. � If view v's primary is faulty, the non-faulty replicas vote to enter view v+1, with a new primary. �

Overall Structure: Request Step 1: A Client sends a request to what it believes to be the Primary P. If that replica is not the primary, it forwards the request. R 2 Ri R 1 P R 3 f-1 R 3 f Request Client

Overall Structure: Agreement Step 2: Non-faulty replicas agree on a sequence number for this request, ensuring all requests are processed in same order. R 2 Protocol R 1 ot oc Ri Protocol P l o c l t Pro c o t o r o P ol Protocol Pr oco to o r P l P r o t o c o l Rn-2 Protocol R n-1 Client

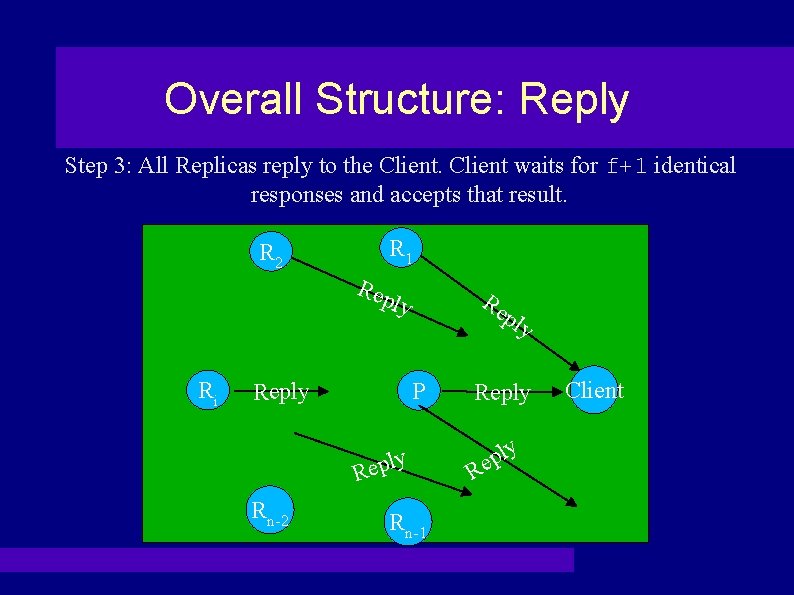
Overall Structure: Reply Step 3: All Replicas reply to the Client waits for f+1 identical responses and accepts that result. R 1 R 2 Rep Re ly Ri ply P Reply R Rn-2 Rn-1 Reply R ly p e Client

Overall Structure: Faulty Primary If the Client does not receive a response in time, it broadcasts the request to all replicas. (If P does not pass requests on to the group, it will be suspected as faulty by the group) R 2 R 1 Re qu est Req uest P Request Client t s e u Req st e qu e R Ri R 3 f-1 R 3 f

Understanding Byzantine Agreement Most of the protocols used in the system are specialized versions of the same Byzantine Agreement protocol. � These protocols ensure that all client requests are executed in the same order on all replicas. �

Optimal Resiliency � The use of 3 f+1 replicas to tolerate f failures is optimal. � � � Imagine the non-faulty processors trying to agree upon a piece of data by telling each other what they believe the data to be. A non-faulty processor must be sure about a piece of data before it can proceed. f replicas may refuse to send messages, so each processor must be ready to proceed after having received (n-1)-f messages. (total of n-1 other replicas)

Optimal Resiliency � � But what if f of the (n-1)-f messages come from faulty replicas? ≥f of the n-f-1 messages must come from nonfaulty nodes to avoid confusion. (for a majority total of ≥f+1 non-faulty votes) � Thus, each replica requires ≥f+f+f=3 f neighbors. � Need a total of ≥ 3 f+1 replicas.

Basic Agreement Protocol The Primary P has value d that it wishes for all replicas to agree upon. R 2 R 1 P Ri Rn-2 Rn-1

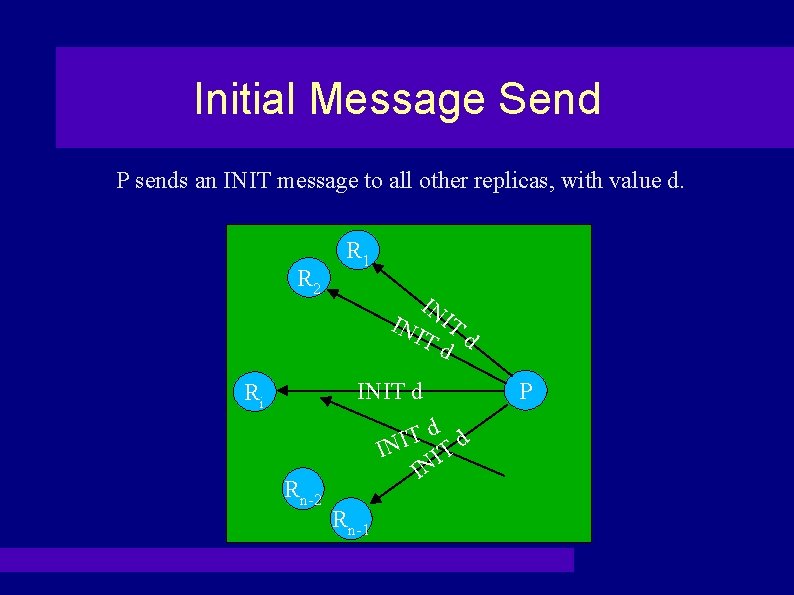
Initial Message Send P sends an INIT message to all other replicas, with value d. R 2 R 1 IN INI IT Td d INIT d Ri Rn-2 d d T I IN IT IN Rn-1 P

Final Message Send When Ri receives INIT d, it sends a FIN message to all other replicas with the value d that it received. R 1 FIN d FI N d R 2 Ri FIN d d N FI d FIN Rn-2 Rn-1 P

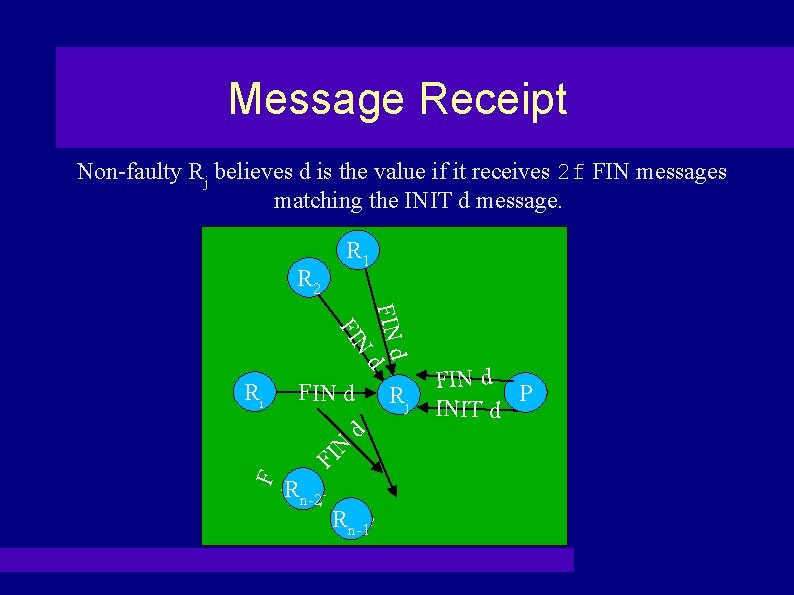
Message Receipt Non-faulty Rj believes d is the value if it receives 2 f FIN messages matching the INIT d message. R 2 R 1 FIN dd N FI Ri Rn-2 Rn-1 d F I N F IN d FIN d Rj FIN d P INIT d

Agreement Achieved � Guarantee: � If primary is non-faulty then all 2 f+1 non-faulty replicas agree on value of d. AND � If primary is faulty, either � OR � � ≥f+1 non-faulty replicas (majority) agree on some value and the rest realize that the primary is faulty. All non-faulty replicas will suspect the primary is faulty. Note: goal is to agree on some value. There is no erroneous value of d to avoid.

Agreement Achieved? � Does this really work? � What are the possible ways for the faulty replicas to subvert agreement? � Let Gi be the 2 f+1 non-faulty replicas (Good) � Let Bj be the f faulty replicas (Bad) Primary P initiates the agreement protocol. �

Case 1: PP is non-faulty P sends INIT message to all replicas, with correct d. Gi G 1 INIT IT d d INIT d IN G 2 f d T I N d I T I IN N I P Bf d Bj T I B 1

PP is non-faulty: FIN Worst Case: Replica Gi receives f messages from all the Bj with erroneous data d' and 2 f correct d messages. G 2 f FIN Gi d FIN d FI N ' d I N F FIN d' B 1 Bj Bf G 1 d P

PP is non-faulty: Agreement Gi only believes in a value if it receives 2 f external confirmations of that value. � d' can only come from the FIN messages of f replicas. � Correct d comes from the FIN messages of 2 f replicas. � Thus, all non-faulty Gi's will agree on the same value d. �

PP is non-faulty: Key Behavior As long as the primary is working, the non-faulty replicas will agree.

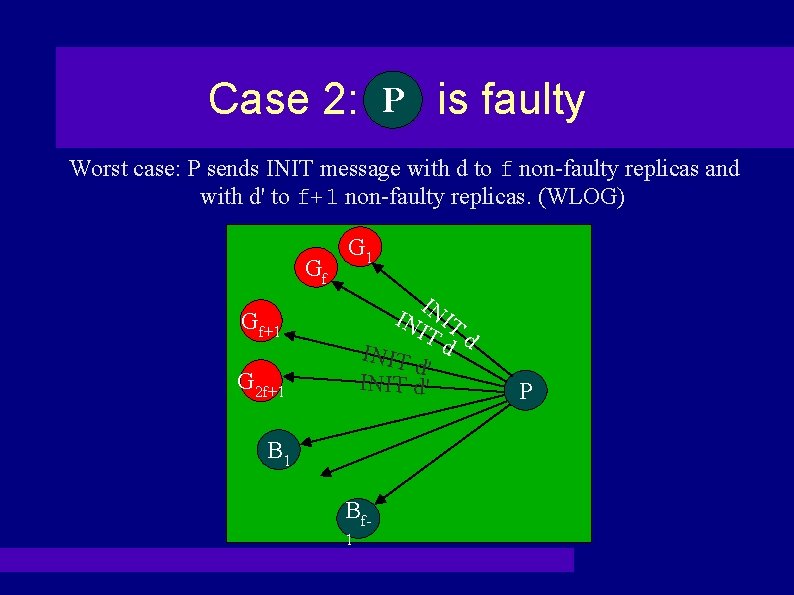
Case 2: PP is faulty Worst case: P sends INIT message with d to f non-faulty replicas and with d' to f+1 non-faulty replicas. (WLOG) Gf G 1 IN IN IT IT d INIT d d' INIT d' Gf+1 G 2 f+1 B 1 Bf 1 P

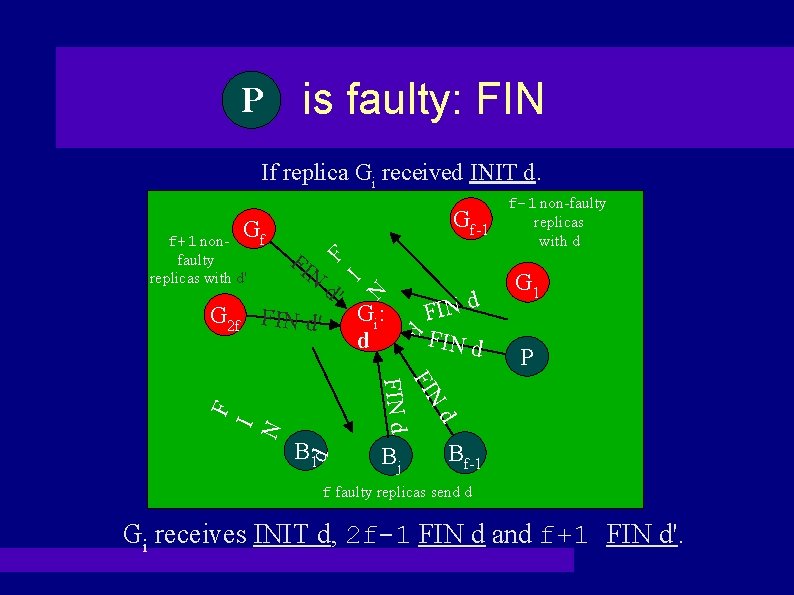
PP is faulty: FIN If replica Gi received INIT d. FI N d Gi : d FIN d G 1 P F d FIN d B 1 d I N N G 2 f FIN d' d' I f+1 nonfaulty replicas with d' Gf-1 F Gf f-1 non-faulty replicas with d Bj Bf-1 f faulty replicas send d Gi receives INIT d, 2 f-1 FIN d and f+1 FIN d'.

PP is faulty: FIN If replica Gi received INIT d'. Gi-1 Gi FI N B 1 ' d I N d N Gi : d' FIN d' G 1 P d' FIN d' F G 2 f FIN d' d' I F f non-faulty +1 replicas with d' f non-faulty replicas with d Bj Bf-1 f faulty replicas send d' Gi receives INIT d', f FIN d, and 2 f FIN d'.

PP is faulty: Agreement If non-faulty Gi received INIT d then it will receive 2 f-1 FIN d messages and will believe the primary to be faulty. � If non-faulty Gj received INIT d', then it will receive 2 f FIN d' messages and will believe that d' is the value. � Majority (f+1) of non-faulty nodes has agreed on d'.

PP � is faulty: Key Behavior Key Points in Agreement: � � � The confused non-faulty replicas (a minority) can now stop interacting and demand for a new primary. The majority of non-faulty replicas can go on as long as they can keep agreeing (if the faulty replicas help). If at some point the unconfused replicas can't agree, then all the non-faulty replicas will become confused and will elect a new primary.

Overall System Behavior The system works by repeating the above agreement protocol in several forms. � If the primary is non-faulty, agreement is easy. � If the primary is faulty then the majority of non-faulty replicas will agree on one course of action. � When a faulty primary is replaced, the minority of confused non-faulty replicas are brought upto date up by the majority. �

Recall: Request Step 1: A Client sends a request to what it believes to be the Primary P. If that replica is not the primary, it forwards the request. R 2 Ri R 1 P R 3 f-1 R 3 f Request Client

Recall: Agreement Step 2: Non-faulty replicas agree on a sequence number for this request, ensuring all requests are processed in same order. R 2 Protocol R 1 ot oc Ri P Protocol l o c l t Pro c o t o r o P ol Protocol Pr oco to o r P l n-2 P r o t o c o l Rn-2 Protocol R Client

Recall: Reply Step 3: All Replicas reply to the Client waits for f+1 identical responses and accepts that result. R 1 R 2 Rep Re ly Ri ply P Reply R Rn-2 Reply R ly p e Client

Implementation of Agreement First: non-faulty replicas must agree on a given message's sequence number. � When the primary P receives a request, it sends to all replicas: � <PRE-PREPARE, v, n, d, m> v = current view number n = request's sequence number d = digest of the message m = the request message itself

Sequencing Requests � When a replica Ri receives <PRE-PREPARE, v, n, d, m>, it multicasts to all replicas <PREPARE, v, n, d, i>. (The primary also sends a PREPARE) � When some replica Ri receives <PREPARE, v, n, d, j> from 2 f different replicas that matches its PRE-PREPARE, it enters the PREPARED(m, v, n, i) state.

Prepared Replicas Since Ri entered the PREPARED(m, v, n, i) state via our Agreement protocol, we know: � ≥f+1 non-faulty replicas have sent a PREPREPARE or PREPARE for the same v, n, d and m. � No other non-faulty Rj is PREPARED with this sequence number for another message. � (because the majority has agreed on this number for this message)

From Prepare to Commit 1. Now we can rely on a core of ≥f+1 nonfaulty replicas that will eventually all become PREPARED and will agree on a sequence number for the request. The PRE-PREPARE and PREPARE phases of the protocol ensure agreement on the total order of requests within a view. � The PREPARE and COMMIT phases ensure total ordering across views. �

The Commit Phase Ends Replica Ri enters the COMMITED-LOCAL(m, v, n, i) state when it has become PREPARED(m, v, n, i) and has received 2 f matching <COMMIT, v, n, i> messages. � At this point we're sure that ≥f+1 non-faulty replicas Rj have become PREPARED(m, v, n, j). � Thus, COMMITTED(m, v, n) is true. �

The Commit Phase � When some replica Ri enters the PREPARED(m, v, n, i) state, it multicasts <COMMIT, v, n, d, i> to all other replicas. � Goal: a request m is considered COMMITTED(m, v, n) iff PREPARED(m, v, n, i) is true for f+1 non-faulty replicas. � Then we can service the request because we know that f+1 non-faulty replicas (majority) will do it in the right order.

Replies to the Client When a replica enters the COMMITED-LOCAL(m, v, n, i) state, it can safely execute the request, assured that a global decision on m's sequence number has been made. � The replica sends the reply to the client, which waits for f+1 identical replies. � � Barring a view change, we're done.

Garbage Collection Whenever a replica receives a message, it must save it in its log for possible future use. � When is it safe to discard old messages? � It is safe to discard messages upto sequence number n when the non-faulty replicas can all agree that they've committed all requests upto that number. � These Commitment Proofs act as Checkpoints that don't help with failure recovery. �

Checkpointing Round To ensure that all the non-faulty replicas have committed requests upto number n, we perform the agreement protocol again. � Each time Ri processes a constant number of requests (like 100), it multicasts to all replicas: � <CHECKPOINT, n, i>

Stable Checkpoints When Rj receives 2 f CHECKPOINT messages matching the message that it sent out, we know ≥f+1 non-faulty replicas have serviced requests with sequence numbers ≤n. � At this point we have a Stable Checkpoint. � Rj can discard all messages relating to sequence numbers n and below. �

View Changes When the primary is faulty, the non-faulty replicas must decide to move from view v to view v+1. � Recall that replica Rv (mod 3 f+1) is the primary of view v. � Recall that if a client does not receive a response to its request in time, it broadcasts the request to all replicas. � (so if the primary is refusing to transmit requests to replicas, the replicas will know about it)

View Change Protocol When replica Ri receives request m, it starts a timer. � If it does not manage to process the request within the allotted time, it multicasts <VIEW-CHANGE, v+1, n, C, P, i> to all replicas. � v+1 = number of the new view n = the sequence number of the last request checkpointed at Ri. C = proof of Ri's latest checkpoint. P = requests for which Ri has PREPARED(m, v, n, i).

View-Changed Replicas drop off � Once a replica sends a VIEW-CHANGE message, it ignores all messages besides CHECKPOINT, VIEW-CHANGE and NEW-VIEW. � We will wait for the majority of non-faulty replicas to decide to change views before moving to view v+1. i. e. replicas wait for 2 f VIEW-CHANGE messages.

Events before the View Change � Before the view change we have two groups of non-faulty replicas: the Confused minority and the Agreed majority. A non-faulty replica becomes Confused when it is kept by the faulty's from agreeing on a sequence number for a request. � It can't process this request and so it will time out, causing the replica to vote for a new view. �

Events before the View Change The minority Confused replicas send a VIEW -CHANGE message and drop off the network. � The majority Agreed replicas continue working as long as the faulty's help with agreement. � � The two groups can go out of synch but the majority keeps working until the faulty's cease helping with agreement.

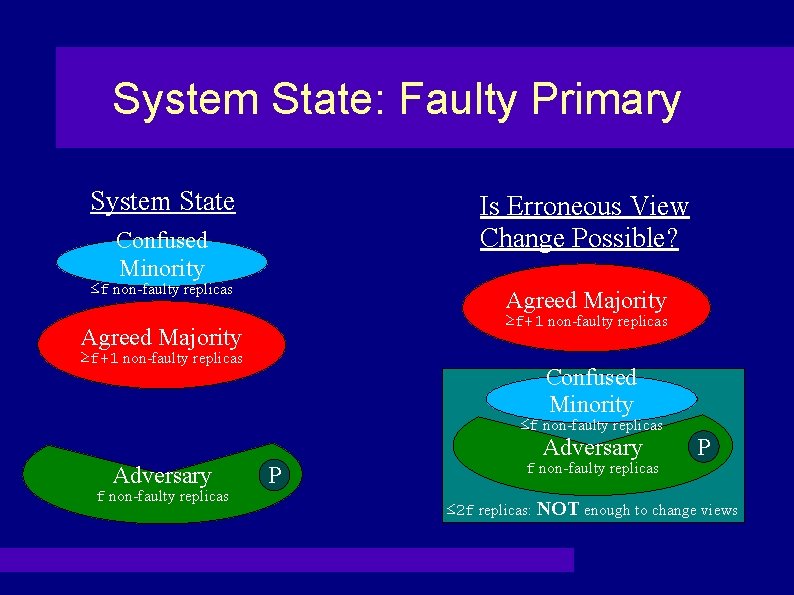
System State: Faulty Primary System State Is Erroneous View Change Possible? Confused Minority ≤f non-faulty replicas Agreed Majority ≥f+1 non-faulty replicas Confused Minority ≤f non-faulty replicas Adversary f non-faulty replicas P ≤ 2 f replicas: NOT enough to change views

Events before the View Change � Given ≥f+1 non-faulty replicas that are trying to agree, the faulty replicas can either help that or hinder that. ➲ ➲ � If they help, then agreement on request ordering is achieved and the clients get ≥f+1 matching replies for all requests where the faulty's help. If they hinder, then the ≥f+1 non-faulty's will time out and demand for a new view. When the new majority is in favor of a view change, we can proceed to the new view.

System State: Faulty Primary Is it possible to continue processing requests? P

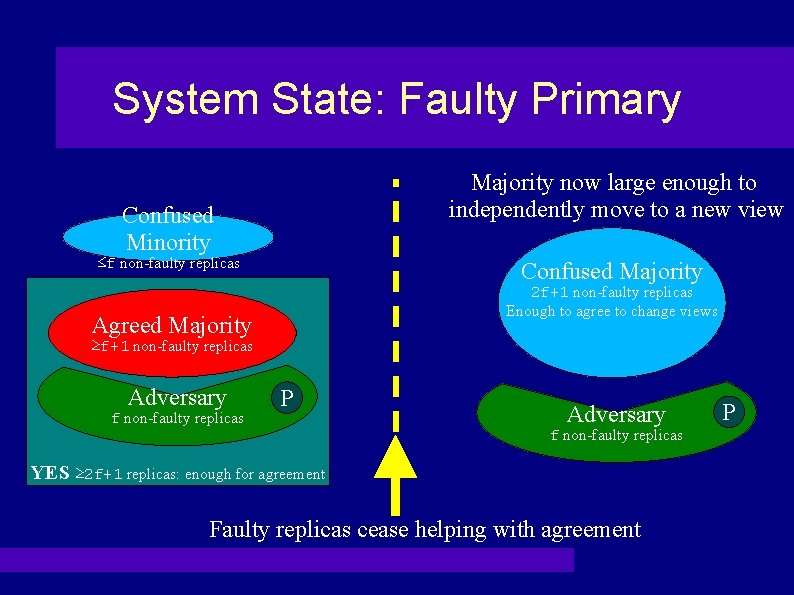
System State: Faulty Primary Majority now large enough to independently move to a new view Confused Minority ≤f non-faulty replicas Confused Majority 2 f+1 non-faulty replicas Enough to agree to change views Agreed Majority ≥f+1 non-faulty replicas Adversary f non-faulty replicas P Adversary f non-faulty replicas YES ≥ 2 f+1 replicas: enough for agreement Faulty replicas cease helping with agreement P

New-View Message � When the primary of view v+1 receives 2 f valid VIEW-CHANGE messages, it multicasts <NEW-VIEW, v+1, VC, O> to all replicas. � VC = 2 f valid VIEW-CHANGE messages that prove the validity of this view change. � O = New PRE-PREPARE messages that redo view v's un-checkpointed but PREPARED requests in view v+1.

Requests Across Views � But what happens if a few replicas already entered the COMMITED-LOCAL(m, v, n, i) state in view v and began executing the request BEFORE we switched to view v+1? � How will the new view deal with the partially executed operations of the old view?

Requests Across Views Recall: COMMITED-LOCAL(m, v, n, i) implies that ≥f+1 non-faulty replicas Rj have become PREPARED(m, v, n, j) � Thus, there ≥f+1 are such Rj's for each commit = set A. �

Requests Across Views Recall that Rk's VIEW-CHANGE message carries proofs of all PREPARED states. � The new primary's NEW-VIEW message carries with it 2 f+1 valid VIEW-CHANGE messages = set B. � � We only have 3 f+1 replicas so sets A and B must overlap on at least one replica.

Requests Across Views For each committed request (COMMITEDLOCAL), there will be at ≥ 1 replica in (A U B). � This replica PREPARED for this request and its VIEW-CHANGE message got bundled in the NEW-VIEW message. � Thus, the new view's primary knows that this request got prepared for by some replica(s). � It issues a new PRE-PREPARE message for this request, re-executing it. � Those replicas that have already executed it, resend the old results. �

Requests Across Views � But what of the requests that did not manage to get to COMMITTED(m, v, n) state in the old view? They either did not get prepared anywhere OR � They got prepared at too few replicas. � � Thus, they got executed nowhere, so we drop them. (clients will resend such requests when they time out)

Ensuring Liveness � Though we're sure that all requests are executed in proper order, can the faulty replicas delay us indefinitely? We must maximize the time period when ≥ 2 f+1 non-faulty replicas are in the same view. � Thus, must ensure that the faulty replicas cannot cause us to switch views too often. �

Ensuring Liveness When a replica sends a VIEW-CHANGE message, it waits for 2 f more such messages. � It now knows that the majority agrees to a view change. � The replica now starts a timer with an expiration period of T. �

Ensuring Liveness � If the timer expires before the replica receives a NEW-VIEW message for view v+1 or some messages that are in v+1, the primary is probably faulty. � Thus, the replica sends a VIEW-CHANGE message for view v+2, with a timeout of 2 T. (The increased timeout is to account for the case where the network is just really slow)

Ensuring Liveness If replica Ri receives f+1 VIEW-CHANGE messages for views greater than its current view, this implies that at least one non-faulty replica suspects the primary to be faulty. � Since we don't know which of these replicas is non-faulty, we'll be conservative: � Ri will send out a VIEW-CHANGE message for the smallest view in the set. � Thus, if one replica suspects the primary, all replicas will soon move to a new primary. �

Ensuring Liveness Unless f+1 (majority) non-faulty replicas already want to change views, the faulty replicas cannot force a view change. � Only a faulty primary can force a view change. � However, only f of the replicas can be faulty so ≤f consecutive views can have a faulty primary. �

Liveness Ensured � Thus, unless message delays grow indefinitely(unlikely) or the set of faulty nodes keeps rapidly changing, Liveness is Ensured.

The Replication Library � A general purpose library has been created on top of which Byzantine Fault-Tolerant services may be created. � An implementation of an NFS server, called BFS has been created on top of the replication library.

Performance Evaluation: Pure Overhead � Comparison between BFS and a bare-bones unreplicated NFS implementation. Tested read/write and read-only operations with 0 k requests and responses, 0 k requests and 4 k responses and 4 k requests and 0 k responses. � Overhead due to extra communication and encryption. �

Performance Evaluation: Replication Overhead � Comparison between BFS and BFS-nr, which is BFS that is not replicated. � � strict BFS - follows NFS semantics r/o lookup BFS – NFS lookup operation modified to be read-only to evaluate the read-only optimization.

Performance Evaluation: Direct Comparison � Comparison between BFS and the NFS V 2 implementation for Digital Unix. BFS only 3% slower than non-Byzantine Fault-Tolerant implementation! � Drawback: requires 3 f+1 replicas to ensure reliability. �