Builtin Adaptive Test and Calibration of DAC Wei

Built-in Adaptive Test and Calibration of DAC Wei Jiang and Vishwani D. Agrawal Electrical and Computer Engineering Auburn University, Auburn, AL 36849 18 th IEEE North Atlantic Test Workshop 2009

Outline • • • Overview Previous Work Proposed BIST Scheme Adaptive Self-Calibration of DAC Simulation Results Conclusion NATW'09 2

Overview • Proposed design-for-testability (DFT) architecture for a mixed-signal So. C – Accuracy – Performance – Cost • Test of on-chip DAC and ADC – Linearity (DNL/INL) – Resolution and speed – Signal-to-noise ratio (SNR) NATW'09 3

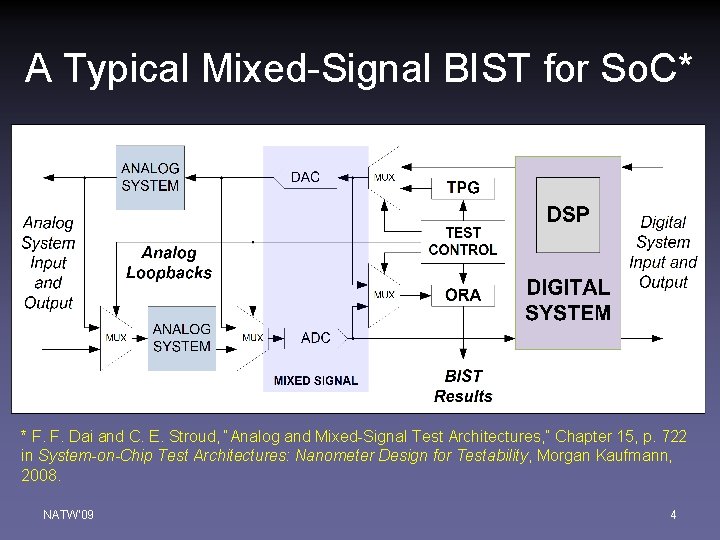
A Typical Mixed-Signal BIST for So. C* * F. F. Dai and C. E. Stroud, “Analog and Mixed-Signal Test Architectures, ” Chapter 15, p. 722 in System-on-Chip Test Architectures: Nanometer Design for Testability, Morgan Kaufmann, 2008. NATW'09 4

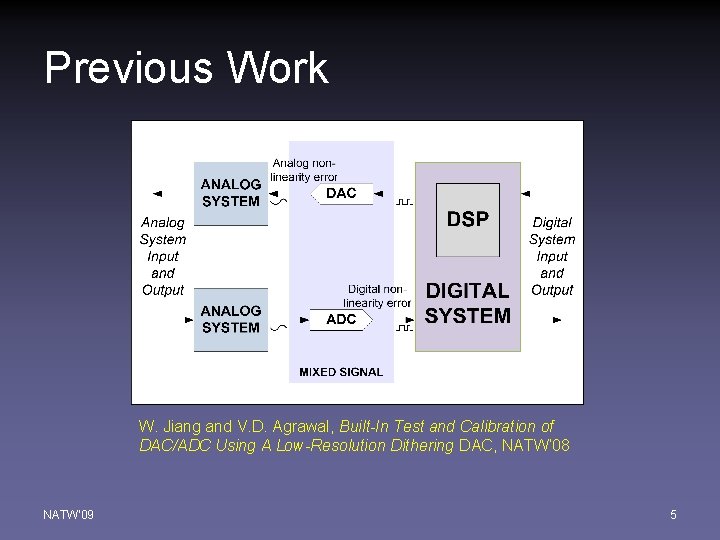
Previous Work W. Jiang and V. D. Agrawal, Built-In Test and Calibration of DAC/ADC Using A Low-Resolution Dithering DAC, NATW’ 08 NATW'09 5

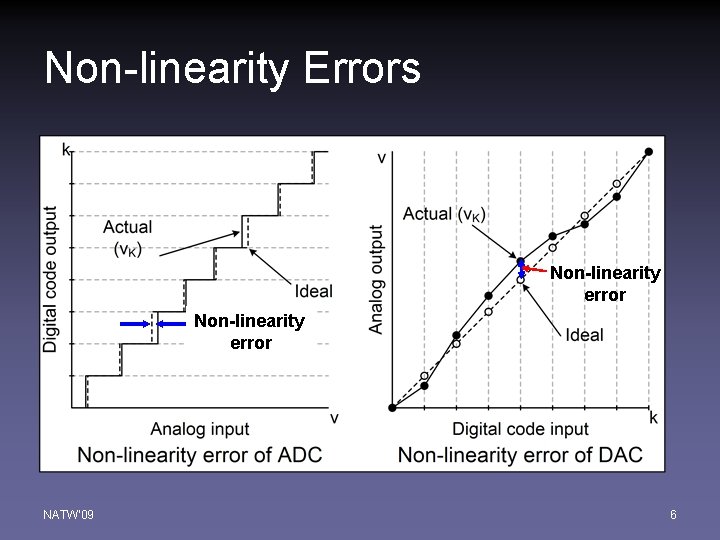
Non-linearity Errors Non-linearity error NATW'09 6

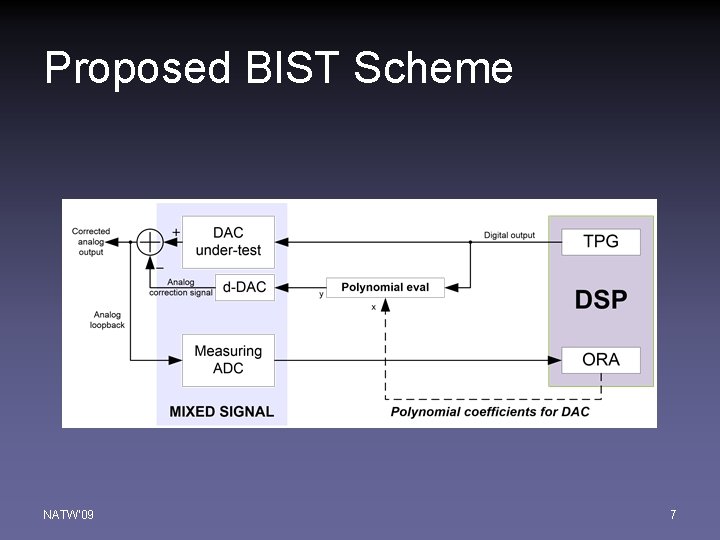
Proposed BIST Scheme NATW'09 7

Proposed BIST Scheme (Cont. ) • DSP for BIST control • Components – 1 -bit first-order sigma-delta modulator – Low-pass filter (integrator or comb filter) – Adaptive polynomial evaluation/fix circuit – Low-resolution dithering DAC – Loop-back circuitry connecting internal DAC and ADC NATW'09 8

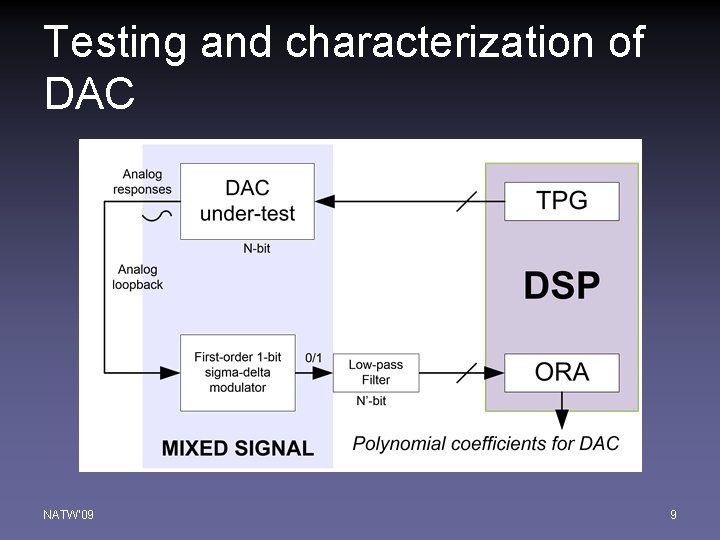
Testing and characterization of DAC NATW'09 9

Testing of DAC (Cont. ) • Response and ramp input compared for INL error • INL error analyzed by adaptive polynomial fitting algorithm • Best matching polynomials selected for various and DAC profiles • Test results indicated by calculated characteristics (offset, gain and harmonic distortion, etc) • Polynomial coefficients calculated for dithering DAC to improve INL NATW'09 10

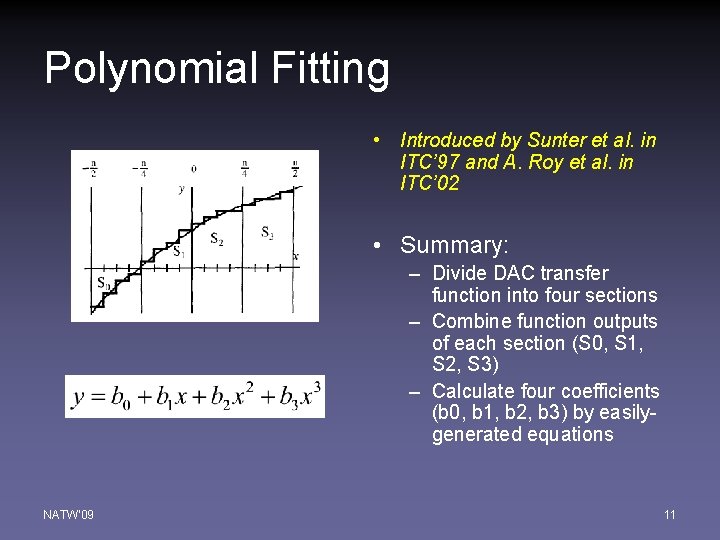
Polynomial Fitting • Introduced by Sunter et al. in ITC’ 97 and A. Roy et al. in ITC’ 02 • Summary: – Divide DAC transfer function into four sections – Combine function outputs of each section (S 0, S 1, S 2, S 3) – Calculate four coefficients (b 0, b 1, b 2, b 3) by easilygenerated equations NATW'09 11

Third-Order Polynomial NATW'09 12

First- and second-order Polynomial First-order polynomial Second-order polynomial NATW'09 13

Adaptive Polynomial Fitting • Fitting INL error from lower order polynomial to higher order • Calculate RMS error of each polynomial • Select the polynomial with least RMS error (when RMS error rising with higher order polynomial) NATW'09 14

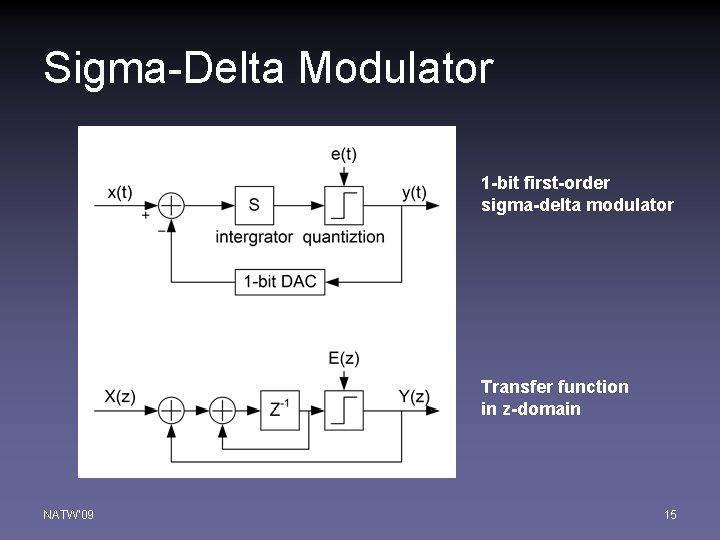
Sigma-Delta Modulator 1 -bit first-order sigma-delta modulator Transfer function in z-domain NATW'09 15

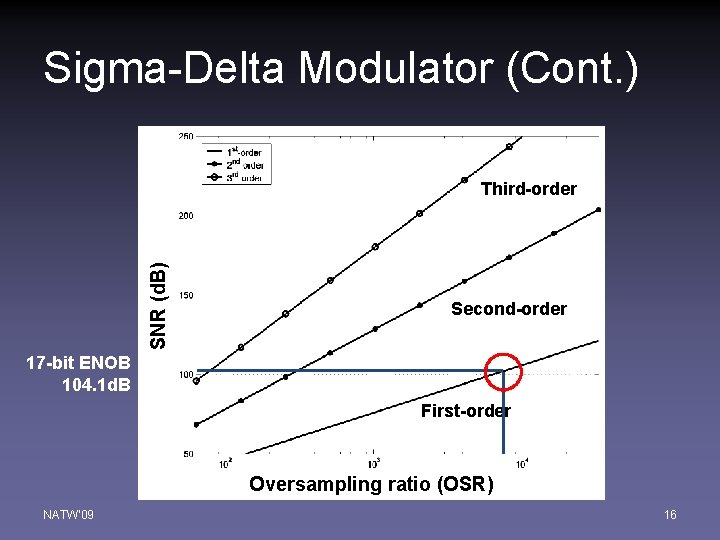
Sigma-Delta Modulator (Cont. ) SNR (d. B) Third-order Second-order 17 -bit ENOB 104. 1 d. B First-order Oversampling ratio (OSR) NATW'09 16

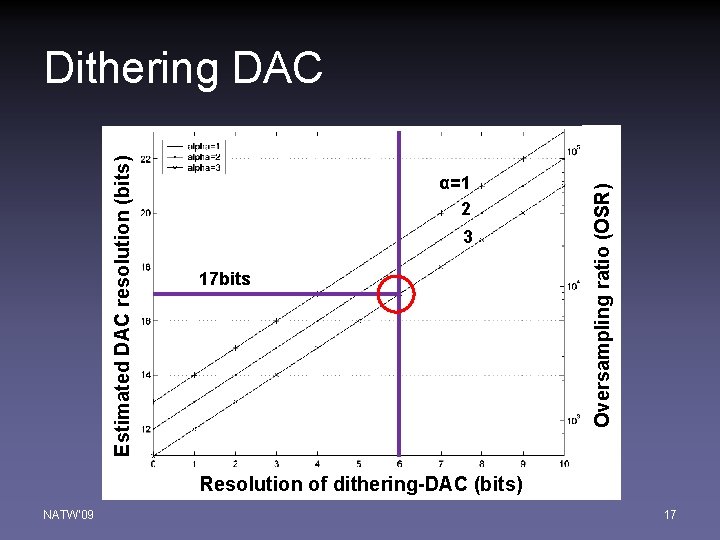
α=1 2 3 17 bits Oversampling ratio (OSR) Estimated DAC resolution (bits) Dithering DAC Resolution of dithering-DAC (bits) NATW'09 17

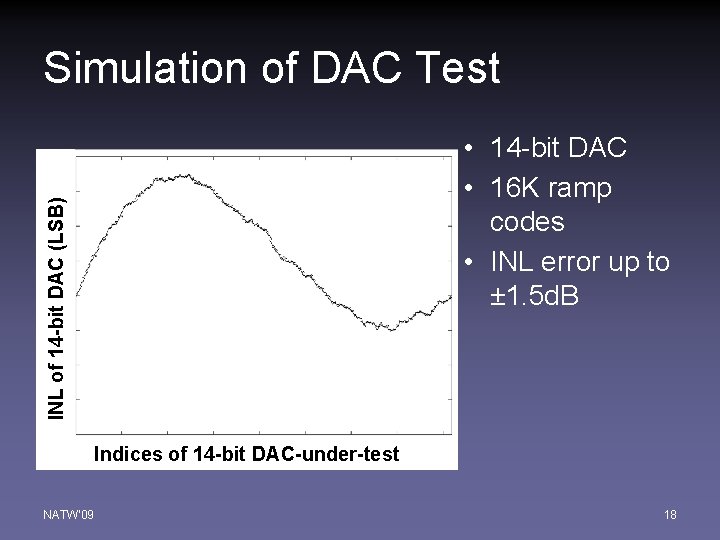
Simulation of DAC Test INL of 14 -bit DAC (LSB) • 14 -bit DAC • 16 K ramp codes • INL error up to ± 1. 5 d. B Indices of 14 -bit DAC-under-test NATW'09 18

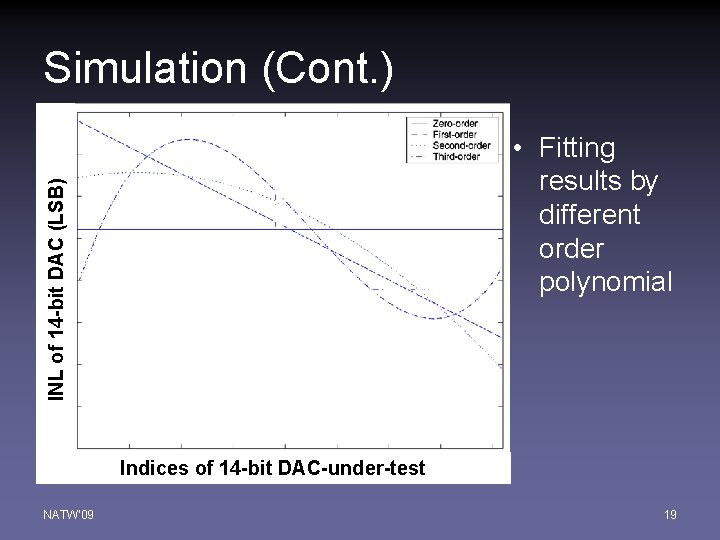
Simulation (Cont. ) INL of 14 -bit DAC (LSB) • Fitting results by different order polynomial Indices of 14 -bit DAC-under-test NATW'09 19

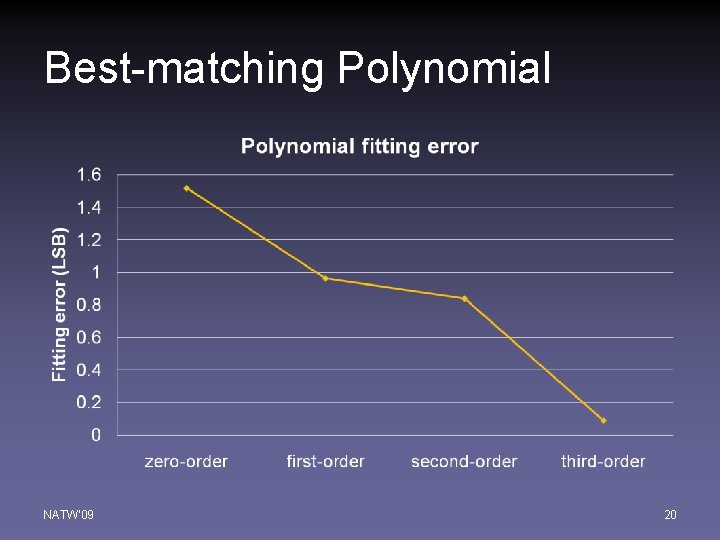
Best-matching Polynomial NATW'09 20

Conclusion • A built-in self-test and self-calibration solution for mixed-signal So. C is proposed • A polynomial fitting algorithm is employed for INL error correction • Fault-tolerance levels can be chosen for various applications • Simulation results show significant improvement in linearity after calibration NATW'09 21

Q&A Thank you! NATW'09 22