Building Java Programs Chapter 13 Searching and Sorting

Building Java Programs Chapter 13 Searching and Sorting Copyright (c) Pearson 2013. All rights reserved.

Sequential search 2

Sequential search • sequential search: Locates a target value in an array/list by examining each element from start to finish. – How many elements will it need to examine? – Example: Searching the array below for the value 42: index 0 1 value -4 2 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 7 10 15 20 22 25 30 36 42 50 56 68 85 92 103 i – Notice that the array is sorted. Could we take advantage of this? 3

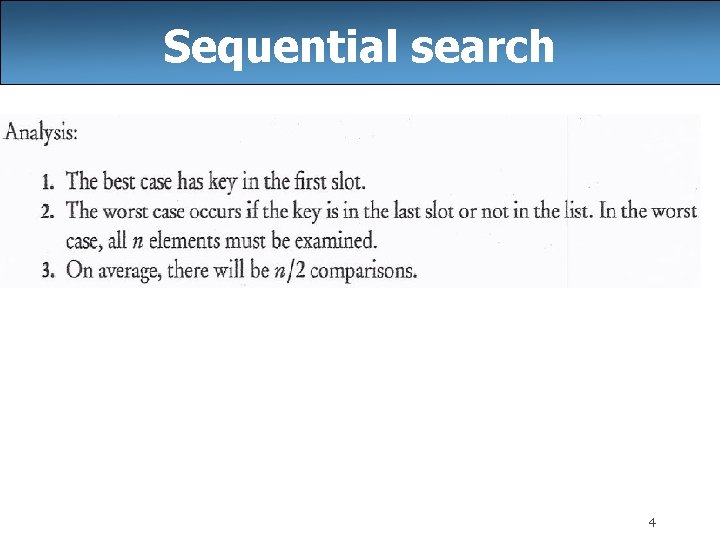
Sequential search 4

Binary search 5

Binary search 6

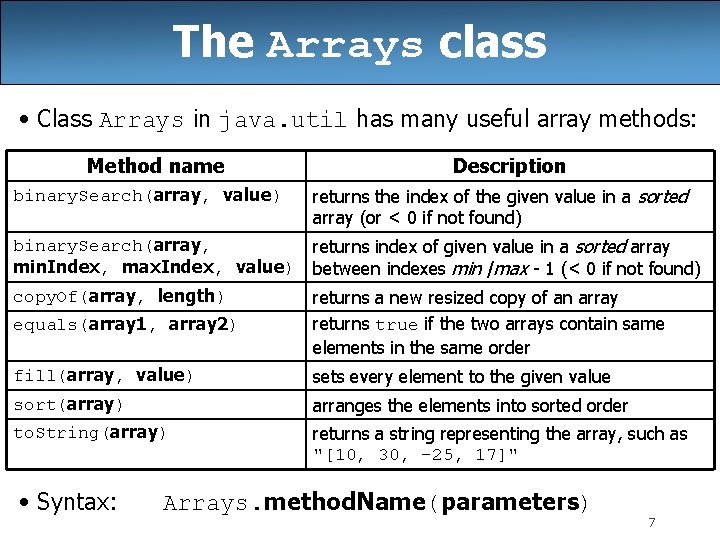
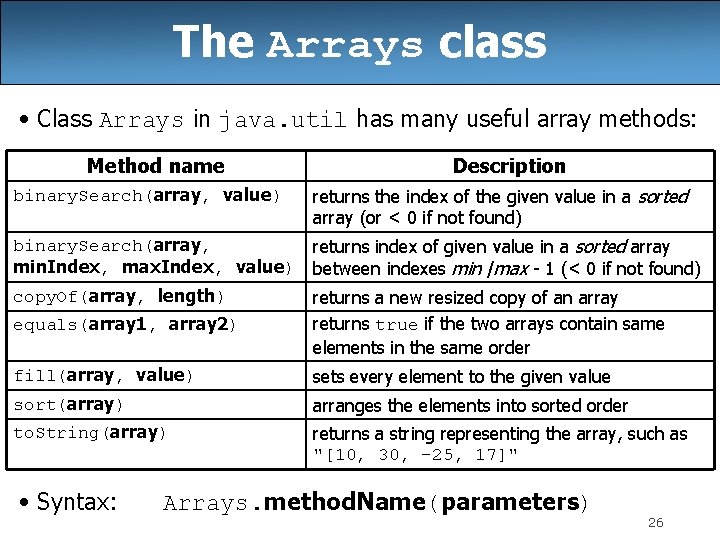
The Arrays class • Class Arrays in java. util has many useful array methods: Method name binary. Search(array, value) Description returns the index of the given value in a sorted array (or < 0 if not found) binary. Search(array, returns index of given value in a sorted array min. Index, max. Index, value) between indexes min /max - 1 (< 0 if not found) copy. Of(array, length) returns a new resized copy of an array equals(array 1, array 2) returns true if the two arrays contain same elements in the same order fill(array, value) sets every element to the given value sort(array) arranges the elements into sorted order to. String(array) returns a string representing the array, such as "[10, 30, -25, 17]" • Syntax: Arrays. method. Name(parameters) 7

Arrays. binary. Search // searches an entire sorted array for a given value // returns its index if found; a negative number if not found // Precondition: array is sorted Arrays. binary. Search(array, value) // // searches given portion of a sorted array for a given value examines min. Index (inclusive) through max. Index (exclusive) returns its index if found; a negative number if not found Precondition: array is sorted Arrays. binary. Search(array, min. Index, max. Index, value) • The binary. Search method in the Arrays class searches an array very efficiently if the array is sorted. – You can search the entire array, or just a range of indexes – If the array is not sorted, you may need to sort it first 8

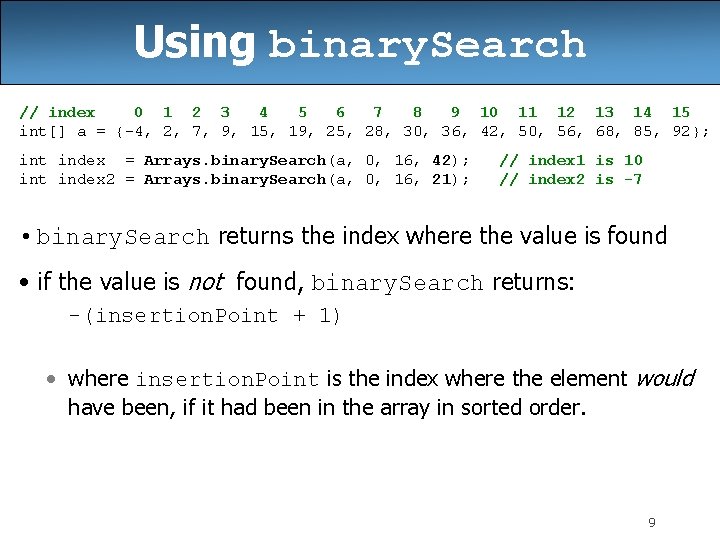
Using binary. Search // index 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 int[] a = {-4, 2, 7, 9, 15, 19, 25, 28, 30, 36, 42, 50, 56, 68, 85, 92}; int index = Arrays. binary. Search(a, 0, 16, 42); int index 2 = Arrays. binary. Search(a, 0, 16, 21); // index 1 is 10 // index 2 is -7 • binary. Search returns the index where the value is found • if the value is not found, binary. Search returns: -(insertion. Point + 1) • where insertion. Point is the index where the element would have been, if it had been in the array in sorted order. 9

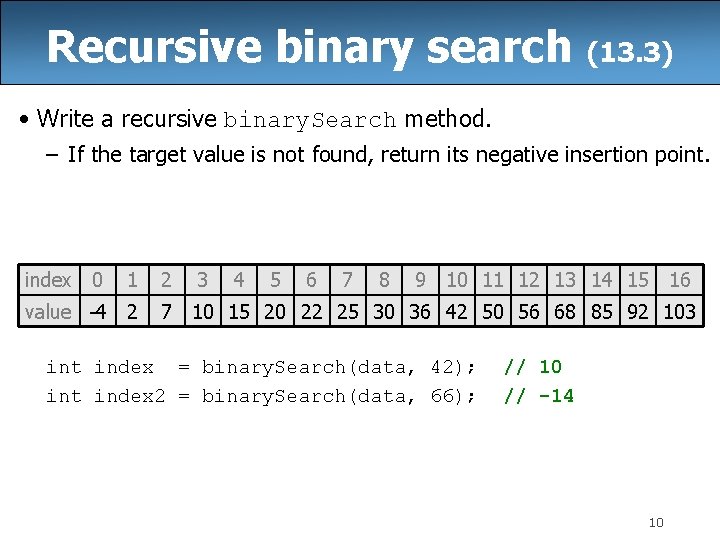
Recursive binary search (13. 3) • Write a recursive binary. Search method. – If the target value is not found, return its negative insertion point. index 0 1 value -4 2 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 7 10 15 20 22 25 30 36 42 50 56 68 85 92 103 int index = binary. Search(data, 42); int index 2 = binary. Search(data, 66); // 10 // -14 10

Binary search code // Returns the index of an occurrence of target in a, // or a negative number if the target is not found. // Precondition: elements of a are in sorted order public static int binary. Search(int[] a, int target) { int min = 0; int max = a. length - 1; while (min <= max) { int mid = (min + max) / 2; if (a[mid] < target) { min = mid + 1; } else if (a[mid] > target) { max = mid - 1; } else { return mid; // target found } } } return -(min + 1); // target not found 11

Binary search code using Recursion // Returns the index of an occurrence of the given value in // the given array, or a negative number if not found. // Precondition: elements of a are in sorted order public static int binary. Search(int[] a, int target) { return binary. Search(a, target, 0, a. length - 1); } // Recursive helper to implement search behavior. private static int binary. Search(int[] a, int target, int min, int max) { if (min > max) { return -1; // target not found } else { int mid = (min + max) / 2; if (a[mid] < target) { // too small; go right return binary. Search(a, target, mid + 1, max); } else if (a[mid] > target) { // too large; go left return binary. Search(a, target, min, mid - 1); } else { return mid; // target found; a[mid] == target } } } 12

Binary search 13

Runtime Efficiency (13. 2) • efficiency: A measure of the use of computing resources by code. – can be relative to speed (time), memory (space), etc. – most commonly refers to run time • Assume the following: – Any single Java statement takes the same amount of time to run. – A method call's runtime is measured by the total of the statements inside the method's body. – A loop's runtime, if the loop repeats N times, is N times the runtime of the statements in its body. 14

Efficiency examples statement 1; statement 2; statement 3; 3 for (int i = 1; i <= N; i++) { statement 4; } N for (int i = 1; i <= N; i++) { statement 5; statement 6; statement 7; } 3 N 4 N + 3 We say that this method runs 4 N + 3 Statements 15

Efficiency examples 2 for (int i = 1; i <= N; i++) { for (int j = 1; j <= N; j++) { statement 1; } } N 2 for (int i = 1; i <= N; i++) { N 2 + 4 N statement 2; 4 N statement 3; statement 4; statement 5; } • How many statements will execute if N = 10? If N = 1000? We say that this method runs N 2 + 4 N Statements 16

Algorithm growth rates (13. 2) • We measure runtime in proportion to the input data size, N. – growth rate: Change in runtime as N changes. • Say an algorithm runs 0. 4 N 3 + 25 N 2 + 8 N + 17 statements. – Consider the runtime when N is extremely large. – We ignore constants like 25 because they are tiny next to N. – The highest-order term (N 3) dominates the overall runtime. – We say that this algorithm runs "on the order of" N 3. – or O(N 3) for short ("Big-Oh of N cubed") 17

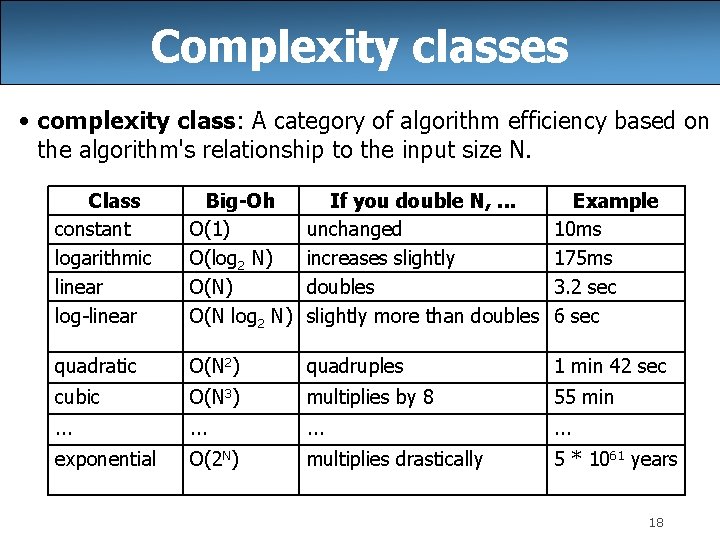
Complexity classes • complexity class: A category of algorithm efficiency based on the algorithm's relationship to the input size N. Class constant logarithmic linear log-linear Big-Oh O(1) O(log 2 N) O(N log 2 N) If you double N, . . . unchanged increases slightly doubles slightly more than doubles Example 10 ms 175 ms 3. 2 sec 6 sec quadratic O(N 2) quadruples 1 min 42 sec cubic O(N 3) multiplies by 8 55 min . . . exponential O(2 N) multiplies drastically 5 * 1061 years 18

Range algorithm What complexity class is this algorithm? Can it be improved? // returns the range of values in the given array; // the difference between elements furthest apart // example: range({17, 29, 11, 4, 20, 8}) is 25 public static int range(int[] numbers) { int max. Diff = 0; // look at each pair of values for (int i = 0; i < numbers. length; i++) { for (int j = 0; j < numbers. length; j++) { int diff = Math. abs(numbers[j] – numbers[i]); if (diff > max. Diff) { max. Diff = diff; } } } return diff; } 19

Range algorithm 2 The algorithm is O(N 2). A slightly better version: // returns the range of values in the given array; // the difference between elements furthest apart // example: range({17, 29, 11, 4, 20, 8}) is 25 public static int range(int[] numbers) { int max. Diff = 0; // look at each pair of values for (int i = 0; i < numbers. length; i++) { for (int j = i + 1; j < numbers. length; j++) { int diff = Math. abs(numbers[j] – numbers[i]); if (diff > max. Diff) { max. Diff = diff; } } } return diff; } 20

Range algorithm 3 This final version is O(N). It runs MUCH faster: // returns the range of values in the given array; // example: range({17, 29, 11, 4, 20, 8}) is 25 public static int range(int[] numbers) { int max = numbers[0]; // find max/min values int min = max; for (int i = 1; i < numbers. length; i++) { if (numbers[i] < min) { min = numbers[i]; } if (numbers[i] > max) { max = numbers[i]; } } return max - min; } 21

Runtime of first 2 versions • Version 1: • Version 2: 22

Runtime of 3 rd version • Version 3: 23

Sorting • sorting: Rearranging the values in an array or collection into a specific order (usually into their "natural ordering"). – one of the fundamental problems in computer science – can be solved in many ways: • there are many sorting algorithms • some are faster/slower than others • some use more/less memory than others • some work better with specific kinds of data • some can utilize multiple computers / processors, . . . – comparison-based sorting : determining order by comparing pairs of elements: • <, >, compare. To, … 24

Sorting methods in Java • The Arrays and Collections classes in java. util have a static method sort that sorts the elements of an array/list String[] words = {"foo", "bar", "baz", "ball"}; Arrays. sort(words); System. out. println(Arrays. to. String(words)); // [ball, bar, baz, foo] List<String> words 2 = new Array. List<String>(); for (String word : words) { words 2. add(word); } Collections. sort(words 2); System. out. println(words 2); // [ball, bar, baz, foo] 25

The Arrays class • Class Arrays in java. util has many useful array methods: Method name binary. Search(array, value) Description returns the index of the given value in a sorted array (or < 0 if not found) binary. Search(array, returns index of given value in a sorted array min. Index, max. Index, value) between indexes min /max - 1 (< 0 if not found) copy. Of(array, length) returns a new resized copy of an array equals(array 1, array 2) returns true if the two arrays contain same elements in the same order fill(array, value) sets every element to the given value sort(array) arranges the elements into sorted order to. String(array) returns a string representing the array, such as "[10, 30, -25, 17]" • Syntax: Arrays. method. Name(parameters) 26

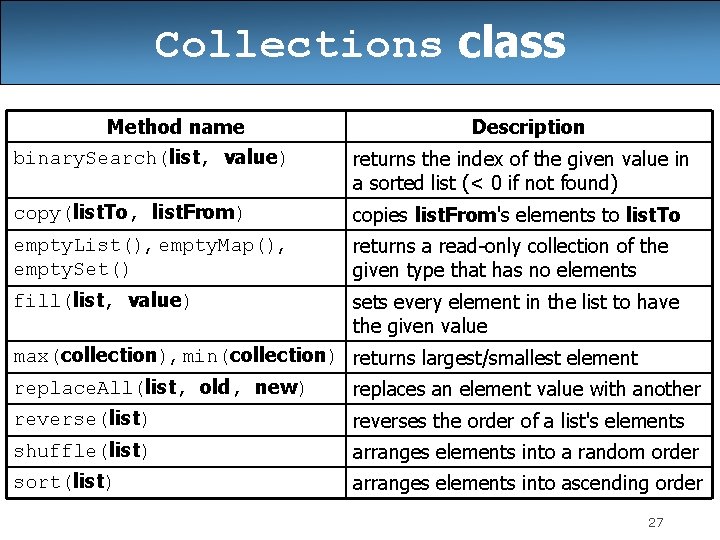
Collections class Method name binary. Search(list, value) Description returns the index of the given value in a sorted list (< 0 if not found) copy(list. To, list. From) copies list. From's elements to list. To empty. List(), empty. Map(), empty. Set() returns a read-only collection of the given type that has no elements fill(list, value) sets every element in the list to have the given value max(collection), min(collection) returns largest/smallest element replace. All(list, old, new) replaces an element value with another reverse(list) reverses the order of a list's elements shuffle(list) arranges elements into a random order sort(list) arranges elements into ascending order 27

Sorting algorithms • • bogo sort: shuffle and pray bubble sort: swap adjacent pairs that are out of order selection sort: look for the smallest element, move to front insertion sort: build an increasingly large sorted front portion merge sort: recursively divide the array in half and sort it heap sort: place the values into a sorted tree structure quick sort: recursively partition array based on a middle value other specialized sorting algorithms: • bucket sort: cluster elements into smaller groups, sort them • radix sort: sort integers by last digit, then 2 nd to last, then. . . • . . . 28

Sorting algorithms for AP Exam • • Selection Sort Insertion Sort Merge Sort: Quick Sort: 29

Selection sort • selection sort: Orders a list of values by repeatedly putting the smallest or largest unplaced value into its final position. The algorithm: – Look through the list to find the smallest value. – Swap it so that it is at index 0. – Look through the list to find the second-smallest value. – Swap it so that it is at index 1. . – Repeat until all values are in their proper places. 30

Selection sort 31

Selection sort 32

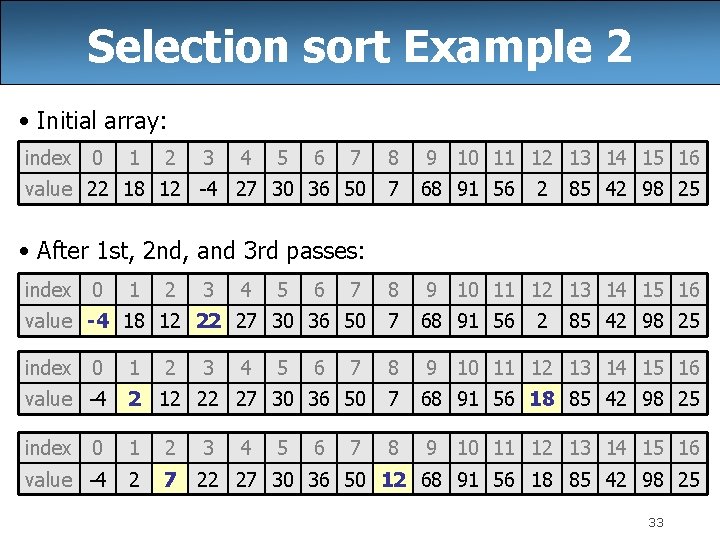
Selection sort Example 2 • Initial array: index 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 value 22 18 12 -4 27 30 36 50 7 68 91 56 7 8 9 10 11 12 13 14 15 16 value -4 18 12 22 27 30 36 50 7 68 91 56 index 0 1 7 8 9 10 11 12 13 14 15 16 value -4 2 12 22 27 30 36 50 7 68 91 56 18 85 42 98 25 index 0 1 2 3 8 9 10 11 12 13 14 15 16 value -4 2 7 22 27 30 36 50 12 68 91 56 18 85 42 98 25 2 85 42 98 25 • After 1 st, 2 nd, and 3 rd passes: index 0 1 2 2 3 3 4 4 4 5 5 5 6 6 6 7 2 85 42 98 25 33

Selection sort code // Rearranges the elements of a into sorted order using // the selection sort algorithm. public static void selection. Sort(int[] a) { for (int i = 0; i < a. length - 1; i++) { // find index of smallest remaining value int min = i; for (int j = i + 1; j < a. length; j++) { if (a[j] < a[min]) { min = j; } } // swap smallest value its proper place, a[i] swap(a, i, min); 34

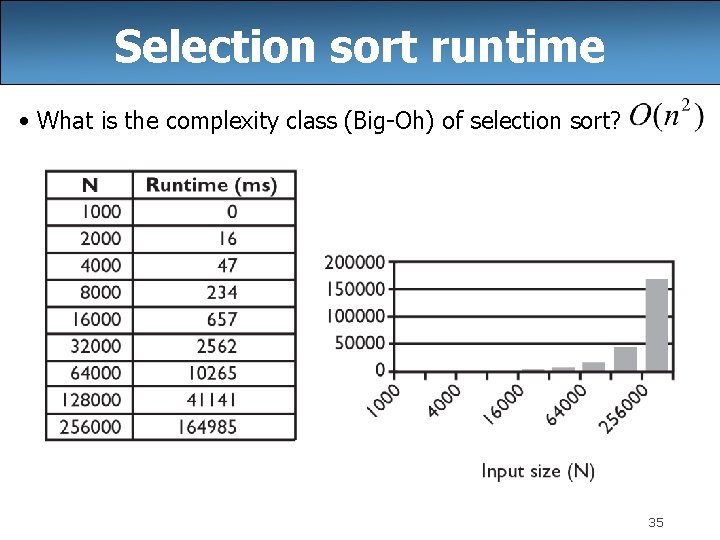
Selection sort runtime • What is the complexity class (Big-Oh) of selection sort? 35

Insertion sort 36

Insertion sort 37

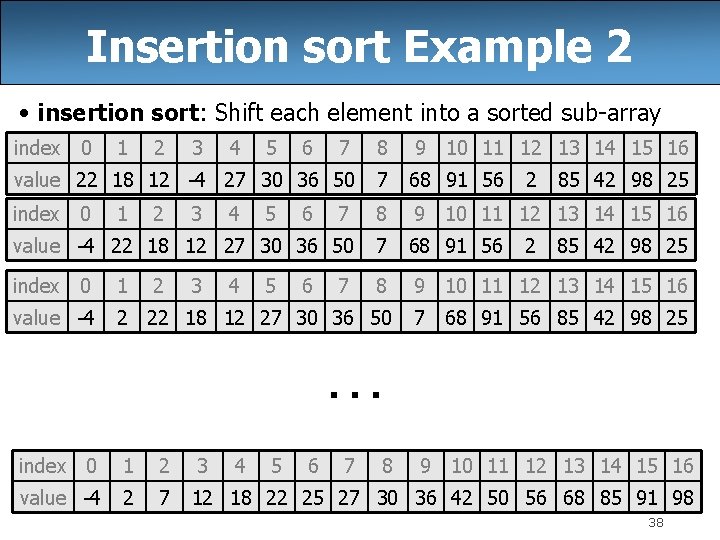
Insertion sort Example 2 • insertion sort: Shift each element into a sorted sub-array index 0 1 7 8 9 10 11 12 13 14 15 16 value 22 18 12 -4 27 30 36 50 7 68 91 56 index 0 7 8 9 10 11 12 13 14 15 16 value -4 22 18 12 27 30 36 50 7 68 91 56 index 0 1 8 9 10 11 12 13 14 15 16 value -4 2 22 18 12 27 30 36 50 7 68 91 56 85 42 98 25 1 2 2 2 3 3 3 4 4 4 5 5 5 6 6 6 7 2 2 85 42 98 25 … index 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 value -4 2 7 12 18 22 25 27 30 36 42 50 56 68 85 91 98 38

Selection and Insertion sort 39

Merge sort • merge sort: Repeatedly divides the data in half, sorts each half, and combines the sorted halves into a sorted whole. The algorithm: – Divide the list into two roughly equal halves. – Sort the left half. – Sort the right half. – Merge the two sorted halves into one sorted list. – Often implemented recursively. – An example of a "divide and conquer" algorithm. • Invented by John von Neumann in 1945 40

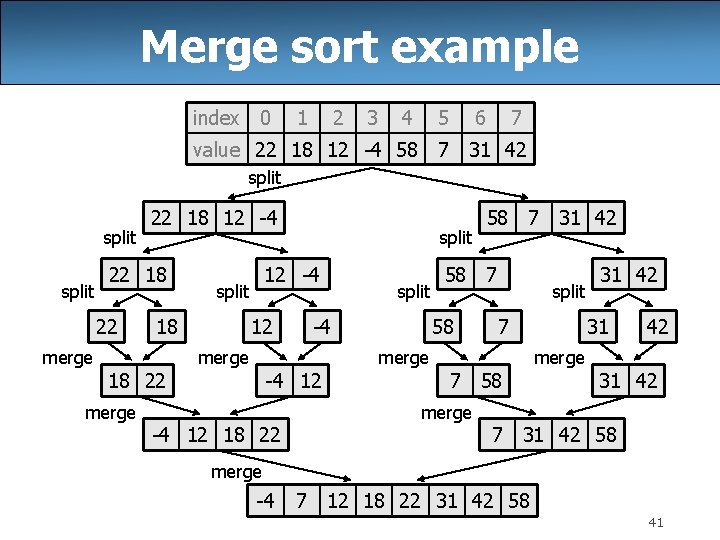
Merge sort example index 0 1 2 3 4 5 6 7 value 22 18 12 -4 58 7 31 42 split 22 18 12 -4 22 18 22 merge 12 -4 split 18 split 12 split -4 merge 58 7 31 42 58 7 58 split 7 merge 18 22 -4 12 merge 31 42 merge 7 58 31 42 merge -4 12 18 22 7 31 42 58 merge -4 7 12 18 22 31 42 58 41

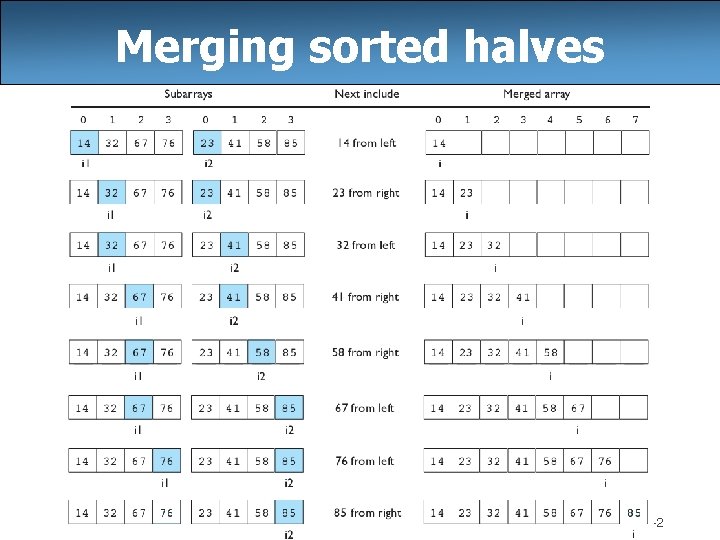
Merging sorted halves 42

Merge halves code // Merges the left/right elements into a sorted result. // Precondition: left/right are sorted public static void merge(int[] result, int[] left, int[] right) { int i 1 = 0; // index into left array int i 2 = 0; // index into right array for (int i = 0; i < result. length; i++) { if (i 2 >= right. length || (i 1 < left. length && left[i 1] <= right[i 2])) { result[i] = left[i 1]; // take from left i 1++; } else { result[i] = right[i 2]; // take from right i 2++; } } } 43

Merge sort code // Rearranges the elements of a into sorted order using // the merge sort algorithm (recursive). public static void merge. Sort(int[] a) { if (a. length >= 2) { // split array into two halves int[] left = Arrays. copy. Of. Range(a, 0, a. length/2); int[] right = Arrays. copy. Of. Range(a, a. length/2, a. length); // sort the two halves merge. Sort(left); merge. Sort(right); // merge the sorted halves into a sorted whole merge(a, left, right); } } 44

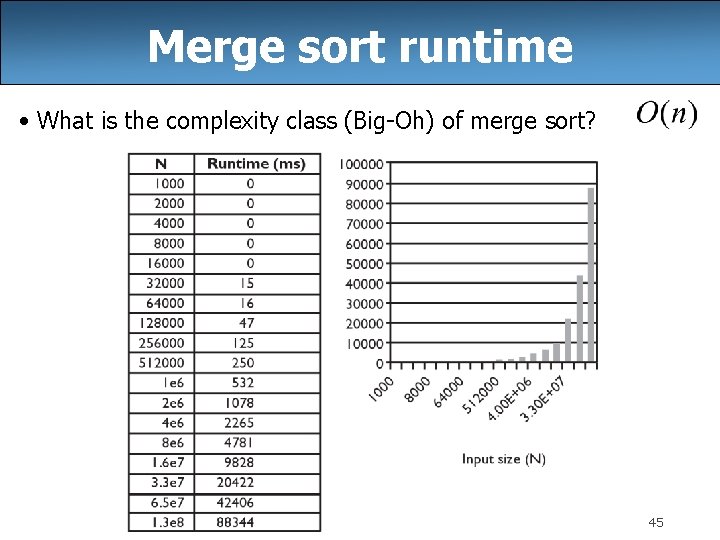
Merge sort runtime • What is the complexity class (Big-Oh) of merge sort? 45

Analysis of Mergesort Part 1 46

Analysis of Mergesort Part 2 47

Analysis of Mergesort Part 3 Another example of Mergesort 48

Analysis of Mergesort Part 4 49

Quicksort 50

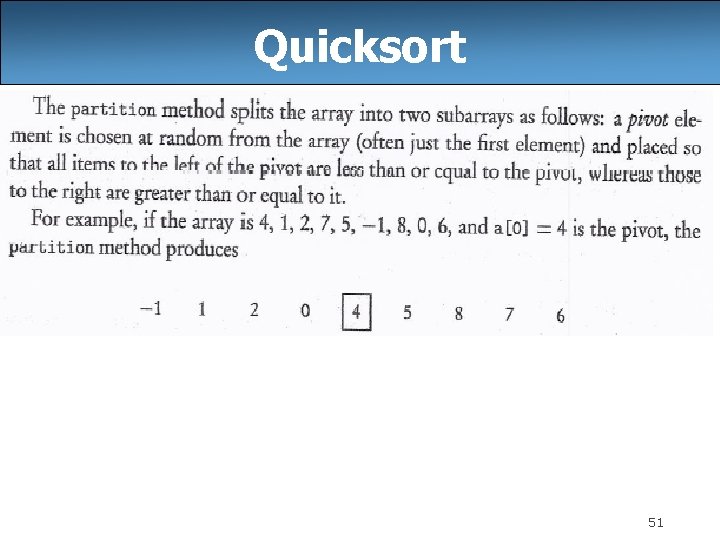
Quicksort 51

Quicksort 52

Analysis of Quicksort 53

Analysis of Quicksort 54

Searching and Sorting in Java’s Class Libraries 55

Custom ordering with Comparators 56

Custom ordering with Comparators What if we wanted to order the strings in a case-insensitive comparison. We might also want an option to sort in other orders, such as by length or in reverse alphabetical order. 57

Custom ordering with Comparators 58

Comparator: Example 1 59

Comparator: Example 2 60

Comparator: Example 2 61

Comparator: Example 3 Note: This slide is referring to the Point class of the Java class library, not the one we wrote in class. 62

Comparator: Example 3 63

Comparator: Example 3 64

Comparators and Methods 65